2. 中国科学院网络化控制系统重点实验室, 辽宁 沈阳 110016;
3. 中国科学院大学, 北京 100049
2. Key Laboratory of Networked Control Systems, Chinese Academy of Sciences, Shenyang 110016, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
1 引言
无线传感器网络(wireless sensor network，WSN)[1, 2]是由大量具有计算和通信能力的微型传感器节点组成的无线自组织网络，由于其低成本、低功耗特性，已经广泛应用于工业、农业、环境监测等领域. 当前，WSN的通信频段以免申请的ISM 2.4 GHz频段为主. 仅以工业应用[3]为例，国际标准WirelessHART、WIA-PA和ISA 100.11a均以IEEE 802.15.4物理层为基础，至少采用它在2.4 GHz频段定义的15个信道作为通信信道. 此外，已经广泛应用的ZigBee、BlueTooth、Wi-Fi等短距离无线通信技术也都工作在这一频段，因此造成了该频段的过度使用. 当不同网络部署于同一区域时，将不可避免地出现信道拥挤和相互干扰现象，严重降低通信的可靠性.
为了解决由于传统的静态频谱划分造成的频谱利用率低和信道拥挤问题，认知无线电(cognitive radio，CR)[4, 5]技术应运而生. 认知无线电通过动态频谱接入策略实现了频谱共享，提高了授权频段的频谱利用率. 但是，当前对于认知无线电的研究主要集中于电视、移动通信等授权频段，对于拥挤的ISM频段的认知技术研究较少. 实际上，将认知无线电的频谱感知技术应用于传感器网络，用以提高WSN在ISM频段通信的可靠性是一个可行方案. 随着WSN和CR技术的相继成熟，关于认知无线传感器网络(cognitive wireless sensor networks，CWSN)[6]的研究已经悄然兴起，并成为WSN和CR这一交叉领域的新兴研究热点. CWSN是一种具有频谱感知能力的WSN，可以根据它的认知结果动态调整设备的运行参数，实现网络的可靠传输. 然而，目前对于CWSN的网络架构并没有统一的定义. 现有的研究工作，如文[6, 7, 8, 9]，主要采用认知无线网络(cognitive radio network，CRN)的基本架构，并应用动态频谱接入的策略，而对于WSN所固有的低成本、低功耗等特点考虑甚少. 实际上，应该从CWSN所采用认知方法的适用性以及硬件的可实现性等方面综合考虑，真正实现面向应用的CWSN.
因此，本文提出了一种全新的CWSN架构. 该架构在不改变WSN既有特性的基础上，通过在网络中部署专门负责频谱感知的认知节点，实现了CWSN的可靠传输. 由于将频谱感知与数据传输功能进行了合理地划分，所以无需全网节点增加感知时隙和感知设备，有效增大了网络吞吐量，降低了设备成本和网络能耗. 此外，在认知节点间实现了一种优化的协作频谱感知(cooperative spectrum sensing，CSS)[5]策略. 该策略以最大化网络吞吐量为目标，对协作感知的决策融合准则和认知节点数量进行了优化. 基于这一优化策略，可以在满足信道检测率要求的前提下，在每个信道上以最小的能耗获得最大的网络吞吐量.
2 认知无线传感器网络模型新的认知无线传感器网络架构充分考虑WSN的既有特性，以WSN为基本模型，在网络中增加了具有频谱感知能力的认知节点. 其基本模型如图 1所示，主要包括汇聚节点、传感节点和认知节点三类节点.
 |
| 图 1 认知无线传感器网络示意Fig. 1 Schematic diagram of CWSN |
认知节点是专门负责频谱感知的节点，可以对本地ISM频段的多信道进行联合检测[10]，并将局部感知结果上报给汇聚节点. 多个认知节点协作进行频谱感知，可以有效避免多径衰落、隐藏终端、阴影和遮蔽等影响，提高感知的准确性. 认知节点的部署密度可以根据网络的可靠性需求进行灵活调整，一般小于传感节点的部署密度. 汇聚节点是网络的协调器和融合中心，负责整个网络的建立、组织和管理. 既要对传感节点的采集数据进行汇聚、处理和存储，也要对认知节点报告的局部感知结果进行融合，实现对多信道状态的全局判别. 这样，当全局判决结果显示当前信道已被占用或不适合继续通信时，汇聚节点可以从全局判决序列中选择一个状况良好的信道. 然后通过广播方式与传感节点和认知节点共同切换到该可靠信道，实现网络的自适应信道切换.
由于CRN需要接入授权频段，所以为了充分保护授权用户，CRN采用的是动态频谱接入策略. 因此，CRN的全部节点均要具有频谱感知能力，并且需要在每个帧中单独划定感知时隙[11, 12]. 如图 2所示，一个帧长度为Tall，包含的感知时隙长度为T. 根据该帧结构，网络节点首先进行频谱感知，然后根据感知结果选择是否进行数据传输. 但是，这种结构并不适合工作于ISM频段的传感器网络，它不仅缩短了数据传输时间，降低了网络吞吐量，而且增大了设备成本和网络能耗. 而本文所提出的CWSN架构中，通过专门的认知节点进行多信道感知，并不需要全网节点增加感知模块和感知时隙. 因此可以降低网络设备成本和缩短数据传输周期，同时增大网络吞吐量. 当然，传感节点采集的物理信息和认知节点感知的信道信息在CWSN中的传输调度以及网络的自适应信道切换都是通过MAC层协议完成的，这里不做详细讨论.
 |
| 图 2 具有感知时隙CRN帧结构Fig. 2 CRN frame structure with sensing slot |
CWSN中认知节点进行本地感知所采用的方法是多信道联合检测，即对ISM 2.4 GHz的M个带宽为W的信道同时进行独立感知. 这样，认知节点在每个信道m(m=1，…，M)上的频谱感知问题可以通过二元假设检验进行描述，原假设H0，m代表信道m未被占用，备择假设H1，m代表信道m已被占用，其基本形式如下：
基于上述假设检验模型，可以对每个信道进行频谱感知. 目前，CR技术所提供频谱感知算法主要包括能量检测、匹配滤波、循环平稳特征检测、特征值检测等[13]. 但是，无论是从算法的复杂度，还是从硬件的可实现角度来说，目前真正适用于CWSN的方法只有能量检测算法. 能量检测具有实现简单、计算复杂度低、无需信号先验知识等特点，特别适用于低成本、低功耗的CWSN. 因此，多信道联合检测采用能量感知算法.
认知节点的多信道联合检测原理如图 3所示，其过程如下： 认知节点首先对在有限时间T内接收到的信号通过带通滤波器进行噪声预滤波，然后经过A/D转换、串并转换得到每个信道上的S个采样值. 各信道上的采样值经平方、求和及均值后，进入比较器进行阈值判决. 这样，避免了传统模拟采样过程中的波形重建过程，而仅对每个信道上的S个采样值进行能量检测即可.
 |
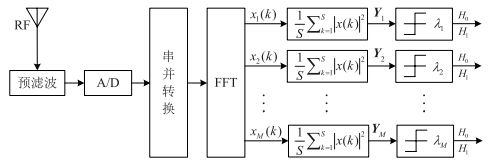| 图 3 多信道联合检测原理Fig. 3 Principle of multi-channel joint detection |
认知节点对单个信道m的能量检测结果Ym=
服从自由度为S=2u的卡方分布. u=TW表示时间带宽积，通常为整数. 进而可以得到反映单个认知节点检测可靠性的3个指标(虚警率P(m)f、检测率P(m)d和漏警率P(m)m)的解析表达式[14].
P(m)f表示信道m未被占用时，认知节点判定该信道被占用的虚警概率；Pd(m)表示正确检测到信道m已被占用的概率；而Pm(m)表示信道m已被占用时，仍判定信道状态良好的漏警概率. 对于CWSN来说，应该尽可能提高P(m)d以增强信道检测的可靠性，同时减小P(m)f以提高信道的利用率. 但是两者之间存在一个动态平衡，很难同时实现. 因此，通常采用恒虚警率或恒检测率的方法加以实现. (1)式和(2)式表明在给定u的情况下，P(m)f仅由λ决定，而P(m)d和P(m)m则由λ和反映信道状况的信噪比γ共同决定. 这样，单个认知节点对M个信道的联合检测概率可以表示为Pd=[Pd(1)，Pd(2)，…，Pd(M)].
3.2 认知节点的协作感知信号的传输过程中不可避免地会遇到多径衰落、遮蔽、隐藏终端等问题，而协作频谱感知通过探索频谱的空间分集特性，可以有效地解决上述问题[5, 15, 16]. CSS可以采用数据融合或决策融合的方法对本地感知结果进行处理. 对于CRN来说，数据融合是一种理想方案，可以采用等增益合并(EGC)、最大比率合并(MRC)、选择合并(SC)等方法[17]. 但是数据融合需要传输频谱感知的原始数据，对带宽和吞吐量的要求比较高，即网络开销大，因此并不适合传感器网络. 而采用决策融合只需认知节点发送1 bit的局部判决结果到汇聚节点即可，这就大大减少了数据传输和网络能耗，因此这里采用决策融合. 此外，由于CWSN具有短距离传输特性，故各认知节点到汇聚节点所经过的信道衰落都相同，满足γ1=…=γN=γ.
假设CWSN中有N个认知节点参与协作感知，Ym(n)表示认知节点n对信道m的能量检测结果，则N个认知节点对M个信道的检测结果可用如下矩阵表示.
决策融合时，单个认知节点n对M个独立信道分别进行本地判决：
汇聚节点对N个认知节点的本地判决结果进行全局融合
. 这样，汇聚节点将得到协作的认知节点对M个独立信道的全局融合结果
根据该结果，汇聚节点进行全局判决. 其中，当Dallm≥K时，判定信道m被占用；当Dmall<K时，判定信道m未被占用. 该判别准则称为“K-out-of-N”准则[5]，即当有K个认知节点判别信道m被占用时，认为该信道确被占用. 特别地，当K=1时称为OR准则，K=N时称为AND准则，而K=「N/2]时称为Majority准则，「·]表示向上取整. 其中，OR准则为大多数CRN所采用. 此时，N个认知节点对信道m进行协作感知所得的虚警率Qf(m)、检测率Qd(m)和漏警率Qm(m)分别如下：
由于本文所提出的CWSN架构中部署有专门负责频谱感知的认知节点，所以仅有认知节点分配感知时隙进行频谱感知，而不需要全网节点分配感知时隙. 相应地，网络中的传感节点可以使用帧的全部时隙进行数据传输，因此可以有效提升整个网络的吞吐量. 为此，这里对网络的吞吐量进行详细的比较，并提出一种优化的协作感知策略进一步提升网络吞吐量.
根据香农定理，信道容量的计算式可以表示为C=W·lb(1+SNR). 其中，SNR为信噪比应用到基于CSS的CWSN中，以信道m为例，存在如下两种情况： 1) 信道m状况良好且协作感知的判决结果正确，则吞吐量为R0(m)=
信道m质量不佳，但协作感知出错，判定信道质量良好，此时的吞吐量为
假设信道质量好与差的概率分别为P0和P1，则信道m的平均吞吐量为
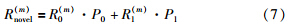
相应地，传统网络架构下的吞吐量可以根据图 2所示的帧结构计算如下[11, 12]：
显然，信道m的吞吐量与该信道的容量C以及认知节点的协作感知结果Qf(m)和Qd(m)有关. 更进一步说，它是关于信噪比γ、时间带宽积u、能量检测阈值λ以及决策融合阈值K和认知节点数量N的函数. 因此，这里以最大化网络吞吐量为目标，建立如下优化问题：
由于上述问题中的K和N均为正整数，要得到它的解析解十分困难，所以本文采用二维搜索的方法求解. 当网络节点总数Nall给定时，由于参与协作的认知节点数N不得大于Nall，并且决策融合阈值K也不得大于认知节点数N，所以进行二维搜索的复杂度并不高. 这样，通过二维搜索可以获得信道m的最大吞吐量以及决策融合阈值K和最优节点数量N. 这里将求解优化问题(10)获得的最优解(K，N)所形成的决策融合准则称为最优R准则.
为了比较网络架构的差异，进一步考虑在传统架构下采用通用的OR准则和文[15]的优化准则所获得的网络吞吐量. 其中，在OR准则下，K=1. 而文[15]证明了在满足总错误率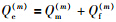
最小的情况下，求解最优决策融合阈值K的计算式：
，其中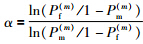
. 这里，将文[15]所给出的最优决策准则称为最优K准则.
图 4给出了在本文架构下采用最优R准则和在传统网络架构下采用OR准则和最优K准则所获得吞吐量曲线. 相关的仿真参数设置如下： 时间带宽积u=1，W=10 Hz，帧长度Tall=100 ms，能量检测阈值λ=10，信道状态假设为P0=0.8和P1=0.2. 此外，两种架构下网络节点总数均为Nall=50. 其中传统架构下要求Nall个节点全部参与感知和传输，然后分别应用OR和最优K准则进行决策融合. 而在本文架构下，尽管部署有Nall个节点，由于采用了最优R准则，并不需要全部参与感知.
 |
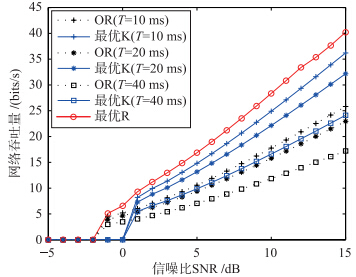| 图 4 不同网络架构下的吞吐量Fig. 4 Throughput under different network architectures |
通过图 4可以看出，当信噪比很低时，采用三种融合准则所获得的吞吐量差别不大，这是因为能量检测在低信噪比条件下的感知性能有限. 但是，随着信噪比的增大，网络吞吐量差异迅速增大. 其中，在传统架构下采用通用OR准则的网络吞吐量最低. 相比之下，同一架构下采用最优K准则的吞吐量获得了大幅提升. 但是，与新架构下所采用的最优R准则相比，吞吐量还有一定差距. 特别是当网络的信噪比低时，最优R准则仍可以获得少量的吞吐量增益，说明其抗噪声性能要好于最优K准则. 此外，从网络的架构上分析，传统网络架构下的网络吞吐量均随感知时隙的增大而减小. 这一问题正是传统网络架构所固有的感知时隙与传输时隙的折中问题[11, 12]. 而本文所提出的新架构由于将感知与传输功能进行了合理地分配，故并不存在上述折衷问题.
图 5给出了CWSN网络规模对吞吐量的影响. 由于低信噪比条件下的网络吞吐量差异不大，故这里仅给出信噪比大于5 dB的吞吐量比较. 假设传统网络的感知时间为T=10 ms. 可以看到，通用OR准则在N增大的情况下，吞吐量是下降的. 这是因为网络节点数越多，节点达成完全一致的概率也就越低，即对各信道的检测越严格. 这种策略提高了信道的检测率，但是降低了网络的吞吐量. 而在传统架构下采用最优K准则和在本文架构下采用最优R准则，在满足信道检测率Q(m)f>0.9的情况下，可以获得更高的吞吐量. 并且，当信噪比增大时，包含不同数量节点的网络的吞吐量可以达到一致. 但是，相比之下，在新的网络架构下采用最优R准则获得的吞吐量更大.
 |
| 图 5 不同网络规模下的吞吐量Fig. 5 Throughput under different network scales |
通过上面的讨论可以看出，参与协作感知的认知节点数量并不是越多越好. 不同规模的CWSN所获得的吞吐量，在信噪比高的情况下会趋于一致. 因此，过多的认知节点将会增大网络的成本和能耗. 特别是对于低功耗的CWSN来说，降低不必要的认知能耗更具意义. 因此，这里对新架构下的网络能耗与传统网络做以比较.
假设网络的节点总数为Nall不变. 通过求解优化问题(10)，可以获得参与协作感知的最优认知节点数N. 在新的网络架构下，频谱感知功能和数据传输功能分别由认知节点和传感节点完成. 所以，进一步假设网络可以通过汇聚节点的配置使得其余Nall-N个节点作为传感节点进行数据传输. 做出这一假设的目的是让两种网络架构下的节点总数相同，确保网络能耗比较的公平性.
对于新的网络架构而言，网络的总能耗为
. 其中，认知节点的感知能耗Es等于参与协作感知的认知节点数量N与单位节点的感知能耗es之积，即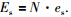
而传感节点进行数据传输的能耗为
其中et为传输单位比特数据的能耗，
为单位帧时间内传输的数据总量. 而在传统架构下，由于全网节点都要进行频谱感知和数据传输，所以根据图 2所示的帧结构，网络总能耗为
其中
作为比较，这里考虑文[15]所进一步给出的求解最优节点数量Nopt的优化准则，称之为最优N准则，并将其应用在新的网络架构下. 最优N准则的主要思想是通过将总错误率Qe(m)构造为协作节点数量n和融合阈值k的函数
然后，通过求解下面的优化问题获得参与协作感知的最优节点数量.
图 6给出了在传统架构下采用OR准则以及在新架构下采用最优N准则和最优R准则的网络能耗比较. 其中，单位节点的感知能耗为190 nJ，传输单位比特数据的能耗为150 nJ/bit[18]. 感知时隙长度为T=10 ms，Nall=50，其余参数设置与前面相同. 根据已经获得的吞吐量，并假设网络节点以该最大速率进行数据传输，可以分别计算两种网络架构下单位时间内传输的数据量，进而可以计算网络能耗.
 |
| 图 6 不同网络架构下的能耗Fig. 6 Energy consumption under different network architectures |
图 6表明，在传统网络架构下，网络能耗随信噪比的增大而增大，这是因为信道质量好的情况下，传输的数据量大，导致总能耗增大. 但是由于传统架构下的全部网络节点均要进行频谱感知，故它的网络能耗要大于新的网络架构. 具体来说，在满足信道检测率要求的前提下，新的网络架构并不需要全网节点参与感知，因此减少了大量不必要的感知能耗，并相应地增加了传输能耗. 但是，相比于最优N准则，最优R准则在信噪比大于6 dB以后的能耗更低. 而在信噪比低的情况下，两者的差别并不大. 此外，最优R准则的能耗并不是线性变化的，存在一定波动，这是因为在满足信道检测率要求的前提下，为了获得最大网络吞吐量，参与感知的认知节点数量不是线性变化的. 但是，从能耗来看，在新网络架构下采用最优R准则要好于最优N准则以及传统架构下的OR准则.
5 结论本文提出了一种新的CWSN架构，将频谱感知和数据传输功能进行了合理地划分. 首先由认知节点进行本地的多信道联合检测，然后多个认知节点协作进行频谱感知. 网络中的传感节点根据协作感知的决策融合结果选择最佳的信道进行数据传输. 同时，以最大化吞吐量为目标，优化了协作感知的决策融合准则和协作节点数量. 在提高检测率的同时，降低了网络能耗. 结果表明，优化后的CSS可以有效提高CWSN的可靠性和吞吐量，降低CWSN的成本和功耗. 未来，基于CSS的CWSN可以应用于WIA-PA等高可靠、强实时性的工业无线网络.
| [1] | Akyildiz I F, Su W, Sankarasubramaniam Y, et al. A survey on sensor networks[J]. IEEE Communication Magazine, 2002, 40(8): 102-114. |
| [2] | 于海斌, 梁炜, 曾鹏. 智能无线传感器网络系统[M]. 2版. 北京: 科学出版社, 2013. Yu H B, Liang W, Zeng P. Intelligent wireless sensor networks system[M]. 2nd ed. Beijing: Science Press, 2013. |
| [3] | 何之栋, 张伟宁, 王海凤, 等. 工业无线网络路由及调度联合极值优化[J]. 信息与控制, 2014, 43(2): 152-158. He Z D, Zang W N, Wang H F, et al. Joint routing and scheduling optimization in industrial wireless networks using an external dynamics algorithm[J]. Information and Control, 2014, 43(2): 152-158. |
| [4] | Wang B B, Ray Liu K J. Advances in cognitive radio networks: A survey[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(1): 5-23. |
| [5] | Akyildiz I F, Lo B F, Balakrishnan R. Cooperative spectrum sensing in cognitive radio networks: A survey[J]. Physical Communication, 2011, 4(1): 40-62. |
| [6] | Vijay G, Bdira E B A, Ibnkahla M. Cognition in wireless sensor networks: A perspective[J]. IEEE Sensor Journal, 2011, 11(3): 582-592. |
| [7] | Jamal A, Tham C K, Wong W C. Event detection and channel allocation in cognitive radio sensor networks[C]//IEEE International Conference on Communication Systems (ICCS). Piscataway, NJ, USA: IEEE, 2012: 157-161. |
| [8] | Deng R L, Chen J M, Yuen C, et al. Energy-efficient cooperative spectrum sensing by optimal scheduling in sensor-aided cognitive radio networks[J]. IEEE Transactions on Vehicular Technology, 2012, 61(2): 716-725. |
| [9] | Hareesh K, Poonam S. An energy efficient hybrid co-operative spectrum sensing technique for CRSN[C]//International Multi-Conference on Automation, Computing, Communication, Control and Compressed Sensing (iMac4s). Piscataway, NJ, USA: IEEE, 2013: 438-442. |
| [10] | Quan Z, Cui S, Sayed A H, et al. Optimal multiband joint detection for spectrum sensing in cognitive radio networks[J]. IEEE Transactions on Signal Processing, 2009, 57(3): 1128-1140. |
| [11] | Liang Y C, Zeng Y H, Peh E C Y, et al. Sensing-throughput tradeoff for cognitive radio networks[J]. IEEE Transactions on Wireless Communications, 2008, 7(4): 1326-1337. |
| [12] | Zeng Y H, Peh E C Y, Liang Y C, et al. Optimization of cooperative sensing in cognitive radio networks: A sensing-throughput tradeoff view[J]. IEEE Transactions on Vehicular Technology, 2009, 58(9): 5294-5299. |
| [13] | Yucek T, Arslan H. A survey of spectrum sensing algorithms for cognitive radio applications[J]. IEEE Communications Surveys & Tutorials, 2009, 11(1): 116-130. |
| [14] | Umar R, Sheikh U H A, Deriche M. Unveiling the hidden assumptions of energy detector based spectrum sensing for cognitive radios[J]. IEEE Communications Surveys & Tutorials, 2014, 16(2): 713-728. |
| [15] | Zhang W, Mallik K R, Letaief K B. Optimization of cooperative spectrum sensing with energy detection in cognitive radio networks[J]. IEEE Transactions on Wireless Communications, 2009, 8(12): 5761-5766. |
| [16] | Ghasemi A, Sousa S E. Opportunistic spectrum access in fading channels through collaborative sensing[J]. Journal of Communications, 2007, 2(2): 71-82. |
| [17] | Atapattu S, Tellambura C, Jiang H. Performance of an energy detector over channels with both multipath fading and shadowing[J]. IEEE Transactions on Wireless Communications, 2010, 9(12): 3662-3670. |
| [18] | Maleki S, Pandharipande A, Leus G. Energy-efficient distributed spectrum sensing for cognitive sensor networks[J]. IEEE Sensor Journal, 2011, 11(3): 565-573. |