2. 沈阳建筑大学信息与控制工程学院, 辽宁 沈阳 110168;
3. 中国科学院沈阳自动化研究所, 辽宁 沈阳 110016
2. School of Information and Control Engineering, Shenyang Jianzhu University, Shenyang 110168, China;
3. Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang 110016, China
1 引言
大型建筑结构的安全不仅关系到社会经济的命脉,还影响着经济生产和人民生活,结构健康监测(structural health monitoring,SHM)已成为国际社会研究的前沿课题[1]. 结构健康监测是通过一系列传感器定时获取建筑物的动力和静力响应测量值,从中抽取损伤敏感特征因子,并进行统计分析,进而获得当前结构健康状况的过程,其中结构故障检测是SHM系统的主要任务之一[2].
模拟生物免疫机理的克隆选择算法,由于具有学习、 记忆、 进化等特点,使其在异物检测、 网络入侵检测、 模式识别、 故障诊断和医学图像处理等领域得到广泛应用,非常适用于结构健康监测[3, 4, 5, 6, 7, 8, 9, 10]. 近年来,经过研究者的不断努力,免疫算法在故障诊断中取得了一些成果:2007年,湖南大学的于德介等提出了基于人工免疫机制的结构损伤检测方法,讨论了相关参数对损伤及其位置识别的影响,并以上海东海大桥船碰桥墩监测数据分析为例证明了所提方法的有效性[11];2009年,Chen等人受到生物免疫系统启发,针对结构健康监测,研究了具有自治、 自适应、 主动监测的类似生物免疫系统的人工免疫算法,并在Benchmark结构模型上验证了基于传感器网络的人工免疫算法的有效性[12];2012年,Mojtahedi等利用改进的人工免疫算法检测近海岸平台故障[13]. 但单纯应用克隆选择算法也存在一些不足[14, 15]:一是,由于算法采用二进制编码,每次计算抗体亲和力时都必须对抗体进行解码,计算量增加,同时二进制的位数也限制了求解的精度;二是,变异是通过随机改变原有克隆抗体的特征向量进行的,该过程在增加抗体多样性的同时也可能破坏亲和力高的抗体,从而增加了计算量;三是,每一代经抗原刺激进化产生的亲和力最高的抗体,不一定能被保存.
克隆选择算法中的变异操作是产生有潜力新抗体的唯一途径,因此必须保证克隆选择算法有较高的变异概率. 粒子群优化(particle swarm optimization,PSO)算法具有收敛速度快、 运算简单、 易于实现、 无编码和解码等复杂运算特点[16, 17]. 本文提出了一种基于粒子群优化变异的克隆选择算法,即将粒子群优化算法引入到克隆选择过程的变异环节中,不仅保证了变异后的抗体具有更高的亲和力,而且使变异不再依赖于二进制编码,大大减少了计算量.
2 结构故障检测与分类算法传感器采集的动态响应测量数据经过标准化、 降维和提取敏感损伤特征向量处理后,将通过本文提出的故障检测与分类算法来判断结构的故障模式. 此算法分为两个过程:
(1) 学习过程,即将样本结构模式(正常和故障)数据作为抗原,刺激抗体集合,抗体集合经过克隆、 粒子群优化变异、 选择等学习过程生成能够识别入侵抗原的记忆细胞集合.
(2) 应用过程,即应用学习后的记忆细胞集合对实测数据进行识别与分类,来判断该数据所属的结构模式.
2.1 学习过程本文中的初始抗体均是从每种故障模式的样本数据中随机选择形成的,初始记忆细胞集合是应用k均值算法产生的[18]. 学习过程又包括抗体集合进化和记忆细胞更新两个部分,图 1为学习过程示意图.
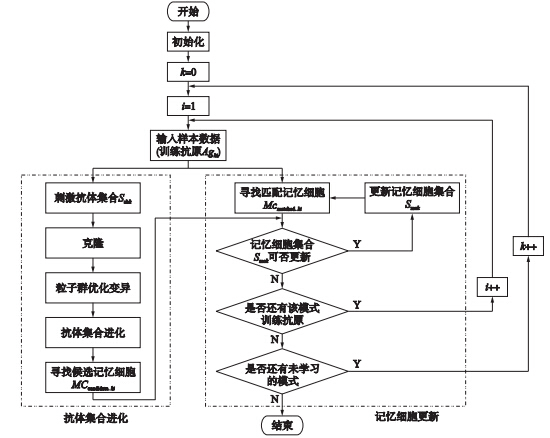 |
| 图 1 学习过程示意图Fig. 1 The schematic diagram of learning process |
本文符号表示如下:
ψ={0,1,…,k}表示k+1种结构模式的集合,即k∈ψ,且k=0为正常模式;
Agki表示第k种抗原集合Sagk中的第i个抗原,i={1,2,…,NAGk},其中NAGk为第k种模式抗原集合Sagk的规模,即
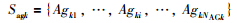
Abkj表示第k种抗体集合Sabk中的第j个抗体,j={1,2,…,NABk},其中NABk为第k种模式抗体集合Sabk的规模,即
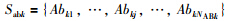
Mckl表示第k种记忆细胞集合Smck中第l个记忆细胞,l={1,2,…,NMCk},其中NMCk为第k种模式记忆细胞集合Smck的规模,即
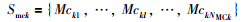
(1) 亲和力计算. 亲和力是指抗体与抗原的匹配程度. 第k种模式的抗原刺激该种模式的抗体集合,即抗原Agki作用于抗体集合Sabk中的每个抗体Abkj、 Agki和Abkj之间的亲和力aff(Agki,Abkj)为
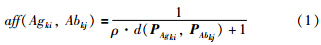
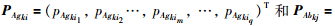
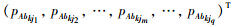 分别为
Agki和Abkj的特征向量;q为传感器采集的动态响应测量数据经标准化、 降维和提取敏感损伤特征向量处理后的数据维数;
分别为
Agki和Abkj的特征向量;q为传感器采集的动态响应测量数据经标准化、 降维和提取敏感损伤特征向量处理后的数据维数;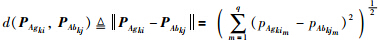 为
Agki和Abkj特征向量之间的欧氏距离,ρ代表亲和力系数,ρ∈(0,1]. 由式(1)可见,两个特征向量之间的距离决定了亲和力的大小,距离越大,亲和力越小;反之,亲和力越大.
为
Agki和Abkj特征向量之间的欧氏距离,ρ代表亲和力系数,ρ∈(0,1]. 由式(1)可见,两个特征向量之间的距离决定了亲和力的大小,距离越大,亲和力越小;反之,亲和力越大. (2) 克隆. 根据生物免疫学原理,亲和力越大,抗体克隆的次数就越多. 假设抗体集合Sabk中的Abkj被克隆数目为Mkj,则Mkj由克隆率ω(ω≥1)和亲和力值共同决定,为
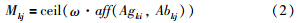
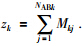 克隆不会改变抗体的特征向量.
克隆不会改变抗体的特征向量. (3) 粒子群优化变异. 为了增加抗体的多样性,克隆后的抗体要经历一个体细胞变异的过程. 粒子群算法将每个个体视为q维搜索空间中的一个无体积无质量的粒子,在搜索空间中以某速度飞行,并根据对个体和群体的飞行经验的综合分析来动态调整该速度,然后通过迭代来寻找最优解. 本文在变异过程中引用粒子群优化算法,增加抗体多样性的同时,避免了高亲和力抗体被破坏,保证了抗体向优化方向更新.
将抗体集合S′abk中的每个抗体Abko看作一个粒子,其中o={1,2,…,zk},每个粒子的初始速度vko(0)随机产生,则每个粒子速度vko的特征向量为Pvko=(pvko1,pvko2,…,pvkoq)T. 抗原Agki与抗体Abko之间亲和力越大,表示该抗体位置越好. 本文令每次变异操作,粒子群优化迭代的次数为N. 第k种模式每个粒子Abko至第t代为止搜索到的粒子最优位置记为popt-Abko(t),则 ,其中t={1,2,…,N}代表更新迭代次数. 第k种模式的整个粒子群至第N代为止搜索到的粒子群最优位置为popt-Abkg(t),则
,其中t={1,2,…,N}代表更新迭代次数. 第k种模式的整个粒子群至第N代为止搜索到的粒子群最优位置为popt-Abkg(t),则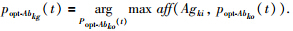 . 整个粒子群根据popt-Abko(t)和popt-Abkg(t)更新自身的速度vko和位置Abko,至T=N为止,实现粒子群优化变异,过程描述为
. 整个粒子群根据popt-Abko(t)和popt-Abkg(t)更新自身的速度vko和位置Abko,至T=N为止,实现粒子群优化变异,过程描述为
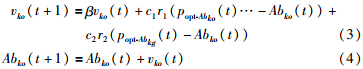
(4) 选择和进化. 根据抗体与抗原之间亲和力aff(Agki,Abkv)大小,其中Abkv∈(Sabk∪S″abk),将集合Sabk和S′abk中的抗体降序排列,选出前NABk个抗体作为新一轮的更新进化抗体集合Sabk,其余的抗体舍弃,保持抗体规模不变,仍为NABk.
定义1 候选记忆细胞Mccandidate. ki,为进化后的抗体集合Sabk中与给定抗原Agki有最高亲和力的抗体,即:

定义2 候选距离rms(Mccandidate. ki,Smck),为候选记忆细胞Mccandidate. ki与同种模式记忆细胞集Smck之间的均方根距离,其中rms(Mccandidate. ki,Smck)为
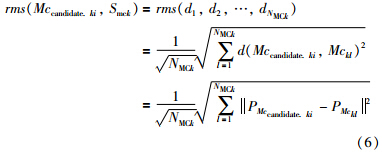
可见,rms(Mccandidate. ki,Smck)值越大意味着Mccandidate. ki和Smck之间的距离越大,Mccandidate. ki和Smck中的记忆细胞之间的差异越大.
定义3 匹配记忆细胞Mcmatched. ki为记忆细胞集合Smck中与抗原Agki亲和力最大的记忆细胞,即
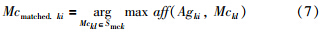
本文根据Mccandidate. ki、 rms(Mccandidate. ki,Smck)和Mcmatched. ki来进行记忆细胞集合的更新,具体规则如下:
(1) 如果(aff(Mccandidate. ki,Agki)∩aff(Mccandidate. ki,Mcmatched. ki))>ε,其中ε∈(0,1)为匹配记忆细胞替换阈值,则记忆细胞集合Smck中的匹配记忆细胞Mcmatched. ki将被候选记忆细胞Mccandidate. ki替换.
(2) 如果(rms(Mccandidate. ki,Smck)>τ)∪(aff(Mccandidate. ki,Agki)>aff(Mcmatched. ki,Agki))∩(aff(Mccandidate. ki,Mcmatched. ki)≤ε),其中τ∈(0,1)为候选记忆细胞替换阈值,则首先从相应的记忆细胞集合Smck中随机删除一个记忆细胞,然后将候选记忆细胞Mccandidate. ki加入到记忆细胞集合Smck中.
(3) 否则,记忆细胞集合Smck将不发生任何改变.
这样,通过该规则来寻找经抗原刺激进化产生的优秀抗体,并加入记忆细胞集合中.
2.2 应用过程假设所有的结构模式均通过学习过程形成了相应的记忆细胞集合,那么所有可能的模式(正常或故障)都能够被系统所识别. 在线应用过程就是利用学习训练过程产生的K+1个记忆细胞集合来判断实测数据所归属的模式,图 2所示为其应用过程示意图.
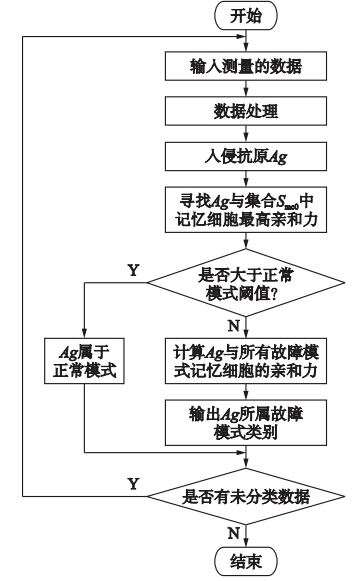 |
| 图 2 应用过程示意图Fig. 2 The schematic diagram of applying process |
一个模式未知的时间序列数据,经标准化、 降维和提取敏感损伤特征向量处理后视为入侵抗原Ag. 通过计算Ag与记忆细胞集合间的亲和力,判断输出模式的类别,具体为:
(1) 从k=0正常模式开始,若集合Smc0中的记忆细胞与Ag的最高亲和力大于θ,其中θ∈(0,1)为正常模式阈值,即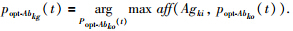 ,则测得的状态为正常模式;否则为故障模式,转(2).
,则测得的状态为正常模式;否则为故障模式,转(2).
(2) 计算Ag与所有故障模式记忆细胞的亲和力,与Ag有最高亲和力的记忆细胞所在的模式即为Ag所属故障模式km,即
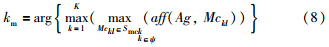
由IASC-ASCE SHM任务组提出的Benchmark结构[19]提供了5种模式实验数据,即k=4,包括正常模式(k=0)和4种故障模式,4种故障模式分别为:
(1) 去除第1层所有斜撑;
(2) 去除第1层和第3层所有斜撑;
(3) 去除第1层1根斜撑;
(4) 去除第1层和第3层各一根斜撑.
首先,本文针对每种模式采用300个样本数据进行训练该故障检测与分类系统;然后,通过应用在250种不同条件下产生的数据验证所提算法分类成功率. 分类成功率为
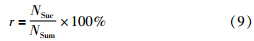
本节分析了克隆率ω、 匹配记忆细胞替换阈值ε和克隆选择算法迭代次数T对系统分类成功率r的影响,并与Chen使用的人工免疫算法[20]得到的分类成功率进行了对比分析.
3.2.1 克隆率ω与分类成功率r的关系取ε=0.99,T=100,θ=0.85,如图 3所示,两种算法的r开始都随着ω的增大而增高,而当ω继续增大时趋于稳定. 本文算法ω从1~6期间,r从69%上升到85%,上升比较快;当ω继续增大时,r基本保持85%不变,仍然比较高. 与Chen的人工免疫算法相比,本文算法不但在总体上分类成功率较高,而且在ω较小,即抗体克隆数目较少时,粒子群优化变异避免了高亲和力的抗体被破坏,保证了变异后的抗体拥有更高的亲和力,分类成功率明显高于Chen的人工免疫算法.
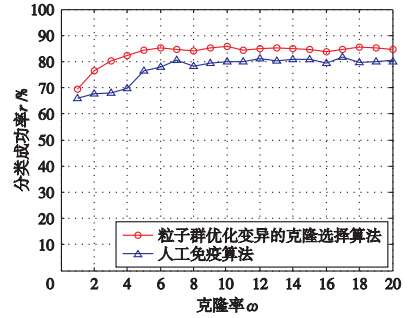 |
| 图 3 克隆率ω与分类成功率r关系Fig. 3 The relationship between clone rate ω and classification success rate r |
取ε=0.99,ω=10,θ=0.85,如图 4所示,两种算法中r均为开始随着迭代次数的增加而增高,而后保持稳定. 本文算法在第10~30代时,r从74%增加到85%,迭代次数继续增加,r基本不变. 与Chen的算法相比,本文算法分类成功率较高. 在每次迭代变异过程中,每个抗体粒子向临近的最优粒子进行移动,快速生成亲和力更高的抗体,加快了收敛速度,而Chen的算法由于变异方向的不确定性,迭代次数增加,运算缓慢. 结果表明,此算法提高r的同时,减少了迭代次数,提高了算法的收敛速度.
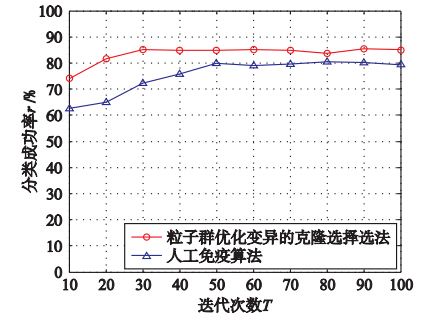 |
| 图 4 迭代次数与分类成功率r的关系Fig. 4 The relationship between the number of iterations and classification success rate r |
取ω=10,T=100,θ=0.85,如图 5所示,两种算法中r均随着ε的增大而增高,当ε接近1时r达到最高. 与Chen的算法相比本文算法中,当ε小于0.8时,分类成功率在60%左右,而当ε接近1时,分类成功率可达到85%,此时候选记忆细胞被注入到记忆细胞集合当中,但候选记忆细胞替换匹配记忆细胞的可能性很小,记忆细胞集合质量得以提高,从而提高了r. 粒子群优化变异使得抗体集合能向亲和力更高的方向进化,提高了r.
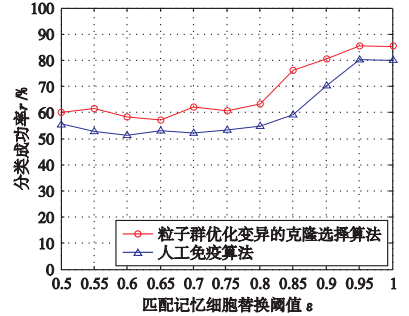 |
| 图 5 匹配记忆细胞替换阈值ε与分类成功率r关系Fig. 5 The relationship between matched memory cell replacement threshold ε and classification success rate r |
取ε=0.99,ω=10,T=100,如图 6所示,两种算法中r开始均随着θ的增大而增高,分类成功率达到最高后,随着θ的增大而减小. 与Chen的算法相比本文算法中,θ从0.55上升到0.85时,r从52%上升到85%,当θ继续增大到1时,r逐渐减小到70%左右,本文算法分类成功率能达到更高. θ较小时,入侵抗原与正常模式的记忆细胞集合之间亲和力较低即被判断为正常模式,此时,部分故障样本将被判断成正常模式;反之,θ较大时,入侵抗原与正常模式的记忆细胞集合之间亲和力较高才能被判断为正常模式,此时,部分正常样本将被判断成故障模式.
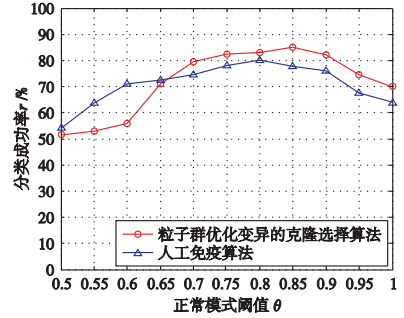 |
| 图 6 正常模式阈值θ与分类成功率r关系Fig. 6 The relationship between normal pattern threshold θ and classification success rate r |
本文针对大型建筑结构的故障检测与分类问题,提出了基于粒子群优化变异的克隆选择算法. 该方法一方面在变异过程中,引入粒子群优化算法,解决了原算法变异方向性不确定问题;另一方面定义了记忆细胞集合更新规则,使优秀抗体得以保存. 在Benchmark模型上验证了该算法的有效性. 与人工免疫算法相比,该方法收敛速度更快,显著提高了故障分类的成功率.
| [1] | Lynch J P. An overview of wireless structural health monitoring for civil structures[J]. Philos Transact A Math Phys Eng Sci, 2007, 365(1851): 345-372. |
| [2] | Worden K, Farrar C R, Manson G, et al. The fundamental axioms of structural health monitoring[J]. Physical and Engineering Sciences, 2007, 463(2082): 1639-1664. |
| [3] | 杨福刚, 孙同景, 宋松林. 基于人工免疫算法的药液颗粒异物检测方法[J]. 电子测量与仪器学报, 2008, 22(1): 20-23. Yang F G, Sun T J, Song S L. Artificial immune algorithm based particle detection method for liquid in pharmaceutical container[J]. Journal of Electronic Measurement and Instrument, 2008, 22(1): 20-23. |
| [4] | 陈晋音, 杨东勇. 基于轻量级人工免疫计算的混合入侵检测方法[J]. 信息与控制, 2012, 41(5): 529-536. Chen J Y, Yang D Y. Hybrid intrusion detection method based on light-weighted artificial immune computation[J]. Information and Control, 2012, 41(5): 529-536. |
| [5] | Deng J Y, Mao Z Y, Luo Y H. Pattern recognizing algorithm based on artificial immune network[J]. Journal of South China University of Technology: Natural Science, 2008, 36(1): 99-104. |
| [6] | 周鹏, 秦树人. 基于切片谱免疫系统的旋转机械故障诊断[J]. 仪器仪表学报, 2008, 29(6): 1198-1202. Zhou P, Qin S R. Rotating machinery fault diagnosis based on slice spectrum-AIS[J]. Chinese Journal of Scientific Instrument, 2008, 129(6): 1198-1202. |
| [7] | 朱冰莲, 田学隆, 宋维佳. 基于人工免疫系统的医学图像配准[J]. 仪器仪表学报, 2009, 30(7): 1416-1419. Zhu B L, Tian X L, Song W J. Medical image registration algorithm based on artificial immune system[J]. Chinese Journal of Scientific Instrument, 2009, 30(7): 1416-1419. |
| [8] | 赵鹏, 王友仁, 崔江, 等. 模拟电路免疫记忆网络故障诊断方法[J]. 信息与控制, 2010, 39(5): 574-580. Zhao P, Wang Y R, Cui J, et al. Fault diagnosis method for analog electronic circuits based on immune memory network theory[J]. Information and Control, 2010, 39(5): 574-580. |
| [9] | Dasgupta D, Yu S, Nino F. Recent advances in artificial immune systems: Models and applications[J]. Applied Soft Computing, 2011, 11(2): 1574-1587. |
| [10] | dos Anjos Lima F P, Chavarette F R, dos Santos e Souza A, et al. Artificial immune systems with negative selection applied to health monitoring of aeronautical structures[J]. Advanced Materials Research, 2013, 871(1): 283-289. |
| [11] | 李睿. 基于时域响应特征提取与异常检测的结构损伤诊断方法研究[D]. 长沙: 湖南大学, 2007. LI R. The research on structural damage detection methods based on feature extraction and outlier detction with time domian response[D]. Changsha: Hunan University, 2007. |
| [12] | Chen B, Zang C Z. Artifical immune pattern recognition for damage detection in structure health monitoring sensor networks[C]//Proceedings of the SPIE. Bellingham, WA, USA: SPIE, 2009: 72930k. |
| [13] | Mojtahedi A, Lotfollahi Y M A, Hassanzadeh Y, et al. A robust damage detection method developed for offshore jacket platforms using modified artificial immune system algorithm[J]. China Ocean Engineering, 2012, 26(3): 379-395. |
| [14] | 江斌. 人工免疫算法的基础研究及其应用[D]. 长沙: 中南大学, 2008. Jiang B. Basic research and applications of artificial immune algorithm[D]. Changsha: Central South University, 2008. |
| [15] | Moncayo H, Perhinschi M G, Davis J. Aircraft failure detection and identification over an extended flight envelope using an artificial immune system[J]. Aeronautical Journal, 2011, 115(1163): 43-55. |
| [16] | 陈颖, 徐晓晖, 李志全. 基于免疫克隆原理的改进粒子群优化算法的研究[J]. 系统仿真学报, 2008, 20(6): 1471-1474.Chen Y, Xu X H, Li Z Q. Study of modified particle swarm optimization algorithm based on immune clone principle[J]. Journal of System Simulation, 2008, 20(6): 1471-1474. |
| [17] | de Castro L N, von Zuben F J. Learning and optimization using the clonal selection principle[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(3): 239-251. |
| [18] | Theodoridis S, Koutroumbas K. Pattern recognition[M]. New York, USA: Academic Press, 2008. |
| [19] | Johnson E A, Lam H F, Katafygiotis S, et al. A benchmark problem for structural health monitoring and damage detection[M]//Structural Control for Civil and Infrastructure Engineering. Singapore: World Scientific Publish Co., 2001: 317-324. |
| [20] | Chen B, Zang C Z. Artificial immune pattern recognition for structure damage classification[J]. Computers and Structures, 2009, 87(21/22): 1394-1407. |



