2. 东北大学流程工业综合自动化国家重点实验室, 辽宁 沈阳 110819;
3. 中铝瑞闽股份有限公司装备能源部, 福建 福州 350015
2. State Key Laboratory of Synthetic Automation for Process Industries, Northeastern University, Shenyang 110819, China;
3. Equipment Department of Energy, Chalco Ruimin Co., Ltd, Fuzhou 350015, China
1 引言
为了使轧制出的板带材具有较高厚度精度,一级控制系统中的压力自动厚度控制(automatic gauge control,AGC)和监控AGC经常一起投入使用[1, 2]. 压力AGC主要用于消除轧件扰动因素引起的板带厚度偏差[3, 4, 5],对于设定不准确而导致的趋势性板带厚差,则需要监控AGC对其进行监控和校正[6, 7, 8].
监控AGC利用精轧机组出口处的测厚仪检测终轧板带厚差,将该厚差按照设置的厚差分配系数分配给具有监控AGC功能的机架,相应机架通过调节辊缝来修正分配到的厚差,从而消除终轧板带厚差[9],达到对终轧板带厚度进行监控和修正的目的. 针对同一块板带材,传统监控AGC的厚差分配策略是不变的,所以,传统监控AGC无法在快速修正终轧板带厚差的同时考虑板形质量. 中铝瑞闽引进的“1+3”热精轧机组中,采用德国西门子为其设计的一种新型监控AGC[10]. 该监控AGC的厚差分配策略在厚差修正过程中是动态变化的,使得该监控AGC具备快速消除终轧板带厚差和合理厚差再分配以利于板形控制的能力.
由于受轧制板带材规格的限制,新型监控AGC的厚差分配系数依据轧制经验设置为常数,这使得新型监控AGC在厚差修正时只能对部分牌号的铝合金进行近似合理厚差再分配以利于板形控制. 而在轧制其它牌号铝合金或者开发新品种时,则无法进行合理的厚差再分配,进而导致板形质量恶化. 这不仅没有充分发挥新型监控AGC的特性,而且会给弯辊控制系统带来额外负担. 针对上述问题,文[11]和文[12]对传统监控AGC进行了研究. 文[11]通过计算Fi机架辊缝调节量与终轧板带厚差之间的影响系数来确定相应机架辊缝调节量. 在计算过程中,该方法需要调用轧制力计算公式,但该计算公式计算量大且计算程度复杂. 文[12]通过计算Fi机架相对轧制力来确定相应机架辊缝调节量. 但是,计算过程中并未考虑机架间厚度变化对轧制力的影响.
本文首先对新型监控AGC的控制策略进行研究,并分析厚差分配系数设置为常数时存在的问题;然后,通过理论推导出合理厚差分配需要满足的规则;针对厚差分配系数存在的问题,同时为克服文[11]和文[12]中研究方法的缺点,基于新型监控AGC的控制策略、 合理厚差分配的规则及轧制理论,推导出控制器可以直接使用的厚差分配系数的计算公式,使计算出的厚差分配系数在轧制材料发生变化时,能够保证新型监控AGC进行合理厚差再分配以利于板形控制. 最后,将改进计算的厚差分配系数应用于监控AGC系统中,对轧制不同规格的铝板带进行仿真验证.
2 新型监控AGC及存在的问题图 1为瑞闽热精轧机组采用的新型监控AGC示意图.
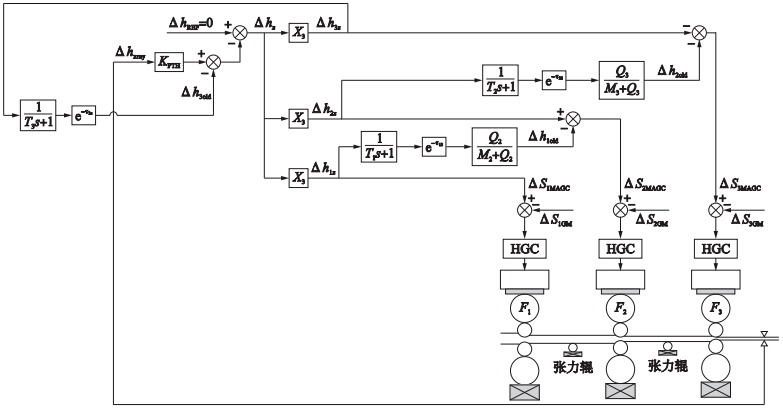 |
| 图 1 新型监控AGCFig. 1 The new monitor AGC |
图中Xi(i=1,2,3)为Fi机架的厚差分配系数,HGC(hydraulic gap control)为液压辊缝控制系统,ΔSiMAGC(i=1,2,3)为Fi机架的辊缝调节量设定值,Mi和Qi(i=2,3)分别为Fi机架的轧机刚度和轧件塑性系数,ΔhREF为新型监控AGC允许的厚度偏差,一般ΔhREF=0,Δhxray为多功能凸度仪检测到的终轧板带厚差,KPTH为比例系数,Δhiold(i=1,2,3)为分配给Fi机架及其上游机架修正的板带厚差,初始时刻Δhiold=0,Δhx为新型监控AGC需要修正的终轧板带厚差,Δhix(i=1,2,3)为分配给Fi机架修正的板带厚差,T1、 T2和T3为Fi机架的轧机模型近似成一阶模型时的惯性时间常数,τ12、 τ23和τ3x分别为板带材从F1机架到F2机架、 F2机架到F3机架和F3机架到凸度仪的运行时间.
新型监控AGC将终轧板带厚差、 目标板带厚差和分配给F3机架及其上游机架修正的板带厚差进行比较,求得需要修正的终轧板带厚差
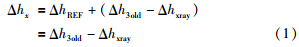
在式(1)计算出需要修正的终轧板带厚差后,利用确定的厚差分配系数Xi计算出分配给各机架修正的板带厚差,然后直接将其作为辊缝调节量设定值
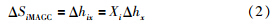
当跟踪到F3机架处板带材上的监控AGC修正点到达凸度仪时,测量新的终轧板带厚差. 新型监控AGC在上一次修正值Δh3old的基础上,按照式(1)和式(2)的计算值给出第二次辊缝调节量设定值去修正新的终轧板带厚差.
由图 1可知,F1、 F2和F3机架与凸度仪的距离依次递减. 因此,为了能够尽快消除终轧板带厚差,缩短板带厚度的超差长度,新型监控AGC的厚差分配策略规定厚差分配系数Xi满足如下关系

由图 1中F1~F3机架与凸度仪的相对位置和式(3)中各机架厚差分配系数的关系可知,式(2)计算的分配给各机架修正的板带厚差随着机架到凸度仪的距离的缩短而增加,这将使末机架轧出的板带厚度很快达到目标板带厚度.
由于各机架修正的板带厚差随着机架到凸度仪的距离的缩短而增加,导致各机架修正板带厚差引起的轧制力变化量也随着机架到凸度仪的距离的缩短而增加. 为了避免过大的轧制力变化量对板形质量产生影响[13],新型监控AGC在厚差修正过程中改变厚差分配策略进行厚差再分配降低下游机架的厚差修正量,进而降低相应机架的轧制力变化量以利于板形控制. 具体做法是:当跟踪到Fi-1(i=2,3)机架处板带材上的监控AGC修正点到达Fi机架时,将Fi机架的厚差分配系数从Xi变为Xi-Xi-1QiMi+Qi. 由式(4)可以重新计算出分配给Fi机架的板带厚差,并作为辊缝调节量设定值

由连轧过程的工艺条件可知,Fi-1机架修正的板带厚差就是Fi机架入口板带厚度的变化量. 因此,依据轧制理论中机架入口厚度偏差与出口厚度偏差的关系式(式(5))[14],可将Fi-1机架的厚差修正量Δhix转换为Fi机架的厚差修正量,如式(6)所示.
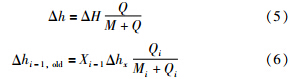
结合式(4)和式(6)可知,新型监控AGC进行厚差再分配,相当于从分配给Fi机架的厚差修正量中减掉分配给Fi-1机架的厚差修正量,即实现Fi-1和Fi机架之间的厚差再分配,降低Fi机架的厚差修正量及其引起的轧制力变化量. 当F1机架处板带材上的监控AGC修正点通过F3机架时,就可以实现F1~F3机架的厚差再分配. 如果厚差分配系数X1和X2设置合理,可实现F1~F3机架的合理厚差再分配.
新型监控AGC的控制过程就是在厚差修正过程中循环改变厚差分配策略,进行厚差修正和厚差再分配的调节过程,直至厚差修正完毕.
综上可知,新型监控AGC具备快速消除终轧板带厚差和合理厚差再分配的能力.
由式(2)和式(4)可知,厚差分配系数直接影响分配给各机架的厚差修正量. 由于厚差修正量引起的轧制力变化量会进一步影响板形质量,如果厚差分配系数设置不合理,会使新型监控AGC分配的厚差修正量不合理,进而导致板形质量恶化,增加弯辊控制系统的调节负担. 由于受轧制板带材规格的限制,F1和F2机架的厚差分配系数依据轧制经验设置为常数,对轧制不同牌号的铝板带使用相同的厚差分配系数进行厚差分配. 虽然最终都可以消除终轧板带厚差,但只能使新型监控AGC在轧制部分牌号的铝板带时,可以近似地进行合理厚差再分配,从而减少厚差分配不合理对板形质量的影响. 而在轧制材料发生变化或者开发新品种时,甚至无法近似进行合理厚差再分配,这使得新型监控AGC合理厚差再分配的能力没有得到充分发挥.
3 合理厚差分配规则为了使新型监控AGC在厚差修正后能够进行合理厚差再分配,以利于板形控制,需要知道如何分配厚差才能使监控AGC在厚差修正前后保持板形良好,即需要知道合理厚差分配所遵循的规则.
假设负荷分配计算已经使轧制的板带材满足板形良好条件[15, 16, 17],且终轧板带厚差修正后,仍然能够保持板形良好. 由板形良好条件可知,各机架出口处板带相对凸度相等[18].

由式(8)可得:
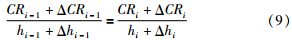
凸度采用有载辊缝方程来描述[18]:
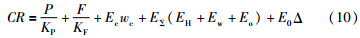
假设来料平直度良好,忽略弯辊力、 可控辊型和轧辊状态缓慢变化对板带凸度的影响,则式(10)可简化为

由式(11)可得其增量形式为

依据轧制理论可知,监控AGC调节辊缝修正的板带厚差和其引起的轧制力变化量的关系为

联合式(12)和式(13)可得
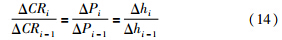
结合式(7)、 式(9)和式(14)可得
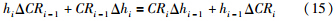
在板形良好的条件下,各机架出口处的板带相对凸度增量保持不变[19]

将式(15)两边同时除以hihi-1,然后结合式(7)和式(16)可得

将式(17)两侧同时加1,可得
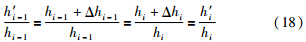
最后,结合式(7)、 式(8)、 式(11)和式(18)可得
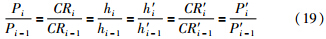
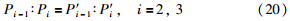
由以上推导可知,为使监控AGC在终轧板带厚差修正前后保持板形良好,需各机架的轧制力分配比例在厚差修正前后保持不变,如式(20)所示.
4 厚差分配系数的改进计算在终轧板带厚差修正前后保持各机架轧制力的分配比例不变,相当于各机架的相对轧制力变化量满足以下关系:
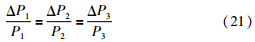
当板带材头部运行到末机架与凸度仪之间时,由于各机架的厚度计AGC已经开始运行,因此,厚度计AGC设定或锁定的轧制力Pi已知. 由式(21)可进一步确定各机架轧制力变化量之间的比值为

依据新型监控AGC厚差修正时的厚差分配策略,将F3机架的厚差分配系数设置为X3=1. 因此,只要找到F1和F2机架的厚差分配系数与相应机架轧制力变化量之间的关系,并依据式(22)和式(23)确定的方程组,即可解得另外2个机架的厚差分配系数.
假设板带材穿带结束,各机架厚度计AGC已经确定设定或锁定轧制力,并进入稳定运行. 终轧板带厚度存在一个稳定的厚度偏差,当板带材到达凸度仪时,检测到该厚度偏差为Δhxray,依据式(1)即可计算出需要修正的厚度偏差Δhx. 监控AGC修正结束后,3个机架的辊缝修正量如式(2)所示.
依据辊缝变化量与厚度变化量之间的关系[18],由式(2)可以计算出各机架修正的厚度偏差为

对于连轧机而言,上游机架出口板带厚度的变化量即下游机架入口板带厚度的变化量,因此,有式(25)成立

已知轧机入口板带厚差、 辊缝调节量和轧机出口板带厚差的关系为[20]
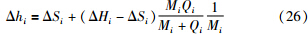
将式(26)与轧机弹跳方程的增量式式(27)对比可得轧制力变化量,如式(28)所示.
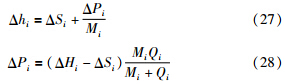
由式(22)~式(28)可得

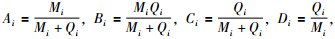
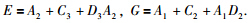
对式(29)求解,得到控制器可以直接使用的式子:
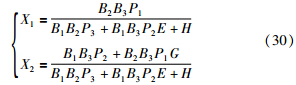
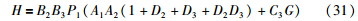
在厚度计AGC确定设定或锁定轧制力后、 监控AGC工作前,将Fi机架厚度计AGC设定或锁定的轧制力带入式(30),即可解出针对本块料的F1和F2机架的厚差分配系数.
5 仿真实验以瑞闽热精轧机组3个机架为例,分别轧制两种规格的铝合金. 其中规格1的铝合金牌号为5052,提取其现场生产数据如表 1所示.
| 机架号 | F1 | F2 | F3 |
| 轧机刚度/(kN/mm) | 5 600 | 5 200 | 5 000 |
| 轧件塑性系数/(kN/mm) | 1 200 | 1 700 | 1 900 |
| 厚度计AGC设定轧制力/kN | 21 478.3 | 12 165.7 | 5 787.7 |
| 轧制速度/(m/s) | 1.22 | 2.6 | 5 |
机架间距离为5.5 m,末机架到测厚仪的距离为2.45 m. 利用表 1中的轧制速度和上述距离可以计算得到板带材在机架间的运行时间和末机架到凸度仪的运行时间[τ12,τ23,τ3x]=[4.5,2.12,0.49] s. 程序中的原厚差分配系数和采用本文方法计算的改进厚差分配系数如表 2所示. 各机架辊缝调节量和成品板带厚差曲线如图 2所示.
| 系数 | 原系数 | 改进系数 |
| X1 | 0.45 | 0.439 9 |
| X2 | 0.75 | 0.781 3 |
| X3 | 1 | 1 |
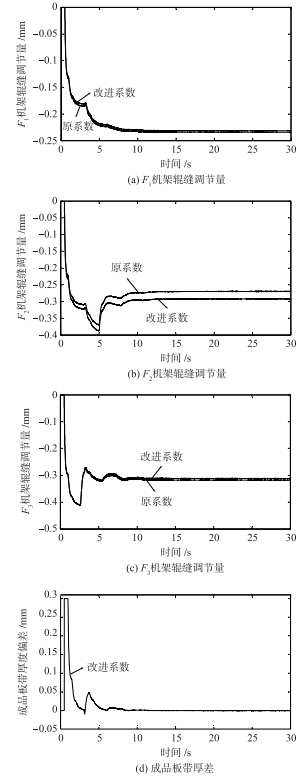 |
| 图 2 规格1铝合金的各机架辊缝调节量和成品板带厚差Fig. 2 Gap adjustment in each stand and strip thickness deviation for the finished product of the first specification aluminum alloy |
由图 2(a)~2(c)可知,F1机架辊缝调节量直接达到目标位置,F2和F3机架的辊缝调节量分别在4.99 s和2.61 s回调后达到目标位置. F2和F3机架辊缝调节量的回调是由于厚差修正过程中新型监控AGC厚差分配策略的动态变化造成的. 由新型监控AGC的厚差分配策略可知,在厚差修正时,各机架的厚差修正量随着机架距离凸度仪距离的缩短而增加,导致修正厚差引起的轧制力变化量也随着机架距离凸度仪距离的缩短而增加. 为了避免过大的轧制力变化量对板形质量产生影响,当Fi-1(i=2,3)机架处板带材上的监控AGC修正点到达Fi机架时,新型监控AGC改变厚差分配策略,通过厚差再分配来降低分配给F2和F3机架的厚差修正量,所以,F2和F3机架的辊缝调节量会回调. 由于原厚差分配系数和改进厚差分配系数不同,所以采用两种厚差分配系数的辊缝调节量在各机架中是不同的. 但是,最终都能够消除终轧板带厚差. 由于采用两种厚差分配系数的终轧板带厚差曲线没有差别,所以只给出采用改进厚差分配系数的终轧板带厚差曲线,如图 2(d)所示.
新型监控AGC完成终轧板带厚差修正和厚差再分配后,其厚差分配策略不再发生变化. 在厚差再分配后,采用原厚差分配系数的各机架实际轧制力为[P1old,P2old,P3old]=[21 710,12 265,5 880.5] kN,其比值为[P1old/P3old,P2old/P3old]=[3.691 9,2.085 7];采用改进厚差分配系数的各机架实际轧制力为[P1new,P2new,P3new]=[21 707,12 296,5 849.8] kN,其比值为[P1new/P3new,P2new/P3new]=[3.711,2.102];由表 1中各机架厚度计AGC设定轧制力可知其比值为[P1/P3,P2/P3]=[3.711,2.102]. 综上可知,采用原厚差分配系数的新型监控AGC只能近似保持轧制力分配比例不变;而采用改进厚差分配系数的新型监控AGC不仅能确保轧制力分配比例不变,还能更好地进行合理厚差再分配.
为了方便比较采用两种厚差分配系数的新型监控AGC修正板带厚度偏差对板形质量的影响,图 3分别给出F1与F2机架和F2与F3机架的相对凸度增量差曲线.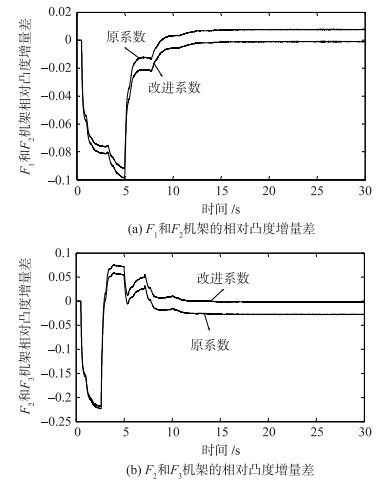 |
| 图 3 规格1铝合金的相对凸度增量差Fig. 3 Increment difference of relative crown of the first specification aluminum alloy |
由图 3可知,采用改进厚差分配系数的新型监控AGC,在厚差修正前后能够严格保持相对凸度增量差不变,且比采用原厚差分配系数的新型监控AGC更能进行合理厚差再分配,以利于板形控制.
规格2铝合金牌号为5182,提取其现场生产数据如表 3所示.
| 机架号 | F1 | F2 | F3 |
| 轧机刚度/(kN/mm) | 5 800 | 5 500 | 5 300 |
| 轧件塑性系数/(kN/mm) | 2 800 | 3 000 | 4 500 |
| 厚度计AGC设定轧制力/kN | 26 817 | 16 159.8 | 13 500 |
| 轧制速度/(m/s) | 1.61 | 2.76 | 4.6 |
依据上述距离参数及表 3中的轧制速度计算得到板带材在机架间的运行时间和末机架到凸度仪的运行时间[τ12,τ23,τ3x]=[3.42,1.99,0.53] s. 采用本文方法计算的改进厚差分配系数为[X1,X2,X3]=[0.307 8,0.609 9,1]. 采用原厚差分配系数和改进的厚差分配系数对规格2铝合金进行仿真.
新型监控AGC调节结束后,采用原厚差分配系数的各机架实际轧制力为[P1old,P2old,P3old]=[28 015,16 494,13 322] kN,则其比值为[P1old/P3old,P2old/P3old]=[2.102 9,1.238 1];采用改进厚差分配系数的各机架实际轧制力为[P1new,P2new,P3new]=[27 563,16 609,13 875] kN,其比值为[P1new/P3new,P2new/P3new]=[1.986 5,1.197];由表 3中的各机架厚度计AGC设定轧制力可知其比值为[P1/P3,P2/P3]=[1.986 4,1.196 9]. 因此,采用改进厚差分配系数的新型监控AGC在轧制规格2铝合金时,能够准确地保持各机架轧制力分配比例不变. 新型监控AGC修正终轧板带厚差对板形质量的影响如图 4中相对凸度增量差曲线所示.
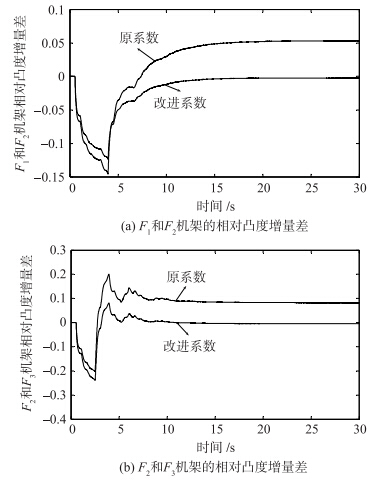 |
| 图 4 规格2铝合金的相对凸度增量差Fig. 4 Increment difference of relative crown of the second specification aluminum alloy |
由图 4中可知,采用原厚差分配系数的新型监控AGC在厚差修正后无法进行合理厚差再分配,使得相对凸度增量差无法回到初始值,从而导致板形质量恶化,给弯辊控制系统增加较大的调节负担. 采用改进厚差分配系数的新型监控AGC,在厚差修正前后能够准确地保持相对凸度增量差不变以利于板形控制.
5 结论本文通过对新型监控AGC控制策略的介绍和分析,总结新型监控AGC的特点:具有快速修正终轧板带厚度偏差和合理厚差再分配的能力;给出监控AGC厚差修正后合理分配厚差需要满足的规则:保持各机架轧制力分配比例不变;依据保持各机架轧制力分配比例不变的规则和新型监控AGC的控制策略,推导出F1和F2机架的厚差分配系数的计算公式. 该公式可以由控制器直接使用,使厚差分配系数能够适应轧制铝合金牌号变化以利于板形控制,充分发挥新型监控AGC的合理厚差再分配的能力;在轧制不同牌号的铝合金时,改进厚差分配系数使新型监控AGC充分发挥合理厚差再分配的能力,在厚差修正前后,能够准确地保持轧制力分配比例不变以利于板形控制.
| [1] | Tan S B, Zhong Y F, Xu X H. Decoupling control of automatic gauge control system in hot-rolling mills[C]//Proceedings of the IEEE International Conference on Industrial Technology. Piscataway, NJ, USA: IEEE, 2005: 552-555. |
| [2] | 李仲德, 杨卫东. 冷连轧AGC系统的自适应Smith广义预测控制[J]. 信息与控制, 2009, 38(5): 575-579. Li Z D, Yang W D. Adaptive Smith generalized predictive control for AGC system of tandem cold rolling[J]. Information and Control, 2009, 38(5): 575-579. |
| [3] | Ji Y F, Zhang D H, Chen S Z, et al. Algorithm design and application of novel GM-AGC based on mill stretch characteristic curve[J]. Journal of Central South University of Technology, 2014, 21(3): 942-947. |
| [4] | 王君, 张殿华, 王国栋. 厚度计型和动态设定型AGC的统一性证明[J]. 控制与决策, 2000, 15(3): 333-335. Wang J, Zhang D H, Wang G D. Verification of the uniformity of gauge meter and dynamic set AGC[J]. Control and Decision, 2000, 15(3): 333-335. |
| [5] | 孙杰, 张殿华, 李旭, 等. 厚度计AGC应用中存在的问题及对策[J]. 东北大学学报: 自然科学版, 2009, 30(11): 1621-1623. Sun J, Zhang D H, Li X, et al. Existing problems of gauge meter AGC in application and solutions[J]. Journal of Northeastern University: Natural Science, 2009, 30(11): 1621-1623. |
| [6] | Sun J, Zhang D H, Li X, et al. Smith prediction monitor AGC system based on fuzzy self-tuning PID control[J]. Journal of Iron and Steel Research International, 2010, 17(2): 22-26. |
| [7] | 王丽君, 童朝南, 李擎, 等. 实用自抗扰控制在大时滞厚度自动监控系统中的应用[J]. 控制理论与应用, 2012, 29(3): 368-374. Wang L J, Tong C N, Li Q, et al. Practical active disturbance rejection solution for monitoring automatic gauge control system with large time-delay[J]. Control Theory and Applications, 2012, 29(3): 368-374. |
| [8] | Zhang H Y, Sun J, Zhang D H, et al. Improved Smith prediction monitoring AGC system based on feedback-assisted iterative learning control[J]. Journal of Central South University of Technology, 2014, 21(9): 3492-3497. |
| [9] | Zhang D H, Zhang H, Sun T, et al. Monitor automatic gauge control strategy with a Smith predictor for steel strip rolling[J]. Journal of University of Science and Technology Beijing, 2008, 15(6): 827-832. |
| [10] | Li D, Liu J C, Tan S B, et al. A new monitor-AGC system in hot continuous rolling[C]//Proceedings of the Control Conference. Piscataway, NJ, USA: IEEE, 2014: 6319-6323. |
| [11] | Li B Q, Bian L, Sun Y K. On application of one-step arithmetic in FMN to hot continuous rolling[C]//Proceedings of the Control and Decision Conference. Piscataway, NJ, USA: IEEE, 2009: 5841-5846. |
| [12] | 黄涛, 张杰, 曹建国, 等. 基于保持负荷分配比例的快速监控AGC[J]. 钢铁研究学报, 2008, 20(6): 23-26. Huang T, Zhang J, Cao J G, et al. Fast monitor AGC based on balance of rolling force distribution[J]. Journal of Iron and Steel Research, 2008, 20(6): 23-26. |
| [13] | 王国栋. 板形控制和板形理论[M]. 北京: 冶金工业出版社, 1986: 512-513. Wang G D. Flatness control and theory[M]. Beijing: Metallurgical Industry Press, 1986: 512-513. |
| [14] | 姬亚锋, 张殿华, 孙杰, 等. 热连轧机AGC系统的优化[J]. 东北大学学报: 自然科学版, 2013, 34(4): 532-535. Ji Y F, Zhang D H, Sun J, et al. Optimization of AGC system for hot strip mills[J]. Journal of Northeastern University: Natural Science, 2013, 34(4): 532-535. |
| [15] | Li W G, Liu X H, Guo Z H. Multi-objective optimization for draft scheduling of hot strip mill[J]. Journal of Central South University of Technology, 2012, 19(11): 3069-3078. |
| [16] | 姚峰, 杨卫东, 张明. 多目标差分进化在热连轧负荷分配中的应用[J]. 控制理论与应用, 2010, 27(7): 897-902. Yao F, Yang W D, Zhang M. Multi-objective differential evolution used for load distribution of hot strip mills[J]. Control Theory and Applications, 2010, 27(7): 897-902. |
| [17] | Jia S J, Li W G, Liu X H, et al. Multi-objective load distribution optimization for hot strip mills[J]. Journal of Iron and Steel Research International, 2013, 20(2): 27-32, 61. |
| [18] | 孙一康. 带钢热连轧的模型与控制[M]. 北京: 冶金工业出版社, 2002: 144-171. Sun Y K. The model and control of hot strip mill[M]. Beijing: Metallurgical Industry Press, 2002: 144-171. |
| [19] | 戚向东, 董志奎, 连家创, 等. 热连轧板凸度闭环控制的工业应用[J]. 钢铁, 2013, 48(5): 51-54. Qi X D, Dong Z K, Lian J C, et al. Application of strip crown closed-loop control for hot strip mill[J]. Iron and Steel, 2013, 48(5): 51-54. |
| [20] | 谭树彬, 钟云峰, 徐心和. 板带轧机变刚度控制的应用及仿真[J]. 系统仿真学报, 2006, 18(4): 1030-1032. Tan S B, Zhong Y F, Xu X H. Simulation and application of mill modulus control in strip rolling mills[J]. Journal of System Simulation, 2006, 18(4): 1030-1032. |



