文章快速检索  
  高级检索
引用本文
沈俊鹏, 黄静雯, 李宏光, 刘操. 面向过程经济性能优化的最优性条件在线预测与实现[J]. 信息与控制, 2015, 44(4): 449-454
SHEN Junpeng, HUANG Jingwen, LI Hongguang, LIU Cao. An On-line Prediction and Implementation of Necessary Conditions of Optimality towards Process Economic Optimization[J]. INFORMATION AND CONTROL, 2015, 44(4): 449-454.
面向过程经济性能优化的最优性条件在线预测与实现
沈俊鹏, 黄静雯, 李宏光, 刘操    
北京化工大学, 北京 100029
收稿日期: 2014-08-15; 录用日期: 2014-11-10; 修回日期: 2014-12-29
基金项目: 中央高校基本科研业务费专项基金资助项目（YS1404）；国家质检总局科技计划资助项目（2015IK048）.
作者简介: 沈俊鹏（1988-），男，硕士．研究领域为大系统分解，过程优化与控制．
黄静雯（1981-），女，博士，讲师．研究领域为全厂过程实时优化，控制理论与应用，智能控制．
通讯作者: 李宏光（1963-），男，教授，博士生导师．研究领域为智能协调与优化控制，过程报警优化与管理，情感交互多目标优化与决策，lihg@mail.buct.edu.cn
摘要: 选择包含系统的约束条件和梯度信息的最优性条件（necessary conditions of optimality，NCO）作为控制系统的实现目标，可以从结构设计角度有效地提高生产过程的经济性能．针对NCO在线不易直接测量、离线估计不及时和不准确等问题，提出了一类基于高斯过程的NCO建模、预测及控制方法．通过生产过程实时数据在线动态更新高斯过程模型，实时准确预测NCO的值，以决策下一时刻的最优控制率，实现生产过程对经济性能最优值的跟踪．对一个化工过程实例进行了仿真，结果验证了该方法的有效性．
关键词: 高斯过程     经济性能     在线预测     优化控制    
An On-line Prediction and Implementation of Necessary Conditions of Optimality towards Process Economic Optimization
SHEN Junpeng, HUANG Jingwen, LI Hongguang , LIU Cao     
Beijing University of Chemical Technology, Beijing 100029, China
Abstract: The economic performance of plants can be effectively improved in terms of control system structure optimization through the selection of necessary conditions of optimality (NCOs), including constraint and gradient information, as the implementation targets of control systems. In response to the difficulties in direct online measurements and in timely and accurate offline estimations of NCOs, a novel approach to NCO modeling, prediction, and control based on a Gaussian process is proposed. To process real-time data, the proposed process can update the Gaussian process model dynamically online and the NCOs can be accurately predicted to enable the best decision of the optimal control rate for the next moment, thereby enabling process economic performance to achieve optimality. The proposed approaches are applied to an exemplary chemical process simulation, and the results show the effectiveness of the proposed method.
Key words:
Gaussian process     economic performance     on-line prediction     optimal control    

1 引言

对于复杂的工业生产过程，控制系统的结构设计会直接影响到生产过程的经济性能，因此，被控变量的选取在“结构性”[1, 2, 3]决策中具有重要作用，而自主优化控制(self-optimizing control，SOC)[4, 5]为合理选取被控变量提供了思路.

最优性条件(necessary conditions of optimality，NCO)是非线性规划问题获得最优解所需满足的充分必要条件[6, 7]. Francois和Bonvin等[8, 9]使用NCO跟踪技术来寻找最优控制率； Mohammad和Jaschke等[10, 11]提出将NCO与自主优化控制相结合，把NCO作为控制系统的实现目标，即被控变量或被控目标，并采取双层控制策略. 基于这种思想，Ye等[12]采取神经网络全局离线拟合与局部在线估计等方式估计NCO. 研究表明，基于NCO的控制策略有效地提高了优化控制效果. 然而，NCO与自主优化控制相结合的优化控制策略依赖于控制对象模型的准确性和对NCO估计量的精度[13, 14]，而无论是对NCO的全局离线拟合还是局部在线估计都很难达到期望的精度要求[15].

许多生产过程的噪声与测量变量都具有高斯过程特性. Rasmussen等[16]率先将高斯过程应用于机器学习领域. 由于高斯过程模型具有建模灵活、 参数少、 易收敛等特点，基于此方法的控制技术也得到了较快的发展[17, 18]. Kocijan和Murray-Smith等[19]首次将高斯过程应用于系统辨识与模型预测控制中，通过仿真实例可以看出由于高斯过程加入了先验知识，使得系统的鲁棒性得以提高. 近年来，新的研究表明，高斯过程在复杂工业过程建模方面具有良好的拟合效果与泛化能力[20].

本文根据面向生产过程经济性能优化控制的要求，提出基于高斯过程的NCO在线预测和实现方法，结合过程数据在线动态更新高斯过程模型，准确预测NCO的实时值，决策下一时刻的最优控制率，实时跟踪最优值，提高了过程经济指标与优化控制性能.

2 NCO在线预测算法

对于连续过程的优化控制问题，在约束条件下，运用一些优化控制策略使目标函数最大(或最小). 在通常情况下，优化控制问题可以表述为如下数学模型：

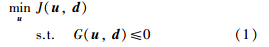
其中： J是优化目标函数，通常是指经济目标或者代价函数，u是操纵变量，d是扰动，G是约束条件.

NCO是在满足一些规则条件下，一个优化问题能够有最优解的条件. 在约束边界上的条件记为Ga，并且有Ga(u*，d)=0，即NCO为

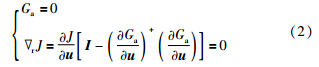
其中： Ga是积极约束条件，通常是指生产过程的安全要求、 生产规格、 设备容限等，在多数情况下，这些都是在线可测量的. ∇rJ是系统梯度信息，含有形式复杂的微分成分，并且依赖于不可测扰动，因此难以在线获得. 后文如无特别说明，涉及到的NCO均指代∇rJ，即NCO的梯度部分.

在优化过程中，在不确定因素影响下，如果操作是最优的(u=u*)，则必有式(2)成立，生产过程也一定处于最优工况.

高斯过程服从正态分布，高斯过程模型的选择可以看成是定义了一个非线性函数的先验概率分布，而训练过程则可以看作是得到该函数的后验概率分布. 因此在NCO的高斯过程在线建模中，本文以系统的输入输出数据作为训练样本集，以核函数作为先验知识，通过训练过程，获得高斯过程初始模型，根据系统参数变化或噪声干扰，在线动态更新样本集、 超参数向量与高斯过程模型，准确预测NCO的值. 本文使用如下的建模方法.

高斯过程训练样本集D可表述为

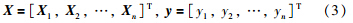
其中： Xi=[X1，X2，…，Xm]T(1≤i≤n)为系统的m个测量变量，y=[y1，y2，…，yn]T为NCO的值.

高斯过程需要确定协方差函数(核函数)，这里选取最常用的径向基函数作为核函数，即：

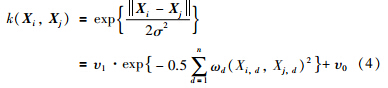
其中： Xi，d、 Xj，d表示Xi、 Xj的第d个分量，ωd表示各分量的加权值，υ0表示扰动大小，υ1表示不相关性放大倍数.

核函数的输入值在输入空间的位置越接近时，与其所对应的函数输出值之间的相关性越大； 反之，则相关性越小.

核函数的超参数向量为

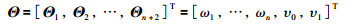
其中参数ω1，…，ωn表示特征长度尺度，它们决定着输入空间中的每一维数据在核函数中所占的权重大小.

对于输出是连续实数值的回归问题，本文从“函数空间论”和“权重值空间论”方面进行高斯建模，通过训练得到高斯过程初始模型，其预测输出均值为

预测值的方差为

其中： k(·，·)为模型选择的协方差函数，x*是测试变量，K(X，X)代表n×n的训练样本的协方差矩阵，其表示为Kij=k(Xi，Xj)(1≤i，j≤n). K(x*，X)=[k(x*，X1)…k(x*，Xn)]为多个协方差的一行n列矩阵.

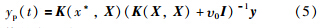
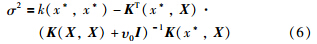
面对时变或干扰较大的系统，需在线更新高斯过程模型. 该问题的关键在于超参数向量与样本集的实时更新. 考虑在线建模的实时性，本文采用基于“自然梯度”的在线高斯建模算法，其超参数向量的更新率为

其中：

其中，ηk表示学习率，εk表示时间学习率，∇l(Θk)为对数似然函数的梯度对各个超参数的偏导数，Gk是Fisher信息矩阵，Gk-1是对Gk的估计.

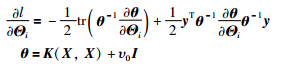
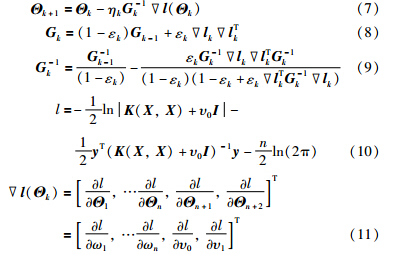
NCO在线预测迭代算法如下：

步骤1： 初始化超参数向量Θk、 置k=1，选择合适的核函数k(Xi，Xj)、 学习率ηk以及时间学习率εk.

步骤2：采集得到n组数据集｛Xi，yi｝i=1n作为高斯过程的样本集，通过训练获得高斯过程初始模型. 样本集中的数据要尽可能的具有代表性，在空间中的分布不能太接近，为了保证泛化能力，尽量使输入空间中的数据均匀分布.

步骤3： 根据超参数向量Θk与生产过程测量变量Xi，计算NCO的预测值yp(k).

步骤4： 当k时刻的预测值施加给系统后，便可以采集到输出值. 此时将新的样本值放入到高斯过程的样本集Xi=[x1，x2，…，xm]T，y=[y1，y2，yn]T中，样本集增加一个新样本的同时也剔除一个旧样本，保证样本集n不变.

步骤5： 根据新的样本集以及式(7)～式(11)来更新下一时刻超参数向量Θk+1. 由于训练样本集与超参数向量的改变，高斯过程模型得到更新.

步骤6： 令k=k+1，转入下一时刻，重复步骤3，直到优化控制过程结束. NCO在线预测迭代算法流程如图 1所示.

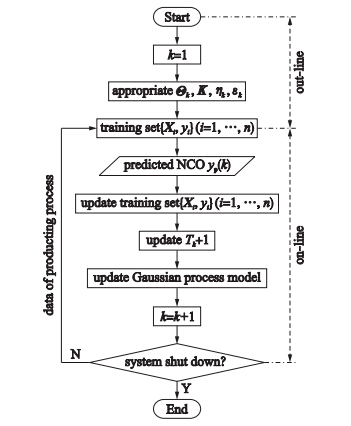图 1 NCO在线预测迭代算法流程图Fig. 1 The algorithmic flow chart of on-line iterative predictions of NCO
图选项
3 NCO实现策略

基于自主优化控制思想，选取NCO作为面向经济性能优化的控制系统实现目标，后文简称被控变量，运用简单的定值控制，可以在常见扰动下使目标函数的最优性得以保证. 注意到在式(2)中，在最优工况时，NCO的值为0. 因此如果选取NCO作为被控变量，并使NCO的设定点为0，在控制器的作用下使其成立或近似成立，则在此时生产过程即处于最优经济性能指标. 这样就把优化控制问题转化为定值跟踪问题，构造的控制系统如图 2所示.

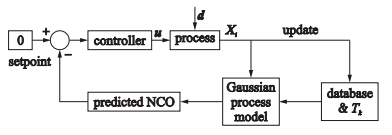图 2 基于高斯过程模型的NCO控制系统Fig. 2 NCO control system based on Gaussian process model
图选项

由于系统存在扰动d，生产过程测量变量Xi不断变化，使样本集Xi=[x1，x2，…，xm]T，y=[y1，y2，yn]T与超参数向量Θk不断更新，因此高斯过程模型也随着实际系统的变化而不断更新，这种特性正好符合此类受噪声干扰系统不断变化的要求，较准确地预测了NCO的值，以决策下一时刻的最优控制率.

4 实例研究 4.1 问题描述

考虑一个连续搅拌的Williams-Otto反应器，如图 3所示.

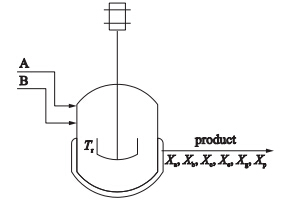图 3 Williams-Otto反应器反应示意图Fig. 3 The schematic diagram of Williams-Otto reactor
图选项

反应器发生的化学反应如下：

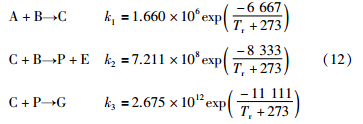
其中包括A和B两股进料，产物E和P是所需产品，C和G是副产品，操纵变量为反应器温度Tr，扰动为两股进料流量的变化，k1、 k2、 k3为反应常数. 各变量物理含义及其标称值如表 1所示.
表 1 各变量物理含义及标称值 Tab. 1 Physical meanings and nominal values of the process variables
变量名称含义标称值
Fa进料A流量4.535 kg/s
Fb进料B流量10.382 kg/s
Tr反应器温度99.55 ℃
Fr产物流量14.917 kg/s
XaA组份含量0.121 7
XbB组份含量0.378 1
XcC组份含量0.018 2
XeE组份含量0.271 1
XgG组份含量0.112 8
XpP组份含量0.097 9
J目标函数值1 179.633 7 ＄/s
表选项

选取NCO为被控变量，由于只有一个操纵变量Tr，且没有约束条件Ga，因此用Tr来进行优化操作，保证产量并使NCO为0. 而过程扰动主要来自Fa和 Fb的变化，优化操作目的是为在Fa和Fa变化的情况下最小化J. 这里，Fa和Fb的变化范围为： 3 kg/s≤Fa≤8 kg/s，9 kg/s≤Fb≤12 kg/s； 操纵变量u，测量变量X，扰动变量d如式(13)描述：

过程的经济性能优化目标为收益函数(单位： ＄/s)：

其中，Xe=Φe(Tr，Fa，Fb)，Xp=Φp(Tr，Fa，Fb).

4.2 NCO建模

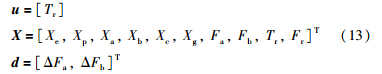
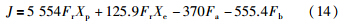
过程优化效果取决于对NCO的预测精度，这里，定义相关性函数R与时间复杂度来评价预测效果.

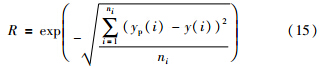
对NCO全局离线建模可得到全局近似估计模型c1(线性模型)[11]和c2(非线性模型)[12]，与不同样本集D的高斯过程模型进行相关性与时间复杂度对比，结果如表 2所示.

表 2 不同模型相关性和时间复杂度对比 Tab. 2 Comparisons in terms of relevance and time complexity among different models
模型类型相关性R时间复杂度ο
c10.817 2离线
c20.845 9离线
n=200.835 9ο(203/6)
n=300.908 4ο(303/6)
n=800.955 6ο(803/6)
n=1600.988 9ο(1603/6)
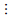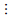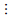
n较大≈1ο(n3/6)
表选项

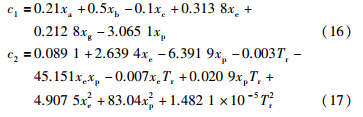
可以看到，模型1与c2的相关性分别为0.817 2和0.845 9，总体来说没有高斯过程模型相关性好，在高斯过程模型中样本集越大，相关程度越高，但是时间复杂度呈幂级数上升，影响迭代速率. 综合考虑以上两方面的因素，在仿真研究中，高斯过程模型样本集取n=125.

由于只有一个操纵变量Tr，且没有约束条件Ga，由式(2)可简化NCO为dJ/dTr. 选取dJ/dTr为被控变量，并取设定点为0.

样本数据如下方法获取： 3 kg/s≤Fa≤8 kg/s，9 kg/s≤Fb≤12 kg/s，Tr-99.55/99.55≤5％的范围内各取4等分点，分别在这53种情况下采取摄动法获得稳态X和dJ/dTr的值，形成125组样本，如图 1所示方法，离线训练得到高斯过程初始模型.

4.3 仿真实验

采用Matlab Simulink平台进行仿真实验，建立如图 2所示的基于高斯过程模型的NCO控制系统. 由于此生产过程存在滞后环节，采用PI控制器，系统工作于闭环状态. 高斯过程模型的动态更新时间应大于仿真过程相应时间，以保证新样本采集的完整性，此设定为20 s更新1次.

在初始时刻，Fa和Fb处于标称点，在t=500 s时刻Fb阶跃变化为12.000，在t=1 000 s时刻Fa阶跃变化为3.500，在t=1 500 s时刻Fa阶跃变化为5.000、 Fb阶跃变化为9.000，如图 4所示，理论上与之对应的收益函数标称值J如表 3所示.

表 3 不同扰动下的收益函数最优值 Tab. 3 Optimal values of profit functions under different disturbances
扰动1(Fa)扰动2(Fb)标称值J(＄/s)
4.53510.3821 179.656
4.53512.0001 131.321
3.50012.000807.319
5.0009.0001 046.930
表选项
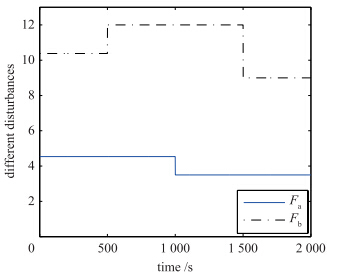图 4 扰动变化曲线Fig. 4 Curves of disturbances
图选项

优化效果如图 5所示，由于全局模型c1为线性模型，在全局近似估计中局部误差较明显，当有扰动产生时其在控制性能上存在缺失，稳态误差比较显著. 而全局模型c2为非线性模型，在优化过程中振幅程度比较大，过程不够平稳，性能损失较大. 仿真曲线表明由于高斯过程模型在优化控制过程中，随着生产过程的变化而不断更新，准确地预测出NCO的值，PI控制器根据当前NCO的值，给予系统下一时刻的最优控制率，继而快速且平稳地克服了扰动，这样长期的更大且平稳的生产性能指标意味着更高的经济效益.

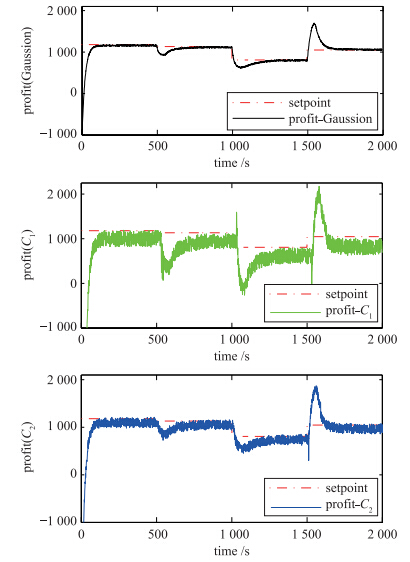图 5 优化效果对比曲线Fig. 5 Comparison curves of the optimization results
图选项

NCO在线观测曲线(如图 6所示)表明，由于高斯过程模型快速且准确地预测NCO的值，并通过PI控制器使其快速回到0附近，以实现生产过程对经济性能最优值的跟踪，而模型c1、 c2震荡明显且持续时间较长，这也是造成经济性能不佳的最主要原因.

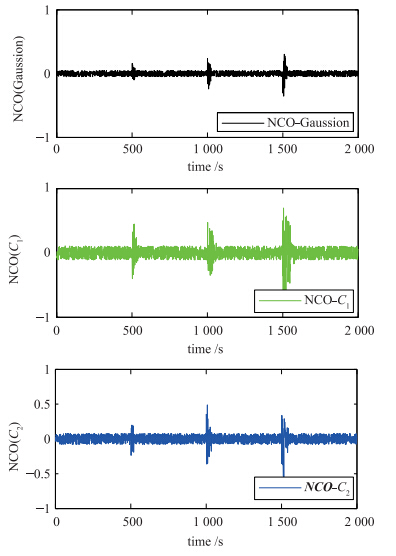图 6 3种策略的NCO在线近似曲线Fig. 6 NCO on-line approximate curves of the three strategies
图选项

为进一步说明优化控制效果，又定义了如下损失函数：

其中，Lu(u，d)是被控变量在设定点时的生产过程实际收益函数值与此时理论上的最优值之差，收益函数的损失来源于设定值误差和实施误差.

使用积分器对3种不同的NCO近似策略的损失进行了积分运算，结果显示，在2 000 s的操作时间范围内，全局近似估计模型c1的总损失值为85 689.897＄，模型c2总损失值为71 543.342＄，高斯过程模型总损失值为58 792.113＄，由此可见，随着NCO在线预测更加及时与准确，生产过程的经济性能得到了显著提高. 5 结论

结合自主优化控制思想，选取NCO作为控制系统的实现目标，可以从结构设计角度有效地提高生产过程的经济性能. 本文提出了一种在线实时预测与实现NCO的方法. 通过合理的样本集选取，离线建立高斯过程初始模型，根据生产过程数据，在线不断获得新的训练样本，动态更新高斯过程模型，实时较准确地预测了NCO的值，在有扰动产生时很好地跟踪了生产过程的经济性能最优值. 仿真研究表明该方法可行性强、 预测及时且精度高，实现了对过程经济性能的优化. 后续工作将进一步完善与拓展此类方法，并应用于复杂的工业过程.

参考文献
[1] Manum H, Skogestad S. Self-optimizing control with active set changes[J]. Journal of Process Control, 2012, 22(5): 873-883.
[2] Yelchuru R, Skogestad S. Convex formulations for optimal selection of controlled variables and measurements using mixed integer quadratic programming[J]. Journal of Process Control, 2012, 22(6): 995-1007.
[3] Sequeira S, Graells M, Puigjaner L. On-line process optimization: Parameter tuning for the real time evolution (RTE) approach[J]. Computers & Chemical Engineering, 2004, 28(2): 343-349.
[4] Gao W H, Sebastian E. Iterative set-point optimization of batch chromatographia[J]. Computer & Chemical Engineering, 2004, 18(3): 661-666.
[5] Skogestad S. Plantwide control: the search for the self-optimizing control structure[J]. Journal of Process Control, 2000, 10(5): 487-507.
[6] Bonvin D, Srinivasan B. Optimal grade transition for polyethylene reactors via NCO tracking[J]. Chemical Engineering Research and Design, 2005, 83(6): 692-697.
[7] Cao Y, Kariwala V. Bidirectional branch and bound for controlled variable selection, Part Ⅱ: Exact local method for self-optimizing control[J]. Computers & Chemical Engineering, 2009, 33(8): 1402-1412.
[8] Francois G, Srinivasan B. Use of measurement for enforcing the necessary conditions of optimality in the presence of constraints and uncertainty[J]. Journal of Process Control, 2005, 15(6): 701-712.
[9] Bonvin D, Srinivasan B. On the role of the necessary conditions of optimality in structuring dynamic real-time optimization schemes[J]. Computers & Chemical Engineering, 2013, 51(3): 172-180.
[10] Mohammad H R, Nasser S. Hierarchical optimal control of large-scale nonlinear chemical processes[J]. ISA Transactions, 2009, 48(2): 38-47.
[11] Jaschke J, Skogestad S. NCO tracking and self-optimizing control in the context of real-time optimization[J]. Journal of Process Control, 2011, 21(10): 1407-1416.
[12] Ye L, Li Y, Song Z. New approach for constructing controlled variables for chemical processes[J]. Chinese Journal of Chemical Engineering, 2011, 62(8): 2221-2226.
[13] Yip W S, Marlin T S. The effect of model fidelity on real-time optimization performance[J]. Computers & Chemical Engineering, 2004, 28(2): 267-280.
[14] Panahi M, Skogestad S. Economically efficient operation of CO2 capturing process Part Ⅰ: Self-optimizing procedure for selecting the best controlled variables[J]. Chemical Engineering and Processing, 2011, 50(3): 247-253.
[15] Hu W, Umar L, Xiao G. Local self-optimizing control of constrained processes[J]. Journal of Process Control, 2012, 22(2): 488-493.
[16] Rasmussen C E, Christopher K I. Gaussian processes for machine learning[M]. Cambridge, MS, USA: the MIT Press, 2005.
[17] Kristjan A, Jus K. Nonlinear predictive control for models with local information and uncertainties[J]. Transactions of the Institute of Measurement and Control, 2008, 30(5): 371-396.
[18] Bojan L, Kocijan J. Predictive control of a gas-liquid separation plant based on a Gaussian process model[J]. Computers & Chemical Engineering, 2007, 31(3): 142-152.
[19] Kocijan J, Murray-Smith R. Gaussian process model identification: A process engineering case study[J]. Systems Science, 2008, 34(3): 31-38.
[20] Azman K, Kocijan J. Dynamical systems identification using Gaussian process models with incorporated local models[J]. Engineering Applications of Artificial Intelligence, 2011, 24(2): 398-408."
"http://dx.doi.org/10.13976/j.cnki.xk.2015.0449"
中国科学院主管，中国科学院沈阳自动化研究所、中国自动化学会共同主办。
0

文章信息

沈俊鹏, 黄静雯, 李宏光, 刘操
SHEN Junpeng, HUANG Jingwen, LI Hongguang, LIU Cao
面向过程经济性能优化的最优性条件在线预测与实现
An On-line Prediction and Implementation of Necessary Conditions of Optimality towards Process Economic Optimization
信息与控制, 2015, 44(4): 449-454.
INFORMATION AND CONTROL, 2015, 44(4): 449-454.
http://dx.doi.org/10.13976/j.cnki.xk.2015.0449

文章历史

收稿日期：2014-08-15
录用日期：2014-11-10
修回日期：2014-12-29

工作空间