1 Introduction
A networked control system (NCS) is a control system in which the control loop is closed over communication networks. In contrast to traditional control systems whose components are usually connected via point-to-point wiring,an NCS is a flexible architecture with the advantages of low cost,and simple installation and maintenance. However,the generally existing transmission delays and transmission intervals often degrade the performance of the NCS and even cause instability[1, 2, 3, 4, 5, 6, 7, 8]. Note that an NCS with time-varying transmission delays and intervals is also deemed as a sampled-data system under variable sampling with additional transmission delays[3].
In existing literatures,three main approaches are proposed for the analysis and the synthesis of NCSs with time-varying transmission delays and intervals:
The first one is a discrete-time modeling approach,which discretizes the continuous-time NCSs and transforms the effects of transmission delays and intervals into its model parameters. However,this approach may be inappropriate for NCSs with parametric uncertainties or external disturbances[9, 10, 11].
The second one is an input-delay approach,which represents the NCSs as a continuous-time system with a delayed control input[12, 13, 14, 15]. The Lyapunov-Krasovskii methods have been extensively applied to the NCSs along with various techniques estimating cross-product integral terms,such as free-weighting matrix technique[12, 13, 14, 16, 17, 18],Jensen′s inequality based technique[15],and so on. The conservatism of the derived results depends on the selected Lyapunov-Krasovskii functionals and the estimation techniques for cross-product integral terms. It is known that the input-delay approach is very conservative for the NCSs with time-varying transmission delays and intervals when the input delays are taken as an uncertain bounded process ignoring the time derivatives of the input delays[12, 13, 14, 15]. Recently,input-delay approach has been revised by scaled small gain theorem[19] and input-output approach[20, 21] which exploit distributed-delay operators to derive less conservative results for NCSs with only variable sampling or transmission intervals. But considerable room is left for further improvement in the results.
The third one is an impulsive-model approach which models the NCSs as an impulsive system[4, 6, 22]. For the NCSs with only variable sampling or transmission intervals,a discontinuous Lyapunov functional method combined with the free-weighting matrix technique is proposed to improve the existing results by additionally exploiting the time derivatives of input delays and the impulsive effects of feedback signals and input delays[22],which motivates a novel time-dependent Lyapunov functional method[23] and looped functional methods[24, 25] to improve the existing results greatly in the framework of the input-delay approach. However,for NCSs with time-varying transmission delays and intervals,the existing results are still very conservative due to the lack of an appropriate Lyapunov functional to efficiently characterize the system behavior of the NCSs based on the time derivatives of input delays and the impulsive effects of input delays and feedback signals[3, 26, 27, 28].
In this paper,we consider to derive new stability criteria for an NCS with time-varying transmission delays and intervals based on a new discontinuous Lyapunov functional method in the framework of input-delay approach. Note that the NCSs with transmission delays and intervals have been addressed based on discontinuous Lyapunov functional methods in [3, 26, 27, 28]. For a control signal performed on the zero-order holder (ZOH),the round-trip transmission delay is taken as a component of the input delays in [3, 26, 27, 28]. In this paper,the evolution of transmission delays is additionally taken into account by describing the accumulating transmission delays as the potential input delays before the corresponding control signal is imposed on the ZOH. Meanwhile,the actual input delays are related to the time when the corresponding control signal is performed on the ZOH,and take the round-trip transmission delay as a component as in [3, 26, 27, 28]. The time derivatives of the potential and actual input delays are both equal to 1. Based on these thoughts,the impulsive effects of input delays and feedback signals are revealed more fully than the ones in [3, 26, 27, 28],and are rationally treated along with the time derivatives of input delays by the new discontinuous Lyapunov functional method. This leads to the reduced conservatism in the derived stability criteria. A numerical example is presented to substantiate the advantages of our proposed method.
Notations The expression P >0 means that P is real,symmetric,and positive definite. I and 0 denote an identity matrix and a zero matrix with appropriate dimensions,respectively. The space of functions φ : [- ,0]→Rn ,which are absolutely continuous functions on [- ,0] and have a finite lim θ→0- φ (θ) and square integrable first-order derivatives,is denoted by W with its norm as

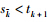 is denoted as a block matrix or vector with the component matrices or vectors in { } arranged as a column.
is denoted as a block matrix or vector with the component matrices or vectors in { } arranged as a column.
2 Problem formulation
Considering a linear system of the form:
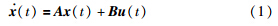
Assuming that: 1) The sensor,the controller and the ZOH are connected through communication networks. 2) Feed-back signals and control signals are transmitted in single packet,and there exist time-varying transmission delays in the channels from the sensor to the controller and from the controller to the ZOH. 3) Only new control signals are applied to updating the ZOH,and u (t)= 0 before the first updating instant of the ZOH.
In the presence of transmission delays and intervals,the networked control based on state feedback and the ZOH is given as
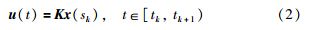
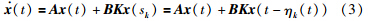
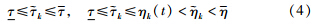
Lemma 1 [23] Let there exist positive scalars β1,β2 and a function V∶ R×W×L2[- ,0]→R such that
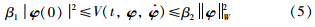
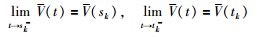
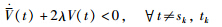
For a continuous-time process,impulsive effects mean that there are discrete-time jumps arising in the evolution of the continuous-time process. To fully reveal the impulsive effects of input delays and feedback signals in the NCS,the accumulating transmission delays are taken as the potential input delays for the associated feedback signal in this paper. Namely,for a state feedback x (sk),τk(t)=t-sk are the potential input delays for t∈[sk,tk) while ηk(t) are the actual input delays for t∈[tk,tk+1). The potential input delays τk(t) vary with a time derivative being 1 for t∈[sk,tk),which is same as the one of ηk(t) for t∈[tk,tk+1). At tk,the potential input delay is incorporated into the actual input delay ηk(tk) with a value of the round-trip transmission delay k . For t∈[tk,tk+1),the actual input delays ηk(t) coexist with at least one potential input delays 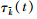 with
with 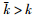 and
and 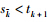 in the NCS (3). For the convenience of theoretical analysis,it is assumed in this paper that
in the NCS (3). For the convenience of theoretical analysis,it is assumed in this paper that

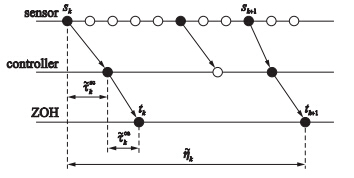 |
| Fig. 1 An example of the sequence diagram of {(sk,tk),k∈{1,2,…}} |
Based on the assumption in (6),the time interval [tk,tk+1) can be divided into two subintervals [tk,sk+1) and [sk+1,tk+1). The impulsive effects of feedback signals and input delays in the NCS are given as follows:
1) With t varying from t-k to tk and the updating of the ZOH,the actual feedback signals jump from x (sk-1) to x (sk),the actual input delays jump from ηk-1(t-k) to ηk(tk),and the potential input delays τk(t) which stop varying at t-k are incorporated into ηk(tk). Then only the actual input delays ηk(t) exist for t∈[tk,sk+1).
2) At sk+1,a new state feedback x (sk+1) is sampled and the potential input delays τk+1(t) occur. Then the actual input delays ηk(t) coexist with the potential input delays τk+1(t) for t∈[sk+1,tk+1).
3) From tk+1- to tk+1,the actual feedback signals jumps from x (sk) to x (sk+1) along with the updating of the ZOH,and the two aforementioned coexisting input delays stop increasing with the actual input delays jumping from ηk(tk+1-) to ηk+1(tk+1) and the potential input delays τk+1(tk+1-) being incorporated into ηk+1(tk+1). Then only the actual input delays ηk+1(t) exist for t∈[tk+1,sk+2).
Based on the analysis above,it is ready to propose the discontinuous Lyapunov functional. 3. 2 Construction of discontinuous Lyapunov functional
In this paper,a new discontinuous Lyapunov functional is proposed based on the impulsive effects of feedback signals and input delays and the time derivatives of input delays as follows:
For t∈[tk,sk+1),

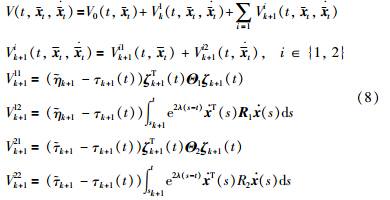
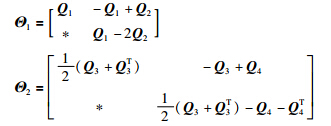
Lemma 2 For a scalar λ≥0,if there exist matrices P >0, Q 1= Q T1, Q 2= Q T2,Q 3, Q 4, R 1>0, R 2>0 with appropriate dimensions such that
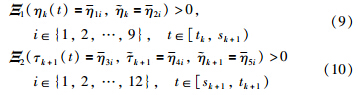
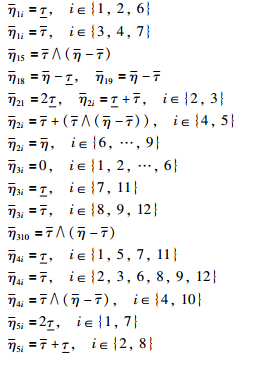

 is convex with respect to ηk(t)∈
is convex with respect to ηk(t)∈  and
and With
With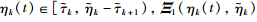 is equivalent to
is equivalent to

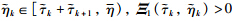 is equivalent to
is equivalent to
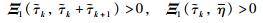
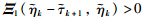 is equivalent to
is equivalent to
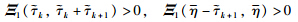
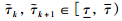 and
and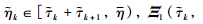
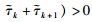 is equivalent to
is equivalent to
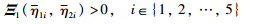
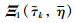 is equivalent to
is equivalent to
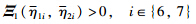
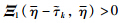 is equivalent to
is equivalent to

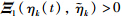 > holds if and only if (9) is feasible,which guarantees the positivity of
> holds if and only if (9) is feasible,which guarantees the positivity of 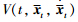 for t∈[tk,sk+1).
for t∈[tk,sk+1). 2) For t∈[sk+1,tk+1),the following inequality holds:
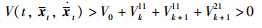
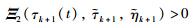
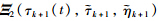 is convex with respect to
is convex with respect to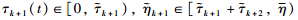 an
an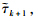
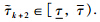 With
With 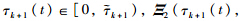
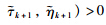 is equivalent to
is equivalent to
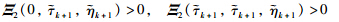
With 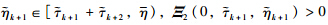 is equivalent to
is equivalent to
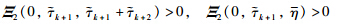
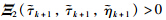 is equivalent to
is equivalent to

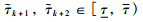 and
and 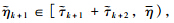
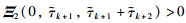 is equivalent to
is equivalent to
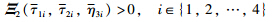
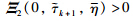 is equivalent to
is equivalent to

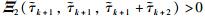 is equivalent to
is equivalent to
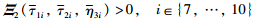
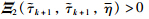 is equivalent to
is equivalent to
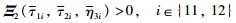
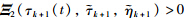 holds if and only if (10) is feasible,which guarantees the positivity of
holds if and only if (10) is feasible,which guarantees the positivity of 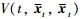 for t∈[sk+1,tk+1). The proof of Lemma 2 is completed.
for t∈[sk+1,tk+1). The proof of Lemma 2 is completed. Remark 1 The potential input delays are important to guarantee the continuity of the discontinuous Lyapunov functional in (7) and (8). As seen in (7) and (8),by exploiting the potential input delays τk(t) for t∈[sk,tk) and the actual input delays ηk(t) for t∈[tk,tk+1),the discontinuous term Vk1 is actually defined in the interval [sk,tk+1) with Vk1(sk)=0 for nonzero x (sk) and Vk1(tk+1-)=0 for nonzero x (tk+1-). If the potential input delays τk(t) are ignored for t∈[sk,tk),Vk1 can only be defined in the interval [ tk,tk+1). When k≠0 and x (sk)≠ x (tk),it follows that Vk1(tk)≠0 for nonzero x (sk) and x (tk),and Vk1(tk+1-)=0 for nonzero x (tk+1-). Then the continuity of the whole discontinuous functional will be lost. Meanwhile,by further exploiting the potential input delays τk(t) for t∈[sk,tk),the discontinuous term Vk2 defined in [sk,tk) provides more freedom for the discontinuous Lyapunov functional in (7) and (8) to characterize the behavior of the NCS,which helps to reduce the conservatism in the derived results.
Remark 2 In [3,26-28],the potential input delays are completely ignored,and the time-varying[26, 27] or constant[3, 28] round-trip transmission delays are taken as components of the actual input delays. There are no discontinuous terms Vk1 and Vk2 for t∈[sk,tk) in the Lyapunov functionals of [3,26-28]. In [3],the discontinuous terms of the Lyapunov functional are mainly based on the extended Wirtinger′s inequality. In [26],the whole Lyapunov functional is discontinuous in value as the one in [22],where the discontinuous terms are actually given as
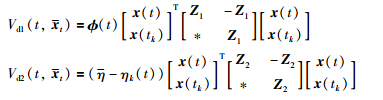
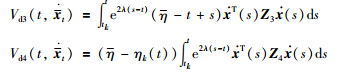
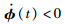 for all t≠tk. However,the discontinuous terms Vd1 and Vd2 do not directly depend on the state feedback x (sk),and the discontinuous term Vd4 is only related to the delays in [0,t-tk) which excludes the actual input delays ηk(t). These terms often result in much conservatism in the derived results. Although the term Vd3 helps to relieve this situation,it actually takes the actual input delays ηk(t) as an uncertain bounded process and ignores the time derivatives of ηk(t) as some continuous integral terms do in the Lyapunov functional of [26]. Then much room is still left for the reduction of the conservatism. In [27],the time-varying transmission delays of an event-triggered the NCS have been ignored by the discontinuous terms in the Lyapunov functional of the form:
for all t≠tk. However,the discontinuous terms Vd1 and Vd2 do not directly depend on the state feedback x (sk),and the discontinuous term Vd4 is only related to the delays in [0,t-tk) which excludes the actual input delays ηk(t). These terms often result in much conservatism in the derived results. Although the term Vd3 helps to relieve this situation,it actually takes the actual input delays ηk(t) as an uncertain bounded process and ignores the time derivatives of ηk(t) as some continuous integral terms do in the Lyapunov functional of [26]. Then much room is still left for the reduction of the conservatism. In [27],the time-varying transmission delays of an event-triggered the NCS have been ignored by the discontinuous terms in the Lyapunov functional of the form:
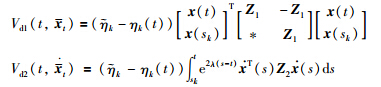
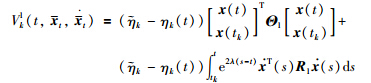
Theorem 1 Given (4) and (6),a scalar λ≥0 and the controller gain matrix K in (2),the NCS in (3) is exponentially stable with a decay rate λ,if there exist matrices P >0,Q i= Q iT(i∈{1,2}),Q i(i∈{3,4}),R i>0(i∈{1,2}),L 1j,M 1j(j∈{1,2,3}),L 2j,M 2j,N ij(i∈{1,2},j∈{1,2,3,4}) of appropriate dimensions such that (9) and (10),and

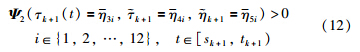
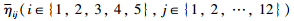 are defined as in Lemma 2,and
are defined as in Lemma 2,and
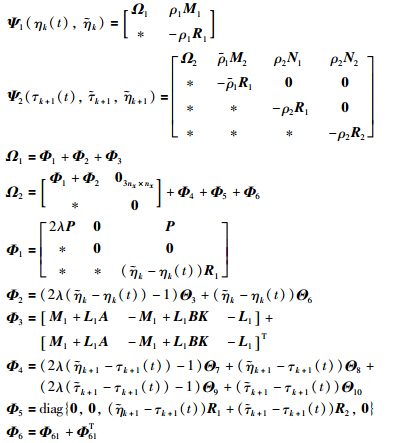

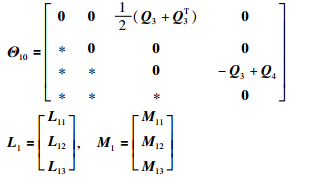
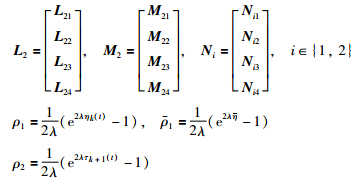
1) Along the trajectories of the closed-loop NCS in (3) for t∈[tk,sk+1),it follows that
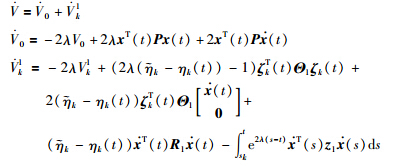
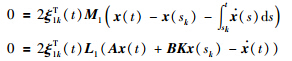
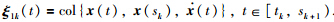 . Note that
. Note that
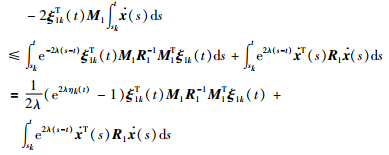
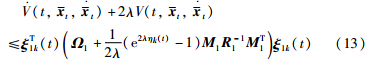
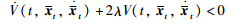
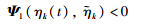
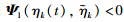 is convex with respect to ηk(t)∈
is convex with respect to ηk(t)∈ 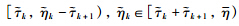 and
and 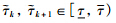 for t∈[tk,sk+1). Similar to
for t∈[tk,sk+1). Similar to 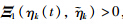 is sufficiently guaranteed by (11) for t∈[tk,sk+1).
is sufficiently guaranteed by (11) for t∈[tk,sk+1). 2) Along the trajectories of the closed-loop system (3) for t∈[sk+1,tk+1),it follows that
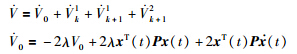
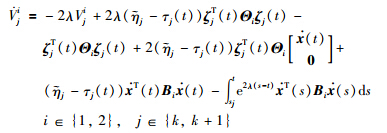
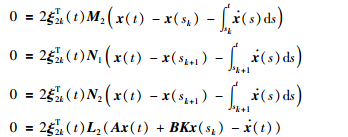
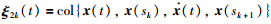 . Note that
. Note that
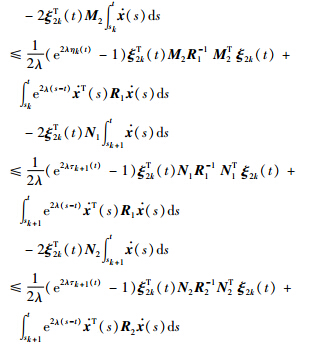

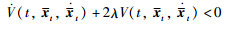
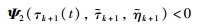
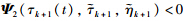 is convex with respect to
is convex with respect to 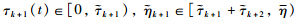 and
and 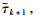
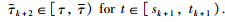 . Similar to
. Similar to 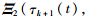
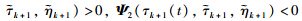 is sufficiently guaranteed by (12) for t∈[sk+1,tk+1).
is sufficiently guaranteed by (12) for t∈[sk+1,tk+1).
Based on the discussion in 1) and 2),it follows that 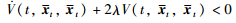 along the trajectories of the NCS in (3) for all t≠sk,tk. Then the NCS in (3) is exponentially stable according to Lemma 1. The proof of Theorem 1 is completed.
along the trajectories of the NCS in (3) for all t≠sk,tk. Then the NCS in (3) is exponentially stable according to Lemma 1. The proof of Theorem 1 is completed.
Remark 3 The conservatism of Theorem 1 mainly comes from 4 aspects: 1) The proposed discontinuous Lyapunov functional in (7) and (8) cannot perfectly characterize the system behavior of the NCS. A more advanced discontinuous Lyapunov functional is still needed to more rationally exploit the impulsive effects of input delays and feedback signals and the time derivatives of input delays. 2) The applied free weighting matrix technique is still conservative to some extent in estimating the cross-product integral terms. 3) The quantity ek2λη(t) in (14) is estimated as e2λ by 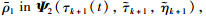 which leads to some conservatism in the derived results. If the quantity e2ληk(t) is directly taken by
which leads to some conservatism in the derived results. If the quantity e2ληk(t) is directly taken by 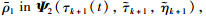 ,a larger number of LMIs will be introduced into Theorem 1 by the convexity technique. 4) There is some conservatism in (11) with respect to
,a larger number of LMIs will be introduced into Theorem 1 by the convexity technique. 4) There is some conservatism in (11) with respect to 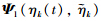 for the presence of ρ1 in
for the presence of ρ1 in 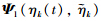 . Meanwhile,(12) is relatively conservative with respect to
. Meanwhile,(12) is relatively conservative with respect to 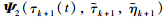 due to the existence of
due to the existence of 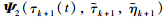 .
.
Remark 4 The computational complexities of the stability conditions of [3,26] and Theorem 1 are given in Tab. 1. The number of the decision variables in Theorem 1 is larger than the one in [3],and is smaller than the one in [26]. The number of the linear matrix inequalities (LMIs) in Theorem 1 is larger than the ones in [3, 26]. The total dimensions of the LMIs in Theorem 1 are larger than the ones in [3],and are smaller than the ones in [26]. By the applied convexity technique,the four inequalities 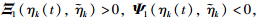
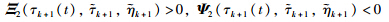 results in the 42 LMIs in Theorem 1. The reduced conservatism of Theorem 1 is related to the increased number of the LMIs.
results in the 42 LMIs in Theorem 1. The reduced conservatism of Theorem 1 is related to the increased number of the LMIs.
Based on Theorem 1,we have the following controller design method:
Theorem 2 Given (4),(6),and scalars λ≥0,σ11=1,σ1j,j∈{2,3},σ2j,j∈{1,2,3,4},the NCS in (3) with the controller gain K = YX -T is exponentially stable with a decay rate λ,if there exist matrices 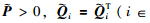
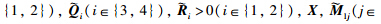
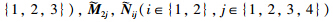 ,and Y of appropriate dimensions,such that
,and Y of appropriate dimensions,such that

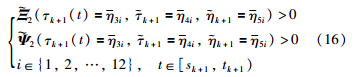
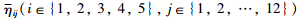 is defined as in Lemma 2,and
is defined as in Lemma 2,and 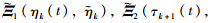
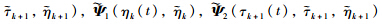 are defined as
are defined as 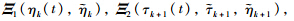
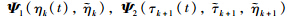 in Theorem 1,respectively,with
in Theorem 1,respectively,with 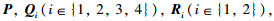
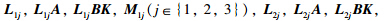
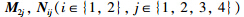 replaced by
replaced by 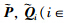
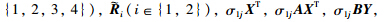
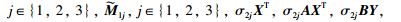
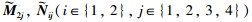 respectively.
respectively.
Proof Define L 1j=σ1j L 11(j∈{2,3}), L 2j=σ2j L 11(j∈ {1,2,3,4}). Define X = L -111, Y = KX T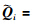 = XPX T,
= XPX T,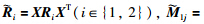
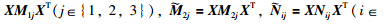 (i∈{1,2},j∈{1,2,3,4}). We have (15) and (16) from (9) and (10),and (11) and (12) by congruence transformation with diag { X ,X } and diag { X ,X ,X },and diag { X ,X ,X } and diag { X ,X ,X ,X },respectively. For more details of the congruence transformation,please refer to [12-13]. The proof of Theorem 2 is completed.
4 A numerical example
(i∈{1,2},j∈{1,2,3,4}). We have (15) and (16) from (9) and (10),and (11) and (12) by congruence transformation with diag { X ,X } and diag { X ,X ,X },and diag { X ,X ,X } and diag { X ,X ,X ,X },respectively. For more details of the congruence transformation,please refer to [12-13]. The proof of Theorem 2 is completed.
4 A numerical example
Example 1 Considering the following system[22]:
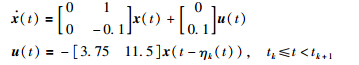
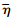 computed by Theorem 1 and the existing methods under different
computed by Theorem 1 and the existing methods under different 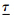 and
and 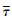 ,where
,where 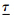 =
= 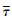 means that the transmission delays are constant. It is seen from Tab. 2 that: a) For a same
means that the transmission delays are constant. It is seen from Tab. 2 that: a) For a same 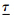 ,a larger
,a larger 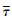 leads to a larger maximal value of
leads to a larger maximal value of 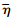 ; b) The maximal values of
; b) The maximal values of 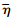 decrease with the increase of
decrease with the increase of 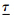 ; c) Our numerical results are all better than those of [22],[26],[3] and [28]. So our proposed approach is advantageous over the existing ones.
; c) Our numerical results are all better than those of [22],[26],[3] and [28]. So our proposed approach is advantageous over the existing ones.
In this paper,a new stability criteria are derived for an NCS with time-varying transmission delays and intervals. The evolution of transmission delays is additionally taken into account by describing the accumulating transmission delays as the potential input delays before the corresponding control signal is imposed on the ZOH. A new discontinuous Lyapunov functional method is proposed to rationally consider the impulsive effects of input delays and feedback signals and the time derivatives of input delays,which leads to less conservatism in the derived results. A numerical example is presented to substantiate the advantage of the proposed approach.
| [1] | Zhang W, Branicky M S, Phillips S M. Stability of networked control systems[J]. IEEE Control System Magazine, 2001, 21(1): 84-99. |
| [2] | Antsaklis P, Baillieul J. Special issue on technology of networked control systems[J]. Proceedings of the IEEE, 2007, 95(1): 5-8. |
| [3] | Liu K, Fridman E. Wirtinger's inequality and Lyapunov-based sampled-data stabilization[J]. Automatica, 2012, 48(1): 102-108. |
| [4] | Heemels W, Teel A, van de Wouw N, et al. Networked control systems with communication constraints: Tradeoffs between transmission intervals, delays and performance[J]. IEEE Transactions on Automatic Control, 2010, 55(8): 1781-1796. |
| [5] | Donkers M C F, Heelmels W P M H, van de Wouw N, et al. Stability analysis of networked control systems using a switched linear systems approach[J]. IEEE Transactions on Automatic Control, 2011, 56(9): 2101-2115. |
| [6] | Donkers M C F, Heelmels W P M H. Output-based event-triggered control with guaranteed L∞-gain and improved and decentralized event-triggering[J]. IEEE Transactions on Automatic Control, 2012, 57(6): 1521-1526. |
| [7] | Heelmels W P M H, Donkers M C F, Teel A R. Periodic event-triggered control for linear systems[J]. IEEE Transactions on Automatic Control, 2013, 58(4): 847-861. |
| [8] | Karafyllis I, Krstic M. Nonlinear stabilization under sampled and delayed measurements, and with inputs subject to delay and zero-order hold[J]. IEEE Transactions on Automatic Control, 2012, 57(5): 1141-1154. |
| [9] | Suh Y S. Stability and stabilization of nonuniform sampling sys-tems[J]. Automatica, 2008, 44(12): 3222-3226. |
| [10] | Fujioka H. A discrete-time approach to stability analysis of systems with aperiodic sample-and-hold devices[J]. IEEE Transactions on Automatic Control, 2009, 54(10): 2440-2445. |
| [11] | Oishi Y, Fujioka H. Stability and stabilization of a periodic sampled-data control systems using robust linear matrix inequalities[J]. Automatica, 2010, 46(10): 1327-1333. |
| [12] | Yue D, Han Q L, Peng C. State feedback controller design of networked control systems[J]. IEEE Transactions on Circuits and Systems-II: Express Briefs, 2004, 51(11): 640-644. |
| [13] | Tang B, Liu G P, Gui W H. Improvement of state feedback controller design for networked control systems[J]. IEEE Transactions on Cir-cuits and Systems-II: Express Briefs, 2008, 55(5): 464-468. |
| [14] | Gao H J, Chen T W, Lam J. A new delay system approach to network-based control[J]. Automatica, 2008, 44(1): 39-52. |
| [15] | Jiang X, Han Q L, Liu S, et al. A new H∞stabilization criterion for networked control systems[J]. IEEE Transactions on Automatic Control, 2008, 53(4): 1025-1032. |
| [16] | He Y, Wu M, She J H, et al. Delay-dependent robust stability criteria for uncertain neutral systems with mixed delays[J]. Systems & Control Letters, 2004, 51(1): 57-65. |
| [17] | Wu M, He Y, She J H. New delay-dependent stability criteria and stabilizing method for neutral systems[J]. IEEE Transactions on Automatic Control, 2004, 49(12): 2266-2271. |
| [18] | He Y, Wu M, She J H. Improved bounded-real-lemma representation and H-inf control of systems with polytopic uncertainties[J]. IEEE Transactions on Circuits and Systems-II: Express Briefs, 2005, 52(7): 380-383. |
| [19] | Mirkin L. Some remarks on the use of time-varying delay to model sample-and-hold circuits[J]. IEEE Transactions on Automatic Control, 2007, 52(6): 1109-1112. |
| [20] | Fujioka H. Stability analysis of systems with a periodic sample-and-hold devices[J]. Automatica, 2009, 45(3): 771-775. |
| [21] | Liu K, Suplin V, Fridman E. Stability of linear systems with general sawtooth delay[J]. IMA Journal of Mathematical Control and Information, 2010, 27(4): 419-436. |
| [22] | Naghshtabrizi P, Hespanha J P, Teel A R. Exponential stability of impulsive systems with application to uncertain sampled-data systems[J]. Systems & Control Letters, 2008, 57(5): 378-385. |
| [23] | Fridman E. A refined input delay approach to sampled-data control[J]. Automatica, 2010, 46(2): 421-427. |
| [24] | Seuret A. A novel stability analysis of linear systems under asynchronous samplings[J]. Automatica, 2012, 48(1): 177-182. |
| [25] | Briat C, Seuret A. A looped-functional approach for robust stability analysis of linear impulsive systems[J]. Systems & Control Letters, 2012, 61(10): 980-988,. |
| [26] | Chen W H, Zheng W X. Input-to-state stability for networked control systems via an improved impulsive system approach[J]. Automatica, 2011, 47(4): 789-796. |
| [27] | Yue D, Tian E, Han Q L. A delay system method for designing event-triggered controllers of networked control systems[J]. IEEE Transactions on Automatic Control, 2013, 58(2): 475-481. |
| [28] | Peng C, Han Q L. A novel event-triggered transmission scheme and L2 control co-design for sampled-data control systems[J]. IEEE Transactions on Automatic Control, 2013, 58(10): 2620-2626." |



