文章快速检索  
  高级检索
引用本文
高闪, 梅劲松. 输入非线性系统的执行器故障容错控制[J]. 信息与控制, 2015, 44(4): 463-468
GAO Shan, MEI Jingsong. Fault Tolerant Control of Actuator Faults for Input Nonlinear Systems[J]. INFORMATION AND CONTROL, 2015, 44(4): 463-468.
输入非线性系统的执行器故障容错控制
高闪, 梅劲松    
南京航空航天大学自动化学院, 江苏 南京 210016
收稿日期: 2014-07-21; 录用日期: 2014-11-06; 修回日期: 2015-03-28
基金项目: 中央高校基本科研业务费专项资金资助项目（NE2014202）.
作者简介: 梅劲松（1967-），男，博士，副研究员．研究领域为无人机飞行控制技术，自动化控制与检测技术，超声探伤检测技术．
通讯作者: 高闪（1990-），女，硕士生．研究领域为非线性系统执行器故障的容错控制．gs@nuaa.edu.cn
摘要: 研究一类具有模型不确定性和外界干扰的非线性系统的执行器故障容错控制问题，其中控制输入是由一个带死区、饱和的非线性函数描述．针对执行器故障未知且在未知时间发生的特点，采用自适应滑模变结构技术跟踪控制，并设计基于故障补偿的容错控制算法以保证故障系统的稳定性．最后，通过一个实例来验证该方法的有效性．
关键词: 死区、饱和/非线性     容错控制     自适应滑模     跟踪控制    
Fault Tolerant Control of Actuator Faults for Input Nonlinear Systems
GAO Shan , MEI Jingsong     
College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016 China
Abstract: We studied the fault-tolerant control problem of actuator faults for a class of nonlinear systems with model uncertainties and external disturbances, where in the control inputs were described by nonlinear functions subject to actuator dead zone and saturation. For problems where in the actuator faults and the times of their occurrence were unknown, we designed a tracking control method based on an adaptive sliding mode variable structure technique and a fault-tolerant control algorithm based on fault compensation to guarantee the stability of the faulty systems. An example is demonstrated to verify the effectiveness of the method.
Key words:
dead-zone & saturation/nonlinearity     fault tolerant control     adaptive sliding     tracking control    

1 引言

安全问题是设计飞行器时考虑的必要因素. 随着计算机和控制理论的发展，系统安全引发出了一个重要的领域： 容错控制. 容错控制主要是指在发生故障时，系统仍能保证其稳定性性能[1, 2, 3, 4, 5]. 在控制系统中，故障按部件划分主要有执行器故障、 传感器故障、 控制器故障和被控对象故障，其中执行器故障和传感器故障发生较多. 由于执行器故障往往危及整个系统的控制策略，因此对执行器的可靠性要求很高，对其进行容错控制就具有重要的现实意义. 本文考虑执行器常见的3种故障： 失效、 损伤和卡死. 其中执行器失效故障和卡死故障会影响系统的结构，故容错控制器的设计并不容易实现.

到目前为止，有关线性系统的执行器故障容错控制研究的成果相对比较多. 文[6]针对执行器卡死故障，提出了基于迭代学习观测器的容错控制方法； 文[7]提出了一种满足Lipschitz条件非线性系统执行器故障的主动容错控制方法； 文[8]针对执行器故障提出一种集成故障检测、 诊断和故障重构的控制系统. 而现实中非线性系统的存在更为广泛，这促使我们研究非线性系统的容错控制问题. 目前处理非线性系统执行器失效故障主要有基于非线性H∞控制和基于变结构控制2种方法. 本文主要针对输入非线性系统采用自适应滑模变结构控制对未知的执行器故障进行容错控制. 由于滑模控制对参数不确定和外部扰动均具有良好的鲁棒性，因此被认为是作为控制不确定系统的一种强有力理论. 从理论角度，在一定意义上，由于滑动模态可以按需要设计，而且系统的滑模运动对控制对象的参数变化及外界干扰无关，因此滑模变结构控制系统的鲁棒性要比一般常规的连续系统强[9, 10]. 而将自适应控制与滑模变结构控制有机结合是一种新型的解决参数不确定或时变参数系统控制问题的控制策略.

实际的执行机构往往存在一些实际物理约束，比如输出饱和特性. 这种非线性的影响在实现过程中是不可忽略的，它的存在不但降低了系统的性能，甚至使系统出现不稳定特性[11]. 这些物理约束导致传统的线性函数不能表示出执行器的特点. 例如，卫星执行器的动量轮具有非线性、 死区和饱和特性. 非线性输入系统的控制问题已越来越受关注，如文[12, 13, 14]提出用连续低增益积分控制方法对非线性输入系统的常值参考信号进行跟踪. 文[15]给出了在控制饱和度下非线性离散系统稳定的一些结果，这些饱和度建模为非线性死区且满足改进的扇区条件.

本文针对一类非线性系统执行器故障提出了一种新的容错控制方法. 考虑到执行器的特点，系统的输入信号用带死区的非线性描述. 基于滑模和自适应技术，设计容错控制律保证故障系统的稳定. 并将其应用到F-16飞机执行器故障跟踪控制问题中，以此来证明该方法的可实现性和应用性.

2 系统描述

考虑具有非线性死区、 饱和特性输入函数的线性时不变系统：

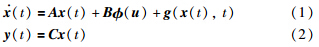
其中，x∈Rn表示系统的状态； u∈Rm表示系统的输入； y∈Rr表示可测量的输出信号； g(x(t)，t)表示外界对系统的干扰； A、 B、 C表示适当维数的实常数矩阵，其中(A，C)是可观测对，(A，B)是可控对；φ(u)=[φ(u1)，φ(u2)，…，φ(um)]T∈Rm是带有死区、 饱和特性的非线性输入函数向量.

φ(u)函数满足以下假设，其中·表示欧拉范数.

假设1(文[12]) 具有非线性输入函数φ(u)的控制信号u(u)受饱和值umax和死区值u0的约束可表示为

进一步，引入文[12]的函数χ(·)可将式(3)改写为

其中，

式中，μi是定常数，满足μi>∈｛0，1｝. 对于i=1，2，…，m，有0<μi≤χi(ui-u0)≤1. 根据文[16]可知执行器故障u(t)可描述为

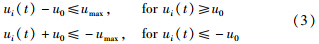
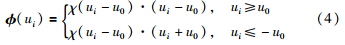
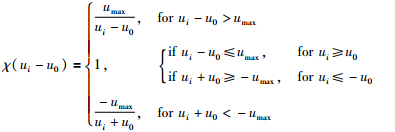
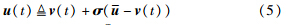
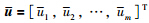其中，v(t)=[v1，v2，…，vm]T∈Rm是实控制输入向量，是故障执行器向量. 根据文[16]，定义为

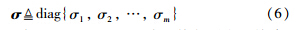
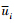其中，σi∈｛0，1｝(i=1，2，…，m)表示执行器发生故障. 当第i个执行器发生故障时σi=1，这时ui(t)=； 否则σi=0. 故障系统(1)可转化为

其中，φ(v)=[φ1(v1)，φ2(v2)，…，φm(vm)]T∈Rm.

注1 式(7)描述的执行器故障系统可写为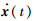=Ax(t)+Bφ(v)+Ef(t)+g(x(t)，t)，其中.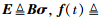

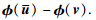假设2(文[16]) (A，B)是已知稳定的，且存在非空的故障模式集合Σ，满足

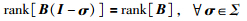
注2 假设2表明故障容错控制器的解存在，且能调节可能的执行器故障.

假设3(文[13]) 存在非负常数l1，l2使得

下面讨论具有非线性输入的故障系统跟踪问题. 期望轨迹由下面的模型描述：

其中，xm(t)∈Rn是所期望的状态轨迹，ym(t)是期望的输出轨迹，rd(t)∈Rmd是参考输入，Am和Bm是适当位数的实常数矩阵. 定义跟踪误差为： e(t)=x(t)-xm(t)，得到误差动态系统如下：

3 容错控制器的设计

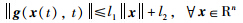
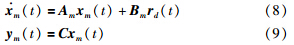
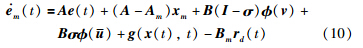
采用滑模和自适应控制技术构建容错控制器. 考虑到输入信号的非线性和死区性，滑模方法用于容错控制器的补偿设计. 首先，线性滑模面设计如下：

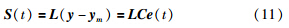
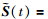
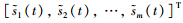其中，S(t)=[s1(t)，s2(t)，…，sm(t)]T是滑模面向量，L∈Rm×p是特定的矩阵使得矩阵LCB式非奇异. 设=BTCTLTS(t)，容错控制律设计如下：

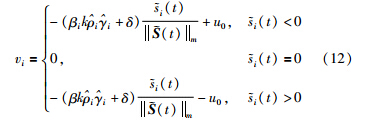
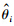其中，δ=+k1||xm||-k2||rd||+k3||x||+k4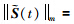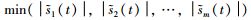， k=||(CB)-1CA||， k1=||(CB)-1C(A-Am)||， k2=||(CB)-1CBm||， k3=||(CB)-1Cl1||， k4=||(CB)-1Cl2||， β>1，参数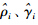和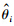的选择满足如下线性微分方程：

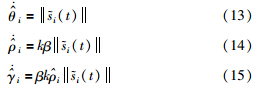
式中，i=1，…，m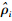，(0)=0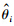，(0)=0，(0)=γ0. γ0为的有界正初始值.

引理1(文[17]) 对于所有满足假设1的非线性输入φ(u)控制律(12)满足：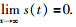

定理1 在假设1、 2下，控制律(12)的参数由式(13)～式(15)给出，可使得故障系统(7)稳定，即满足limx→∞ s(t)=0.

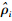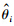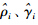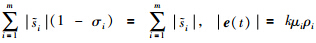证明 根据假设2，对于σ∈Σ存在、 、 满足等式和.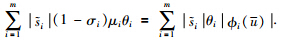

构造李亚普诺夫函数：

对李亚普诺夫函数微分：

引入引理1(16)，可得：

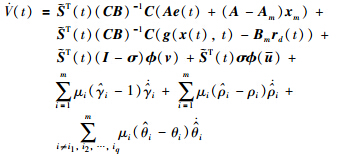
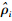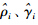参数、 和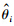的选择满足自适应律式(13)～式(15)，可得：

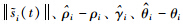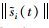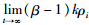
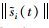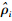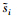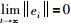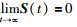不等式(18)表示的稳定性，和的一致有界性. 根据Barbalat引理(文[18])可得， =0. 因为||si(t)||和是函数ei的估计值，并且也是ei的一种函数. 因此，可得到，即证毕.

注3 在定理1中，参数k1||xm||，k2||rd||和参考模型实现轨迹跟踪相关. 这些参数初始值的选择基于其有效性. θi值+和系统的故障有关，当没有故障发生时值设为0. ρi是关于系统的状态，可以选择状态的初始值和最终值. γi是可调参数，可设为0.

4 仿真例子

为了说明文中所提出的控制方法的有效性，将所提方法用于AFTI/F-16飞机的纵向运动学模型中[19]. 对应于一些限制条件，仿真时初始值选取： 高度为8 000 ft，速度为700 ft/s，考虑机翼水平稳态飞行的状态，模型线性化为

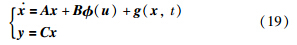
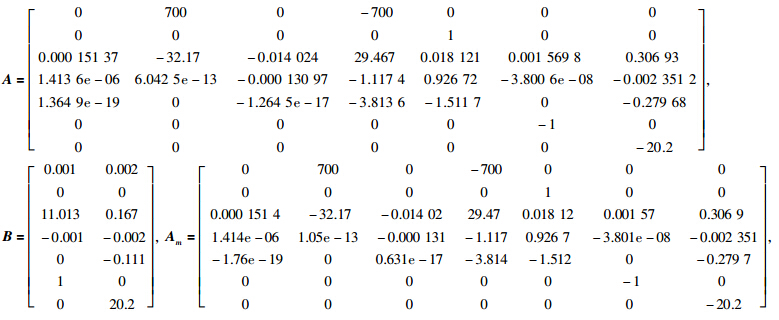
其中，x=[h，θ，V，α，q，δth，δe]T， u=[δth， δe]T，y=[V，α，θ，q]T. h为飞行高度，V为速度，α为迎角，θ 为俯仰角，q为俯仰角速度，δth为油门杆操纵量，δe为升降舵偏转角. φ(u)是非线性输入信号，且死区值为0.5. 参考输入rd=[5 000，-1]T，g(x，t)=[l1xesin x1+l2sin x2，l1xecos x1+l2cos x2]T，l1=0.063 1，l2=0.83，Bm= B，Cm= C. 仿真实例中所采用的矩阵 A，B，C， Am的值为

在文[20]中，飞机在小迎角飞行时，δe=[-25°，25°]T，δth-[1 000，19 000]T lb，在上面描述的初始条件下线性化模型时有δth=3 126.792 9 lb，α=0.970 94°，δe=-1.624 2°. 考虑实际飞行时气流的扰动，模拟时加入4.5°的迎角干扰. 根据定理1，可以计算出β=1.03，k=121 376.192，k1=197.551 5，k2=1，k3=52 776，k4=1 716 633.790 4. 在这次研究中考虑3类执行器故障类型： 失效，损伤和卡死. 如表 1所示，分别通过以下3种情况，综合考虑验证所设计的控制律的有效性.

表 1 执行器故障 Tab. 1 Actuator faults
情况(case)油门开度(δth)升降舵(δe)
情况1损失50％损失50％
情况2无故障损伤
情况3卡死损失70％
表选项

情况1： 执行器故障u(t)定义为

它表示在第3 s后，δth和δe均损失50％，仿真结果如图 1所示.

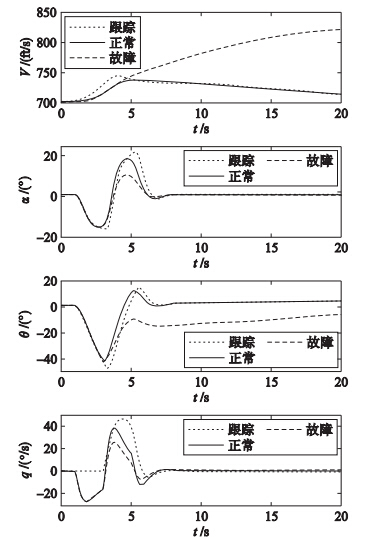图 1 系统状态(情况1)Fig. 1 The system states (case 1)
图选项

情况2： 执行器故障u(t)定义为

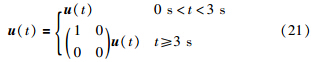
它表示δth没有发生故障，δe在第3 s后发生损伤，仿真结果如图 2所示.

图 2 系统状态(情况2)Fig. 2 The system states (case 2)
图选项

情况3： 执行器故障u(t)定义为

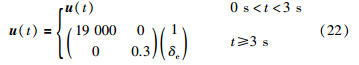
它表示在第3 s后，δth卡死在额定值，即取最高值δth=19 000 lb，δe损失70％，仿真结果如图 3所示.
图 3 系统状态(情况3)Fig. 3 The system states (case 3)
图选项

仿真结果表明，本文所设计的容错控制对模型不确定 性和外界干扰等未知信号有较强的鲁棒性. 同时能够及 时准确地控制，执行器可能发生的故障，从而保证系统实时跟踪正常理想状态. 本文故障发生在第3 s，俯仰角θ、 迎角α和俯仰角速度q无论在失效、 损伤还是卡死的情况下均能在第7 s左右很好地跟踪正常系统，且速度V在失效的状态下能快速地回到正常位置．而对于卡死和损伤，速度的修复相对要缓慢一些，但在第10 s后能恢复正常状态. 一般相隔在7 s左右都能满足实际操作的要求.

5 总结

本文研究一类输入具有死区、 饱和非线性特性的系统执行器故障的容错控制问题. 在假设执行器故障可修复的条件下，采用滑模和自适应控制相结合的技术设计容错控制律. 该控制律能使系统在发生未知执行器故障的情况下稳定跟踪期望的轨迹. 值得注意的是，为了使用该容错控制方法，系统必须有一定的冗余性. 因此如何进一步扩展该方法是今后工作的研究重点.

参考文献
[1] Blanke M, Kinnaert M, Lunze J, et al. Diagnosis and fault-tolerant control[M]. Berlin Germany: Springer-Verlag, 2003.
[2] 张新家, 戴冠中, 张建华. 容错控制系统综述[J]. 信息与控制, 1991, 20(1): 28-38. Zhang X J, Dai G Z, Zhang J H. Survey of fault tolerant control system[J]. Information and Control, 1991, 20(1): 28-38.
[3] 沈艳霞, 贺庆楠, 潘庭龙, 等. 风能转换系统T-S模糊鲁棒容错控制[J]. 信息与控制, 2013, 42(6): 750-757, 764. Shen Y X, He Q N, Pan T L, et al. T-S fuzzy robust fault-tolerant control strategy for wind energy conversion system[J]. Information and Control, 2013, 42(6): 750-757, 764.
[4] Xiao H, Wang Z D, Ji Y D, et al. Network-based fault detection for discrete-time state-delay systems: A new measurement model[J]. International Journal of Adaptive Control and Signal Processing, 2008, 22(5): 510-528.
[5] Jiang B, Staroswiecki M, Cocquempot V. Fault accommodation for a class of nonlinear dynamic systems[J]. IEEE Transactions on Automatic Control, 2006, 51(9): 1578-1583.
[6] Chen W, Jiang J. Fault-tolerant control against stuck actuator faults[J]. IEE Proceedings - Control Theory Applications, 2005, 152(2): 138-146.
[7] Gao Z W, Ding S X. Actuator fault robust estimation and fault-tolerant control for a class of nonlinear descriptor systems[J]. Automatica, 2007, 43(5): 912-920.
[8] Zhang Y M, Jiang J. Active fault-tolerant control system against partial actuator failures[J]. IEE Proceedings - Control Theory Applications, 2002, 149(1): 95-104.
[9] 刘金琨, 孙富春. 滑模变结构控制理论及其算法研究与进展[J]. 控制理论与应用, 2007, 24(3): 407-418. Liu J K, Sun F C. Research and development on theory and algorithms of sliding mode control[J]. Control Theory & Applications, 2007, 24(3): 407-418.
[10] 阎晓妹, 尚婷, 赵小国. 基于主动滑模控制的不确定分数阶混沌(超混沌)系统的延迟同步[J]. 信息与控制, 2015, 44(1): 1-7. Yan X M, Shang T, Zhao X G. Lag synchronization of uncertain fractional-order chaotic (hyperchaotic) systems using active sliding mode control[J]. Information and Control, 2015, 44(1): 1-7.
[11] 胡庆雷, 姜博严, 石忠. 基于新型终端滑模的航天器执行器故障容错姿态控制[J]. 航空学报, 2014, 35(1): 249-258. Hu Q L, Jiang B Y, Shi Z. Novel terminal sliding mode based fault tolerant attitude control for spacecraft under actuator faults[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(1): 249-258.
[12] Hu Q L, Ma G F, Xie L H. Robust and adaptive variable structure output feedback control of uncertain systems with input nonlinearity[J]. Automatica, 2008, 44(2): 552-559.
[13] Hsu K C, Wang W Y, Lin P Z. Sliding mode control for uncertain nonlinear systems with multiple inputs containing sector nonlinearities and deadzones[J]. IEEE Transactions on Systems, Man and Cybernetics, Part B: Cybernetics, 2004, 34(1): 374-380.
[14] Fliegner T, Logemann H, Ryan E P. Low-gain integral control of continuous-time linear systems subject to input and output nonlinearities[J]. Automatica, 2003, 39(3): 455-462.
[15] Castelan E B, Moreno U F, de Pieri E R. Absolute stabilization of discrete-time systems with a sector bounded nonlinearity under control saturations[C]//IEEE International Symposium on Circuits and Systems. Piscataway, NJ, USA: IEEE, 2006: 3105-3108.
[16] Liu Y, Tang X D, Tao G, et al. Adaptive compensation of aircraft actuation failures using an engine differential model[J]. IEEE Transactions on Control Systems Technology, 2008, 16(5): 971-982.
[17] Gao S, Mei J S, Cheng G J, et al. Fault-tolerant control for a class of nonlinear systems with actuator fault[C]//Chinese Automation Congress (CAC). Piscataway, NJ, USA: IEEE, 2013: 193-198.
[18] He X, Wang Z D, Zhou D H. Robust fault detection for networked systems with communication delay and data missing[J]. Automatica, 2009, 45(11): 2634-2639.
[19] Sonneveldt L. Nonlinear F-16 model description[D]. Netherland: Delft University of Technology, 2006.
[20] Stevens B L, Lewis F L. Aircraft control and simulation[M]. New York: Wiley, 1992."
"http://dx.doi.org/10.13976/j.cnki.xk.2015.0463"
中国科学院主管，中国科学院沈阳自动化研究所、中国自动化学会共同主办。
0

文章信息

高闪, 梅劲松
GAO Shan, MEI Jingsong
输入非线性系统的执行器故障容错控制
Fault Tolerant Control of Actuator Faults for Input Nonlinear Systems
信息与控制, 2015, 44(4): 463-468.
INFORMATION AND CONTROL, 2015, 44(4): 463-468.
http://dx.doi.org/10.13976/j.cnki.xk.2015.0463

文章历史

收稿日期：2014-07-21
录用日期：2014-11-06
修回日期：2015-03-28

工作空间