文章快速检索  
  高级检索
引用本文
赵石磊, 郭红, 刘宇鹏. 基于轨迹跟踪的线性时滞系统容错控制[J]. 信息与控制, 2015, 44(4): 469-473
ZHAO Shilei, GUO Hong, LIU Yupeng. Fault Tolerant Control for Linear Time-delay System Based on Trajectory Tracking[J]. INFORMATION AND CONTROL, 2015, 44(4): 469-473.
基于轨迹跟踪的线性时滞系统容错控制
赵石磊, 郭红, 刘宇鹏    
哈尔滨理工大学软件学院, 黑龙江 哈尔滨 150036
收稿日期: 2014-06-26; 录用日期: 2014-09-09; 修回日期: 2015-02-23
基金项目: 国家自然科学基金资助项目（61300115）.
作者简介: 郭红（1967-），女，硕士，副教授．研究领域为动态系统故障诊断与容错控制．
刘宇鹏（1978-），男，博士，副教授．研究领域为动态系统故障诊断与容错控制．
通讯作者: 赵石磊（1979-），男，博士，讲师．研究领域为动态系统故障诊断，容错控制，智能控制等，zhaosl@hrbust.edu.cn
摘要: 针对线性常时滞系统可能发生的执行器故障，提出了一种基于轨迹跟踪的主动容错控制方法．设计目标是通过设计容错控制率及故障观测器使故障系统状态在故障时也能够有效地跟踪参考模型状态．容错控制率的设计是为了补偿可能发生的执行器故障，比例—积分观测器则用于获取设计中需要的故障信息．在设计中，将状态估计误差、状态跟踪误差、故障估计误差及输出估计误差的动态方程组成广义系统，并通过Lypapunov-Krasovskii定理将该广义系统稳定性问题转化为线性矩阵不等式（LMI）的求解问题，进而方便地求解满足稳定性条件的观测器及控制率的增益矩阵．最后，在仿真中针对同一实例通过与经典方法的比较，证明了所提方法的有效性．
关键词: 广义系统     常时滞     容错控制     轨迹跟踪    
Fault Tolerant Control for Linear Time-delay System Based on Trajectory Tracking
ZHAO Shilei , GUO Hong, LIU Yupeng     
School of Software, Harbin University of Science and Technology, Harbin 150036, China
Abstract: With regard to the presence of actuator faults in linear constant delay systems, we propose an active fault-tolerant control scheme based on trajectory-tracking. The aim is to design a fault-tolerant control law and a fault observer to ensure the tracking of the states of faulty systems to reference models even if faults occur. The fault-tolerant control law is designed to compensate for the actuator faults; The proportional integral observer is introduced to acquire information related to the fault. The dynamics of the state, as well as the tracking, fault estimation, and output estimation errors, comprise the descriptor system. In addition, using the Lypapunov-Krasovskii theorem, the stability problem of the descriptor system can be solved easily in terms of the linear matrix inequality (LMI) to obtain the observer gain matrix and control law. Finally, a numerical example is considered to compare the tracking performance of the proposed fault-tolerant control approach with the classic approach and to illustrate the effectiveness of the proposed scheme.
Key words:
descriptor system     constant time-delay     fault tolerant control     trajectory tracking    

1 引言

现代控制系统对性能高要求的同时也增加了系统故障发生的可能性. 故障可能发生在系统的任何部位，并导致系统性能的下降甚至影响系统的稳定性. 为了提高系统的可靠性及稳定性，故障的检测、 分离及容错控制技术(fault tolerant control，FTC)在过去的几十年间一直为研究者们所关注，产生了许多研究成果[1, 2].

通常来说，容错控制技术可分为如下两大类[3, 4, 5]： (1) 被动容错： 不需要故障诊断子系统. 它是一种与鲁棒控制类似的方案，通常采用固定的控制器来确保闭环系统对特定故障的不敏感性，保持系统的稳定性，并具有一定的期望性能； (2) 主动容错： 一般需要故障诊断子系统提供故障的信息，在获取故障信息基础上，通过重新调整控制器的参数或改变控制器的结构来确保系统的性能. 因此，主动容错控制技术是一种更加可靠的容错控制策略.

除此之外，许多现实系统中存在时滞，它也是系统不稳定的重要因素之一. 与无时滞系统的容错控制相比，时滞系统的容错控制研究无疑增加了设计难度[6]，因为时滞系统有其相应的稳定性判据[7, 8, 9, 10]. 目前，虽然关于时滞系统的故障诊断与容错控制问题已经有了一些研究结果，但其仍是一个值得学者们广泛研究的领域. 文[11, 12]针对常时滞系统提出了基于迭代学习观测器故障估计方法. 文[13]针对可能发生的传感器故障，对一类广义时滞切换系统设计了故障估计与补偿方法. 文[14]针对一类具有执行器失效故障的时滞非线性系统，设计了自适应故障补偿方法，目的是寻找自适应故障容错控制器，使系统不仅稳定而且使故障系统能够满足设计性能. 文[15]针对一类离散时间的T-S系统可能发生的执行器故障，主要研究了集成鲁棒故障估计问题，设计了多约束降阶故障估计观测器并利用模糊输出反馈来补偿故障的影响并有效补偿故障使系统稳定.

本文的主要思想是设计主动容错控制率及观测器，使故障系统状态能够跟踪无故障的参考系统状态[16]. 通过建立状态估计误差、 状态跟踪误差、 故障估计误差及输出估计误差的动态方程，并将其整理成广义系统来同时估计时变故障及系统的状态，进而得到能够保证系统跟踪的容错控制率及观测器增益参数.

2 问题的描述

考虑如下的无故障系统参考模型：

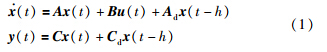
其中，x(t)∈Rn为系统状态向量，u(t)∈Rm为输入向量，y(t)∈Rp为输出向量，其中的n、 m、 p分别为系统状态向量、 输入向量和输出向量的维数； A、 B、 Ad、 C及Cd为适当维数且已知的实常矩阵，状态时滞h∈R+为一个常数，并满足0<h≤hmax.

考虑如下故障系统：

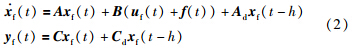
其中，xf(t)∈Rn、 uf(t)∈Rm、 yf(t)∈Rp、 f(t)∈Rm分别为故障系统的状态向量、 容错控制向量、 故障系统输出向量及影响系统行为的故障向量，A、 B、 Ad及C、 Cd则与参考模型相同.

本文的目标是设计容错控制器uf(t)，以确保故障系统的状态收敛到参考系统状态. 控制器设计方案[16]如图 1所示，其中uf(t)=u(t)+uc(t)(t)为故障容错控制向量.

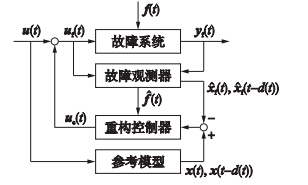图 1 控制策略Fig. 1 The control scheme
图选项

为了使故障系统(2)能够跟踪参考模型(1)，本文考虑如下FTC控制率，如式(3)所示：

其中，K1，K2∈Rm×n，为状态反馈增益矩阵，其作用为确保系统稳定性且在故障时使参考模型x(t)及故障系统xf(t)之间的差值最小化. 除此之外，由于容错控制器的设计还需要知道故障信息，为了估计xf(t)和f(t)，考虑如下PI观测器：

其中，H1∈Rn×p和H2∈Rr×p为观测器的增益矩阵.

3 容错控制率设计

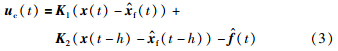
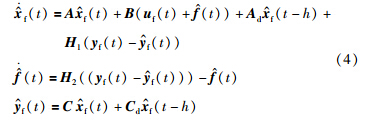
为了方便描述，本文后面的描述中在不出现歧义的情况下将省略t ，如x(t)表示为x，x(t-h)表示为x(h).

在设计中，首先定义状态跟踪误差、 状态估计误差、 输入误差、 故障估计误差、 输出估计误差分别为[16]

通过在式(3)中加减K1xf、 K2xf(h)及f项，可以得到：

因此eu可表示为

根据式(4)、 (5)和式(6)， ep和 es的导数为

故障估计误差的导数为

输出估计误差为

进一步整理可得，输出误差的导数方程为

然后，将式(7)～(9)、 (11)组成如下广义系统：

其中，

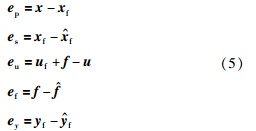
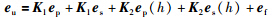
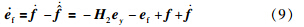
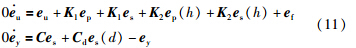
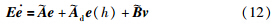
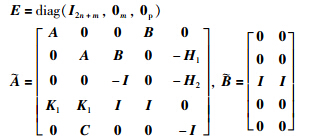
下面给出本文的主要结果：

定理1 已知给定常数γ，若存在适当维数的正定矩阵P1>0、 P2>0、 P3>0，适当维数矩阵Y2、 Y，满足以下不等式：

则状态跟踪误差 ep、 状态估计误差 es及故障估计误差 ef渐近收敛，且从故障及其导数到状态跟踪误差 ep、 状态估计误差 es及故障估计误差 ef的L2增益小于γ. 其中，

其中，sym(A)=A+AT，P1具有如下结构：

其中，Y12、 Y13、 Y14为可逆矩阵，而Y11、 Y15、 Y16、 Y17、 Y18为松弛矩阵. 观测器及控制器的增益矩阵为

证明 选择Lyapunov-Krasovskii函数[8]：

其中，

V(t)的时间导数为

根据Newton-Lebniz公式及广义系统方程(12)，有：

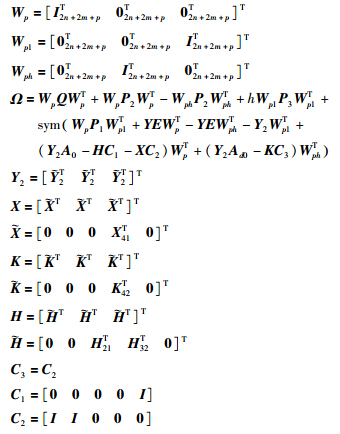
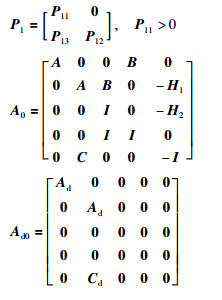
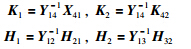
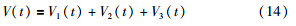
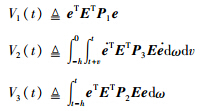
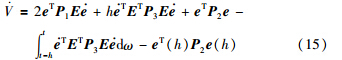
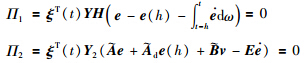
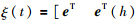
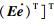其中，Y 、 Y 2为适当维数矩阵[18]且. 在式(15)中加上2Π1和2Π2，有：

考虑到权重L2约束表示为

其中，γ为类扰动项v对误差e的衰减系数，而Q为对称的半正定权矩阵. 若存在lyapunov-krasovskii函数使得：

则广义系统稳定且其范数小于给定界γ.

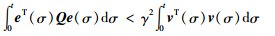
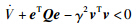
在式(16)中加上 eTQe-γ2vTv项及hξTYP3-1YTξ项，同时减去∫t-htξT(t)YP3-1YTξ(t)dω项，再利用Schur补引理，定理1可证.

4 仿真实例

考虑故障系统[10]：

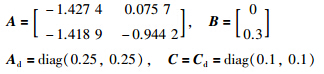
假设状态时滞为h=0.01，系统输入为u(t)=0.5sin t，故障函数选为

当选取参数γ=0.15，Q=diag｛I5，I2｝时，通过求解定理1，可以得到观测器及故障估计增益矩阵：

利用上述参数得到的仿真结果如图 2～5所示. 图 2给出了故障估计的结果.

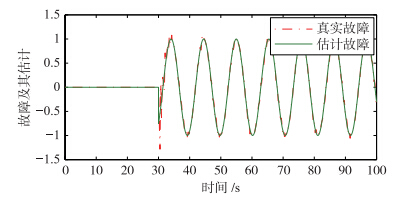图 2 故障及其估计Fig. 2 Faults and their estimation
图选项
图 3 参考模型状态x1、 故障系统状态xf1及观测器状态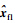比较Fig. 3 Comparison among the reference mode state x1，the faulty system state xf1 and the observer states
图选项
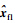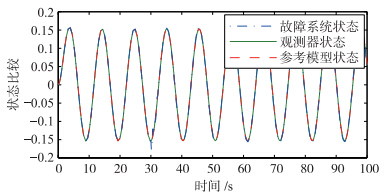图 4 参考模型状态x2、 故障系统状态xf2及观测器状态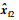比较Fig. 4 Comparison among the reference mode state x2，the faulty system state xf2 and the observer states
图选项
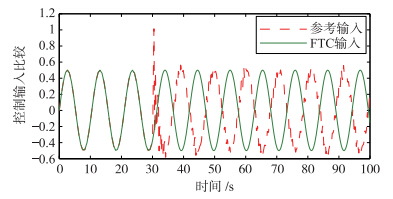图 5 参考输入u(t)与容错控制输入uf(t)Fig. 5 Nominal input u(t) and FTC uf(t)
图选项

从故障估计的结果可以看出，30 s发生故障后，系统很好地检测到故障，并有效地进行了估计.

图 3、 4给出了参考模型状态、 故障模型状态及观测器状态的比较结果.从仿真结果看，在发生故障时刻，系统状态发生了跳变，但由于FTC的作用，2个状态很快实现了对参考模型状态的跟踪.

图 5给出了参考模型输入及故障模型FTC比较结果.

从图 5可以看出，故障前，FTC与参考输入无差别，而当故障发生后，系统很快检测到故障，FTC对故障进行了有效补偿，使得整个系统能够有效跟踪参考模型.

为了验证故障容错控制器在故障时的跟踪性能，本文将其与文[20]附录中给出的经典控制器设计方法进行了比较. 在经典控制器设计中，稳定性的证明及稳定条件的求解均类似于定理1. 仿真实例则与本部分给定的例子相同，求解反馈增益矩阵后，得到的仿真结果如图 6、 7所示.

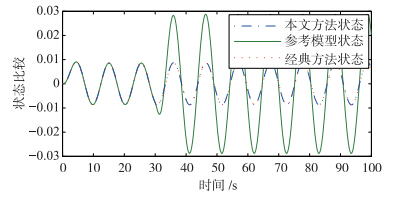图 6 参考模型状态x1、 经典控制方法系统状态xc1

及本文方法系统状态xf1比较Fig. 6 Comparison among the reference mode state x1， the faulty system state xc1 with classic control law and the proposed faulty system state xf1 with control law
图选项
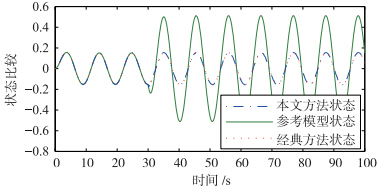图 7 参考模型状态x2、 经典控制方法系统状态xc2 及本文方法系统状态xf2比较Fig. 7 Comparison among the reference mode state x2， the faulty system state xc2 with classic control law and the proposed faulty system state xf2 with control law
图选项

从仿真结果看，当系统无故障(时间小于30 s)时，两种控制方法都能够很好地跟踪参考模型. 但当发生故障后，本文提出的方法跟踪性能要明显优于经典控制方法.

5 结论

本文针对线性时滞系统可能发生的时变故障，设计并利用FTC控制率及观测器增益确保了故障系统状态能够有效跟踪参考模型状态. 将系统状态误差、 跟踪误差、 故障估计误差以及输出误差组成了广义系统，在广义系统稳定性证明中使用了Lyapunov-Krasovskii定理，并将稳定性问题转化为LMI的求解问题，得到了使系统稳定的增益矩阵. 最后，在与经典方法的比较仿真中证明了所提方法的有效性.

参考文献
[1] Tao G, Chen S, Joshi S M. An adaptive actuator failure compensation controller using output feedback[J]. IEEE Transactions on Automatic Control, 2002, 47(3): 506-511.
[2] 姚利娜, 薛霄, 姜斌. 序列连续系统的容错控制[J]. 信息与控制, 2013, 42(1): 13-17. Yao L N, Xue X, Jiang B. Fault tolerant control for a sequential continuous system[J]. Information and Control, 2013, 42(1): 13-17.
[3] Blanke M, Staroswiecki M, Wu N E. Concepts and methods in fault-tolerant control[C]//Proceedings of the 2001 American Control Conference. Piscataway, NJ, USA: IEEE, 2001: 2606-2620.
[4] Zhang Y, Jiang J. Bibliographical review on reconfigurable fault-tolerant control systems[J]. Annual Reviews in Control, 2008, 32(2): 229-252.
[5] Staroswiecki M. On fault handling in control systems[J]. International Journal of Control Automation and Systems, 2008, 6(3): 296-305.
[6] 张柯. 基于观测器的动态系统故障估计和调节[D]. 南京: 南京航空航天大学, 2012. Zhang K. Observer-based fault estimation and accommodation for dynamic systems[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012.
[7] Zhao Y, Wu J, Shi P. H∞control of non-linear dynamic system: A new fuzzy delay partitioning approach[J]. IET Control Theory & Applications, 2009, 3(7): 917-928.
[8] Lin C, Wang Q G, Lee T H, et al. Observer-based control for T-S fuzzy systems with time delay: Delay-dependent design method[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2007, 37(4): 1030-1038.
[9] Fridman E, Shaked U. Delay-dependent H∞control of uncertain delay system[J]. European Journal of Control, 2005, 11(1): 29-37.
[10] Xu S, Lam J, Zhang B, et al. A new result on the delay-dependent stability of discrete systems with time-varying delays[J]. International Journal of Robust and Nonlinear Control, 2014, 24(16): 2512-2521.
[11] Chen W, Saif M. An iterative learning observer for fault detection and accommodation in nonlinear time-delay systems[J]. International Journal of Robust and Nonlinear Control, 2006, 16(1): 1-19.
[12] Chen W, Saif M. Fault detection and accommodation in nonlinear time-delay systems[C]//Proceedings of the 2003 American Control Conference. Piscataway, NJ, USA: IEEE, 2003: 4255-4260.
[13] Jiang B, Staroswiecki M, Cocquempot V. H∞fault detection filter design for linear discrete-time systems with multiple time delays[J]. International Journal of Systems Science, 2003, 34(5): 365-373.
[14] Ye D, Yang G. Adaptive actuator fault compensation for nonlinear time-delay systems[C]//The Sixth World Congress on Intelligent Control and Automation. Piscataway, NJ, USA: IEEE, 2006: 285-289.
[15] Jiang B, Zhang K, Shi P. Integrated fault estimation and accommodation design for discrete-time Takagi-Sugeno fuzzy systems with actuator faults[J]. IEEE Transactions on Fuzzy Systems, 2011, 19(2): 291-304.
[16] Bouarar T, Marx B, Maquin D, et al. Fault-tolerant control design for uncertain Takagi-Sugeno systems by trajectory tracking: A descriptor approach[J]. IET Control Theory & Applications, 2013, 7(14): 1793-1805.
[17] Zhang G J, Han C S, Wu L G, et al. Admissibility and performance analysis of T-S fuzzy descriptor systems with time-delay[C]//IEEE Proceeding of Intelligent Control and Information Processing. Piscataway, NJ, USA: IEEE, 2011: 77-81.
[18] Hamdi H, Rodrigues M, Mechmeche C. State estimation for polytopic LPV descriptor systems: Application to fault diagnosis[C]//7th IFAC Symposium on Fault Detection, Supervision and Safety of Technical Processes Barcelone: Spain, 2009.
[19] Zhang K, Jiang B, Concquempot V. Fast fault estimation and accommodation for dynamical systems[J]. Asian Journal of Control, 2009, 11(6): 643-652.
[20] Bouarar T, Marx B, Maquin D, et al. Trajectory tracking fault tolerant controller design for Takagi-Sugeno systems subject to actuator faults[C]//International Conference on Communications, Computing and Control Applications. Piscataway, NJ, USA: IEEE, 2011: 1-6."
"http://dx.doi.org/10.13976/j.cnki.xk.2015.0469"
中国科学院主管，中国科学院沈阳自动化研究所、中国自动化学会共同主办。
0

文章信息

赵石磊, 郭红, 刘宇鹏
ZHAO Shilei, GUO Hong, LIU Yupeng
基于轨迹跟踪的线性时滞系统容错控制
Fault Tolerant Control for Linear Time-delay System Based on Trajectory Tracking
信息与控制, 2015, 44(4): 469-473.
INFORMATION AND CONTROL, 2015, 44(4): 469-473.
http://dx.doi.org/10.13976/j.cnki.xk.2015.0469

文章历史

收稿日期：2014-06-26
录用日期：2014-09-09
修回日期：2015-02-23

工作空间