1 引言
风电场一般都建在环境比较恶劣的地区,风力机在这种条件下运行时,经常会出现传感器、 执行器故障问题,造成系统不稳定[1, 2],如桨距角传感器故障引起的发电机速度波动问题. 容错控制(fault tolerant control,FTC)能够在系统部件(传感器和执行器)发生故障时,保证风力机满足工作范围内的性能指标,使系统稳定运行.
风力机系统中,由于风速是不断变化的,导致系统的稳态工作点随风速变化,使得风力机系统呈现强非线性特性[3]. 传统的针对单一线性化模型的控制并不能满足系统性能的要求,而线性变参数(linear parameter varying,LPV)增益调度技术通过调度变量,调度每个工作点的线性化模型,使得系统模型更加精确,控制设计更加准确[4]. 再者,LPV增益调度技术允许对复杂非线性系统进行线性化设计,它通过离线计算顶点控制器增益,根据实时可测或估计的调度变量改变控制器增益[5, 6]. 为了追求高的风能利用系数和不断优化输出功率曲线,变桨距控制已成为学者们研究的热点[7, 8]. 然而,桨距系统中经常会出现执行器或传感器故障问题,导致风能利用系数降低、 发电机速度和输出功率波动等一系列问题. 针对桨距系统故障问题合理的容错控制策略是解决此类问题的关键,而LPV技术在容错控制中的应用正引起人们的关注[9, 10]. 文[11]选取风速和执行器故障因子作为调度变量,设计了主动LPV容错控制器,该方法以降低系统性能为代价,解决了执行器故障导致的结构不平衡问题. 文[12]建立了桨距系统的LPV模型,选取桨距角传感器故障因子作为调度参数,采用自适应观测器方法,处理桨距角传感器卡死故障,但所建立的LPV模型比较简单,仅能处理单一故障. 文[13, 14]针对桨距系统中液压油含量过高问题,提出了LPV主动容错控制方法,解决了输出功率发散的问题. 而文[15, 16]给出了一种新的容错控制方法,通过在控制环中嵌入虚拟执行器,重构控制器输入和输出,隐藏执行器故障,保证了系统在执行器发生故障时仍然具有良好的跟踪性能.
本文针对桨距角传感器故障问题,采用完整的风力机LPV模型,提出了基于虚拟传感器的容错控制方法. 将桨距角传感器故障作为调度变量,设计结构类似于Luenberger观测器的虚拟传感器[17, 18]. 图 1为基于虚拟传感器的容错控制系统,主要包括: 风力机、 LPV虚拟传感器、 LPV虚拟观测器和LPV控制器. 当桨距角传感器无故障时,LPV虚拟传感器不起作用,风力机系统在LPV状态反馈控制器的作用下稳定运行. 当桨距角传感器发生故障时,通过引入虚拟传感器来重构控制环,这样通过虚拟传感器产生的输出和无故障时桨距角传感器测量输出一致,消除了桨距角传感器故障导致的发电机速度波动问题. 同时针对传感器故障时,部分状态不能测量的问题,设计一个状态观测器估计所有的状态. 然后由LPV控制器进行状态控制,使系统跟踪参考输入,解决发电机速度波动问题保证恒功率输出. 和文[13, 14]相比,本文具有如下优点: 基于虚拟传感器的容错控制方法在最小限度改变系统结构的前提下,嵌入到原有的风力机控制系统中,任何满足特定要求的控制器都不需要更换; 再者,根据控制器与观测器的分离原则,虚拟传感器可以独立于控制环设计. 文中LPV虚拟传感器、 LPV观测器和LPV控制器的设计采用凸多面体技术和LMI(linear matrix inequality)区域极点配置技术. 最后,针对桨距角传感器经常出现的失效和偏差故障进行仿真,仿真结果表明,基于虚拟传感器的容错控制方法,可以解决桨距角传感器故障引起的发电机速度波动问题,降低风轮气动力矩抖动,减少机械应力,使风力机输出功率恒定.
 |
| 图 1 LPV虚拟传感器容错控制系统Fig. 1 Fault tolerant system using the LPV virtual sensor |
风力机模型主要包括空气动力学子模型,传动机构子模型,功率系统子模型和桨距系统子模型.
2.1 空气动力学子模型空气动力学子模型中,风速通过叶片转化为作用于转子桨叶的力矩Ta(t),使风轮转子以速度ωr(t)旋转. 所捕获的风能依赖于风速vr(t),空气密度ρ,桨叶的等效面积A和转化效率Cp(λ(t),β(t)). 其中,Cp(λ(t),β(t))是桨距角β(t)和叶尖速比λ(t)的函数,气动力矩Ta(t)可由式(1)表示[19]:
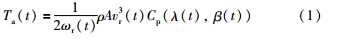
传动机构由低速轴和高速轴组成. 低速轴和高速轴的转动惯量分别为Jr和Jg,摩擦系数分别为Br和Bg. 高低速轴通过齿轮箱连接,两侧的齿轮比为Ng. 考虑传动机构扭力衰减系数Bdt、 扭转刚度Kdt、 传动系统的输出扭矩角θΔ(t)、 电机产生的力矩Tg(t)和发电机转速ωg(t),传动系统的模型如下[19]:
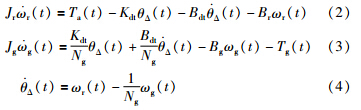
发电机产生的电能通过变流器输送到通用电网中. 发电机的力矩Tg(t)通过跟踪参考力矩Tg,ref(t)获得,变流器可以近似为一个具有时间常数τg的一阶动态系统. 所产生的电能Pg(t)由转换效率ηg决定,有[19]:
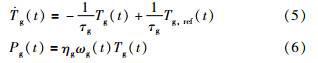
风力机的液压桨距系统由3个独立的桨距执行器组成,可以把它看作一个二阶动态系统. 桨距执行器模型[20]:
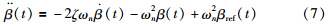
空气动力学子模型中的Cp(λ(t),β(t))是风力机呈现非线性特性的主要因素. 利用泰勒公式将气动转矩Ta(t)在点(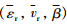 )展开有:
)展开有:
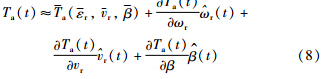
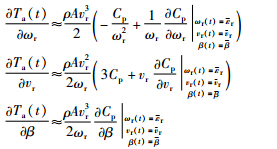
转子速度ωr(t)和桨距角β(t)依赖于风速vr(t),因此,展开后的泰勒表达式的分量均可近似为风速vr(t)的线性函数,意味着可以将风速作为LPV模型的增益调度变量: θv(t)∶=vr(t). 选取系统状态变量x(t)=(β(t),β·(t),θΔ(t),ωg(t),ωr(t),Tg(t))T,控制变量u1(t)=(βref,Tg,ref),扰动w(t),记u(t)=(u1(t),w(t))T. 并选取桨距角和发电机速度作为观测输出y(t)=(βref,ωg)T. 考虑桨距角传感器故障时将影响观测输出,相当于输出矩阵改变. 因此,选取故障因子f(t)作为另一增益调度变量: θf(t)∶=f(t). 结合式(1)~式(8)得包括传感器故障的风力机LPV模型:
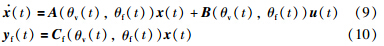
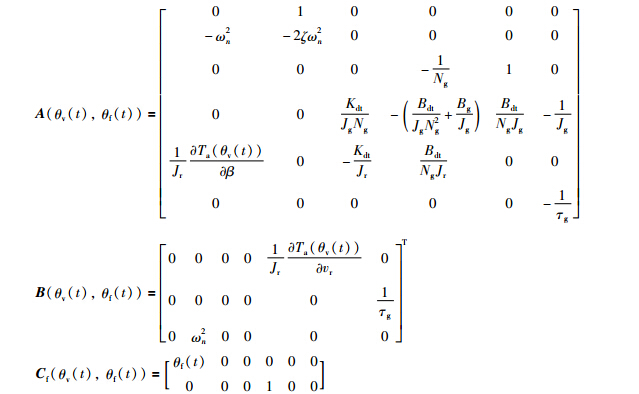
针对桨距角传感器故障问题,利用虚拟传感器重构故障传感器输出,设计LPV控制器,解决桨距角故障导致的发电机速度波动问题.
3.1 LPV虚拟传感器LPV虚拟传感器的静态和动态结构形式由下面的行秩条件决定:
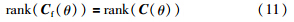

(2) 若不满足式(11)的行秩条件,说明桨距角传感器完全失效,则无法直接重构桨距角传感器输出. 因此,通过引入虚拟传感器动态部分重构桨距角传感器输出,引入矩阵C*(θ)P(θ)Cf(θ). 重构输出为动态形式:
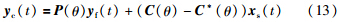
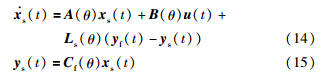
风力机系统通过跟踪参考输入r(t)进行状态反馈控制. 在传统的状态控制律u(t)=K(θ)x(t)的基础上,加入输入参考控制增益Nx(θ),将非状态参考输入转化成状态参考输入,同时通过加入前馈控制增益Nuθ)消除稳态误差. 因此,LPV控制器的具体形式为

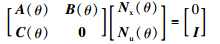
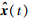 在传感器出现故障时不能完全得到,利用估计状态(t)代替实际状态. 因此,设计了如下形式的LPV状态观测器:
在传感器出现故障时不能完全得到,利用估计状态(t)代替实际状态. 因此,设计了如下形式的LPV状态观测器:
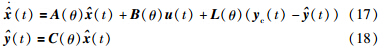
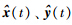 分别是估计状态和估计输出,L(θ)是状态观测器的增益.
分别是估计状态和估计输出,L(θ)是状态观测器的增益. 最后,虚拟传感器容错控制方案如图 2所示.
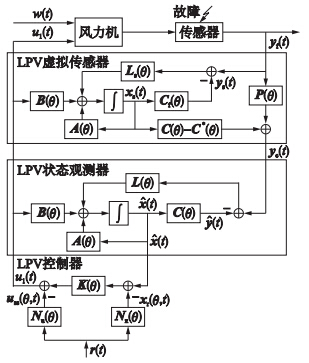 |
| 图 2 LPV虚拟传感器FTC方案Fig. 2 The FTC scheme for LPV virtual sensor |
在基于观测器的状态反馈控制系统中,整个闭环系统的极点由状态反馈控制系统的极点和观测器极点构成,观测器和控制器可以分开设计这就是分离原则[22]. 本文把
分离原则应用到基于虚拟传感器的LPV容错控制系统,通过简单的分析可得,基于虚拟传感器的容错控制系统也存在类似的分离原理,即所设计的LPV虚拟传感器、 LPV观测器和LPV控制器可以独立设计.
引入观测器误差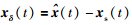 和虚拟传感器误差xΔ(t)=xs(t)-x(t)分别来衡量观测器的观测能力和虚拟传感器重构故障的能力,则:
和虚拟传感器误差xΔ(t)=xs(t)-x(t)分别来衡量观测器的观测能力和虚拟传感器重构故障的能力,则:



假设uss(θ,t)=0,xr(θ,t)=0,考虑系统状态x(t)不能完全得到. 将控制律式(16)变为
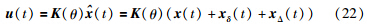
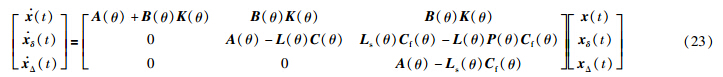
由式(23)得:
(1) 矩阵K(θ)仅通过复合矩阵A(θ)+B(θ)K(θ)影响过程状态x(t)的性能.
(2) 矩阵L(θ)通过复合矩阵A(θ)-L(θ)C(θ)影响观测器误差xδ(t)的性能.
(3) 矩阵Ls(θ)通过复合矩阵A(θ)-Ls(θ)Cf(θ)影响虚拟传感器误差xΔ(t)的性能.
因此,闭环系统的特征值集合可表示为
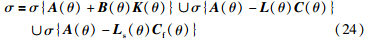
通过以上分析可以看出,由于式(21)中的系数矩阵依赖于调度变量θ,因此在分别对所设计的LPV虚拟传感器、 LPV观测器和LPV控制器求解时,需要求解无限个约束条件使问题复杂化. 文[23]中给出了解决这个问题的一个有效的方法,即把依赖于调度变量的矩阵转化成在凸多面体Λ中随调度变量变化的矩阵,然后,求解凸多面体顶点处的LPV虚拟传感器、 LPV观测器和LPV控制器. 最后通过调度变量调度每个顶点处的控制器. 这里选(θf,min,θv,min)、 (θf,min,θv,max)、 (θf,max,θv,min)、 (θf,max,θv,max)4个顶点,转化可以表示为
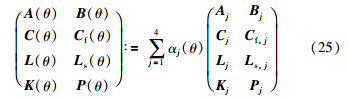
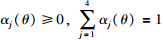 ,根据式(16)和式(25),将式(21)转化为
,根据式(16)和式(25),将式(21)转化为


定义(LMI区域): 设D为复平面的一个子集,如果存在对称矩阵Φ=[Φk,l]∈Rm×m和矩阵Ψ=[φk,l]∈Rm×m,且D={z∈H∶fD(z)<0},其中[24]:
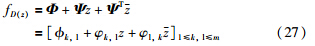
选择复平面左半开区域H中的垂直条形区域Dv={s∈H∶Smin<Re(s)<Smax}与半径为R,中心在(-q,0)的圆盘Dc(γ,q)相交部分为LMI区域. 由定义知,使式(26)的极点位于LMI区域,必须保证下列不等式成立[24]:
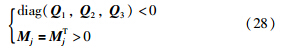
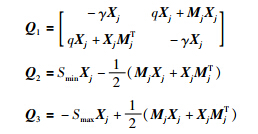
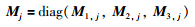
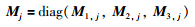

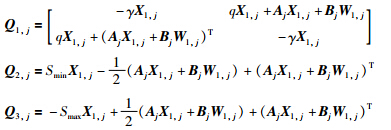
设计步骤:
第1步: 选择调度参数: θv(t)∈[18 m/s,25 m/s],θf(t)∈[0,1],建立风力机LPV模型.
第2步: 判断式(11)行秩条件,求解矩阵P(θ)、 C*(θ).
第3步: 选择LMI区域,求解式(29),获LPV控制器增益K(θ),LPV观测器增益L(θ),LPV虚拟传感器增益Ls(θ)为
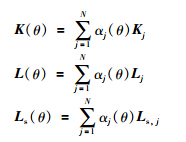
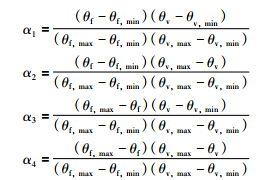
结论: 基于虚拟传感器的容错控制能够处理桨距角传感器故障导致的发电机速度波动问题.
5 仿真研究 5.1 故障设计本文针对桨距角传感器经常出现的失效和偏差故障进行容错控制,研究桨距角传感器出现故障时,对风力机风轮气动力矩、 发电机速度和输出功率的影响. 在仿真时假设故障已经很好地估计出,这里仅简单对故障发生时刻和故障大小进行设计,通过θf来指示系统有无故障以及故障大小.
故障1: 在45~50 s,桨距角传感器完全失效,输出βm=0°,此时相当于θf=0.
故障2: 在60~65 s,桨距角传感器出现偏差,输出βm=κβm1,κ=0.8,此时相当于θf=0.8.
风力机仿真参数见表 1.
| 参数 | 值 | 参数 | 值 |
| Kdt | 2.7×109 N·m/rad | Bdt | 945 N·m/(rad/s) |
| A | 10 387 m2 | Bg | 3.03 N·m/(rad/s) |
| ρ | 1.225 kg/m3 | Br | 27.8 N·m/(rad/s) |
| Jr | 55×106 kg·m2 | θv,min | 18 m/s |
| Jg | 390 kg·m2 | θv,max | 25 m/s |
| θf,min | 0 | θf,max | 1 |
| Ng | 95 |
选择合适的LMI区域,保证虚拟传感器容错控制方法能够快速处理桨距角传感器故障导致的发电机速度波动问题,确保系统稳定.
在风力机Benchmark模型中对虚拟传感器容错控制方法进行仿真,仿真时间为80 s,风力机运行在恒功率输出的状态下,仿真结果如图 3~8所示. 图 3给出了桨距角传感器无故障时的虚拟传感器重构输出,可以看出虚拟传感器完全可以跟踪实际桨距角传感器输出,并且消除了噪声对实际传感器的影响. 对于桨距角传感器的失效和输出偏差故障,由图 4和图 5说明. 在45~50 s中桨距角传感器测量丢失,其输出βm=0°,同样在60~65 s中桨距角传感
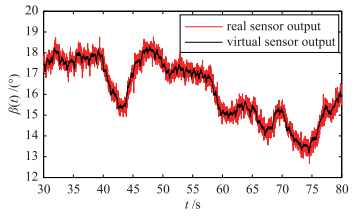 |
| 图 3 桨距角参考值和虚拟传感器输出值Fig. 3 The value of pitch reference and the virtual sensor output |
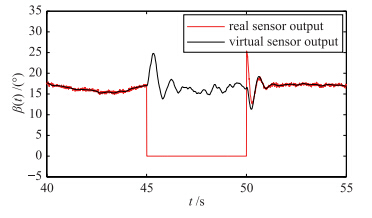 |
| 图 4 桨距传感器完全失效Fig. 4 Pitch sensor complete failure |
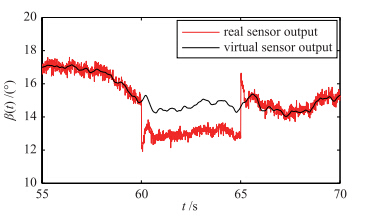 |
| 图 5 桨距传感器偏差输出Fig. 5 The deviation of pitch sensor output |
 |
| 图 6 发电机速度Fig. 6 Generator speed |
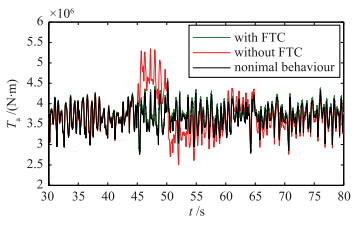 |
| 图 7 风力机气动力矩Fig. 7 Torque of a wind turbine rotor |
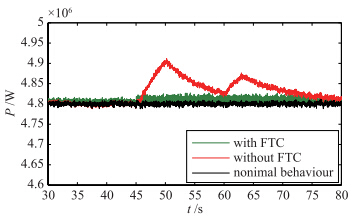 |
| 图 8 发电机功率Fig. 8 Generator power |
器输出为实际输出的0.8倍,而虚拟传感器的输出和无故 障时几乎一样. 这样用虚拟传感器的输出来代替实际传感器的输出,使风力机在桨距角传感器故障时接近无故障系统,保证系统特性不因故障的存在而改变. 图 6是系统运行时的发电机速度,在系统出现上述两种故障时,发电机速度发生波动,导致系统震荡,从图中亦可以看出: 在故障发生和结束的瞬间,发电机速度波动比较大,在故障消失后发电机速度要经过相当长的时间才可以获得无故障时的特性. 图 7和图 8进一步说明了风力机桨距角故障对系统造成的影响. 图 7为气动力矩,在实际系统中很难测到,这里通过仿真说明桨距角对风力机转速影响的原因. 图中显示在桨距角出现故障时造成气动力矩变化,造成风力机转速波动,并且引起塔架抖动,降低风力机的机械性能. 发电机速度波动,进一步引起了发电机输出功率变化. 并且从图 8中可以看出,对功率的影响比较大,过大的功率接入电网将引起电网波动,严重时可能造成电网瘫痪. 而在基于虚拟传感器的容错控制方法下,桨距角传感器的故障被消除,保证了发电机速度和输出功率的平滑性.
6 总结本文根据LPV控制理论,选取风速和桨距角传感器故障作为调度变量,建立了风力机LPV模型. 通过判断输出矩阵的行秩条件给出了虚拟传感器结构. 然后,根据分离原则,利用LMI区域极点配置技术,得到LPV虚拟传感器、 LPV虚拟观测器和LPV控制器. 最后,把基于虚拟传感器的容错控制方法应用到风力机Benchmark模型中,仿真结果表明: 所设计的基于虚拟传感器的LPV容错控制器,能够处理桨距角传感器失效和偏差故障,解决桨距角传感器故障导致的发电机速度波动问题.
| [1] | Munteanu I, Bratcu A I, Cutululis N A, et al. Optimal control of wind energy systems: Towards a global approach[M]. Berlin, Germany: Springer, 2008. |
| [2] | 沈艳霞, 贺庆楠, 潘庭龙, 等. 风能转换系统T-S模糊鲁棒容错控制[J]. 信息与控制, 2013, 42(6): 750-757, 764. Shen Y X, He Q N, Pan T L, et al. T-S fuzzy robust fault-tolerant control strategy for wind energy conversion system[J]. Information and Control, 2013, 42(6): 750-757, 764. |
| [3] | Badihi H, Zhang Y, Hong H. Model reference adaptive fault-tolerant control for a wind turbine against actuator faults[C]//2013 Conference on Control and Fault-Tolerant Systems (SysTol). Piscataway, NJ, USA: IEEE, 2013: 498-503. |
| [4] | Bianchi F D, Battiata H, Mantz R J. Wind turbine control systems principles modelling and gain scheduling design[M]. Berlin, Germany: Springer, 2006. |
| [5] | Shamma J S, Athans M. Analysis of gain scheduled control for nonlinear plants[J]. IEEE Transactions on Automatic Control, 1990, 35(8): 898-907. |
| [6] | 沈艳霞, 朱芸, 纪志成. LPV动态补偿的风能转换系统变桨距控制[J]. 控制理论与应用, 2009, 26(11): 1282-1288. Shen Y X, Zhu Y, Ji Z C. Variable pitch control for wind energy conversion system with LPV dynamic compensation[J]. Control Theory and Applications, 2009, 26(11): 1282-1288. |
| [7] | 崔双喜, 王维庆, 周顺平. 基于半实物仿真的风力机变桨距控制实验[J]. 实验室研究与探索, 2014, 33(7): 4-7, 12. Cui S X, Wang W Q, Zhou S P. Variable pitch controlled experimental research based on wind turbine semi-physical simulation[J]. Research and Exploration in Laboratory, 2014, 33(7): 4-7, 12. |
| [8] | 郭百顺, 秦斌, 邵军, 等. 风电机组独立变桨距控制策略研究[J]. 湖南工业大学学报, 2014, 28(2): 42-45. Guo B S, Qin B, Shao J, et al. Research on the control strategy of independent variable pitch of wind turbine[J]. Journal of Hunan University of Technology, 2014, 28(2): 42-45. |
| [9] | Bianchi F D, Mantz R J, Christansen C F. Gain scheduling control of variable-speed wind energy conversion systems using quasi-LPV models[J]. Control Engineering Practice, 2005, 13(2): 247-255. |
| [10] | Hallouzi R, Verdult V, Babuska R, et al. Fault detection and identification of actuator faults using linear parameter varying models[C]//16th IFAC Triennial World Congress. Kidlington, UK: IFAC, 2005: 119-124. |
| [11] | Sloth C, Esbensen T, Stoustrup J. Active and passive fault-tolerant LPV control of wind turbines[C]//IEEE American Control Conference (ACC). Piscataway, NJ, USA: IEEE, 2010: 4640-4646. |
| [12] | Chen L, Shi F, Patton R. Active FTC for hydraulic pitch system for an off-shore wind turbine[C]//IEEE Conference on Control and Fault-Tolerant Systems (SysTol). Piscataway, NJ, USA: IEEE, 2013: 510-515. |
| [13] | 吴定会, 李意扬, 纪志成. 风力机的线性变参数主动容错控制[J]. 控制理论与应用, 2014, 31(4): 425-430. Wu D H, Li Y Y, Ji Z C. Active fault-tolerant linear-parameter varying control of wind turbines[J]. Control Theory & Applications. 2014, 31(4): 425-430. |
| [14] | 吴定会, 李意扬, 纪志成. 风能转换系统的LPV主动容错控制[J]. 控制工程, 2014, 21(5): 712-717. Wu D H, Li Y Y, Ji Z C. Active fault tolerant LPV control of wind energy conversion system[J]. Control Engineering, 2014, 21(5): 712-717. |
| [15] | Osella E, Haimovich H, Seron M M. Fault-tolerant control under controller-driven sampling using a virtual actuator strategy[C]//2013 3rd Australian Control Conference (AUCC). Piscataway, NJ, USA: IEEE, 2013: 289-294. |
| [16] | Rotondo D, Puig V, Nejjari F, et al. A fault-hiding approach for the switching quasi-LPV fault tolerant control of a four-wheeled omnidirectional mobile robot[J]. IEEE Transactions on Industrial Electronics, 2014, 99(1): 1-11. |
| [17] | Blanke M, Schrode J. Diagnosis and fault-tolerant control[M]. Berlin, Germany: Springer, 2006. |
| [18] | Nazari R, Seron M M, Yetendje A. Invariant-set-based fault tolerant control using virtual sensors[J]. IET Control Theory & Applications, 2011, 5(9): 1092-1103. |
| [19] | Esbensen T, Sloth C. Fault diagnosis and fault-tolerant control of wind turbines[M]. Aalborg Danmark: Aalborg University, 2009. |
| [20] | Bakka T, Karimi H R, Christiansen S. Linear parameter-varying modeling and control of an offshore wind turbine with constrained information[J]. IET Control Theory & Applications, 2014, 8(1): 22-29. |
| [21] | Franklin G F, Workman M L, Powell D. Digital control of dynamic systems[M]. 3th ed. London, UK: Prentice Hall, 1997. |
| [22] | 吴爱国, 段广仁. 广义线性系统基于PI观测器鲁棒极点配置分离原理[J]. 应用数学, 2007(4): 771-776. Wu A G, Duan G R. Separation principle for robust pole assignment based on PI observers in descriptor linear systems[J]. Mathematica Applicata, 2007(4): 771-776. |
| [23] | Rodrigues M, Theilliol D, Aberkane S, et al. Fault tolerant control design for polytopic LPV systems[J]. International Journal of Applied Mathematics and Computer Science, 2007, 17(1): 27-37. |
| [24] | Chilali M, Gahinet P. H∞design with pole placement constraints: An LMI approach[J]. IEEE Transactions on Automatic Control, 1996, 41(3): 358-367." |



