` 1 引言
偏最小二乘(partial least squares,PLS)算法可以有效地解决变量之间的多重相关性问题,而且适用于小样本容量建模,是工程技术等领域中常用的一种建模方法[1, 2]. 标准PLS适用于解决线性问题,而对于非线性问题的处理效果并不理想. 近些年来,核函数方法广泛应用于机器学习领域并取得了迅速发展,出现了许多基于核函数的机器学习方法,例如支持向量机(SVM)、 核主元分析(KPCA)、 高斯过程(GP)等[3, 4, 5, 6, 7, 8, 9]. 为解决标准PLS算法不适于处理非线性过程的问题,Rosipal等[10]将核函数方法应用到PLS中,提出了核偏最小二乘(kernel partial least squares,KPLS)算法,成功地将PLS推广到非线性过程. KPLS方法通常是采用单一核函数结合一种修改的PLS算法实现非线性建模. 由于单一核函数往往难以完整地描述数据的分布特征,Smits等[11]提出混合核函数方法以提高支持向量机的性能. 王华忠等[12]提出混合核偏最小二乘(mixed kernel partial least squares,MKPLS)算法,利用混合核函数代替KPLS中的单一核函数,其数据适应能力与KPLS相比有所提高.
局部加权学习(local weighted learning,LWL)[13]算法通过一种距离函数确定各训练样本的权值,从而在待测样本点附近构造局部模型,适于在线快速学习,泛化能力强. 而且其加权学习的特点恰好能够在一定程度上解决最小二乘(least squares,LS)类算法对异常数据敏感的问题[14].
本文将LWL引入MKPLS建模,提出了一种局部加权混合核偏最小二乘(local weighted mixed kernel partial least squares,LWMKPLS)算法. 该算法针对每个待测样本数据通过局部加权算法有区别地运用各个训练样本,并采用MKPLS建模方法建立在线局部模型. 运用该方法进行数值仿真并采用来自工业双酚A生产装置的现场数据进行软测量建模仿真,取得了良好的仿真效果.
2 核函数及混合核函数方法的原理核函数方法的基本思想是通过隐式非线性函数将原始数据映射到高维特征空间,进而可以在高维特征空间中运用线性算法[12, 15]. 将映射通过隐式非线性函数φ定义:

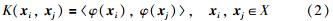
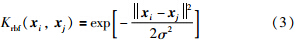
典型的全局核函数如多项式核函数为
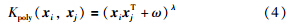
在核函数方法中,核函数的类型和参数的选择非常重要. 例如,径向基核函数适用于提取样本的局部性质,局部学习能力强而泛化能力弱; 多项式核函数则适用于提取样本的全局性质,泛化能力强而局部学习能力弱[16]. 因此单一核函数难以完整地描述数据的分布特征. 为提高核函数对数据的适应能力,可以采用混合核函数方法[16, 17, 18]. 常用的一种混合核函数是将径向基核函数和多项式核函数通过下式相结合:
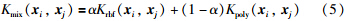
通常建立全局模型时,是对所有训练样本一次性建模,模型建立后便不再变化,因此全局模型对工况变化的适应能力较差、 泛化能力弱[19, 20]. 本文引入LWL算法,模型在对每个待测样本进行输出估计时都要进行模型更新从而建立在线局部模型并估计当前待测样本的输出.
设样本数据集为D={xi,yi}(i=1,2,…,n),其中xi∈Rp为p维自变量,yi∈Rq为q维因变量,则多元线性回归可表示为

根据LWL算法,局部建模时由于各个训练样本与当前待测样本的距离不同,各训练样本在参与建模时的相应权值也不同. 假设第i个样本的权值为wi,对各样本数据直接加权,式(6)变为如下形式:

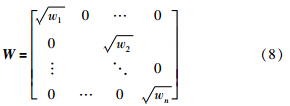
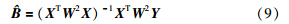
运用基于核函数的偏最小二乘算法对非线性问题进行处理时,算法采用不同的核函数将得到不同的处理效果. 单一核函数对数据分布的适应能力有限,使传统的KPLS算法对于非线性较强过程的处理能力受到约束. 本文提出的局部加权混合核偏最小二乘算法采用混合核函数,并兼具不同核函数的特性,因此对非线性过程数据的适应能力更强. 根据核函数将原始输入映射到高维特征空间,则可在高维特征空间中运用线性算法,并采用线性局部加权学习算法建立在线局部模型,使模型具有较好的泛化能力,从而能更好地适应工况的变化.
设训练样本容量为ntrain,自变量维数为p,因变量维数为q. Xtrain(ntrain×p)为训练样本的自变量数据矩阵,Ytrain(ntrain×q)为训练样本因变量数据矩阵. 设当前待测样本输入为xtest∈Rp,局部加权混合核偏最小二乘算法首先通过混合核函数将原始输入数据映射到高维特征空间. 然后根据高维特征空间中待测样本与各个训练样本的距离计算样本权值,并对高维特征空间中的样本数据加权. 最后运用KPLS回归算法建立局部模型来估计当前待测样本的输出ytest∈Rq.
根据核函数原理和KPLS算法,通过式(5)构造混合核函数Kmix对样本集输入数据Xtrain与xtest进行核变换. 设混合核函数Kmix对应的隐式非线性映射函数φ将训练样本点输入xtrain,i∈Rp(i=1,2,…,ntrain)映射为φtrain,i∈Fs,将xtest映射为φtest∈Fs,Fs为高维特征空间. Xtrain映射到高维特征空间后变为φtrain(ntrain×s),那么通过混合核函数Kmix计算可以得到核矩阵Ktrain(ntrain×ntrain)与核向量Ktest∈Rtrainn
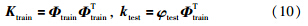
由于KPLS回归算法是将原始数据通过核函数映射到高维特征空间后,采用修改的NIPALS-PLS算法在高维特征空间里对映射后的数据进行线性PLS回归建模,因此可以在高维特征空间中根据映射后的输入数据计算样本权值,然后根据线性局部加权回归思想对映射后的数据进行加权,最后采用KPLS算法建立局部模型.
本文在高维特征空间中采用欧氏距离定义距离函数,则第i个训练样本点与待测样本点在高维特征空间F中的距离为
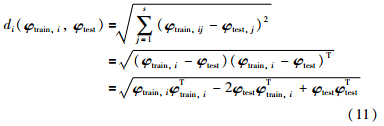
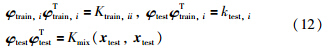
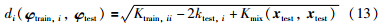
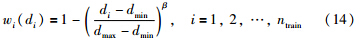
通过式(13)和式(14)计算得到映射到高维特征空间F中的训练样本的权值,根据式(8)构成对角权矩阵W,在高维特征空间里对φtrain和对应输出Ytrain进行加权:
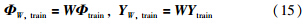
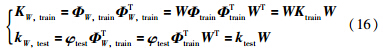
(1) 令i=1,K1=KW,train,Y1=YW,train.
(2) 初始化ui,令ui等于Yi的任何一列.
(3) ti=Kiui/Kiui .
(4) ci=YTiti.
(5) ui=Yici/Yici .
(6) 如果ti收敛,即本次计算所得ti与上次计算所得ti之差小于设定阈值,则转至步骤(7),否则返回至步骤(3).
(7) 令ti+1=ti,ui+1=ui并计算残差:
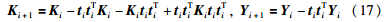
(9) 根据以上步骤得到主成分矩阵T=[t1,t2,…,th],U=[u1,u2,…,uh],回归系数矩阵为
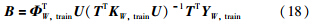
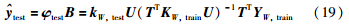
(1)根据式(5)构造混合核函数并将训练样本输入数据Xtrain和待测样本xtest进行混合核变换,通过混合核函数计算得到核矩阵Ktrain与核向量Ktest.
(2)在高维特征空间按式(13)和式(14)计算高维空间中训练样本的权值,构成对角权矩阵W.
(3) 根据式(15)和式(16)对Ktrain、 Ktest和训练样本输出Ytrain加权处理得到KW,train、 kW,test以及YW,train.
(4) KW,train、 kW,test和YW,train经中心化处理,然后通过KPLS算法建立局部回归模型并估计待测样本点的输出. 算法结构如图 1所示.
 |
| 图 1 LWMKPLS算法结构图Fig. 1 The structure of LWMKPLS |
局部加权混合核偏最小二乘算法需要确定的参数包括径向基核函数的核宽度σ,多项式核函数参数ω、 λ,混合系数α等. 通过调节混合系数α可以使混合核函数适应不同的数据分布,相当于在选择核函数时加入了具体非线性过程的先验知识,从而有效地提高模型的非线性处理能力[12].
4 LWMKPLS算法仿真实例 4.1 LWMKPLS算法的数值仿真设非线性系统的输入变量为x1、 x2、 x3、 x4、 x5、 x6,输出变量为y. 输入变量之间存在着一定的相关性,即x4=x1+x2,x5=x2+x3+10,x6=x1+x4. 为了模拟工业过程的工况变化,将系统设置为两段. 系统在第一段中x1,x2,x3∈[-2,0],输入输出间的关系为y=3cos x1+x2·x3+exp(x4/2)+x5-x6+ξ; 系统在第二段中x1,x2,x3∈(0,2],输入输出间的关系为y=4sin x1+x2·x3-exp(x4/2)+x5-x6+ξ. 其中ξ是均值为0,方差为0.1的高斯噪声.
通过上述系统在两段模拟工况中分别产生200组样本数据,并从两段模拟工况中各取160组样本组成样本数为320的训练集用于模型训练,剩余80组样本作为测试集用于模型效果测试. 采用上述LWMKPLS算法建立该系统输出的软测量模型,在运用局部加权算法时权函数参数β取0.5. LWMKPLS软测量模型参数通过网格搜索方法确定为σ=0.866,ω=1,λ=1,α=0.85,主元个数h=18. 为作对比,分别用MKPLS方法和LWKPLS方法建立该系统输出的软测量模型. 其中MKPLS模型参数为σ=0.866,ω=1,λ=1,α=0.5,主元个数h=31; LWKPLS模型采用径向基核函数,参数σ=1,主元个数h=18. 以均方根误差、 平均相对误差和最大相对误差作为模型误差性能指标,将LWMKPLS模型的估计效果与MKPLS模型和LWKPLS模型的估计效果进行比较,测试结果如表 1所示.
| 均方根误差RMSE | 最大相对误差MAXE | 平均相对误差MRE | |
| MKPLS | 0.128 6 | 3.122 4% | 0.920 4% |
| LWKPLS | 0.126 4 | 3.349 1% | 0.867 1% |
| LWMKPLS | 0.119 5 | 3.286 6% | 0.856 8% |
表 1中各项误差性能指标的计算方法如下:
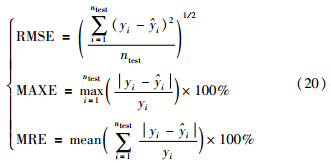
本仿真的数据来自某双酚A(bisphenol A,BPA)生产装置的结晶塔C301以及C301的前级脱水塔C201. 采用本文提出的建模方法对双酚A生产过程中结晶塔C301出口组分中的苯酚含量进行在线软测量建模. 分析生产工艺及流程,确定影响C301出口组分中苯酚含量的主要因素,将结晶塔C301的进料流量、 塔内温度、 塔内液位以及前级脱水塔C201的输出变量即C201出口组分中的苯酚含量、 BPA含量、 杂质24BPA含量,共6个变量作为软测量模型的输入辅助变量,以结晶塔C301出口组分中的苯酚含量作为模型输出主导变量. 从现场取回119组结晶塔C301出口组分苯酚含量的人工分析值和与之对应的辅助变量现场数据作为样本数据集,其中90组用于模型训练,剩余29组用于模型效果测试. 考虑到各变量由于量纲和单位不同会对建模精度产生影响,首先对样本进行标准化处理. 通过样本数据观察分析可知训练样本集中含有一定数量的异常样本点.
采用LWMKPLS算法建立结晶塔出口组分苯酚含量的在线软测量模型,在运用局部加权算法时权函数参数β取2. 通过网格搜索方法确定模型参数为σ=1.414,ω=1,λ=1,α=0.9,提取主元数h=3. 为验证LWMKPLS建模方法的有效性,分别用MKPLS方法和LWKPLS方法建立了结晶塔C301出口组分苯酚含量的软测量模型,将LWMKPLS模型的估计效果与MKPLS模型和LWKPLS模型的估计效果进行比较,测试结果如表 2和图 2所示.
| 均方根误差RMSE | 最大相对误差MAXE | 平均相对误差MRE | |
| MKPLS | 0.719 50 | 2.632 5% | 0.862 54% |
| LWKPLS | 0.875 99 | 3.508 4% | 0.981 81% |
| LWMKPLS | 0.665 71 | 2.182 0% | 0.821 52% |
 |
| 图 2 结晶塔出口组分苯酚含量测试结果图Fig. 2 Phenol content test results of the crystal tower export composition |
根据表 2和图 2,综合比较各项误差性能指标可知,LWMKPLS模型的估计效果最佳,其均方根误差、 最大相对误差和平均相对误差与MKPLS模型和LWKPLS模型相比均有明显减小. 由于实际工业过程通常工况较复杂,而采用LWL算法的LWMKPLS模型泛化能力更强,因此其估计效果优于全局MKPLS模型; 由于LWMKPLS模型采用了混合核函数,提高了模型对过程非线性的适应能力,所以其估计效果与LWKPLS模型相比,模型精度有所提高. 从仿真实验计时测得LWMKPLS模型对单个样本的在线估计用时仅0.023 s,能够满足实际工程应用要求.
5 结语本文提出了一种局部加权混合核偏最小二乘算法. 该算法采用混合核函数方法,与单核函数相比,非线性适应能力更强; 采用局部加权思想,在一定程度上减少了异常样本点对建模精度的影响,建立在线局部模型提高了模型的泛化性能,使模型精度进一步提高. 该算法在数值仿真中的结果以及采用来自工业双酚A生产装置的现场数据进行软测量建模的仿真结果证明了算法的有效性.
| [1] | 王惠文. 偏最小二乘回归方法及其应用[M]. 北京: 国防工业出版社, 1999. Wang H W. Partial least squares regression method and application[M]. Beijing: National Defence Industry Press, 1999. |
| [2] | 吕游, 刘吉臻, 杨婷婷, 等. 基于PLS特征提取和LS-SVM结合的NOx排放特性建模[J]. 仪器仪表学报, 2013, 34(11): 2418-2424. Lü Y, Liu J Z, Yang T T, et al. NOx emission characteristic modeling based on feature extraction using PLS and LS-SVM[J]. Chinese Joumal of Scientific Instrument, 2013, 34(11): 2418-2424. |
| [3] | 顾亚祥, 丁世飞. 支持向量机研究进展[J]. 计算机科学, 2011, 38(2): 14-17. Gu Y X, Ding S F. Advances of support vector machines(SVM)[J]. Computer Science, 2011, 38(2): 14-17. |
| [4] | Liu G H, Zhou D W, Xu H X, et al. Model optimization of SVM for a fermentation soft sensor[J]. Expert Systems with Applications, 2010, 37(4): 2708-2713. |
| [5] | 张淑宁, 王福利, 何大阔, 等. 在线鲁棒最小二乘支持向量机回归建模[J]. 控制理论与应用, 2011, 28(11): 1601-1606. Zhang S N, Wang F L, He D K, et al. Modeling method of online robust least-squares-support-vector regression[J]. Control Theory & Applications, 2011, 28(11): 1601-1606. |
| [6] | 杜卓明, 屠宏, 耿国华. KPCA方法过程研究与应用[J]. 计算机工程与应用, 2010, 46(7): 8-10. Du Z M, Tu H, Geng G H. KPCA method research and application process[J]. Computer Engineering and Applications, 2010, 46(7): 8-10. |
| [7] | 雷萌, 李明. 采用KPCA特征提取的近红外煤炭发热量预测模型[J]. 化工学报, 2012, 63(12): 3991-3995. Lei M, Li M. NIRS prediction model of calorific value of coal with KPCA feature extract[J]. Journal of Chemical Industry and Engineering (China), 2012, 63(12): 3991-3995. |
| [8] | Ni W D, Tan S K, Ng W J, et al. Moving-window GPR for nonlinear dynamic system modeling with dual updating and dual preprocessing[J]. Industrial and Engineering Chemistry Research, 2012, 51(18): 6416-6428. |
| [9] | 何志昆, 刘光斌, 赵曦晶, 等. 高斯过程回归方法综述[J]. 控制与决策, 2013, 28(8): 1121-1129, 1137. He Z K, Liu G B, Zhao X J, et al. Overview of Gaussian process regression[J]. Control and Decision, 2013, 28(8): 1121-1129, 1137. |
| [10] | Rosipal R, Trejo L J. Kernel partial least squares regression in reproducing kernel hilbert space[J]. Journal of Machine Learning Research, 2001, 2(2): 97-123. |
| [11] | Smits G F, Jordaan E M. Improved SVM regression using mixtures of kernels[C]//Proceedings of the 2002 International Joint Conference on Neural Networks. Piscataway, NJ, USA: IEEE, 2002: 2785-2790. |
| [12] | 王华忠, 俞金寿. 混合核函数PLS建模方法及在软测量中的应用[J]. 计算机与应用化学, 2007, 24(2): 239-242. Wang H Z, Yu J S. Studies on modeling using mixtures of kernels partial least squares and its application to soft sensing[J]. Computers and Applied Chemistry, 2007, 24(2): 239-242. |
| [13] | Atkeson C G, Moore A W, Schaal S. Locally weighted learning[J]. Artificial Intelligence Review, 1997, 11(1/2/3/4/5): 11-73. |
| [14] | 杨慧中, 陈定三. 局部惩罚加权核偏最小二乘算法及其应用[J]. 控制工程, 2011, 18(6): 886-889. Yang H Z, Chen D S. Local penalized weighted kernel partial least squares algorithm and its applications[J]. Control Engineering of China, 2011, 18(6): 886-889. |
| [15] | 刘晓飞. 基于核函数优化的KPCA方法及其在发酵过程中应用[D]. 沈阳: 东北大学, 2011. Liu X F. Kernel optimization-based kernel principal component analysis algorithm and their applications in fermentation process[D]. Shenyang: Northeastern Univerisity, 2011. |
| [16] | 徐飞. 基于混合核函数的LSSVM发酵建模[D]. 大连: 大连理工大学, 2012. Xu F. Modeling of fermentation process based on multiple kernels least squares support vector machine[D]. Dalian: Dalian University of Technology, 2012. |
| [17] | 李炜, 徐鸿飞, 倪源. 基于核函数的PLS丁苯橡胶聚合转化率软测量[J]. 传感器与微系统, 2012, 31(3): 143-146. Li W, Xu H F, Ni Y. Soft-measurement for polymerization conversion rate of SBR based on kernel function PLS models[J]. Transducer and Microsystem Technologies, 2012, 31(3): 143-146. |
| [18] | 薛欣, 贺国平. 基于多个混合核函数的SVM决策树算法设计[J]. 计算机工程与应用, 2007, 43(8): 142-144. Xue X, He G P. Designing the algorithm of SVM decision tree based on many mixture of kernels[J]. Computer Engineering and Applications, 2007, 43(8): 142-144. |
| [19] | 刘毅, 王海清, 李平. 局部最小二乘支持向量机回归在线建模方法及其在间歇过程的应用[J]. 化工学报, 2007, 58(11): 2846-2851. Liu Y, Wang H Q, Li P. Local least squares support vector regression with application to online modeling for batch processes[J]. Journal of Chemical Industry and Engineering (China), 2007, 58(11): 2846-2851. |
| [20] | 葛志强, 刘毅, 宋执环, 等. 一种基于局部模型的非线性多工况过程监测方法[J]. 自动化学报, 2008, 34(7): 792-797. Ge Z Q, Liu Y, Song Z H, et al. Local model based monitoring for nonlinear multiple mode process[J]. Acta Automatica Sinica, 2008, 34(7): 792-797. |
| [21] | 王文俊, 张军英. 基于核的类别非局保留投影[J]. 模式识别与人工智能, 2009, 22(5): 769-773. Wang W J, Zhang J Y. Kernel based class-wise non-locality preserving projection[J]. Pattem Recognition and Artificial Intelligence, 2009, 22(5): 769-773." |



