2. 江南大学物联网工程学院自动化研究所, 江苏 无锡 214122
2. Institute of Automation, School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China
1 引言
目前,化工过程的复杂性正在日益增加,对产品质量的要求也在不断提高,现代工业往往需要装备一些先进的监控系统. 然而由于某些关键质量变量的传感器价格昂贵、 可靠性差或者具有很大的测量滞后性等缺点,导致一些重要的过程变量不能实时有效地测量. 为了解决这些问题,软测量技术在工业过程领域受到了越来越广泛的关注. 在过去的十几年,基于数据驱动的软测量建模技术得到了广泛研究,用于提高产品的质量、 降低对环境的影响[1, 2]. 一些常用的线性回归的方法如偏最小二乘(partial least squares,PLS)[3]、 主成分分析(principal component analysis,PCA)[4]等能够很好地处理输入变量和输出变量之间的线性关系. 然而,输入和输出之间常常呈现非线性的关系,线性建模方法不再适用,非线性建模方法如人工神经网络(artificial neural networks,ANN)[5]、 支持向量机(support vector machine,SVM)、 最小二乘支持向量机(least squares support vector machine,LS-SVM)[6, 7, 8, 9]可以得到良好的预测精度. 虽然这些方法能够获得很好的全局泛化性能,但是工业过程常常呈现多阶段、 时变的动态特性,预测效果往往不能得到保证. 高斯过程回归(Gaussian process regression,GPR)能够基于相似准则建立局部模型,作为一种非参数概率模型[10],GPR模型不仅可以给出预测值,还可以得到预测值对模型的信任值. 因此,本文选择GPR建立软测量模型. 同时为了对过程变量进行降维,解决不同变量之间很强的相关性,利用传统的PCA方法对过程变量进行分析. 然后基于PCA模型的得分变量,建立PCA-GPR模型,该模型可以视为非线性PCA回归模型的概率形式.
化工过程呈现严重的非线性、 时变性和多阶段性. 针对多阶段性,可以通过对各个操作模式的划分,建立不同的局部模型,描述在不同操作阶段的动态特性[11, 12]. 虽然可以对化工过程的不同阶段进行有效地划分,但是在每个操作阶段,过程的时变性和设备特性可能会发生变化,这些会使软测量模型的预测性能恶化. 为了避免预测精度的降低,需要不断地更新在线预测模型.
一种基于实时学习(just-in-time learning,JITL)的方法在过程监控和提高软测量模型的性能方面得到应用,它能够很好地处理过程的时变性和非线性[13, 14, 15]. JITL方法的有效性取决于它选择相似数据建立局部模型的能力. 与传统方法所建立的全局模型不同,JITL方法所建立的模型具有局部动态结构. 传统的全局模型是离线建立的,而基于JITL方法的局部模型是在线建立的,该模型能够更好地跟踪过程当前的状态. 同时,由于JITL建立的是局部模型,因此它能更好地处理过程的非线性. 基于这些优点,本文选择JITL方法对模型进行动态更新.
本文针对典型的TE化工过程的多阶段和时变特性,用高斯混合模型(Gaussian mixture model,GMM)对输入数据进行聚类,得到不同的子数据库,每个子数据库代表不同的操作阶段. 当需要对一个新的数据进行预测时,首先辨识得到这个新的数据隶属于每个子数据库的后验概率; 然后在每个子数据库中,用JITL选择部分相似数据建立局部PCA-GPR模型. 对于不同的操作阶段,根据辨识得到的后验概率对不同局部模型的输出进行融合. 为了进一步说明本文方法的有效性,与LS-SVM建模方法进行了比较,通过仿真实验表明,基于JITL的GPR多模型建模方法具有更高的预测精度.
2 预备知识 2.1 主成分分析(PCA)给定训练数据X∈Rn×m,m是过程变量的维数,n是训练数据的数目. PCA是在X的协方差矩阵基础上实现的. 一般情况下,可以通过奇异值分解(singular value decomposition,SVD)的方法建立PCA模型. 假设PCA模型有q个主成分,X可以被分解为如下形式[16]:
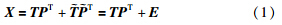
GPR[17, 18]是一种基于高斯随机函数的机器学习方法. 对于任意一个给定的输入,利用GPR可以得到关于对应输出的一个高斯分布. 给定训练样本集X∈RD×N和y∈RN,其中X=[xi∈RD]i=1,…,N,y=[yi∈R]i=1,…,N分别代表D维的输入和输出数据. 输入和输出之间的关系由式(2)产生:

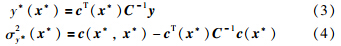
GPR可以选择不同的协方差函数c(xi,xj)产生协方差矩阵Σ,只要选择的协方差函数能保证产生的协方差矩阵满足非负正定的关系. 本文选择高斯协方差函数:
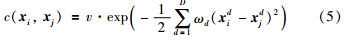
对式(4)中的未知参数v, ω1,…, ωD和高斯噪声方差σn2的估计,一般最简单的方法就是通过极大似然估计得到参数θ=[v,σn2,ω1,…,ωD]:
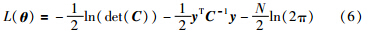
GMM是处理无监督学习的一种常用方法,如数据聚类. 在GMM中多阶段过程的数据X∈Rn×m的概率密度函数可以表示为
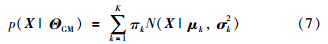
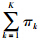 =1和0≤πk≤1.
=1和0≤πk≤1. 假设训练样本X=[xi∈Rm]i=1,…,n是独立同分布的,GMM的参数可以通过极大化如式(8)所示的似然函数获得:
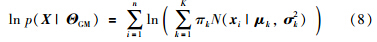
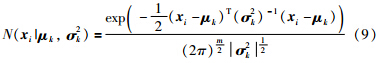
E步: 根据已有观测数据和现有模型估计缺失数据γk(xi),γk(xi)表示数据xi由第K个成分产生的概率,得到Q函数:
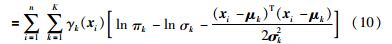
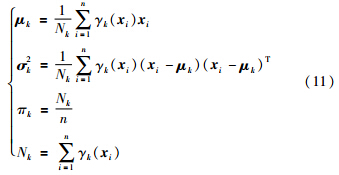
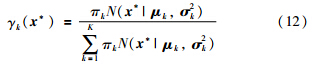
JITL可以通过建立在线局部模型实时跟踪过程的动态. 当需要对一个新的数据进行预测时,首先在数据库选择部分相似的数据,然后基于这些数据建立在线预测模型. 与单独选择欧氏距离作为相似度准则的选择数据方法相比,通过欧氏距离和角度相结合的准则确定与查询数据xq相似数据的方法具有更好的效果[20]. 本文基于JITL的相似数据的选择步骤描述如下:
Step1: 计算xq和xi之间的欧氏距离和角度:
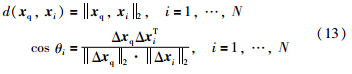
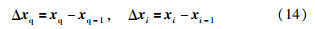
如果cos(θi)≥0,计算相似系数si:
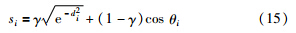
Step2: 对计算所得的所有相似系数si进行降序排列. 当建立局部模型时,只选择前L个相似系数较大的数据. 为了选择合适比例的建模数据,本文数值仿真中比例选择从10%逐渐增大到100%,最后得到最佳的数据比例为70%.
3.2 PCA-GPR模型的建立
当训练数据通过GMM聚类得到K个不同的类别时,工业过程的阶段性就确定了. 因此训练数据库可以表示成X=[X1T,X2T,…,XKT]T∈Rn×m和y=[y1T,y2T,…,yKT]T,其中Xk=[xi∈Rm]i=1,2,…,nk是第k个操作阶段的nk个训练输入数据,yk=[yi∈R]i=1,2,…,nk是相应的第k个操作阶段的输出数据,同时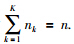 . 在建立GPR模型之前,文中采用PCA对各个操作阶段的输入变量进行预处理,从而使输入变量的维数降低. 因此,建立K个PCA模型:
. 在建立GPR模型之前,文中采用PCA对各个操作阶段的输入变量进行预处理,从而使输入变量的维数降低. 因此,建立K个PCA模型:

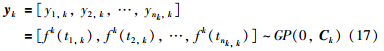
对于每个不同的阶段,PCA已经对输入变量进行了预处理. 对于一个新的输入数据x*,首先用JITL选择相似的数据建立各个操作阶段的局部模型,然后根据x*隶属于每个操作阶段的后验概率进行融合. 基于这种融合策略,无需已知x*具体隶属于哪个操作阶段,最终的预测结果也能自动产生. 本文所提出的基于JITL的多模型建模过程如图 1所示.
 |
| 图 1 基于GMM和JITL-GPR的在线多模型融合建模Fig. 1 Online multi-model combined modeling based on GMM and JITL-GPR |
为了更好地说明建模过程,建模步骤分析如下:
(1) 测量输入输出数据,组成历史训练数据库.
(2) 基于这些历史训练数据,估计GMM参数. 然后把完整的输入和输出训练数据分配到不同的操作阶段.
(3) 辨识得到的不同操作阶段对应不同的子数据库. 当一个新数据到来,计算这个新的数据隶属于每个子数据库的后验概率,后验概率最大的子数据库发生更新.
(4) 对于每个操作阶段的训练数据用PCA进行信息提取,得到K个不同的得分矩阵.
(5) 对于测试集中任意一个测试数据,不需要知道这个新的数据具体隶属于哪个操作阶段,用JITL在每个操作阶段选择最相似的数据建立各个操作阶段的局部PCA-GPR模型.
(6) 最后,对于测试数据的全局预测结果可以通过后验概率进行加权融合:
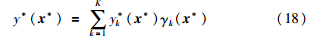
选择一个典型的化工过程——TE过程——作为仿真实验的研究对象. 为了更好地对预测结果进行比较评价,将均方根误差(RMSE)作为性能指标,评价本文建模方法的预测能力:
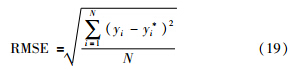
基于TE过程,Yu[21]验证了GMM和GPR用于多阶段的软测量建模的有效性和正确性. 但是,该方法所建立的模型是离线的,当过程的动态发生变化时,预测性能往往会降低,因此需要根据当前过程的动态采用一种自适应更新策略对模型进行更新. 本文采用JITL自适应策略对模型进行更新,使软测量模型能够更好地跟踪过程的动态.
TE过程是一个常见的化工过程,基于TE过程的仿真平台目前已被广泛应用于多变量控制、 软测量建模、 故障诊断等研究领域. 该过程有5个操作单元,即反应器、 冷凝器、 汽—液分离器、 循环压缩机和产品解吸塔,Yu给出了详细的过程工艺流程图[21]. 系统包括41个测量变量和12个操纵变量,在这41个测量变量中,有19个为成分变量,它们很难在线直接测得,其余22个为可以直接测得的连续操作变量. TE过程对应生产的产品中G和H的不同比率共有6种不同的操作模式,如表 1所示. 在实际生产中,会根据产品的市场需求进行模式间的切换. 本文选取22个可以实时测得的连续变量作为输入变量来预测产品流中成分A的含量[21].
| 模式 | G/H质量比 | 生产率 |
| 1 | 50/50 | 7 038 kg/h G and 7 038 kg/h H |
| 2 | 10/90 | 1 408 kg/h G and 12 669 kg/h H |
| 3 | 90/10 | 10 000 kg/h G and 1 111 kg/h H |
| 4 | 50/50 | maximum |
| 5 | 10/90 | maximum |
| 6 | 90/10 | maximum |
为了验证本文提出的多模型方法的有效性,选择前4种操作模式. 从每种操作模式中选取100组数据用于模型训练,然后再从每种操作模式中选取25组数据用于模型测试.
图 2为每个测试数据隶属于每个子数据库的后验概率,即隶属度值. 然后根据这些后验概率,无需已知当前操作阶段的具体信息,测试数据的预测输出也能够自动产生. 即使操作状态不停地发生变化,也可以对难以测得的变量进行准确地预测. 因此建立了一个自适应的模型,用于描述过程的动态和非线性.
由于每个不同操作阶段具有不同的过程动态,因此在建立局部GPR模型之前,需要用PCA对各个操作阶段的数据进行预处理. 用累计方差贡献率(cumulative percent variance,CPV)准则确定每个PCA模型主成分的数目,从而确保这些提取的主成分能够解释过程数据85%以上的信息. 本文基于PCA方法,从第1个和第3个局部PCA模型中提取出13个主成分,从第2个和第4个局部PCA模型中提取出7个主成分.
根据提取出的不同的主成分计算得到这4个PCA模型的得分矩阵,并在这4个不同的模式中,应用JITL方法进行相似数据的选择; 然后在每个操作阶段建立在线局部GPR模型; 最后根据图 2的后验概率对局部模型进行融合输出,用于对产品质量进行预测. 选择不同的相似数据比例,RMSE和CPU耗时之间的关系如图 3、 4所示. 随着数据比例的增加,计算的复杂度增加,但是预测精度也随之增加. 因此,需要选择一个合适的数据比例,本文选择70%的数据比例. 为了更好地对预测结果进行比较分析,选择LS-SVM建模方法与GPR进行比较. 这两种软测量建模方法的预测结果如图 5所示. 关于这两种建模方法的单一局部模型的预测结果如表 2和表 3所示.
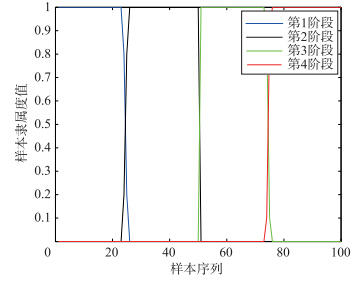 |
| 图 2 测试数据隶属于每个不同操作阶段的隶属度值Fig. 2 Membership value of each testing data samples in different operation mode |
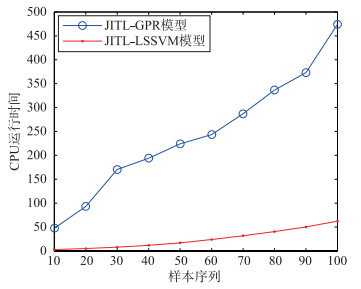 |
| 图 3 不同比例的CPU耗时Fig. 3 CPU time consuming under different sample proportion |
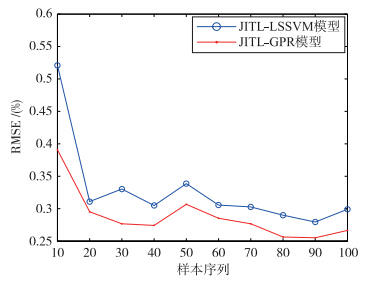 |
| 图 4 不同比例预测的RMSEFig. 4 Prediction RMSE under different sample proportion |
| 样本序列 | 第1阶段/% | 第2阶段/% | 第3阶段/% | 第4阶段/% |
| 1~25 | 0.245 0 | 2.032 6 | 4.915 0 | 6.774 0 |
| 26~50 | 3.908 6 | 0.280 4 | 7.785 8 | 4.114 8 |
| 51~75 | 1.811 1 | 4.774 9 | 0.248 3 | 9.523 4 |
| 76~100 | 5.192 5 | 2.230 0 | 9.144 0 | 0.366 0 |
| 样本序列 | 第1阶段/% | 第2阶段/% | 第3阶段/% | 第4阶段/% |
| 1~25 | 0.246 5 | 3.283 8 | 2.825 1 | 5.505 2 |
| 26~50 | 3.062 6 | 0.274 6 | 5.719 6 | 2.598 0 |
| 51~75 | 2.697 5 | 5.780 3 | 0.238 3 | 7.871 5 |
| 76~100 | 4.302 3 | 4.569 6 | 7.050 6 | 0.267 4 |
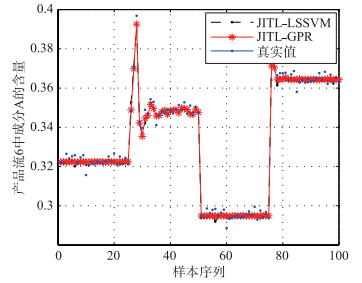 |
| 图 5 样本比例为70%时在线预测结果Fig. 5 Online prediction results of when sample proportion is 70% |
由表 2和表 3的每列可以看出,在相对应的操作阶段建立的局部LS-SVM和局部GPR模型,在这个特定的阶段具有很好的预测性能. 当所建立的局部模型被用于预测不属于这个特定阶段的数据时,软测量模型的性能会大大恶化. 同时针对于不同的操作阶段的操作特性,这两种建模方法表现出的性能也不一样. 在前两个操作阶段,这两种建模方法的精度基本一致. 但在第3个和第4个操作阶段,局部LS-SVM模型预测精度不如GPR模型,表明GPR模型能够更好地适应操作阶段的变化. 如图 4所示,JITL可以提高融合模型建立的精度(当数据比例80%和90%时),因此当每个操作阶段所建立的在线局部模型的预测结果被融合输出时,预测结果的精度和特定阶段的预测结果相似. 然而与多个单一的局部模型相比,当工业过程的操作状态发生改变时,本文所提的融合方法不需要对预测模型进行切换,说明本文所提的基于JITL的融合模型相比单一的局部模型能够更好地跟踪过程的动态.
如图 4所示,在不同的比例下,JITL-GPR都有着更好的预测精度. 而且从图 5可以清晰地看出,本文的软测量建模方法能很好地跟踪过程的动态. 由于需要综合考虑模型更新的快速性和精确性,因此选择70%的数据比例,其预测方差为0.275 3%(当数据比例为80%时,RMSE为0.256 4%).
5 结论对于具有明显阶段性、 不同动态特性和不确定性的化工过程,本文提出了一种基于JITL的在线多模型软测量建模方法. 通过应用GMM和GPR这两种方法,产生了一种非线性、 自适应的概率模型. GMM可以用来对过程的阶段性进行辨识; 然后当一个新的数据来时,在不同的操作阶段通过JITL选择相似数据构建多个局部PCA-GPR模型; 最后根据这个新的数据隶属于每个操作阶段的权重即后验概率进行融合输出. 因此,过程的动态特性、 非线性和多阶段性能够被自动地跟踪,提高了产品质量的预测精度. 采用TE过程仿真平台数据,验证了本文提出的在线多模型融合建模方法的有效性,并与LS-SVM建模方法比较,显示了本文方法具有更高的预测精度和更好的泛化性能,对具有明显阶段性特征的化工过程的动态建模研究具有一定的参考价值.
| [1] | Feil B, Abonyi J, Pach P, et al. Semi-mechanistic models for state-estimation-soft sensor for polymer melt index prediction[M]//Artificial Intelligence and Soft Computing-ICAISC 2004. Berlin, Germany: Springer-Verlag, 2004: 1111-1117. |
| [2] | Oliveira-Esquerre K A, Seborg D E, Mori M, et al. Application of steady state and dynamic modeling for the prediction of the BOD of an aerated lagoon at a pulp and paper mill: Part I, Linear approaches[J]. Chemical Engineering Journal, 2004, 104(1): 73-81. |
| [3] | Geladi P, Kowalski B R. Partial least-squares regression: A tutorial[J]. Analytica Chimica Acta, 1986, 185: 1-17. |
| [4] | Li W H, Valle-Cervantes S, Yue H H, et al. Recursive PCA for adaptive process monitoring[J]. Journal of Process Control, 2000, 10(5): 471-486. |
| [5] | Gonzaga J C B, Meleiro L A C, Kiang C, et al. ANN-based soft-sensor for real-time process monitoring and control of an industrial polymerization process[J]. Computers and Chemical Engineering, 2009, 33(1): 43-49. |
| [6] | 杨小梅, 刘文琦, 杨俊. 基于分阶段的LSSVM发酵过程建模[J]. 化工学报, 2013, 64(9): 3262-3269. Yang X M, Liu W Q, Yang J. LSSVM modeling for fermentation process based on dividing stages[J]. CIESC Journal, 2013, 64(9): 3262-3269. |
| [7] | 张倩, 杨耀权. 基于支持向量机回归的火电厂烟气含氧量软测量[J]. 信息与控制, 2013, 42(2): 258-263, 272. Zhang Q, Yang Y Q. Soft-sensor for oxygen content in flue gas of coal-fired power plant based on SVR[J]. Information and Control, 2013, 42(2): 258-263, 272. |
| [8] | 刘毅, 王海清. 采用最小二乘支持向量机的青霉素发酵过程建模研究[J]. 生物工程学报, 2006, 22(1): 144-149. Liu Y, Wang H Q. Modelling a Penicillin fed-batch fermentation using least squares support vector machines[J]. Chinese Journal of Biotechnology, 2006, 22(1): 144-149. |
| [9] | 徐飞. 基于混合核函数的LSSVM发酵建模[D]. 大连: 大连理工大学, 2012. Xu F. Modeling of fermentation process based onmultiple kernels least squares support vector machine[D]. Dalian: Dalian University of Technology, 2012. |
| [10] | Rasmussen C E, Williams C K I. Gaussian processes for machine learning[M]. Cambridge, MA, UK: The MIT Press, 2006. |
| [11] | Ge Z Q, Chen T, Song Z H. Quality prediction for polypropylene production process based on CLGPR model[J]. Control Engineering Practice, 2011, 19(5): 423-432. |
| [12] | Xiong Z, Huang G, Shao H. On-line estimation of concentration parameters in fermentation processes[J]. Journal of Zhejiang University: Science B, 2005, 6(6): 530. |
| [13] | Liu Y, Huang D, Li Y. Development of interval soft sensors using enhanced just-in-time learning and inductive confidence predictor[J]. Industrial & Engineering Chemistry Research, 2012, 51(8): 3356-3367. |
| [14] | Cheng C, Chiu M S. Nonlinear process monitoring using JITL-PCA[J]. Chemometrics and Intelligent Laboratory Systems, 2005, 76(1): 1-13. |
| [15] | Fujiwara K, Kano M, Hasebe S, et al. Soft-sensor development using correlation-based just-in-time modeling[J]. AIChE, 2009, 55(7): 1754-1765. |
| [16] | Qin S J. Statistical process monitoring: Basic and beyond[J]. Journal of Chemometric, 2003, 17(8): 480-502. |
| [17] | Bishop C M. Pattern recognition and machine learning[M]. New York, USA: Springer, 2006. |
| [18] | 雷瑜, 杨慧中. 基于高斯过程和贝叶斯决策的组合模型软测量[J]. 化工学报, 2013, 64(12): 4434-4438. Lei Y, Yang H Z. Combination model soft sensor based on Gaussian process and Bayesian committee machine[J]. CIESC Journal, 2013, 64(12): 4434-4438. |
| [19] | 何志昆, 刘光斌, 赵曦晶, 等. 高斯过程回归方法综述[J]. 控制与决策, 2013, 28(8): 1121-1129, 1137. He Z K, Liu G B, Zhao X J, et al. Overview of Gaussian process regression[J]. Control and Decision, 2013, 28(8): 1121-1129, 1137. |
| [20] | Liu Y, Chen J H. Integrated soft sensor using just-in-time support vector regression and probabilistic analysis for quality prediction of multi-grade processes[J]. Journal of Process Control, 2013, 26(6): 793-804. |
| [21] | Yu J. Online quality prediction of nonlinear and non-Gaussian chemical processes with shifting dynamics using finite mixture model based Gaussian process regression approach[J]. Chemical Engineering Science, 2012, 82: 22-30. |



