1 引言
低速EMS型磁悬浮列车作为一种城市轨道交通运输工具,具有非接触、 低噪音、 转弯半径小、 爬坡能力强等优点,近年来国内在理论研究以及工程应用中都取得了巨大的进展. 由于其具有爬坡能力强的特点,可以在城市轨道选线设计时采用坡度较大的轨道,但较大的轨道坡度给车辆悬浮控制系统带来很大的冲击,在图 1所示的南车株洲的磁浮试验线试车过程中,磁浮车在上坡和下坡时,常出现磁浮车辆砸轨的现象.
 |
| 图 1 磁浮试验线Fig. 1 Maglev test facilities |
以上文献都没有涉及到车辆速度传感器安装位置、 轨道变坡点坡度等因素对于车辆悬浮系统稳定性的影响,针对这个问题,本文通过建立简化的磁浮车—轨道系统动力学模型,对磁浮列车通过轨道变坡点时的悬浮系统稳定性问题进行了理论研究和仿真验证.
2 车辆—轨道系统模型EMS型磁浮车轨道的纵段面可分解为不同坡度、 不同长度的坡段,每节坡段的特性可以用坡段长度和坡度值来描述. 虽然为减小车辆的冲击,铁路线路设计规范中规定各坡段之间连接处的变坡点常用竖曲线来处理,但是磁浮线路在国内处于试验阶段,没有形成相应的线路设计规范,且在工程应用中由于各种原因常难以保证轨道曲线的完美; 同时在变坡点处采用竖曲线,其可由相同坡度的轨道近似替代. 不失一般性,本文采用坡度描述轨道变坡点处的线路变化情况. 另外由于车辆上坡和下坡过程中,坡度变化对于磁浮控制系统的冲击是类似的,因此本文的车—轨动力学模型主要研究列车上坡时的情况.
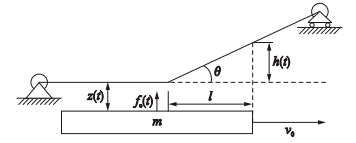
为了主要分析车辆通过变坡点时悬浮控制的稳定性问题,忽略轨道弹性形变等因素影响,本文建立简化的系统动力学模型,如图 2所示. 图 2中描述了磁浮车辆匀速从左向右经过具有一定坡度的轨道,车辆间隙传感器安装位置刚好进入变坡点时的情形. 图中fe(t)表示电磁吸力(N),m表示车体的质量(kg),z(t)表示车体的实际位移(m),h表示车体端点处轨道已经发生的位移(m),v0表示车辆的速度(km/h),θ为变坡点处轨道之间的夹角(°),tan θ=h/l为变坡点处轨道的坡度(‰),系统中参考方向取向下为正.
实际系统中由于间隙传感器不可能安装在电磁铁的最前端,所以当车体进入坡道时刻,传感器并不能马上检测到轨道曲线的变化,直到安装传感器位置处车体开始进入坡道,由间隙传感器检测气隙变化,控制系统才能对该轨道曲线变化进行动作. 间隙传感器安装位置总会带来控制系统的时滞,影响稳定性. 图 2模型中取l表示间隙传感器距离车体前端的距离(m).
 |
| 图 2 系统模型Fig. 2 The system model |
由图 2所示模型车体的垂向动力学方程分别表示为式(1),其中电磁力fe(t)常用式(2)描述.
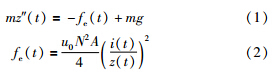
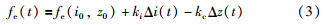
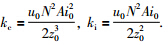 .
.虽然由于直流斩波器中存在电感,所以电流对于电压总存在滞后,但现在已有了多种成熟的电流控制方法[16],所以本文模型中直接使用电流作为控制输入. 采用工程中常用的PID算法,取悬浮间隙z、 间隙变化速度z′和加速度z″为反馈变量,取kp和kv以及ka为控制器参数,其中气隙位移反馈系数kp表征系统的悬浮刚度,气隙位移变化速度反馈系数kv可调节系统的悬浮阻尼,气隙位移加速度反馈系数ka可调节悬浮系统的惯性. 通过PID控制的电流可以表示为
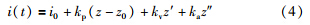
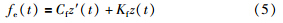
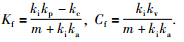 .
.联立式(1)、 式(5),令(t)=z(t)-z0得描述系统在平衡点附近运动的微分方程:
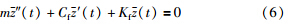
当车辆通过变坡点时,考虑如图 1所示最坏的情况. 由于气隙传感器安装位置对于控制系统产生了时滞τ=l/v0(s). 在车体前端进入变坡点处Ts之后,由于轨道曲线的变化,车—轨道之间气隙的变化速度已经变为v0·tan θ,气隙本身已经增加了h=l·tan θ,变为z0+l·tan θ,并且车体产生的电磁力不再垂直于水平方向,其垂直于水平方向的分力变为fe(t)·cos θ. 根据式(2)描述的电磁力与气隙之间平方的关系,实际作用的等效磁隙刚度与磁隙阻尼可表示为
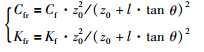


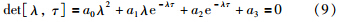
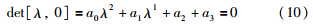
由于车辆质量m>0,等效磁隙阻尼Cf>0,坡度tan θ>0,因此条件中a0>0,a1>0总是满足的,将具体参数代入条件a2+a3>0得:
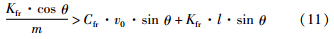
若考虑传感器时滞的影响(τ≠0),系统即使满足条件(11)也不能保证系统的稳定性. 如果τ大于某一个临界值,系统的稳定性可能会随Hopf分岔而发生变化.
方程(9)是超越方程,本身难以求得具体的解析解,应用文[17]中给出的方法,设λ=α+iβ,代入式(9)得:
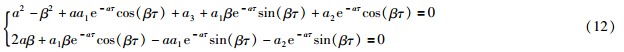
若传感器时滞对于系统稳定性有影响,式(9)中必然会出现特征值穿越虚轴的情况,此时出现共轭复根λ =±iβ. 令α=0,将λ=iβ代入式(12)有:
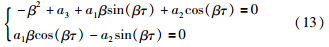
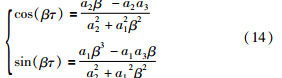
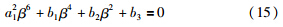
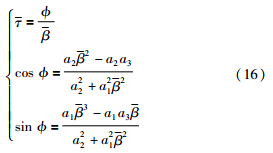
1) ∀τ∈(0,τ),系统渐进稳定.
2) τ=,τ系统处于临界状态.
3) ∀τ∈(,τ ∞),系统不稳定.
综上所述,结合条件(11)、 (16):
1)车辆通过变坡点的速度 v 0越大,式(11)右边Cfr·v0·sin θ部分越大,则系统稳定性随之变差.
2) 当变坡点处轨道坡度tan θ(取值通常为0~70‰)变大,式中cos θ变小,sin θ变大,式(11)左边变小而右边变大,系统稳定性变差.
3) 传感器安装位置离车体前端越远,l越大,式(11)右边Kfr·l·sin θ部分越大,系统稳定性变差.
4) 车体质量m 在条件式中作为分母出现,对于稳定性的影响很大,当m增大,车辆系统惯性增加,同时式(11)左边部分迅速变小,系统稳定性变差. 这也从理论上解释了试验线中当磁浮车辆重载时比轻载更容易发生砸轨现象的原因.
5) 在经过变坡点时,传感器安装位置带来的时滞会对悬浮系统稳定性造成影响,具体情况可由条件(16)判断.
6) 观察稳定条件(11),当个别参数变化时,我们可以通过调节其它的参数来维持悬浮系统稳定性. 如当车辆质量增加时,式(11)左边变小,如果能通过调节v0、 l、 θ等参数,使车辆进入变坡点时速度变慢,采用较小坡度的轨道、 调节系统等效磁隙参数等方法,使条件式右边也减小,则可以达到提高系统稳定性的目的.
4 数值仿真本文采用Simulink工具箱进行数值验证,仿真模型如图 3所示. 控制系统通过期望气隙与实际气隙值计算出需要的控制电流,由电流产生电磁力影响悬浮系统的运动. 同时轨道曲线的变化影响悬浮气隙,继而对悬浮系统的运动状态产生影响,新的运动状态由于系统时滞原因,经滞后常数时间τ=l/v0s后作为新的实际气隙值被用于计算控制电流. 仿真中系统采用的主要参数如下: 车体质量=2 000 kg,悬浮电磁铁有效面积=0.023 5 m2,悬浮电磁铁匝=350,间隙传感器距离电磁铁前端的距离=0.02 m,车辆速度=80 km/h,轨道坡度=10‰,额定悬浮间隙=0.008 m,车体在t=0.5 s时刻以匀速进入变坡点. 将PID控制系统传递函数的动态性能设计为等价二阶系统的动态性能(取阻尼系数ζ=0.5,最大超调量为5%,过渡时间为1 s),再通过经典控制理论推导出控制器相应的参数取值: ka=20,kv=500,kp=80 000.
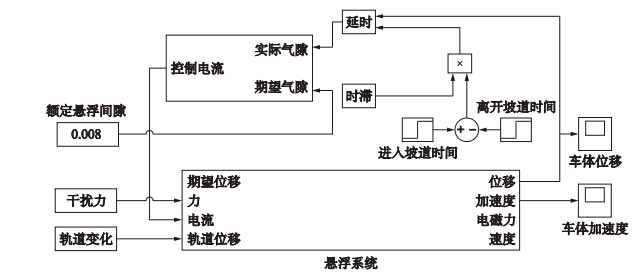 |
| 图 3 Simulink仿真图Fig. 3 Simulink simulation diagram |
在仿真1中,车辆速度分别取64 km/h、 80 km/h、 96 km/h,进入变坡点后,系统气隙位移的变化如图 4所示. 从图中可以看出,系统稳定性对于速度的变化较敏感. 在其它参数相同的情况下,随着车辆速度增快,悬浮气隙变化增大,系统稳定性变差.
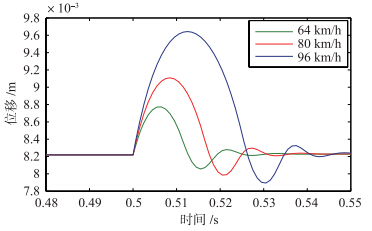 |
| 图 4 仿真1系统位移Fig. 4 Displacement in simulation 1 |
在仿真2中,轨道坡度分别取8‰、 10‰、 12‰,车辆进入变坡点后,系统气隙位移的变化如图 5所示. 从图中可以看出,系统稳定性对于轨道坡度的变化很敏感. 在其它参数相同的情况下,随着坡度增大,悬浮气隙变化快速增加,系统稳定性变差.
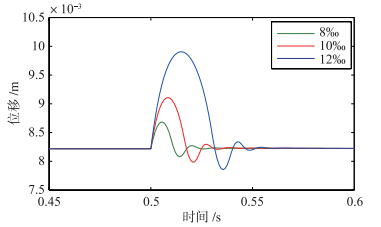 |
| 图 5 仿真2系统位移Fig. 5 Displacement in simulation 2 |
在仿真3中,间隙传感器距离电磁铁前端的距离分别取0.005 m、 0.01 m、 0.02 m,车辆进入变坡点后,系统气隙位移的变化如图 6所示. 从图中可以看出,在其它参数相同的情况下,随着安装位置远离车体前端,悬浮气隙变化增大,系统稳定性变差. 但由于传感器安装的位置物理量本身较小,其对于系统稳定性的影响没有车速和轨道坡度大.
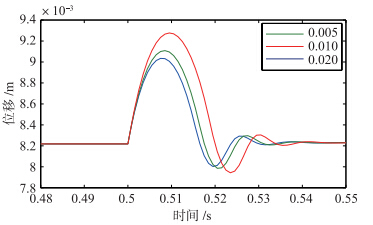 |
| 图 6 仿真3系统位移Fig. 6 Displacement in simulation 3 |
在仿真4中,车体质量分别取1 600 kg、 2 000 kg、 2 400 kg,车辆进入变坡点后,系统气隙位移的变化如图 7所示. 从图中可以看出,系统稳定性对于车体质量的变化也很敏感. 在其它参数相同的情况下,随着车体质量增大,悬浮气隙变化快速增加,系统稳定性变差.
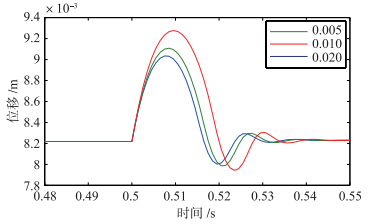 |
| 图 7 仿真4系统位移Fig. 7 Displacement in simulation 4 |
本文针对低速磁浮列车上下坡过程中出现的车辆砸轨现象,通过设计系统模型理论分析了车辆速度、 传感器安装位置、 轨道变坡点处坡度等因素对于车辆稳定性的影响.
研究表明,当车辆经过轨道变坡点时,车辆速度与轨道坡度对于系统稳定性有影响,悬浮系统稳定性随着车辆速度增加和轨道坡度变大而变差; 车体质量对系统稳定性有较大影响,质量越大,稳定性越差; 同时传感器的安装位置造成的控制系统时滞对于稳定性也有影响,并可能造成系统不稳定. 因此在一定的悬浮控制方式及相应的车—轨条件下,由于轨道坡度不能改变,为了提高系统的稳定性,车辆在上下坡时应适当减速运行,或减轻车辆载重. 通过数值仿真验证了理论分析中系统主要参数与悬浮稳定性之间关系的正确性. 结论可供磁浮车辆和轨道系统设计参考.
| [1] | 李云钢, 常文森. 磁浮列车悬浮系统的串级控制[J]. 自动化学报, 1999, 25(2): 247-251. Li Y G, Chang W S. Cascade control of an EMS maglev vehicle's levitation control system[J]. Acta Automatica Sinica, 1999, 25(2): 247-251. |
| [2] | 王莉, 张昆仑. 基于零功率控制策略的混合磁悬浮系统[J]. 西南交通大学学报, 2005, 40(5): 667-672. Wang L, Zhang K L. Hybrid magnetic suspension system based on zero power control strategy[J]. Journal of Southwest Jiaotong University, 2005, 40(5): 667-672. |
| [3] | 刘恒坤, 郝阿明, 常文森. 磁浮列车的非线性解耦控制[J]. 铁道学报, 2009, 31(1): 46-50. Liu H K, Hao A M, Chang W S. Nonlinear decoupling control of maglev train[J]. Journal of the China Railway Society, 2009, 31(1): 46-50. |
| [4] | 邹东升, 佘龙华, 常文森. 抑制磁浮系统车轨耦合振动的自适应陷波滤波器设计[J]. 信息与控制, 2009, 38(2): 234-238. Zou D S, She L H, Chang W S. Design of adaptive notch filter to suppress coupled vibration of maglev vehicle and guideway system[J]. Information and Control, 2009, 38(2): 234-238. |
| [5] | 张锟, 崔鹏, 李杰. 磁悬浮系统的加速度计反馈控制算法[J]. 控制理论与应用, 2009, 26(9): 988-992. Zhang K, Cui P, Li J. Accelerometer feedback control algorithm for maglev system[J]. Control Theory & Applications, 2009, 26(9): 988-992. |
| [6] | Gentili L M. Robust nonlinear disturbance suppression of a magnetic levitation system[J]. Automatica, 2003, 39(4): 735-742. |
| [7] | 翟婉明, 赵春发. 磁浮车辆/轨道系统动力学(I)——磁/轨相互作用及稳定性[J]. 机械工程学报, 2005, 41(7): 1-10. Zhai W M, Zhao C F. Dynamics of maglev vehicle/guideway sysystems(I) - magnet/rail interaction and system stability[J]. Chinese Journal of Mechanical Engineering, 2005, 41(7): 1-10. |
| [8] | 施晓红, 龙志强. 磁悬浮车轨耦合控制系统的非线性振动特性分析[J]. 铁道学报, 2009, 31(4): 38-42. Shi X H, Long Z Q. Nonlinear vibration analysis of the maglev guideway-vehicle coupling control system[J]. Journal of the China Railway Society, 2009, 31(4): 38-42. |
| [9] | 梁鑫, 罗世辉, 马卫华, 等. 磁浮列车单铁悬浮车桥耦合振动分析[J]. 交通运输工程学报, 2012, 12(2): 32-37. Liang X, Luo S H, Ma W H, et al. Coupling vibration analysis of single-magnet suspension vehicle-bridge for maglev train[J]. Journal of Traffic and Transportation Engineering, 2012, 12(2): 32-37. |
| [10] | Zhou D F, Hansen C H, Li J. Suppression of maglev vehicle-girder self-excited vibration using a virtual tuned mass damper[J]. Journal of Sound and Vibration, 2011, 330(5): 883-901. |
| [11] | 罗昆, 尹力明, 谢云德. 中低速磁悬浮列车线路选线参数分析——坡度值计算与分析[J]. 机车电传动, 2004(4): 17-19. Luo K, Yin L M, Xie Y D. Analysis on location parameters of line for mid and low speed maglev train-calculation and analysis of gradient[J]. Electric Drive for Locomotives, 2004(4): 17-19. |
| [12] | 李云钢, 常文森, 张鼎. EMS型磁浮列车悬浮控制系统对爬坡能力的约束分析[J]. 国防科技大学学报, 2005, 27(4): 106-109. Li Y G, Chang W S, Zhang D. The analysis of levitation control system's restriction on the grade ability of EMS maglev[J]. Journal of National University of Defense Technoloy, 2005, 27(4): 106-109. |
| [13] | 刘恒坤, 张晓. 一种适应轨道曲线变化的磁悬浮控制算法[J]. 系统仿真学报, 2010, 22(5): 1101-1105. Liu H K, Zhang X. Maglev control algorithm adapted to variety of track curve[J]. Journal of System Simulation, 2010, 22(5): 1101-1105. |
| [14] | 胡立成, 蔡俊. 高速磁浮线车站内线路主要技术标准的探讨[J]. 城市轨道交通研究, 2013, 16(6): 65-68. Hu L C, Cai J. On the selection of maximum transverse gradient of high-speed maglev line[J]. Urban Mass Transit, 2013, 16(6): 65-68. |
| [15] | 张耿, 李杰. 低速磁浮列车竖曲线电磁力计算[J]. 中国电机工程学报, 2012, 32(3): 150-156. Zhang G, Li J. Calculation of electromagnetic force of low-speed maglev on a vertical curve[J]. Proceedings of the CSEE, 2012, 32(3): 150-156. |
| [16] | 张东升, 梅雪松, 郝晓红, 等. 磁悬浮系统的电流控制方法[J]. 西安交通大学学报, 2007, 41 (9): 1096-1100. Zhang D S, Mei X S, Hao X H, et al. Current control method for magnetic suspension system[J]. Journal of Xi'an Jiaotong University, 2007, 41(9): 1096-1100. |
| [17] | 廖晓昕. 稳定性的理论、方法和应用[M]. 第二版. 武汉: 华中科技大学出版社, 2010: 196-205. Liao X X. Theory methods and application of stability[M]. 2nd ed. Wuhan: Huazhong University of Science & Technology Press, 2010: 196-205." |



