2. 吉林大学通信工程学院, 吉林 长春 130022
2. College of Comanuni Cation Engineering, Jinlin University, Changchun 130022, China
1 引言
由于自主车辆具有比人类驾驶员反应速度快、 控制精度高、 处理突发问题能力强等优点，因此可以大大减少交通事故的发生[1]. 而车辆自主地完成各项指定任务时，都必须解决最基本且最重要的轨迹跟踪控制问题[2]. 车辆系统是一个高度耦合的复杂非线性系统，实际上存在着相当多的不确定性因素[3, 4]，这会对控制器性能产生严重影响. 因此，在不确定性因素影响下的轨迹跟踪控制问题已成为各国学者研究的热点.
对于轨迹跟踪问题，不同研究者采用的方法也不尽相同. 传统的二自由度模型形式简单且能够反应车辆的基本特性，因此，基于该模型开发出了很多的控制方法. Hayakawa等[5]针对智能交通系统中的车辆路径跟踪问题进行了研究，设计了基于PID控制的反馈加前馈控制器，实现车辆在速度变化时的自动光滑转向. Tomizuka教授[6]根据该模型设计了基于预瞄的最优侧向控制器，提高了跟踪曲线的精度和性能，推动了车辆横向控制的发展. 文[7]采用基于线性矩阵不等式(linear matrix inequality，LMI)的状态反馈控制方法，设计了车辆横向控制器. Falcone等[8]采用三自由度非线性整车模型来预测智能车辆行驶轨迹，但车辆的状态变量对计算效率有很大的制约性. Trabia[9]采用模糊控制策略设计横向控制系统，但隶属度函数参数和控制规则参数主要靠试探法或专家经验法来确定，主观性较强且容易产生稳态误差.
综上，车辆模型从线性到非线性取得了很大进步，但在模型线性化的过程中并未考虑简化引起的未建模动态. 而车辆在实际运行过程中，未建模动态会对控制器的性能产生严重影响. 随着人们对车辆控制精度要求的提高，对未建模动态的考虑及处理愈为重要. 本文将对简化为线性二自由度的车辆模型进行研究，同时充分考虑简化过程中可能产生的未建模动态. 并基于随机模型预测控制算法计算出期望的方向盘转角并作为实际车辆的控制输入，实现车辆的侧向轨迹跟踪控制. 为探究未建模动态的影响，在相同的工况下设计了两组控制器进行比较，并采用专业的车辆动力学软件veDYNA进行仿真并验证控制器的有效性.
2 车辆动力学建模实际车辆是一个复杂系统，为了便于控制器的设计，常常将模型进行简化. 简化过程会有很多动态特性的丢失，我们将丢失的这部分特性定义为未建模动态[10]. 本文基于简化的车辆二自由度模型设计轨迹跟踪控制器. 首先做如下假设[11]：
(1) 忽略转向系统中非线性的影响，把车辆的方向盘转角作为系统直接的控制输入，并且认为左右轮的侧偏角和转角输入相同.
(2) 忽略悬架作用，认为车辆只在x-y平面内运动.
(3) 在所建立的坐标系中沿x轴的车辆速度u不变.
(4) 忽略空气阻力和滚动阻力.
基于以上假设实际车辆便可简化成一个两轮自行车模型，如图 1所示.
 |
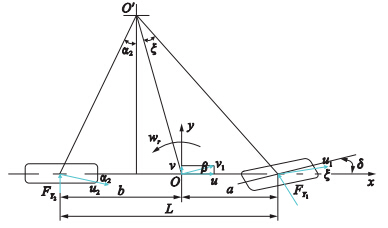| 图 1 二自由度车辆模型Fig. 1 Two degrees of freedom(DOFs)of vehicle dynamics model |
为了便于理解，将公式中涉及到的符号含义以表 1的形式表示出来.
| 参数 | 含义 |
| a、 b | 质心到前、 后轴的距离 |
| m | 车辆质量 |
| u | 纵向速度 |
| r | 横摆角度速度 |
| k1、 k2 | 前后轮胎的侧偏刚度 |
| β | 质心侧偏角 |
| FY1、 FY2 | 前后轮的轮胎力 |
| δf | 前轮转角 |
| φ | 横摆角 |
| α1、 α2 | 前后轮胎侧偏角 |
根据牛顿定律，建立车辆动力学方程如下：
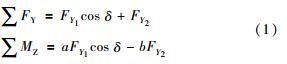
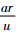-δf，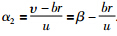
. 为简化该模型做如下近似，β≈tan β=
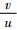，ξ≈tan ξ=
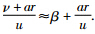. 综上可以列出考虑侧向及横摆运动在内的车辆动力学方程为
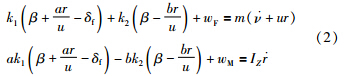
将车辆的侧向位移设为一个状态变量，根据车辆坐标系与大地坐标系的位移转换关系可得[12]：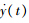 
=usin φ+νcos φ. 又由于汽车行驶在路线较直或者弯曲程度不大的高速公路上φ较小[13]，则有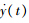=uφ+uβ+wY，设wY是上述简化过程引入的未建模动态.
取[β r φ y]T为状态变量，令w=[wFwMwY]T，将前轮转角δf作为模型的控制输入，整理后可得考虑未建模动态的线性二自由度车辆模型的状态空间表达式如下
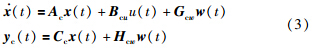
(1) 假设w的3个分量为相互独立且同分布的随机变量.
(2) 假设相同的分布都满足
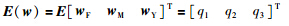
完整的自主车辆规划与控制系统基本上由3部分组成： 行为决策、 规划以及控制. 行为决策和规划模块根据自主车辆的驾驶行为意图，并结合环境及车辆行驶的状态信息，规划出期望的行驶轨迹. 由于本文的主要内容是对车辆的侧向轨迹进行跟踪即控制模块，故对前两部分内容不做介绍. 轨迹跟踪是指在已知参考轨迹的前提下，设计相应控制率即控制输入，控制车辆在不同的车速、 道路信息和行驶工况等条件下，仍能完成最终的控制目标，也就是车辆的转向控制[15]，控制框图如图 2所示. 根据当前的状态预测出下一个预测时域内车辆的侧向位移，再进行比较和优化，求解出期望的前轮转角δf. 经过一个转向角传动比增益G后得到方向盘转角序列，将序列的第一个元素作用到车辆，车辆输出侧向位移的同时又会得到新的状态. 然后重复上述过程，直至实现最终的控制目标.
 |
| 图 2 轨迹跟踪控制系统框图Fig. 2 Block diagram of trajectory tracking control system |
根据模型预测控制原理与自主驾驶车辆操控行为的一致性，采用模型预测控制思想来实现车辆的侧向轨迹跟踪. 首先，将模型(3)采用零阶保持的方法离散化，离散周期为Ts，得到离散化后的模型为
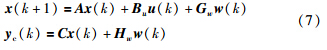
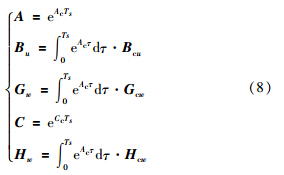
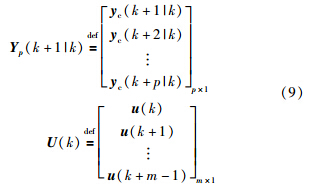
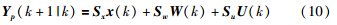
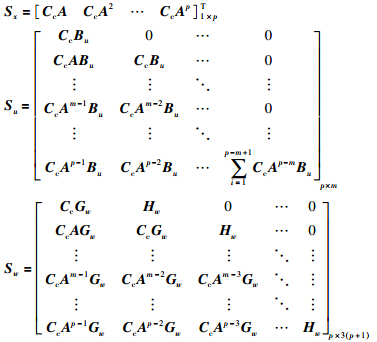
根据性能需求要求满足轨迹跟踪精度的同时希望执行器的控制动作不要过大，由于预测方程表达式中存在随机变量，因此，可以选择如下的目标函数：
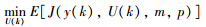
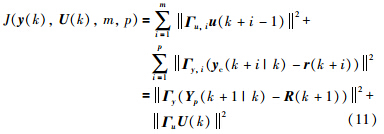
控制系统的稳定性分析是设计和实现控制系统的先决条件. 根据前文论述，被控系统可以描述为式(7)的形式，将控制律代入到状态空间方程式(7)，得到闭环系统为
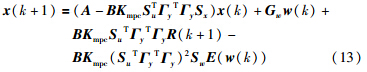
选取相同的测试工况，通过对比基于veDYNA软件的HQ430模型在该控制器作用下输出的状态与红旗HQ430实车的输出状态来验证本文提出的控制算法的有效性. 验证方案如图 3所示.
 |
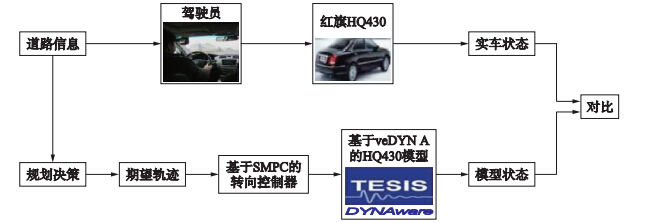| 图 3 基于红旗HQ430实车数据的验证方案Fig. 3 scheme based on Hongqi HQ430 vehicle data |
为了验证控制器的有效性，需要进行实车实验，但是考虑到安全性、 可靠性和经济性等因素，目前直接在红旗HQ430轿车上测试的实验条件还不具备. 因此，采用基于veDYNA软件的HQ430模型作为控制器的被控对象. 红旗HQ430模型是采用veDYNA软件结构并匹配红旗HQ430轿车相应参数，基于实车实验数据获得的完整的仿真动力学模型[18]. 经过实验验证得到该模型的纵向动力学平均精度为91.3％. 侧向动力学平均精度为79.4％，从而说明建立的车辆仿真动力学模型在一定程度上可代替真实车辆用于仿真研究.
上述验证方案中参与测试的驾驶员在清洁、 干燥、 平直的沥青路面，以v=64 km/h的速度行驶双移线轨迹，并利用传感器记录行驶的相关信息. 为了验证控制器的控制效果，将红旗HQ430实车的状态与基于veDYNA软件的HQ430模型在该控制器作用下输出的状态进行对比，对比结果如图 4所示. 红旗HQ430用于控制器设计的参数及实验工况的其它信息分别如表 2和表 3所示.
| 参数 | 数值 |
| m | 2 160 kg |
| a | 1.5 m |
| b | 1.25 m |
| Iz | 3 411 kg·m2 |
| k1 | -137 920 N/rad |
| k2 | -87 594 N/rad |
| 期望的轨迹 | 红旗HQ430轿车测试的双移线 |
| 车辆的速度 | v=64 km/h |
| 路面的摩擦系数 | μ=1 |
| 控制器的参数 | Γy=0.3×Ip×p，Γu=1.5×Im×m |
| 是否考虑未建模动态的影响 | 考虑 |
| 注： I是单位矩阵. | |
 |
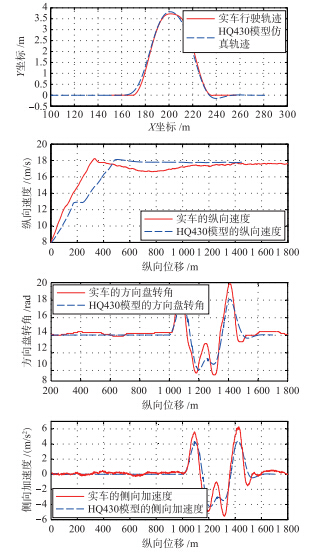| 图 4 基于红旗HQ430模型的双移线跟踪实验Fig. 4 Double lane change tracking experiment based on Hongqi HQ430 model |
由实验结果可知，红旗HQ430模型输出的仿真轨迹与实车红旗HQ430输出的轨迹重合度较高，但模型输出的状态并没有与实车输出的状态完全重合. 原因可能是传感器存在误差、 基于veDYNA软件的HQ430车辆动力学模型与实车之间存在差异以及实车在行驶过程中受到风阻的影响等. 但状态的大致趋势相同、 幅值也都相差不大，因此，该控制器在理论上能够应用到实车.
4.2 基于veDYNA软件的仿真测试HQ430模型是基于实车实验数据获得的仿真动力学模型，为更进一步验证控制器的控制效果，我们将被控对象换成高精度的基于veDYNA软件的车辆并进行离线仿真.
基于veDYNA软件的完全非线性、 参数化的高精度车辆动力学模型主要包括以下几个部分： 底盘(包括车身和桥)、 前后桥的运动学关系、 转向系统、 传动系统、 发动机、 变速器和轮胎模型[19]，被广泛地用于算法离线仿真、 快速控制原型和硬件在回路中的仿真. 因此，采用基于veDYNA软件的limousine(Light)整车模型作为被控对象，采用的参数如表 4所示. 通过不同工况下的实验，分析车辆模型输出的状态，验证MPC控制器在车辆轨迹跟踪控制研究中的可行性和有效性.
| 参数 | 数值 |
| m | 1 296 kg |
| a | 1.25 m |
| b | 1.5 m |
| Iz | 1 750 kg·m2 |
| k1 | -100 700 N/rad |
| k2 | -86 340 N/rad |
期望轨迹选择标准蛇形穿杆实验下的轨迹，实验工况的具体信息如表 5所示. 记录跟踪的结果和车辆的状态如图 5所示，结果表明，在该工况下也可以实现很好的跟踪控制.
| 期望的轨迹 | 标准蛇形穿杆实验下的轨迹 |
| 车辆的速度 | v=60 km/h |
| 路面的摩擦系数 | μ=1 |
| 控制器的参数 | Γy=1×Ip×p，Γu=0.8×Im×m |
| 是否考虑未建模动态的影响 | 考虑 |
| 注： I是单位矩阵. | |
 |
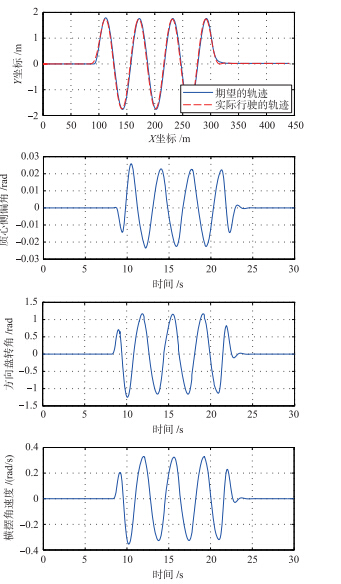| 图 5 标准蛇形穿杆实验Fig. 5 Standard serpentine wear bar experiment |
为了验证建模过程中由于模型简化而引起的未建模动态的影响，对比实验3和实验4，并分别对确定MPC与随机MPC展开研究. 被控对象仍然选样基于veDYNA软件的limousine(Light)整车模型.
实验3的期望轨迹具体数据如图 6所示，设道路的摩擦系数为0.4，车辆加速时间为1 s.
 |
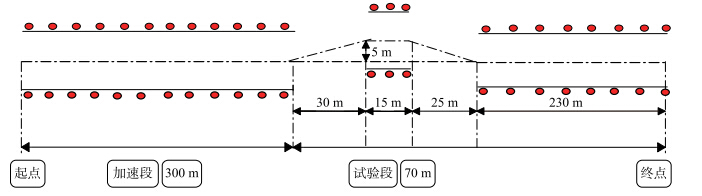| 图 6 实验道路数据Fig. 6 The data of the experimental road |
不断改变自主车辆的纵向速度，将跟踪误差的结果以标准差的形式表示出来，实验数据结果如表 6所示.
| 车辆速度 | 无补偿作用跟踪误差的标准差 | 有补偿作用跟踪误差的标准差 |
| v=30 km/h | 0.266 6 | 0.254 8 |
| v=40 km/h | 0.149 4 | 0.148 0 |
| v=50 km/h | 0.127 8 | 0.094 1 |
| v=60 km/h | 0.117 8 | 0.107 4 |
由表 6可知，当车辆运行在相同的工况下，车辆速度不同跟踪误差的标准差也不相同，但对比相同速度下两种控制器的作用可以发现，有补偿的控制器的跟踪误差的标准差要小于不考虑未建模动态补偿的控制器的跟踪误差的标准差. 为进一步掌握车辆行驶的状态，图 7列出了车辆速度v=50 km/h的轨迹跟踪结果及车辆的一些状态.
由图 7可知，考虑未建模动态的控制器在双移线的尖峰时刻可以实现更小的跟踪误差，但在最后趋于平稳的过程中，两种控制器在时间上的效果几乎是相同的. 只不过考虑未建模动态的控制器振动的幅度更小. 除了在一些特殊时刻的状态偏差比较明显以外，其余时刻车辆状态曲线的大致趋势是相同的.
 |
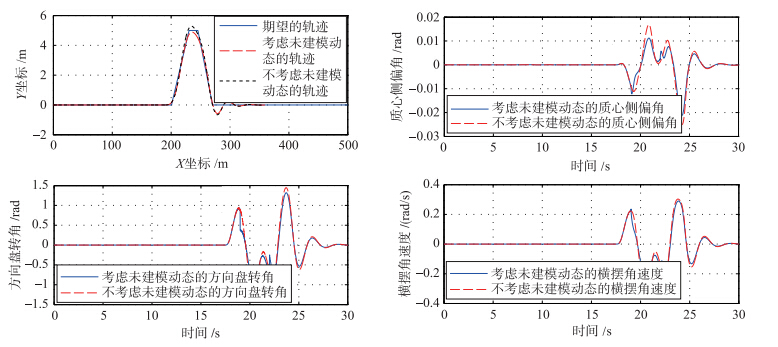| 图 7 双移线跟踪实验Fig. 7 Double lane change tracking experiments |
类比实验3，实验4期望轨迹选择标准双移线，摩擦系数μ=1，记录数据如表 7所示.
| 车辆速度 | 无补偿作用跟踪误差的标准差 | 有补偿作用跟踪误差的标准差 |
| v=80 km/h | 0.221 9 | 0.213 0 |
| v=90 km/h | 0.136 3 | 0.131 5 |
| v=100 km/h | 0.099 1 | 0.090 9 |
| v=110 km/h | 0.100 6 | 0.088 8 |
| v=120 km/h | 0.130 2 | 0.093 9 |
车辆速度v=100 km/h的轨迹跟踪结果及车辆的状态如图 8所示.
 |
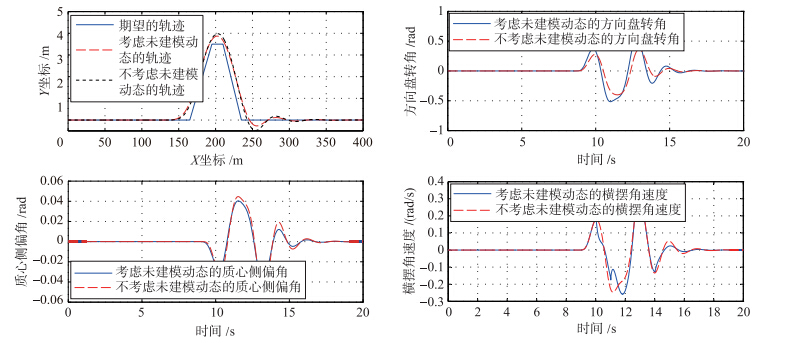| 图 8 标准双移线跟踪实验Fig. 8 Standard double lane change tracking experiments |
观察实验4的结果可以得到与实验3一致的结论： 相同工况下，考虑未建模动态的控制器可以更高精度地实现车辆的轨迹跟踪控制. 但对比车辆状态可知，考虑未建模动态的补偿作用虽然可以实现更高精度的轨迹跟踪控制，但是补偿作用也会对车辆的状态产生影响. 原因可能是在对未建模动态进行处理时将随机变量取期望，仿真过程中发现wF、 wM对控制器的影响很小，能实现很大程度补偿作用的就是wY. 而wY是车辆在位移转换过程引起的，对它补偿只能从更精确地跟踪侧向轨迹的角度出发，而这个过程并未考虑到车辆的状态，强行地补偿车辆轨迹. 由仿真曲线可知，在提高精度的同时，车辆的质心侧偏角等参数都在合理的范围内[20]，也就是说，虽然有起伏但车辆的状态仍然是稳定的. 因此，可以说考虑了未建模动态设计的控制器可以更好地实现车辆的侧向轨迹跟踪.
5 结论本文着重研究了基于随机模型预测控制的车辆轨迹跟踪这一热点问题. 在借鉴传统车辆二自由度模型的基础上，对简化过程的未建模动态进行补偿，通过与已有轨迹跟踪控制算法的对比，最终选择对非线性、 约束具有较好处理能力的MPC算法设计控制器. 为了研究未建模动态的影响，最后设计了一系列对比实验，充分验证了考虑未建模动态设计控制器的必要性.
| [1] | 黄岩, 吴军, 刘春明, 等. 自主车辆发展概况及关键技术[J]. 兵工自动化, 2010, 29(11): 8-13, 26. Huang Y, Wu J, Liu C M, et al. Overview and key technologies of autonomous vehicles[J]. Ordnance Industry Automation, 2010, 29(11): 8-13, 26. |
| [2] | 唐飞云. 自主导航车轨迹跟踪控制方法研究[D]. 大连: 大连理工大学, 2012. Tang F Y. Trajectory tracking control method for an autonomous guided vehicle[D]. Dalian: Dalian University of Technology, 2012. |
| [3] | 史先鹏, 刘士荣. 机械臂轨迹跟踪控制研究进展[J]. 控制工程, 2011, 18(1): 116-122. Shi X P, Liu S R. A survey of trajectory tracking control for robot manipulators[J]. Control Engineering of China, 2011, 18(1): 116-122. |
| [4] | 曹凯, 于善义, 于少伟. 基于多隐马尔可夫模型的车辆机动行为识别与预测[J]. 信息与控制, 2014, 43(4): 506-512. Cao K, Yu S Y, Yu S W. Maneuver behavior identification and prediction for vehicles based on multi-hidden markov model[J]. Information and Control, 2014, 43(4): 506-512. |
| [5] | Hayakawa Y, White R, Kimura T, et al. Driver-compatible steering system for wide speed-range path following[J]. IEEE/ASME Transactions on Mechatronics, 2004, 9(3): 544-552. |
| [6] | Peng H, Tomizuka M. Preview control for vehicle lateral guidance in highway automation[J]. Journal of Dynamic Systems, Measurement and Control Transactions of the Asme, 1993, 115(4): 679-686. |
| [7] | Enache N M, Mammar S, Netto M, et al. Driver steering assistance for lane-departure avoidance based on hybrid automata and composite Lyapunov function[J]. IEEE Transactions on Intelligent Transportation Systems, 2010, 11(1): 28-39. |
| [8] | Falcone P, Borrelli F, Asgari J, et al. Predictive active steering control for autonomous vehicle systems[J]. IEEE Transactions on Control Systems Technology, 2007, 15(3): 566-580. |
| [9] | Trabia M B, Shi L Z, Hodge N E. A fuzzy logic controller for autonomous wheeled vehicles[M]//Mobile Robots, Moving Intelligence. Berlin, Germany: Springer, 2006: 176-200. |
| [10] | 彭昕. 具有未建模动态系统的自适应控制[D]. 成都: 西南交通大学, 2010. Peng X. Adaptive control of system with unmodeled dynamics[D]. Chengdu: Southwest Jiaotong University, 2010. |
| [11] | 余志生. 汽车理论[M]. 北京: 机械工业出版社, 2009. Yu Z S. Elementary vehicle dynamics[M]. Beijing: Mechanical Industry Press, 2009. |
| [12] | Setlur P, Wagner J R, Dawson D M, et al. A trajectory tracking steer-by-wire control system for ground vehicles[J]. IEEE Transactions on Vehicular Technology, 2006, 55(1): 76-85. |
| [13] | 刘志强, 李伟强. 基于驾驶员视角的汽车行驶轨迹跟踪模型[J]. 农业机械学报, 2007, 38(7): 35-38. Liu Z Q, Li W Q. Driver model based on driver's heading angle[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(7): 35-38. |
| [14] | 周聪. 基于非线性估计理论的线控转向汽车状态估计研究[D]. 成都: 西南交通大学, 2012. Zhou C. Research on vehicle state estimation with steer-by-wire system based on nonlinear estimation method[D]. Chengdu: Southwest Jiaotong University, 2012. |
| [15] | 任佳星. 基于免疫算法的智能车辆运动控制研究[D]. 太原: 中北大学, 2012. Ren J X. Research on intelligent vehicle motion control based on immune algorithm[D]. Taiyuan: North Central of China, 2012. |
| [16] | Ji Y, Guo H Y, Chen H. Integrated control of active front steering and direct yaw moment based on model predictive control[C]//The 26th Chinese Control and Decision Conference (CCDC). Piscataway, NJ, USA: IEEE, 2014: 2044-2049. |
| [17] | 陈虹. 模型预测控制[M]. 北京: 科学出版社, 2013. Chen H. Model predictive control[M]. Beijing: Science Press, 2013. |
| [18] | 张华玉. 自主驾驶车辆速度及道路坡度估计研究[D]. 长春: 吉林大学, 2013. Zhang H Y. Estimate road grade and velocity for autonomous driving vehicle[D]. Changchun: Jinlin University, 2013. |
| [19] | 北京九州恒润科技有限公司. Tesis DYNAware——基于Matlab/Simulink的车辆动力学实时仿真模型[J]. CAD/CAM与制造业信息化, 2004(3): 72-74. Beijing Jiuzhouhengrun Science and Technology Co., Ltd. Tesis DYNAware - real-time vehicle dynamics simulation model based on Matlab/Simulink[J]. CAD/CAM Yu Zhizhaoye Xinxihua, 2004(3): 72-74. |
| [20] | 周红妮. 车辆稳定性控制方法与策略的比较研究[D]. 武汉: 武汉科技大学, 2006. Zhou H N. The comparison research on control method and strategy of vehicle stability[D]. Wuhan: Wuhan University of Science and Technology, 2006. |