2. 华南师范大学, 广东 广州 510631
2. South China Normal University, Guangzhou 510631, China
1 引言
人脸识别一直是计算机视觉与模式识别研究的主要内容之一,抽取有效特征是提高识别效果的关键问题. 模式识别的一个主要任务是从给定的模糊图像中推断对目标的描述,图像信息并不具备明确从属而是具有模糊特性,因此很难确认该图像是否明确符合某种概念. 人脸图像的模糊效应通常是由于环境光照变化和目标的相对运动等原因造成的. 由于这些因素是不可避免的,因此,图像形成过程中存在模糊是必然的,分析模糊对图像的影响是图像处理的一个重要方面.
在人脸识别中,模糊图像可以表示为源图像的强度y和模糊点扩散函数k的卷积:
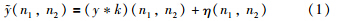
去模糊的目的在于从模糊图像转换到清晰图像y. 在已知模糊基的所有信息的条件下,由式(1)求逆可以得到y. 因为噪声的未知性,由式(1)求逆得到y难度较大,受限于图像采集对象不配合以及遮挡、 姿态、 光照、 异质模态等采集环境变化的影响,完全获取模糊基的信息是不可能的. 在图像恢复技术的研究中,具有代表性的方法包括: 盲反卷积和非盲反卷积方法[1, 2]、 基于全变差的正则化方法和Tikhonov正则化方法等[3, 4],这些方法被广泛应用于模糊人脸图像的识别中[5, 6].
相比较而言,基于模糊不变量的直接方法是通过给定图像模糊不变量来识别图像模糊情况. 该方法提取模糊不变量作为特征描述算子,为后续的图像处理任务提供信息. 主要思路: 假设yF、 yF、kF分别表示为模糊图像,清晰图像y和模糊点扩散函数k的傅里叶变换(discrete Fourier transform,DFT). 在无噪声的条件下,式(1)可以表示为

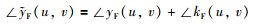
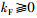 ),使得:
),使得:
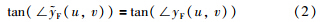
利用模糊基之间过渡矩阵的特性,本文提出一种基于模糊不变量的直接方法,与传统方法的区别是: 该模糊基由张成的空间中正交基的线性组合而成. 并定义了一种新的模糊不变量,可处理多种模糊类型,该模糊不变量可看作格拉斯曼流型中的一个点,这是一种基于微分几何学,对于不变量张成空间的新的理解. 通过实际应用测试数据表明: 利用新算法进行的模糊人脸图像识别冗余信息较少且其描述能力和鲁棒性更佳,较已有方法具有明显优势.
2 模糊量和模糊不变量的空间为了去模糊化,需要得到图像y关于任意模糊点扩散函数k的不变量,给定假设条件: 系统中不存在噪声,在已知模糊基的最大尺寸的条件下,模糊形变过程可以近似为理想图像和一个任意中心对称的点扩展函数卷积的过程,未知的模糊点扩散函数(PSF)对应的BTTB(block toeplitz toeplitz block)矩阵是满秩的,该矩阵对中心对称点扩散函数造成的模糊图像具有不变性,在计算过程中不存在离散近似误差和坐标变换误差,故在有噪声和无噪声情况下均具有更好的模糊不变性.
对于二维信号,将平方可积、 尺寸为b1×b2的模糊点扩散函数k表示为

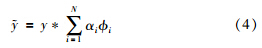
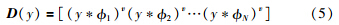
由此可得: 列空间span(D(y))是y的模糊不变量,也就是: span(D (y))=span(D(y)),从而可得D(y)和D(y)等价.
该方法优点体现在: 1) 基函数能够张成任意具有最大已知尺寸的模糊函数空间,无需对模糊函数的形状作任何限制. 2) 虽然部分模糊PSF是不可逆的,其BTTB矩阵通常是满秩矩阵,具有很大的条件数,但是利用正交矩阵等价类集合的方法无需计算矩阵的逆,因此可不考虑模糊方法中条件数过大导致的不确定性.
3 模糊人脸图形识别考虑建立一个包含M个个体的图像库,M为正交矩阵等价类集合,其中{yi}i=1M表示人脸图形库,包含所有清晰和模糊图像的个体. 采用具有电子探针的数字成像系统,用自适应变间距采样方式逐点成像,获取数字电子探针图像,为其中一个模糊探针图像,在给定yi、 的条件下,找出模糊探针图像属于哪一个个体. 根据人脸图形库和探针图像建立各自的字典D(yi)、 D(y),比较其列张成的空间即可进行人脸图像识别[10, 11].
3.1 格拉斯曼流型的定义和识别方法根据定义,流形是一种拓扑空间,其局部与欧氏空间相似. 假设样本均匀采集于d=d1×d2(d>N)维欧氏空间中的N维流形上,格拉斯曼流型GN,d是d×N正交矩阵等价类集合. 格拉斯曼上的点是Rd的N维子空间,格拉斯曼流型是所有的Rd线性子空间的空间. 格拉斯曼流型GN,d可直观解释为空间Rd中所有N维线性子空间的集合,GN,d上的每个点是一个d×N维正交矩阵列空间所张成的子空间. 针对格拉斯曼的一组点{Y1,Y2,Y3,…,Yn},并给出每对点的相似度比较,将所有点划分成群组,这样同一组中的点是相似的,而不同组内的点不相似. 依据流形假设,如果数据点之间有边连接,则被投影到低维流形时,数据点依然保持近邻. 模糊不变量Y是GN,d中的一个点,如图 1所示. 文[12, 13]中描述了格拉斯曼流型的几何特点,这些几何特征已经应用到具有子空间限制的识别问题中[14, 15]. 利用格拉斯曼核度量子空间的相似度,实现格拉斯曼流型上数据非线性判别分析,通过非线性变换把格拉斯曼流型上松散分布的样本压缩到低维的格拉斯曼流型中,使样本分布更紧凑、 更易于分类,降低计算的复杂度. 如计算模糊不变量之间的距离,可利用点与点之间的距离来进行分类,将图像库中每一个人隶属于某一个图像,则两个子空间的黎曼距离是连接格拉斯曼流型的两个点的最短距离; 通过计算方向矩阵A,得到起点Y1、 终点Y2的测量线,其中A可通过逆指数映射,其长度表示了格拉斯曼流型上两点之间的距离dG. 采用投影核来表示格拉斯曼流型上两点之间的距离,将tr(AAT)作为计算长度的一个度量,AY1,Y2表示Y1和Y2的投影矩阵,则:
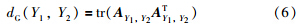
如果在图像库中包含了多个图像样本,可以采用基于GN,d数据的统计方法,利用图像样本综合信息提取特征,提升算法的性能. 由于模糊不变量的维度为(d-N)×N,且d远大于N,通过大量的样本训练可得到每一类图像样本的不同分布. 为能够充分利用图像集合提供的整体信息,更有效地保留样本的判别信息,采用文[12]的方法来进行基于投影核kP的模糊不变量核函数线性判别分析,则:
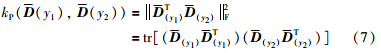
在格拉斯曼流型判别分析的基础上,考虑当数据取样于嵌入在高维空间低维流形的几何空间时,数据点依然保持近邻,局部保持正则化. 设定k在d1×d2的图像y的所有(n1,n2)像素都不变,进行基于黎曼距离dG和低维空间的Euclidean距离的最近邻分类,探针图像的类别可以通过式(8)获取:
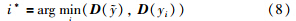
设定模糊核函数k具有空间变化特性,当原空间的非线性信息转化为线性问题处理时,变化空间的维数较高,不同的场景将受到不同的模糊量的影响,比如: 聚焦模糊量、 运动模糊量等. 在这种情况下的图像形成模型可以表示为

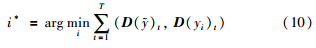
4 实验验证
本节通过实验来验证模糊不变量对噪声的稳健性影响. 将式(1)所示的噪声η分解为

在实验中,由用户控制的唯一参数是模糊核函数的最大尺寸,其决定了字典的列数量. 假设(b1*,b2*)为最大尺寸,则N的值为b1*×b2*,同时,N
分析存在ηq和不同等级的传感器导致的AWGN(additive white Gaussian noise)时,辨识率的变化情况. 利用式(5)计算图像库中的属于一个人的图像在“均匀模糊、 空变模糊、 模糊图像库”条件下的子空间距离. 分别在CMU-PIE(Carnegie Mellon University-Pose Illumination Expression)和YaleB(Yale University Face libraries B)[13, 14]两个图像数据库上进行验证,在实验中,设定图像库图像和探针图像具有相同的光照. 其中PIE数据库的光照图像字库,包含了68个个体的21种不同光照条件的图像,YaleB图像库包含了38个个体的64种不同光照条件的图像.
4.1.1 空间均匀模糊基于4个条件来合成模糊图像: 移动模糊、 聚焦模糊、 Gaussian模糊、 随机模糊. 采用不同的模糊核函数尺寸和不同的光照条件下的图像进行实验. 实验条件分别设定为: 无噪声、 具有量化噪声、 具有脸部变化噪声和AWGN. 对应的信噪比(SNR)分别为50 dB,20 dB,10 dB,5 dB. 先后在清晰图像和模糊图像上分别进行实验,得到12种不同的噪声条件,再通过将探针图像与图像库图像比较来进行识别. 实验中,除了设置12种不同的噪声外,图像库和探针图像包含了68幅图像和38幅图像,分别对应于PIE数据库和YaleB图像库. 实验结果如图 1所示.
这里识别率采用的是人脸识别系统正确识别的测试人脸图像数占总测试人脸图像数的百分比. 识别率越高说明系统的性能越好.
格拉斯曼流型上计算平均和聚类的方法可以分为内在的和外在的,内在的方法完全局限于流形本身,而外在方法可将流形上的点嵌入欧氏空间并使用欧氏度量进行计算. 从图 1可以看出,内部图像和外部图像的误差差异随着噪声的增加而变小. 同时,内部图像的平均误差随着噪声的增加而增加. 由此可见,由于噪声的高频特征,识别率将随着噪声的增加而降低. 即使在没有噪声的条件下,无论清晰图像还是模糊图像,正确匹配的平均误差都不为0. 理论上,个体的模糊图像建立的字典张成的空间与清晰图像是相同的,但是数字化会导致一定的噪声. 对于噪声条件,因为不变量是包含图像所有模糊种类的子空间,模糊图像与清晰图像的统计特性类似,仍能获得变化较为平稳的相对误差.
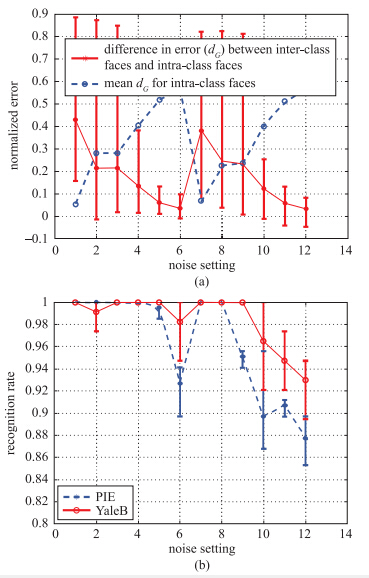 |
| 图 1 噪声对识别的影响Fig. 1 Effect of noise on recognition |
从图像中选取任意大小的图像块,分别采用移动模糊、 聚焦模糊、 Gaussian模糊、 随机模糊4种核函数建立合成的模糊图像,为进行识别,分别选择了尺寸与原图像75%、 50%、 40%重叠的子图像,对于每一种大小的图像块,所建立的字典的大小为N=d1/4×d2/4. 采用空变模糊量的图像块识别结果如图 2所示.
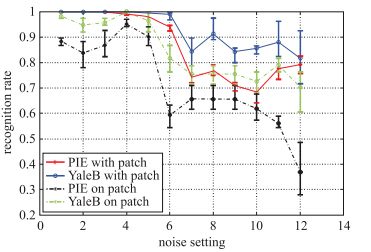 |
| 图 2 噪声对空变模糊量识别结果的影响Fig. 2 Effect of noise on space-variant fuzzy quantity recognition results |
由图 2可知,与均匀模糊量类似,识别率随着噪声的增加而降低. 对于同样的噪声设置,具有空变特性的模糊量较均匀模糊量的识别率低. 这主要是由于两种情况造成的: 1) 模糊核的尺寸通常大于d1/4×d2/4,从而使得字典张成的空间不能包含模糊核; 2) 在模糊核之间存在过渡的区域span(D(·))为模糊不变量.
4.2 存在其它脸部变化的识别性能当脸部表情呈现变化或角度有一定偏转时,与之对应的各类特征的变化即可看作高维人脸表情空间中的一个低维嵌入子流形. 将传统静态人脸表情图像空间的识别拓展到在整个视觉流形格拉斯曼流型上对脸部表情特征进行识别,这样更加丰富了隐含在原始样本中的信息量,使得识别更加准确. 4.2.1 FERET数据库和FRGC数据库的图像识别性能比较
分别对来自FERET数据库的合成模糊图像以及来自FRGC数据库的真实模糊图像的识别性能进行比较[15],实验设置采用与文[16, 21]相同的方式.
1) 采用FERET的图像: fa——图像库,fb——探针图像. 该图像库包含了1 001个个体图像,每个个体对应一幅图像. 同一个人在fa和fb中的人脸图像的表达式和对齐方式的变化很小[17, 18]. 原图像的大小为128×128,将其缩小为64×64,采用大小为5×5、 像素方差σ变化范围为0~8的Gaussian核合成了fb的9幅不同图像[19],同时加入30 dB的高斯白噪声,样本图像识别率如图 3所示. 在合成了不同的核函数[20](例如高斯核函数、 线性移动核函数等)并加入了30 dB的高斯白噪声的条件下,比较本文方法和已有的去模糊方法的识别性能,如表 1所示. 实验数据体现了本文方法在各种不同的模糊核情况下,仍然具有较高的识别率.
 |
| 图 3 采用高斯模糊核进行图像合成情况下各种不同方法的识别性能比较Fig. 3 Performance comparison of recognition with various methods as the image is synthesized by adopting Gaussian blur kernel |
2) 评估在FRGC数据库中的识别性能: 测试图像库包含了608幅图像,这些图像是在非约束光照条件下得到的,其中306幅图像受到了模糊的影响. 除了模糊核光照之外,图像库和探针图像在表情和对齐方式上差异很小. 在表 2中分别比较了有无进行光照补偿的识别情况,可以看出,在光照变化的情况下,识别性能明显提高.
采用UMD数据库,这个数据库包含了17个个体的图像,这些图像既受到不同程度模糊的影响,又受到了不同光照条件、 表情、 对齐方式等影响. 在实验中采用的样本图像如图 4所示,应用最近邻聚类方法来实现人脸图像识别: 一种为没有进行训练,采用格拉斯曼流型上两点之间的距离ηf进行识别,另一种为利用基于核判别分析的训练进行识别,结果如图 5所示. 分析数据可以判断出,即
 |
| 图 4 样本图像Fig. 4 Sample images |
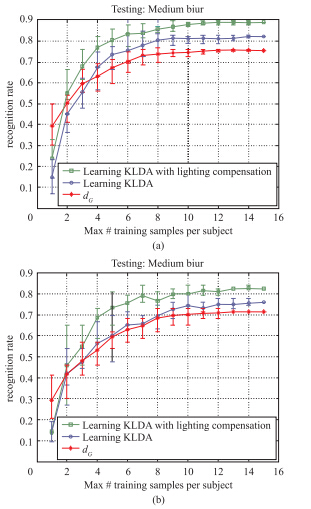 |
| 图 5 对识别性能的影响Fig. 5 Effect on the recognition performance |
使在不完全考虑ηf的情况下,识别率也不会因为采用更多的数据进行训练而得到提高.
5 结论实际应用中,光照、 人脸姿态等外界条件的变化对人脸检测方法的准确度影响很大,例如: 表情的变化容易牵动面部特征点(眼睛、 嘴等)的变化,同一个人的人脸图像往往因为表情的不同而变化很大. 通过研究模糊不变量在其脸部变化下的稳健性,利用图像与完备的正交基卷积得到的子空间能够表示模糊核在一定的假设条件下对模糊量是不变的,基于模糊不变量的直接方法较传统方法具有模糊基任意的特性. 将子空间当作格拉斯曼流型中的一个点,构建出了一种新的模糊不变量,对这些点进行聚类,这是一种基于微分几何学的对于不变量张成的空间的理解. 通过实验分析模糊量在具有同质性和空变性条件下的模糊图像的识别方法,验证了该方法不仅具有良好的模糊不变性,还具有较强的抗噪声能力和较高的图像识别率.
| [1] | Andrews H, Hunt B. Digital image restoration[M]. Upper Saddle River, NJ, USA: Prentice Hall, 1977. |
| [2] | Levin A, Weiss Y, Durand F, et al. Efficient marginal likelihood optimization in blind deconvolution[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ, USA: IEEE, 2011: 2657-2664. |
| [3] | 董光波, 谢桂海, 孙增圻. 基于DSP和小波分析技术的实时噪声消除系统[J]. 计算机工程, 2006, 12(4): 1044-1047. Dong G B, Xie G H, Sun Z Q. Real-time noise cancellation system based on DSP and wavelet[J]. Computer Engineering, 2006, 12(4): 1044-1047. |
| [4] | Tikhonov A N, Arsenin V Y. Solutions of Ill-posed problems[M]//Mathematics of Computation. Washington, USA: V H Winston & Sons, 1997. |
| [5] | 宋家东, 李晓娟, 徐鹏飞, 等. 一种基于模糊2DPLA方法在人脸识别的应用[J]. 小型微型计算机系统, 2011, 32(8): 1647-1651. Song J D, Li X J, Xu P F, et al. Novel method based on fuzzy 2DPLA for application of face recognition[J]. Journal of Chinese Computer System, 2011, 32(8): 1647-1651. |
| [6] | Nishiyama M, Hadid A, Takeshima H, et al. Facial deblur inference using subspace analysis for recognition of blurred faces[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(4): 838-845. |
| [7] | 戴花, 王建平. 模糊支持向量机在人脸识别中的应用[J]. 计算机工程与应用, 2012, 48(6): 158-161. Dai H, Wang J P. Application of face recognition used fuzzy support vector machine[J]. Computer Engineering and Applications, 2012, 48(6): 158-161. |
| [8] | 杜海顺, 李旻, 张帆, 等. 一种模糊双向最大间距准则人脸识别方法[J]. 仪器仪表学报, 2011, 32(5): 1077-1082. Du H S, Li M, Zhang F, et al. Fuzzy bidirectional maximum margin criterion based on face recognition[J]. Chinese Journal of Scientific Instrument, 2011, 32(5): 1077-1082. |
| [9] | 王科俊, 邹国锋. 基于子模式的Gabor特征融合的单样本人脸识别[J]. 模式识别与人工智能, 2013, 26(1): 50-56. Wang K J, Zou G F. A sub-pattern Gabor features fusion method for single sample face recognition[J]. Pattern Recognition and Artificial Intelligence, 2013, 26(1): 50-56. |
| [10] | 顾晓敏, 林锦国, 梅雪. 基于模糊积分分类器融合的人脸识别[J]. 计算机工程, 2010, 36(18): 188-190. Gu X M, Lin J G, Mei X. Face recognition based on classifiers fusion using fuzzy integral [J]. Computer Engineering, 2010, 36(18): 188-190. |
| [11] | 杨海燕, 刘国栋. 基于MB-LBP算子和Multilinear PCA算法的人脸识别[J]. 计算机应用研究, 2012, 29(12): 4733-4735. Yang H Y, Liu G D. Face recognition based on MB-LBP operator and multilinear PCA algorithm[J]. Application Research of Computer, 2012, 29(12): 4733-4735. |
| [12] | Hamm J, Lee D D. Grassmann discriminant analysis: A unifying view on subspace-based learning[C]//Proceedings of the International Conference on Machine Learning. Piscataway, NJ, USA: IEEE, 2008: 376-383. |
| [13] | Sim T, Baker S, Bsat M. The CMU pose, illumination, and expression database[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(12): 1615-1618. |
| [14] | 王守觉, 曲延锋, 李卫军, 等. 基于仿生模式识别与传统模式识别的人脸识别效果比较研究[J]. 电子学报, 2004, 21(7): 586-590. Wang S J, Qu Y F, Li W J, et al. A comparative study on face recognition effect of biomimetic pattern recognition with the traditional pattern recognition[J]. Journal of Electronics, 2004, 21(7): 586-590. |
| [15] | 苏煜, 山世光, 陈熙霖, 等. 基于全局和局部特征集成的人脸识别[J]. 软件学报, 2010, 12(8): 428-432. Su Y, Shan S G, Chen X L, et al. Integration of global and local features of face recognition[J]. Journal of Software, 2010, 12(8): 428-432. |
| [16] | Nishiyama M, Takeshima H, Shotton J, et al. Facial deblur inference to improve recognition of blurred faces[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ, USA: IEEE, 2009: 1115-1122. |
| [17] | 杜干, 朱雯君. 基于局部奇异值分解和模糊决策的人脸识别方法[J]. 中国图象图形学报, 2006, 11(10): 1456-1459. Du G, Zhu W J. Face recognition method and fuzzy decision based on local singular value decomposition[J]. Chinese Journal of Image and Graphics, 2006, 11(10): 1456-1459. |
| [18] | 周丽娟, 肖满生, 文志强, 等. 基于格贴近度的不完全文字图像模糊识别方法[J]. 计算机工程与设计, 2013, 34(12): 4326-4330. Zhou L J, Xiao M S, Wen Z Q, et al. Computer engineering and design of fuzzy recognition method with in complete text image based on lattice degree of nearness[J]. Computer Engineering and Design, 2013, 34(12): 4326-4330. |
| [19] | 史培元, 邓廷权. 颜色的模糊识别方法及其在图像检索中的应用[J]. 计算机工程与应用, 2013(18): 138-141. Shi P Y, Deng T Q. Fuzzy recognition method of color and its application in image retrieval[J]. Computer Engineering and Application, 2013(18): 138-141. |
| [20] | 冯建强, 刘文波, 于盛林. 基于灰度积分投影的人眼定位[J]. 计算机仿真, 2005, 22(4): 75-76. Feng J Q, Liu W B, Yu S L. Eye location based on gray level integration projection[J]. Simulation of Computer, 2005, 22(4): 75-76. |



