1 引言
众所周知,高参数大容量的发电机组过热汽温控制系统性能很难满足实际生产流程控制中对精度的要求. 其原因除了引起过热汽温变化的干扰因素多、 频繁且扰动量大外,还有过热汽温动态特性呈现大迟延、 大惯性和非线性; 更重要的是在保护机组设备的前提下,要求最大限度地提高机组热效率,故过热汽温必须运行在额定温度±5℃的范围内. 显然这些都加大了过热汽温控制的难度. 目前,多数发电机组采用的还是常规的汽温控制系统,如串级汽温控制系统或具有导前汽温微分信号的双回路控制系统. 若常规控制系统中的PID控制器采用固定参数,则只能在特定的运行工况下,才能满足控制性能要求. 显然随着运行工况的变化,常规控制系统很难获得令人满意的控制效果. 近年来提出了许多先进和智能自适应控制器并应用于汽温控制系统,其中模糊推理自适应PID控制器[1, 2, 3]和自适应模糊神经网络控制器[4, 5]等采用多种在线优化控制器参数的方法,对控制性能都有不同程度的改善. 但由于这些方法都是优化控制器的参数,被控过程的大惯性和大时滞特性并没有改善,所以控制性能提高的空间有限. 将预测控制方法应用于过热汽温控制[6],虽然有效地提高了控制性能,但为适应工况变化,需要设计多模型预测控制,这样就必须解决模型切换造成的控制信号振荡问题. 采用各种算法对预测控制器进行优化[7, 8, 9, 10],可使特定工况下的系统跟踪性能得以大幅提高. 无模型自适应预测的汽温控制系统[11]仅用受控过程的I/O数据在线估计系统的伪梯度向量,就能对被控过程进行动态线性化处理得到预估模型. 但要应用于生产中,还需要真正解决实时估计问题. 而将鲁棒H∞控制器应用于过热汽温控制[12, 13, 14],对过程模型不确定的场合是一种有效方法,但克服过程大纯滞后对控制性能的影响不明显.
要想提高大纯滞后过程的控制性能,首先要搞清楚大纯迟延过程难控的本质. 理论和实践表明,当过程控制系统存在大纯迟延环节时,会使系统的闭环特征方程式包含纯迟延因子,这就必然导致系统的稳定性降低,甚至有可能造成系统不稳定. 所以能有效提高大纯迟延过程控制性能的关键是去掉闭环特征方程式中包含的纯迟延因子. 自1957年提出了Smith预估控制后,人们似乎看到了彻底解决该控制问题的希望. 但由于Smith预估器太多依赖于过程精确模型,很长时间并未得到有效应用. 但探索新型Smith预估器设计方法的步伐从未停止,改进结构的Smith预估器也应用而生[15, 16, 17, 18, 19, 20]. 将Smith预估和内模控制相结合的2自由度控制方法[15]能同时提高系统的跟踪和抗干扰能力. 通过自适应辨识器在线调整Smith预估器参数[16, 17],能使Smith预估器的特性与过程特性尽可能一致,以提高控制性能. 在常规串级汽温控制系统中,引入增益自适应Smith预估控制器[18]取得了良好的控制性能. 采用优化策略对Smith预估器进行改进后[19],有效克服了过程参数不确定性给控制性能带来的不良影响; 改进型Smith预估复合模糊过热汽温控制系统[20],采用模糊推理与PID算法并联后构建的复合控制器与改进型的Smith预估器相结合的方案,使得在模型不准确的情况下也能有较好的适应性. 本文通过模糊推理在线调整Smith预估补偿器输出值,提出一种自适应Smith预估补偿的过热汽温控制系统设计方法,以实现在全部运行工况下,对被控过程大纯迟延特性的完全或近似完全补偿. 此方法无需在线辨识过程模型,只要得到过程的静态特性和机组常见工作点的近似数学模型即可. 仿真研究与对比实验表明,自适应Smith预估补偿的过热汽温控制系统的设定值跟踪性能和抗干扰能力都具有明显的优势.
2 自适应Smith预估补偿控制系统设计根据大型发电机组过热汽温被控过程的特点,设计基于自适应Smith预估补偿的过热汽温控制系统工作原理如图 1所示.
 |
| 图 1 自适应Smith预估补偿控制系统的工作原理图Fig. 1 The working principle figure of the adaptive Smith predictive compensation control system |
图 1中,θ10为过热汽温设定值,θ1为过热器出口汽温测量值,θ2为过热器入口汽温测量值,G02(s)为汽温导前区动态特性,G01(s)为汽温惰性区动态特性,G0(s)=G02(s)×G01(s)为减温水扰动下过热汽温的动态特性,GM(s)为指定工作点上Smith预估模型中不包含纯迟延的部分,τM为指定工作点上Smith预估模型中的纯滞后时间,θM为预估模型输出信号,e为预估模型偏差,d为系统干扰信号,K1为Smith预估器模型输出的修正系数,K2为系统开环增益修正系数,fuzzy为模糊控制器.
2.1 Smith预估模型的确定通常发电生产过程经常运行的工况可选作确定Smith预估补偿模型的指定工作点,这是为了实现比较理想的预估补偿效果. 应注意的是,需要采取各种手段,如现场试验、 机理分析和在线辨识等建模方法. 在指定工作点上获得被控过程动态特性的近似数学模型,并将惰性区动态特性采用一阶或二阶惯性环节与纯时滞环节的串联形式表示. 即数学模型近似表达式为
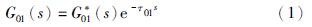
其中,G*01(s)为惰性区动态特性不包括纯滞后的部分,通常为一阶或二阶惯性环节,e-τ01s为惰性区动态特性的纯滞后部分. 根据式(1)可确定图 1中Smith预估模型GM(s)和纯滞后时间τM为
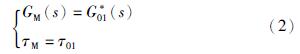
如果在指定工作点上建立的过程数学模型十分精确,那么所确定的Smith预估模型就可以完全补偿惰性区动态特性的纯滞后部分. 但多数情况下只能得到近似模型,即惰性区动态特性的纯滞后部分只能实现近似补偿. 因实际生产过程动态特性具有非线性和时变性,故必须随时在线调整Smith预估模型输出值,才能实现近似完全补偿. 即需满足:
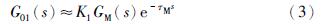
关系成立. 显然,K1在能否实现完全补偿中起着决定性的作用,即实际过程的输出与指定工作点所确定的Smith预估模型输出之间的偏差大小、极性及变化速率是决定K1数值大小的关键因素. 根据以上分析可知,模糊推理是最理想的在线调整K1的方法. 选取2维模糊控制器,其输出值就是预估模型的在线调整系数K1.
如果nT时刻的过程输出为θ1(n),预估模型输出为θM(n),则其预估模型偏差e(n)及其变化率ec(n)可由下式定义:

将模糊控制器输入信号e和ec的模糊子集选择为负大(NB)、负小(NS)、零(ZO)、 正小(PS)和正大(PB),隶属度函数均采用高斯函数. 模糊控制器输出K1的模糊子集选择为很小(VS)、小(S)、中(M)、大(B)和很大(VB),隶属度函数采用三角形函数. 模糊子集的个数可以根据实际过程动态特性的特点适当增加或减少.e、ec和K1的取值范围根据所选择的工作点位置和实际过程动态特性的非线性程度来确定. 若输入e和V数值均为PB,说明实际过程的输出比预估模型输出大很多,而且还在以很快的速率继续增大,此时只有快速增大K1数值才有可能使式(3)的关系成立; 若输入e和ec数值均为NB,说明实际过程输出比预估模型输出小很多,而且还在以很高的速率继续变小,此时只有快速减小K1值才可能使式(3)的关系成立; 若e和V数值均为ZO,说明实际过程输出与预估模型输出完全相等,只有当K1=1时式(3)才成立. 据此分析,设计的模糊推理规则如表 1所示. 同时需要根据工作点位置和实际过程动态特性的非线性程度适当选取量化因子和比例因子的数值,才会使模糊控制器输出的K1值满足式(3)的要求,实现近似完全补偿的目的.
| ec K1 e | NB | NS | ZO | PS | PB |
| NB | VS | VS | VS | S | S |
| NS | VS | VS | S | S | B |
| ZO | VS | S | M | B | VB |
| PS | S | B | B | VB | VB |
| PB | B | B | VB | VB | VB |
随着机组负荷的变化,实际过程的静态增益也在发生变化. 对于图 1所示的自适应Smith预估补偿控制系统,当运行在工作点以外的工况时,反馈信号不是实际过程的输出,所以系统开环增益需要经过系数K2的修正才能与实际过程的静态增益相等. 这样当动态过程结束后,才能使过热汽温θ1回到其设定值θ10,实现消除过热汽温静态偏差的目的. 因此,可根据实际过程随负荷(即蒸汽流量D)变化的静态特性确定适当的函数关系,即:

通过预估补偿后的控制系统,其闭环特征方程式中已经不包含纯迟延环节,所以控制器参数调整范围将会明显扩大,有利于控制性能的提高. 但由于过热汽温对象的导前区特性G02(s)和惰性区特性G01(s)中不包含纯迟延的部分也随机组负荷的变化而不同,显然不能采用固定参数的控制器. 所以需要根据机组蒸汽流量D的数值确定适当大小的PID调节器参数比例带δ,积分时间Ti和微分时间Td,即:

某超临界机组过热汽温随减温水流量变化的近似数学模型已知[1],如表 2所示. 可见该被控对象的动态特性迟延惯性较大且非线性较强. 当负荷由小到大变化时,导前区G02(s)的静态增益将减小,时间常数也将有所减小,惰性区G01(s)的迟延和惯性也减小,但静-态增益变化不会太大.
| 机组负荷 | G02(s) | G01(s) |
|
工况1 (D=179.2 kg/s) | -5.072/(1+28s)2 | 1.048/(1+56.6s)8 |
| 工况2 (D=242.2 kg/s) | -3.067/(1+25s)2 | 1.119/(1+42.1s)7 |
| 工况3 (D=347.9 kg/s) | -1.657/(1+20s)2 | 1.202/(1+27.1s)7 |
| 工况4 (D=527.8 kg/s) | -0.815/(1+18s)2 | 1.276/(1+18.4s)6 |
表 2所示的过热汽温被控对象采用PID-P串级控制系统,得到的主控制器PID、 副控制器P的最佳整定参数,如表 3所示. 选择过热汽温设定值θ10为单位阶跃输入,运行至1 500 s时加入0.2幅值的阶跃干扰d,当采用表 3调节器最佳参数时,得到PID-P串级控制系统的过热汽温θ1的跟踪与抗干扰响应曲线如图 2所示. 可以测得设定值跟踪过程中产生的最大动态偏差为0.08,由于负荷越低对象动态特性的迟延惯性越大,故跟踪过程时间随负荷减少呈现增加趋势. 干扰作用下的最大动态偏差在工况4为最大0.164,跟踪过程持续时间最长为1 150 s. 但当主控制器和副控制器参数采用表 3中工况3负荷时的整定参数不变,得到在各种工况下的过热汽温θ1的响应曲线如图 3所示. 显然工况1和工况2负荷运行时的动态偏差明显增大,甚至会使系统无法继续运行.
| 机组负荷 | 主控制器PID | 副控制器P | ||
| δ | Ti | Td | δ* | |
| 工况1 | 1.18 | 283 | 82 | 1.11 |
| 工况2 | 1.21 | 193 | 60 | 0.15 |
| 工况3 | 1.25 | 127 | 40 | 0.08 |
| 工况4 | 1.37 | 78 | 16 | 0.04 |
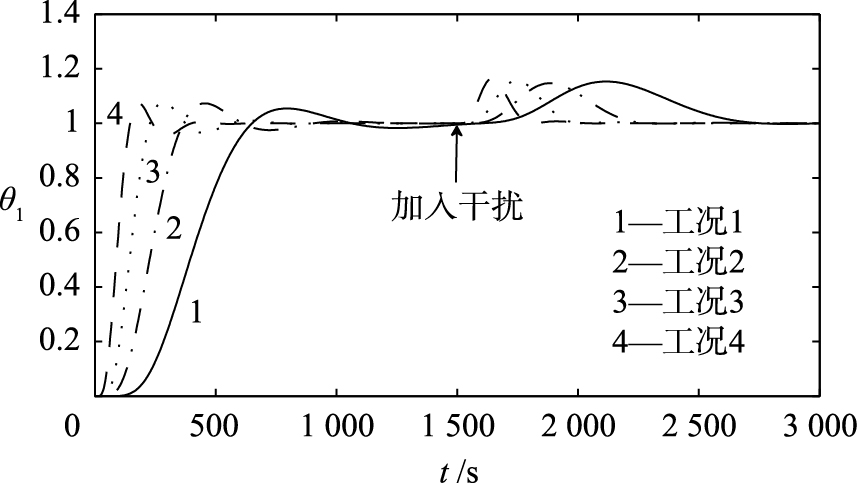 |
| 图 2 在最佳参数下的响应曲线Fig. 2 The response curves with the optimal parameters |
 |
| 图 3 控制器参数固定不变时的响应曲线Fig. 3 The response curves with the fixed parameters of controller |
采用图 1所示的自适应Smith预估补偿控制系统,首先需要确定工作点,设计Smith预估模型. 考虑目前发电机组通常运行在工况3和工况4负荷之间,为了同时兼顾低负荷状态,所以选择工况3作为指定工作点,此时过热汽温惰性区特性为
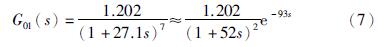
故所设计的Smith预估补偿模型为
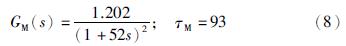
图 1中PID控制器参数和开环增益系数K2的数值随机组负荷变化成单值函数关系,可以采用折线函数近似. 在4种给定负荷下,PID控制器参数和开环增益系数K2的取值如表 4所示.
| 负荷 | PID参数 | 增益 K2 | ||
| δ | Ti | Td | ||
| 工况1 | 2.5 | 200 | 37 | 0.87 |
| 工况2 | 2.0 | 125 | 30 | 0.93 |
| 工况3 | 1.9 | 104 | 28 | 1.00 |
| 工况4 | 1.8 | 78 | 27 | 1.06 |
模糊控制器采用2维结构,偏差信号输入通道的量化因子选择0.4,偏差变化信号输入通道的量化因子选择50,输出信号通道的比例因子选择1. 当过热汽温设定值θ10为单位阶跃信号时,自适应Smith预估补偿控制系统的输出θ1在4种负荷下的响应曲线如图 4所示. Smith预估器模型始终保持不变; 但随着负荷偏离工况75%,实际过程输出和预估模型输出存在偏差,该偏差经模糊推理得到一个相应的修正系数K1,如图 5所示. 该系统就是依靠K1的变化,保证在各种负荷下都能使惰性区动态特性达到近似完全补偿. 由图 4可知,最大动态偏差为0.03,跟踪过程时间最长为1 000 s,可知设定值跟踪性能优于PID-P串级控制系统的最佳工作状态. 在1 500 s时加入幅值为0.2的阶跃信号干扰时,自适应Smith预估补偿控制系统的输出θ1在4种负荷下的抗干扰响应曲线如图 4的曲线后半段所示. 可以测得工况曲线4的动态偏差最大,幅值为0.16,抗干扰性能同样优于PID-P串级控制系统. 由于自适应Smith预估补偿的过热汽温控制系统能够适用于各种工况,且能明显减小对象惰性区特性的大迟延或大惯性,因此其跟踪性能与抗干扰能力自然会比最佳整定参数时的PID-P串级过热汽温控制性能好.
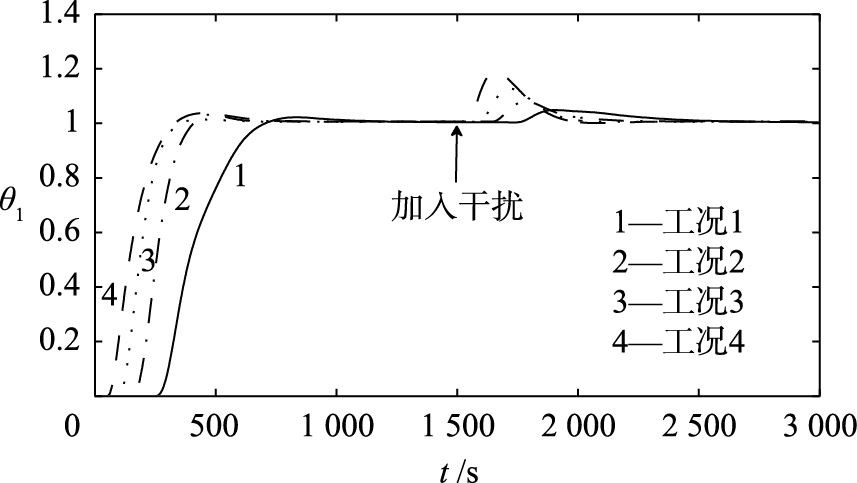 |
| 图 4 自适应Smith预估计补偿控制系统响应曲线Fig. 4 The response curves of adaptive Smith predictor compesation control system |
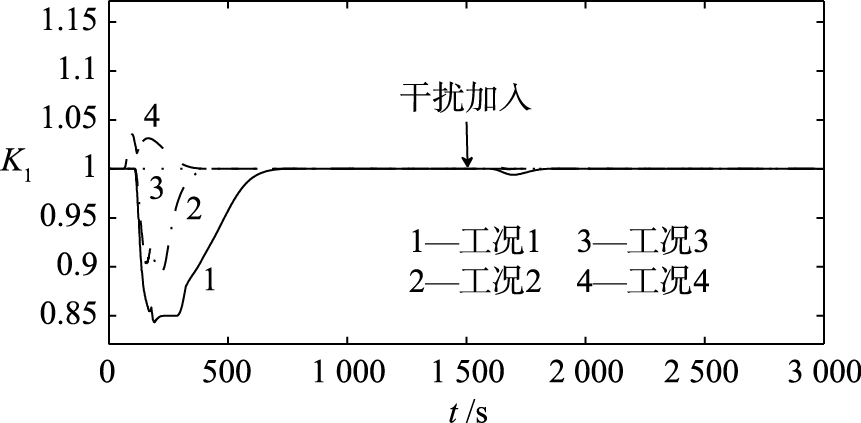 |
| 图 5 自适应Smith预估计补偿模型修正系数K1的变化Fig. 5 The change of the adaptive Smith predictor compesation model correction coefficient K1 |
观察基于分散推理结构的过热汽温模糊控制系统[3]的跟踪响应曲线可知,工况3(即75%负荷)曲线的最大超调量大约在0.1,工况4(即100%负荷)曲线的最大超调量大约0.05. 而自适应Smith预估补偿控制系统的工况3曲线的最大超调量小于0.01,工况4曲线的最大超调量不足0.03.
与采用锅炉过热汽温自适应模糊控制系统[1]相比. 当选择在过热蒸汽流量D=190 kg/s时,对象近似数学模型为
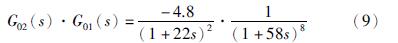
采用本文提出的自适应Smith预估补偿控制系统,其中Smith预估补偿模型保持不变(式(8)). 根据已知蒸汽流量D=190 kg/s,通过式(5)选择PID控制器参数δ=2.34,Ti=176,Td=35; 通过式(4)选择系统开环增益系数K2=0.835. 当过热汽温设定值θ10和干扰信号d均为单位阶跃输入时,其设定值跟踪响应和抗干扰能力比较曲线如图 6所示. 可以测得跟踪曲线上的最大动态偏差小于0.025,跟踪过程持续时间为1 000 s;抗干扰响应曲线的最大动态偏差为0.16,过程持续时间不大于1 330 s. 显然,各种性能均优于过热汽温自适应模糊控制系统.
 |
| 图 6 在蒸汽流量为190 kg/s时的响应曲线Fig. 6 The response curves at steam flow 190 kg/s |
根据改进型Smith预估复合模糊控制系统所给定的汽温对象动态特性:

采用本文提出的自适应Smith预估补偿控制系统,其中Smith预估补偿模型根据文[20]给定的带有纯滞后的1阶惯性特性设置,即纯迟延时间为180 s,惯性时间常数为150 s,放大系数为0.132. 同时可得到PID调节器的参数δ=0.025,Ti=40,Td=3,开环增益系数K2=0.835.当汽温设定值θ10和干扰d均为单位阶跃输入时,如果过程参数不变,则自适应Smith预估补偿控制系统与改进型Smith预估复合模糊控制系统[20]的控制性能一致. 但当过程惰性区时间常数增加20%,即由54.3变为65时,其控制性能对比曲线如图 7所示. 显然本文提出的方案其跟踪和抗干扰性能更好.
 |
| 图 7 时间常数变化20%时的响应曲线Fig. 7 The response curves at changed time constant 20% |
本文提出的自适应Smith预估补偿过热汽温控制系统设计方法简单,控制器参数整定方便. 该系统中Smith预估模型的确定不需要被控过程动态特性的精确表达式,只要依据指定工作点上建立的被控过程近似数学模型即可. 该系统采用模糊推理在线调整Smith预估模型输出值的大小,能够实现在各种运行工况下对过热汽温被控过程大纯迟延特性的完全或近似完全补偿. 因为补偿后的系统闭环特征方程式中不包含纯迟延因子或者明显地减少了纯迟延因子对过程控制性能的不利影响. 所以,该系统不同于单纯优化PID参数的自适应模糊控制系统,它重点优化的是闭环系统动态特性结构,同时根据负荷变化优化PID参数. 仿真研究表明,自适应Smith预估补偿的过热汽温控制系统设定值跟踪性能和抗干扰能力与建立在优化控制器参数层面的自适应控制系统[1, 3]和改进型Smith预估复合模糊控制系统[20]相比均具有一定的优势. 同时,该系统易于分散控制系统组态实现,在实际生产过程中也具有一定的可行性及便利条件.
| [1] | 范永胜, 徐治皋, 陈来九. 基于动态特性机理分析的锅炉过热汽温自适应模糊控制系统研究[J]. 中国电机工程学报, 1997, 17(1):23-28. Fang Y S, Xu Z G, Chen L J. Study of adaptive fuzzy control of boiler superheated steam temperature based on dynamic mechanism analysis[J]. Proceedings of the CSEE, 1997, 17(1):23-28. |
| [2] | 张丽香, 于晋春, 谢克明. 模糊自适应导前微分方式的过热汽温控制系统[J]. 动力工程, 2002, 22(4):1893-1896. Zhang L X, Yu J C, Xie K M. The boiler steam temperature fuzzy-adaptation guidance differential control system[J]. Power Engineering, 2002, 22(4):1893-1896. |
| [3] | 刘翠花, 陈红, 王广军. 基于分散推理结构的过热汽温模糊控制及仿真[J]. 系统仿真学报, 2011, 23(7):1437-1440. Liu C H, Chen H, Wang G J. Fuzzy control and simulation based on distributed inferential structure for superheated temperature[J]. Journal of System Simulation, 2011, 23(7):1437-1440. |
| [4] | 韩璞, 孙海蓉, 周黎辉. 自适应神经元PID控制器在过热汽温控制中的应用[J]. 华北电力大学学报, 2005, 32(5):62-65. Han P, Sun H R, Zhou L H. Application of self adaptive neuron PID controller in superheated steam temperature control[J]. Journal of North China Electric Power University, 2005, 32(5):62-65. |
| [5] | 牛培峰, 张密哲, 陈贵林, 等. 自适应模糊神经网络控制在锅炉过热汽温控制中的应用[J]. 动力工程学报, 2011, 31(2):115-119. Niu P F, Zhang M Z, Chen G L, et al. Application of adaptive fuzzy-neural control for superheated steam temperature of boilers[J]. Journal of Chinese Society of Power Engineering, 2011, 31(2):115-119. |
| [6] | 袁立川, 丁艳军, 李东海. 过热汽温多模型预测控制的现场应用[J]. 清华大学学报:自然科学版, 2010, 50(8):1258-1262. Yuan L C, Ding Y J, Li D H. Field application of multiple model predictive control for superheat temperature in boilers[J]. Journal of Tsinghua University:Science and Technology, 2010, 50(8):1258-1262. |
| [7] | 肖本贤, 王晓伟, 朱志国, 等. 基于改进PSO算法的过热汽温神经网络预测控制[J]. 控制理论与应用, 2008, 25(3):569-573. Xiao B X, Wang X W, Zhu Z G, et al. Neural network predictive control for superheated steam temperature based on modified particle swarm optimization[J]. Control Theory & Applications, 2008, 25(3):569-573. |
| [8] | Liu X J, Chan C W. Neuro-fuzzy generalized predictive control of boiler steam temperature[J]. IEEE Transactions on Energy Conversion, 2006, 21(4):900-908. |
| [9] | 许鸣珠, 刘贺平, 李晓理, 等. 过热汽温的稳定自适应预测函数控制[J]. 中国电机工程学报, 2007, 27(11):88-92. Xu M Z, Liu H P, Li X L, et al. Steady adaptive predictive functional control of main steam temperature[J]. Proceedings of the CSEE, 2007, 27(11):88-92. |
| [10] | 冯建苗, 李少远. 电厂过热汽温串级系统的约束预测控制[J]. 上海交通大学学报, 2011, 45(10):1504-1508, 1515. Feng J M, Li S Y. Cascade constrained predictive control for power plant superheated steam temperature system[J]. Journal of Shanghai Jiaotong University, 2011, 45(10):1504-1508, 1515. |
| [11] | 冯玉昌, 史冬琳. 无模型自适应预测控制在过热汽温控制中的应用[J]. 热能动力工程, 2011, 26(4):428-431. Feng Y C, Shi D L. Application of the model-free self-adaptive prediction control in superheated steam temperature control[J]. Journal of Engineering for Thermal Energy and Power, 2011, 26(4):428-431. |
| [12] | Menkina M. Possibility of robust temperature control of superheated steam of the through-flow boiler[C]// Proceedings of 13th International Carpathian Control Conference.Piscataway, NJ, USA:IEEE, 2012:474-479. |
| [13] | 张长青, 杨锋, 薛建中, 等. 锅炉汽温控制H∞性能状态观测器的设计[J]. 中国电机工程学报, 2006, 26(14):109-113. Zhang C Q, Yang F, Xue J Z, et al. The design of the H∞performance state observer for the boiler steam temperature control[J]. Proceedings of the CSEE, 2006, 26(14):109-113. |
| [14] | 高云霞, 田沛, 李沁, 等. 基于H∞混合灵敏度的主汽温控制系统的研究[J]. 华北电力大学学报, 2006, 33(1):76-79. Gao Y X, Tian P, Li Q, et al. Research on main steam temperature control system based on H∞ mixed sensitivity[J]. Journal of North China Electric Power University, 2006, 33(1):76-79. |
| [15] | 张井岗, 刘志远, 陈志梅, 等. 时滞系统的二自由度控制[J]. 信息与控制, 2002, 31(4):325-328. Zhang J G, Liu Z Y, Chen Z M, et al. Two-degree-of-freedom control for time-delay system[J]. Information and Control, 2002, 31(4):325-328. |
| [16] | 刘川来, 刘鹏飞, 宁通. 纯滞后串级控制系统的新型控制算法[J]. 信息与控制, 2009, 38(2):245-248. Liu C L, Yang P F, Ning T. A new control method for the cascade control system with pure time-delay[J]. Information and Control, 2009, 38(2):245-248. |
| [17] | Zhang L X. The study and application of integrated control strategy[C]// Proceedings of the 2012 IEEE International Computer Science and Automation Engineering (CSAE).Piscataway, NJ, USA:IEEE, 2012:1-5. |
| [18] | 罗嘉, 李锋, 张红福, 等. 过热汽温增益自适应Smith预估控制[J]. 电力系统及其自动化学报, 2010, 22(1):156-160. Luo J, Li F, Zhang H F, et al. Gain adaptive Smith prediction control of superheated steam temperature[J]. Proceedings of the CSU-EPSA, 2010, 22(1):156-160. |
| [19] | 马增辉, 刘长良, 开平安. 基于扰动补偿的大滞后系统的控制[J]. 信息与控制, 2013, 42(5):570-576. Ma Z H, Liu C L, Kai P A. Control of dead-time systems based on disturbance compensation[J]. Information and Control, 2013, 42(5):570-576. |
| [20] | 孙宇贞. 过热汽温的改进型Smith预估复合模糊控制[J]. 上海电力学院学报, 2014, 30(3):265-268. Sun Y Z. Improved Smith predictor and composited fuzzy control of superheater steam temperature[J]. Journal of Shanghai University of Electric Power, 2014, 30(3):265-268. |



