1引言
软测量技术是一种实现在化工过程中难测变量在线测量的有效办法，为实现过程的监测、控制与优化提供了必要的基础，其中建模方法是软测量技术的核心研究内容[1].常规软测量建模方法主要有机理建模与数据驱动建模，机理建模方法具有工程背景清晰、可解释性强等优点，但存在可移植性差和模型结构复杂等问题，特别是对于机理复杂或机理知识匮乏的场合，难以建立比较完善的机理模型[2].因此，以过程数据为基础的数据驱动建模方法在软测量中得到了广泛研究与应用[3,5].数据驱动建模方法以过程数据为基础，仅需较少的过程机理知识，具有较强的灵活性和通用性.但存在可解释性较差和易受样本数据影响等问题，且各类方法自身均存在不足，易影响软测量模型的预测精度和稳定性.
针对上述数据驱动建模方法存在的不足，国内外研究者提出了一些改进方法，其中数据驱动融合建模方法是一种较为有效的方法[6].数据驱动融合建模方法的基本思路是：首先通过对样本数据的处理产生若干训练集；然后针对各训练集建立数据驱动子模型；最后采用融合算法实现各子模型的有效融合.根据训练集产生方式的不同，数据驱动融合建模方法主要分为集成学习[7,9]和聚类分析[10,12].
针对单一神经网络存在预测能力不足的问题，利用数据驱动融合建模方法的基本思想，提出一种核主元分析(KPCA)-bagging集成神经网络软测量建模方法.首先，为了消除辅助变量之间的冗余性及降低整体模型的复杂性和提高建模效率，采用KPCA对辅助变量进行特征提取，实现数据非线性降维；然后将bagging集成学习算法与BP神经网络相结合，训练出多个存在差异性的BP神经网络子模型，采用网格搜索法优化确定BP神经网络结构与集成模型规模；最后针对各子模型之间存在的复共线性问题，采用岭回归方法实现子模型输出融合，并采用聚丙烯熔融指数的工业数据对该建模方法进行性能验证.仿真结果表明，与BP神经网络模型和KPCA-BP神经网络模型相比，KPCA-bagging集成神经网络模型具有更好的预测精度和泛化能力.
2 基于KPCA的数据降维由于许多化工过程的变量间存在强非线性相关，因此可采用核主元分析方法进行数据非线性降维，其基本原理为：首先引入核函数将样本数据映射到高维特征空间从而消除变量间的非线性关系，然后通过主元分析提取反映样本特征的主要信息[13,15].
假设样本数据X=｛x1，x2，…，xm｝，其中xk∈RN(k=1，…，m)，m为样本总数.设φ为非线性映射，对应的空间记作F，其中的样本记为φ(xk).
当
时，F空间的样本协方差矩阵为
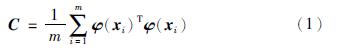
则矩阵C的特征值λ与特征向量V可表示为
将式(2)两边同乘以φ(xk)(k=1，…，m)可得
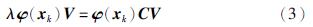
其中，特征值(非零)对应的特征向量V可表示成
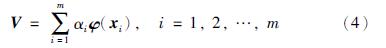
引入核函数Kij：
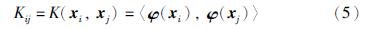
则求协方差矩阵C的特征值与特征向量可转化为求核函数矩阵K的特征值与特征向量：
将特征值降序排列，单位正交化对应的特征向量，并以主元贡献率为依据提取主分量α′，最终得到核矩阵在部分特征向量上的投影，即主元.
上述推导是基于，而实际情况不一定成立，式(6)中的核矩阵K需要进行修正：
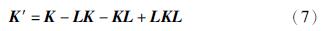
式中，L是系数为1/m的m×m阶单位矩阵.
采用KPCA实现数据非线性降维的具体实施步骤如下：
(1)选择合适的核函数，设置相应合适的核参数，并根据式(5)计算得到核矩阵K；
(2)根据式(7)对核矩阵K进行修正得到K′；
(3)根据式(6)计算得到核矩阵K′的特征值与特征向量，对特征值进行降序排列，并得到对应的特征向量；
(4)单位正交化特征向量得到α1，α2，…，αn；
(5)设置合适的累积贡献率阈值，根据特征值提取相应的主分量α1，α2，…，αt；
(6) 计算核矩阵K′在主分量上的投影，X′=K′α′，得到降维后的结果.
3 bagging集成神经网络神经网络具有较强的非线性拟合能力，且无需过多的先验知识，在缺乏机理知识的化工过程软测量建模中具有较大优势.但神经网络的网络结构难以最优化且过分依赖学习样本，从而导致泛化能力不强等问题.对此一些研究者开展了改进研究，其中通过集成多个神经网络以改善整体模型性能的研究思路获得了较多关注[16,17].
bagging集成学习算法的基本原理为：给定一个弱学习机和一个训练集，首先从训练集中进行放回式随机抽取训练样本，反复进行c次，产生c个训练集；然后分别对各个训练集训练弱学习机，得到c个子模型；最后集成这些子模型得到最终预测模型[18,19].因此，将bagging集成学习算法与BP神经网络相结合，提出一种bagging集成神经网络建模方法.
在建立bagging集成神经网络模型过程中，如何确定子模型的权重系数对整体模型的预测性能影响较大.目前常采用线性加权方法，但由于各个子模型均是对同一映射关系建模，各个子模型输出之间存在复共线性问题，若采用线性加权方法计算权重系数，将导致回归信息矩阵为奇异或近似于奇异，使得估计值不稳定.因此可从减少回归系数均方误差的角度出发，采用岭回归方法改进最小二乘回归[20].
bagging集成神经网络的预测输出向量ybagging为
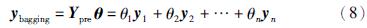
式中，Ypre为n个神经网络的预测矩阵，θ为组合权重系数向量，权重系数θi满足：
当以最小化模型预测误差平方和作为最优时，可计算得到组合权重系数向量θ.按此思路可将权重系数向量的求解问题转化为条件极值问题，即在约束条件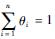
之下，通过最小化
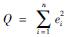求参数θj的估计值.为此可建立条件极值问题的拉格朗日函数：
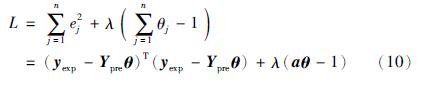
式中，yexp表示模型的期望输出向量，a表示分量全为1的n维行向量.
采用拉格朗日乘子法可求解得到权重系数向量θ的具体计算公式为
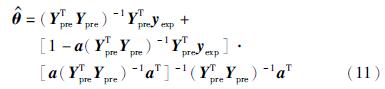
由于各个子模型输出之间存在复共线性问题，导致回归信息矩阵YTpreYpre为奇异或接近于奇异，采用岭回归方法改进式(11)，权重系数向量估计值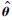
的改进计算公式为
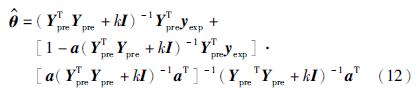
式中，k是正常数，可采用岭迹法得到.
建立bagging集成神经网络模型的具体步骤如下：
(1)建立样本数据集X′，设置样本提取率；
(2)经过c次循环，对样本数据集X′进行反复随机抽样，得到c个子集｛X′1，X′2，…，X′c｝；
(3)训练各个子集建立c个BP神经网络模型｛NN1，NN2，…，NNc｝；
(4)根据各BP神经网络模型的输出｛y1，y2，…，yc｝与期望输出yexp，采用式(12)计算得到各模型的权重系数，实现子模型输出融合，建立bagging集成神经网络模型.
4 KPCA-bagging集成神经网络建模算法将KPCA与bagging集成神经网络相结合，提出一种KPCA-bagging集成神经网络建模方法，其模型结构如图 1所示.
 |
| 图 1 KPCA-bagging集成神经网络模型结构Fig. 1 The structure of KPCA-bagging ensemble neural network model |
由于BP神经网络的具体结构与集成模型规模对整体模型性能影响较大，为了避免BP神经网络结构参数与集成模型规模选择的主观性，采用网格搜索法优化选择隐含层单元个数与集成模型规模.
将KPCA-bagging集成神经网络建模方法应用于化工过程软测量的具体实施步骤如下：
(1)根据化工对象的特点和软测量任务要求，确定辅助变量与主导变量，采集样本数据并进行预处理，构建样本数据集；
(2)根据KPCA的具体实施步骤对训练集进行非线性降维，提取非线性主元作为模型输入；
(3)设置单隐含层单元个数i与集成模型规模c的取值范围分别为[t-2，t+2]和[c1，c2].其中，t表示输入变量个数，故网络结构为t-i-1；c1和c2分别表示集成模型规模的下限和上限.根据bagging集成神经网络模型的具体步骤，针对网格节点中的参数值分别建立bagging集成神经网络模型；
(4)利用所有训练集对所有bagging集成神经网络模型进行性能测试，选择平均相对误差(MRE)作为模型性能的评价指标，优化筛选得到bagging集成神经网络模型，并获得相应的隐含层单元个数i与集成模型规模c；
(5)将KPCA-bagging集成神经网络模型应用于化工过程软测量研究中，实现重要质量指标的在线实时估计.
5 仿真实验熔融指数是聚丙烯产品的重要质量指标，其产品牌号一般通过熔融指数来划分.在聚丙烯生产过程中，熔融指数由离线分析得到，存在较大测量滞后，使熔融指数离线分析值难以用于聚丙烯在线质量控制，因此需要建立有效的聚丙烯熔融指数在线预测模型[21].以某企业Spheripol工艺聚丙烯生产装置为应用对象，采用KPCA-bagging集成神经网络建模方法建立聚丙烯熔融指数软测量模型，以验证该建模方法的有效性.
5.1聚丙烯熔融指数软测量模型根据丙烯聚合动力学及Spheripol双环管工艺，选择软测量模型的辅助变量为：催化剂体系流率(Fcat)、双环管氢气浓度([H2]1、[H2]2)、双环管丙烯单体流率(FM，1、FM，2)、双环管夹套冷却水温度(Tcw，1、Tcw，2)、反应温度(T)，主导变量为熔融指数.辅助变量数据由聚丙烯生产企业的数据服务器实时采集得到，主导变量数据由现场采集的聚丙烯样品离线分析得到.
对原始数据进行数据预处理，采用滤波方法消除数据中的随机误差，利用莱以特准则剔除异常数据，并进行数据标准化处理.经数据预处理后，得到3个聚丙烯牌号共165组数据，其中各牌号的数据均为55组.在各牌号样本数据中，前35组训练样本数据用于建立模型，后20组测试样本数据用于模型性能测试.
采用KPCA对各牌号的训练样本数据进行非线性降维，首先需要确定合适的核函数及其核参数.将KPCA与BP神经网络相结合，对高斯核函数、多项式核函数等常用核函数进行测试，根据测试结果选择高斯核函数作为核函数.考察高斯核函数的核宽度变化对降维效果的影响，发现核宽度较小时降维效果不明显，逐渐增大后效果逐渐好转，超过某一个范围后则效果基本不变，最终确定核宽度σ=15.若选择过小的累积贡献率将会损失大量有效信息，而选择过大则会导致降维效果不明显，因此最终确定累积贡献率p=85％.以牌号Ⅰ为例，KPCA的非线性降维结果如表 1所示，根据累积贡献率选择4个主元.同理，牌号Ⅱ、Ⅲ的主元个数分别为6和5.
| 第i个主元 | 特征值 | 贡献率 | 累积贡献率 | 1 | 0.338 | 0.413 | 0.413 | 2 | 0.197 | 0.241 | 0.654 | 3 | 0.130 | 0.159 | 0.813 | 4 | 0.082 | 0.100 | 0.913 |
将非线性降维处理后的主元用于建立bagging集成神经网络模型，各BP神经网络子模型均为3层结构，隐含层单元函数为tansig型函数，输出层单元函数为purelin型函数，训练的终止误差为1×10-3，训练算法为Levenberg-Marquardt算法，采用网格搜索法确定隐含层单元个数与集成模型规模.牌号Ⅰ、Ⅱ、Ⅲ对应的隐含层单元个数取值范围分别为[2, 6]、[4, 8]、[3, 7]，集成模型规模的取值范围均为[2, 10]，样本提取率为80％.以牌号I为例，不同隐含层单元个数和集成模型规模下的KPCA-bagging集成神经网络模型性能测试结果如图 2所示.根据图 2可知，最优的隐含层单元个数为5个，集成模型规模为4个.
 |
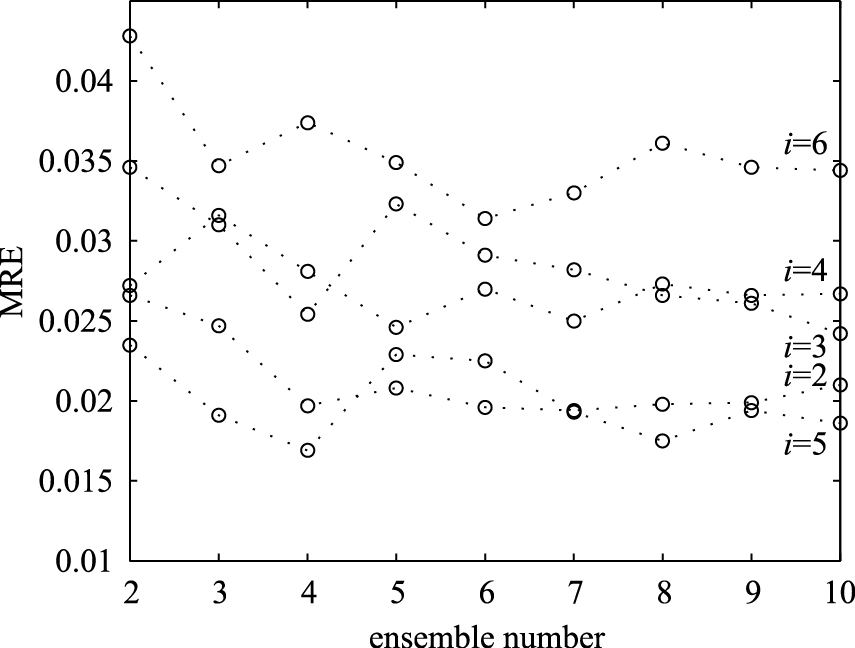| 图 2 模型性能测试结果(牌号Ⅰ)Fig. 2 hetestresultsofthemodelperformance(gradeⅠ) |
采用网格搜索法得到3个牌号的BP神经网络结构与集成模型规模，具体结果如表 2所示.
| 牌号 | 网络结构 | 集成模型规模 | Ⅰ | 4-5-1 | 4 | Ⅱ | 6-5-1 | 5 | Ⅲ | 5-7-1 | 2 |
采用岭回归方法计算bagging集成神经网络模型的权重参数，各牌号整体软测量模型的模型输出具体计算公式如下：
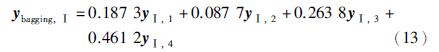
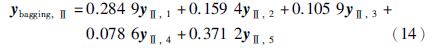
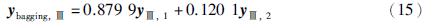
其中，式(13)～(15)右边的yi，j表示牌号i中第j个BP神经网络模型的预测输出.
5.2预测结果比较为了验证KPCA-bagging集成神经网络建模方法的有效性，针对聚丙烯3个牌号，分别建立了3种聚丙烯熔融指数软测量模型：BP神经网络模型(A)、KPCA-BP神经网络模型(B)和KPCA-bagging集成神经网络模型(C)，并比较3种模型的预测效果.模型A在3个牌号下的网络结构均为8-7-1；模型B在3个牌号下的主元个数分别为4、6、5，网络结构分别为4-5-1、6-5-1、5-7-1；模型A、B的其它参数设置内容与模型C相同.针对聚丙烯3个牌号，3种软测量模型预测值与离线分析值的比较结果如图 3～5所示.
 |
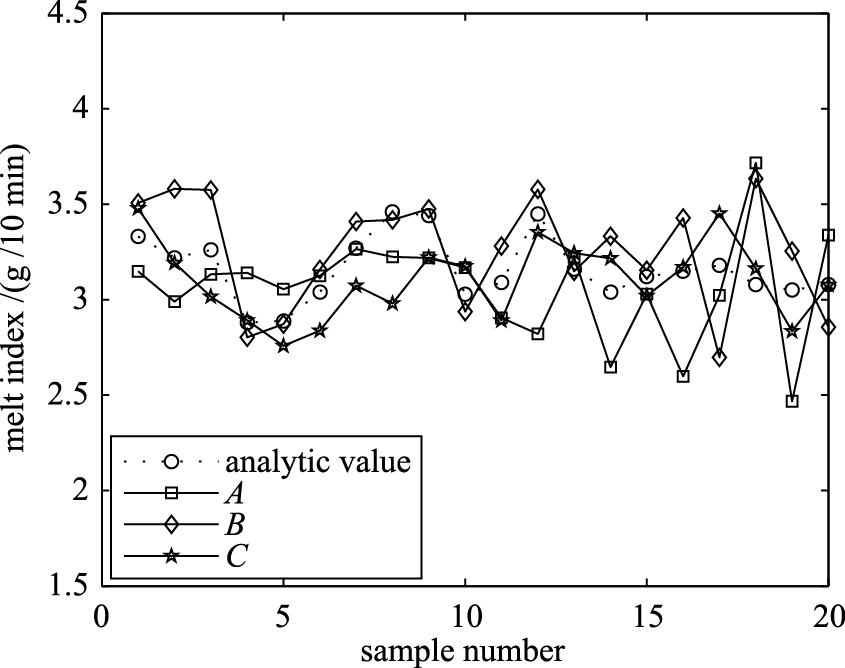| 图 3 熔融指数预测结果比较(牌号Ⅰ)Fig. 3 The comparison of melt index prediction results(gradeⅠ) |
 |
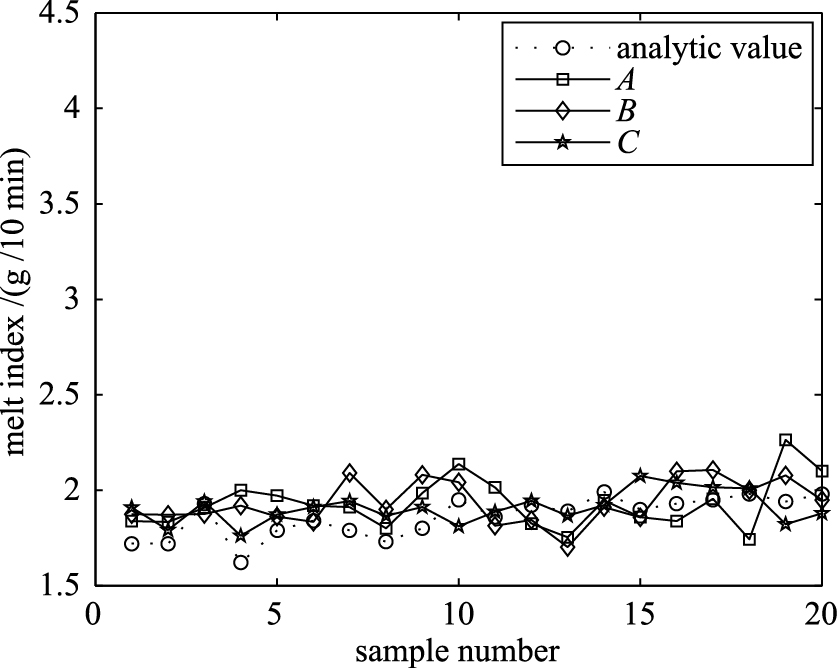| 图 4 熔融指数预测结果比较(牌号Ⅱ)Fig. 4 The comparison of melt index prediction results(gradeⅡ) |
 |
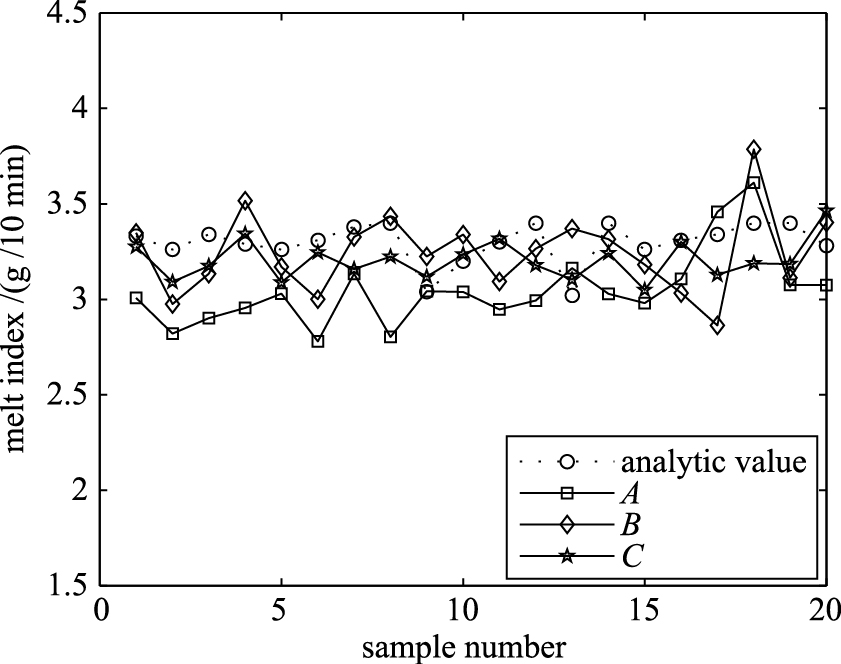| 图 5 熔融指数预测结果比较(牌号Ⅲ)Fig. 5 The comparison of melt index prediction results(gradeⅢ) |
为了定量比较3种模型的预测性能，采用σMRE(平均相对误差)、σMAE(平均绝对误差)和σRMSE(相对均方差误差)作为模型预测性能指标.3个牌号的3种模型预测性能指标数值如表 3～5所示，其中各预测性能指标的具体计算公式如下：
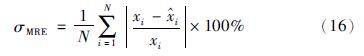
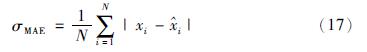
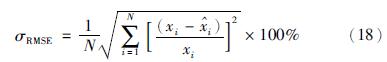
式中，xi表示模型预测值，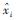
i表示离线分析值，N表示样本数目.
| 模型 | σMRE/％ | σMAE/(g/10min) | σRMSE/％ | A | 8.23 | 0.259 | 2.27 | B | 5.35 | 0.169 | 1.47 | C | 3.86 | 0.123 | 0.99 |
| Model | σMRE/％ | σMAE/(g/10min) | σRMSE/％ | A | 7.39 | 0.135 | 2.04 | B | 6.95 | 0.126 | 1.94 | C | 4.65 | 0.085 | 1.23 |
| Model | σMRE/％ | σMAE/(g/10min) | σRMSE/％ | A | 8.91 | 0.296 | 2.20 | B | 5.13 | 0.168 | 1.33 | C | 3.54 | 0.117 | 0.90 |
由图 3～图 5可知，3个牌号的聚丙烯熔融指数预测结果均表明，与BP神经网络模型、KPCA-BP神经网络模型相比，KPCA-bagging集成神经网络模型具有更好的预测能力，能更好地跟踪熔融指数的变化.由表 3～表 5可知，与BP神经网络模型相比，KPCA-bagging集成神经网络模型的预测性能指标数值均降低了50％左右；与KPCA-BP神经网络模型相比，KPCA-bagging集成神经网络模型也具有明显优势.聚丙烯熔融指数仿真研究表明，KPCA-bagging集成神经网络模型具有较好的预测精度和泛化能力，验证了该建模方法的有效性.
6结论本文提出了一种KPCA-bagging集成神经网络建模方法，该方法通过将非线性数据降维方法、集成建模方法以及岭回归方法相结合，克服了常规神经网络建模方法存在的不足，并对重要模型参数进行了优化，实现了复杂化工过程质量建模.聚丙烯熔融指数软测量仿真结果表明，与BP神经网络模型和KPCA-BP神经网络模型相比，采用KPCA-bagging集成神经网络建模方法建立的聚丙烯熔融指数软测量模型具有更佳的预测性能.
| [1] | 曹鹏飞, 罗雄麟. 化工过程软测量建模方法研究进展[J]. 化工学报, 2013, 64(3):788-800. Cao P F, Luo X L. Modeling of soft sensor for chemical process[J]. CIESC Journal, 2013, 64(3):788-800. |
| [2] | von Stosch M, Oliveira R, Peres J, et al. Hybrid semi-parametric modeling in process systems engineering:Past, present and future[J]. Computers and Chemical Engineering, 2014, 60:86-101. |
| [3] | Gunther J C, Conner J S, Seborg D E. Process monitoring and quality variable prediction utilizing PLS in industrial fed-batch cell culture[J]. Journal of Process Control, 2009, 19(5):914-921. |
| [4] | Kashani M N, Aminian J, Shahhosseini S, et al. Dynamic crude oil fouling prediction in industrial preheaters using optimized ANN based moving window technique[J]. Chemical Engineering Research and Design, 2012, 90(7):938-949. |
| [5] | Wang J L, Feng X Y, Yu T. A geometric approach to support vector regression and its application to fermentation process fast modeling[J]. Chinese Journal of Chemical Engineering, 2012, 20(4):715-722. |
| [6] | Bates J M, Granger C W J. The combination of forecasts[J]. Operations Research Quarterly, 1969, 20(4):451-468. |
| [7] | Ge Z Q, Song Z H. Bagging support vector data description model for batch process monitoring[J]. Journal of Process Control, 2013, 23(8):1090-1096. |
| [8] | 田慧欣, 王安娜. 基于增量学习思想的改进AdaBoost建模方法[J]. 控制与决策, 2012, 27(9):1433-1436. Tian H X, Wang A N. Improved AdaBoost modeling method based on incremental learning[J]. Control and Decision, 2012, 27(9):1433-1436. |
| [9] | Zhang S N, Wang F L, He D K, et al. Real-time product quality control for batch processes based on stacked least-squares support vector regression models[J]. Computers and Chemical Engineering, 2012, 36:217-226. |
| [10] | 丛秋梅, 苑明哲, 王宏, 等. 基于元学习的污水水质集成软测量模型[J]. 信息与控制, 2014, 43(2):248-252. Cong Q M, Yuan M Z, Wang H, et al. Soft-sensor of water quality based on integrated ELM with meta-learning[J]. Information and Control, 2014, 43(2):248-252. |
| [11] | Li X L, Su H Y, Chu J. Multiple model soft sensor based on affinity propagation, Gaussian process and Bayesian committee machine[J]. Chinese Journal of Chemical Engineering, 2009, 17(1):95-99. |
| [12] | 张宇献, 李松, 董晓. 基于特征聚类数据划分的多神经网络模型[J]. 信息与控制, 2013, 42(6):693-699. Zhang Y X, Li S, Dong X. Multiple neural network model based on data partition using feature clustering[J]. Information and Control, 2013, 42(6):693-699. |
| [13] | 唐春霞, 阳春华, 桂卫华, 等. 基于KPCA-LSSWM的硅锰合金熔炼过程炉渣碱度预测研究[J]. 仪器仪表学报, 2010, 31(3):689-693. Tang C X, Yang C H, Gui W H, et al. KPCA and LSSVM model-based slag basicity Prediction for silicomanganese smelting process[J]. Chinese Journal of Scientific Instrument, 2010, 31(3):689-693. |
| [14] | 王强, 田学民. 基于KPCA-LSSVM的软测量建模方法[J]. 化工学报, 2011, 62(10):2813-2817. Wang Q, Tian X M. Soft sensing based on KPCA and LSSVM[J]. CIESC Journal, 2011, 62(10):2813-2817. |
| [15] | 李海波, 柴天佑, 岳恒. 浮选工艺指标KPCA-ELM软测量模型及应用[J]. 化工学报, 2012, 63(9):2892-2898. Li H B, Chai T Y, Yue H. Soft sensor of technical indices based on KPCA-ELM and application for flotation process[J]. CIESC Journal, 2012, 63(9):2892-2898. |
| [16] | Sridhar D, Seagrave R, Bartlett E. Process modeling using stacked neural networks[J]. AIChE Journal, 1996, 42(9):2529-2539. |
| [17] | Zhang J. Inferential estimation of polymer quality using bootstrap aggregated neural networks[J]. Neural Networks, 1999, 12(6):927-938. |
| [18] | Chen T, Ren J H. Bagging for Gaussian process regression[J]. Neurocomputing, 2009, 72(7/8/9):1605-1610. |
| [19] | 田慧欣, 贾玉凤. 基于集成多支持向量回归融合的上浆率在线软测量方法[J]. 纺织学报, 2014, 35(1):62-66. Tian H X, Jia Y F. Online soft measurement of sizing percentage based on intergrated multiple SVR fusion by Bagging[J]. Journal of Textile Research, 2014, 35(1):62-66. |
| [20] | 夏陆岳, 俞立. 基于SNNs-RR的聚丙烯熔融指数软测量[J]. 化工学报, 2008, 59(7):1631-1634. Xia L Y, Yu L. Melt index prediction of polypropylene based on SNNs-RR[J]. CIESC Journal, 2008, 59(7):1631-1634. |
| [21] | 李文义, 陈果, 王靖岱, 等. Spheripol工艺丙烯聚合质量模型[J]. 高校化学工程学报, 2008, 22(1):100-105. Li W Y, Chen G, Wang J D, et al. Mathematical modeling of polypropylene quality for Spheripol process[J]. Journal of Chemical Engineering of Chinese Universities, 2008, 22(1):100-105. |