2. 数字社区教育部工程研究中心, 北京 100124;
3. 计算智能与智能系统北京市重点实验室, 北京 100124
2. Engineering Research Center of Digital Community, Ministry of Education, Beijing 100124, China;
3. Beijing Key Laboratory of Computational Intelligence and Intelligent System, Beijing 100124, China
1 引言
PID控制器以其算法简单和鲁棒性强[1, 2]的优点被广泛应用于工业、航空等领域的过程控制系统中[3, 4]. 其参数整定情况对控制性能有着直接影响,吸引了众多学者在控制精度[5]、实时性[6]、 学习能力[7]和自适应性[3]等方面做了大量的研究和有益的探索. 然而,由于被控过程往往具有强非线性、强耦合性、 时变性和大惯性等特点,PID参数的整定方法还存在繁琐、不易理解和学习能力不足等缺陷,使得性能指标难以满足要求. 因此,还需进一步改进PID参数的整定方法.
从整定PID参数的发展来看,经验公式法出现最早,比如经典的Z-N法[8]和Cohen-Coon法[9]是通过获取被控对象的模型参数或响应特性来求出PID参数.虽然操作简单,但调节质量一般,应用时还需不断修正参数. 之后出现的指标函数优化法考虑被控对象的综合性能,其中较典型的是时间加权平方误差积分(integral squared time-weighted errors,ISTE)最优整定法[10],虽然该方法在理论上具备可行性,并有参数的计算公式,但调节时间、 超调量等单个指标间还缺乏明显的对应关系,实际应用时不易掌握. 可见,经验公式法的整定效果依赖于被控对象的模型参数是否准确,而实际对象的准确模型往往难以建立. 为了避免这个问题,工程整定法应运而生,主要是通过实验获得被控对象的阶跃响应,或者对象本身的特性曲线,再采用衰减曲线法、 临界比例度法或响应曲线法去整定PID参数.但也存在一些问题,如响应曲线的参数读取存在误差、 临界稳定点难以确定等,因此该方法的适用范围仍然有限. 于是,自整定技术得以发展,如采用遗传算法[11]对PID参数进行智能搜索和自适应调整; 利用专家系统和模糊决策等智能推理技术实现PID参数的自适应整定[12, 13].以上方法不依赖于对象的数学模型、 勿需获取精确的响应曲线,因此取得了一定成果.但这些自整定方法自身也存在许多不足,如遗传算法易限入局部最优、 自动调整的时间复杂度高和整定知识的获取比较困难等,给控制系统的实时性、适应性和可靠性等性能带来了不利影响. 因此,PID参数的自整定方法仍有发展的空间.
工程实践中,由于对象的模型不易获得,自整定方法的实时性等效果不理想. 因此,更多的是依赖于人的丰富经验,通过观察响应曲线的形状,实时调整PID控制器的3个参数,往往能获得性能指标的理想控制效果. 若利用人的调节经验、主动学习和认知能力去实现PID参数的自整定,而不是人去调整,可能会促进整定方法的发展. 由于案例推理(case-based reasoning,CBR)起源于人的认知心理,它的推理思想符合人类利用积累的经验解决新问题的思路,适用于不易建立对象模型、 但具有丰富经验的推理求解过程[14]. 因此,本文采用CBR研究一种具有学习能力的PID参数认知整定方法,改进了文[15]中的案例检索和案例库的生成机制,重新设计参数整定的结构与功能,获得基于多属性决策思想[16]的案例检索策略. 并运用多目标评价准则[17]对控制效果进行评价与修正,实现整定案例库的自动生成与自学习功能.最后通过对比实验验证该方法的有效性.
2 问题分析PID控制器根据给定值r(t)与输出值y(t)的偏差e(t)输出控制信号u(t),对被控变量进行实时控制.在连续控制系统中,PID的输出u(t)与输入e(t)之间成比例—积分—微分的关系,即:
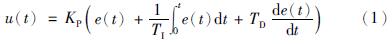
式中,e(t)=r(t)-y(t),KP为比例增益,TI为积分时间,TD为微分时间.
对某个被控对象来说,衡量控制性能的指标包括超调量δ、 稳态误差ess、 调节时间ts、 上升时间tr、 峰值时间tp和衰减比η等,整定式(1)中的PID参数(KP、 TI、 TD)一般是依据上述指标的动态变化情况来设定,可用式(2)描述:
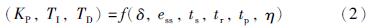
式(2)表示的整定模型难以获得,避开这一问题的方法很多,从最初的Z-N法、 Cohen-Coon法到后来的指标函数优化法、 ISTE最优整定法等都属于经验公式法,通过被控对象的模型参数或响应特性根据经验公式直接求出PID 3个参数. 虽然操作简单,但与调节时间、 超调量等单个性能指标间还缺乏明显的对应关系且模型参数不易辨识,实际应用时不易掌握. 工程整定法虽然可以通过实验获得被控对象的阶跃响应,或者对象本身的特性曲线,但采用衰减曲线法、 临界比例度法或响应曲线法去整定PID参数,其临界稳定点难以确定、 调节时间过长,使得以上方法的适用范围仍然有限.
实践中,往往是依赖于人的经验、 认知和学习能力,通过观察式(2)中性能指标的动态变化情况去整定参数,经验丰富的操作人员往往可以得到合适的PID参数. 因此,有必要将具有这种思想的CBR技术应用于参数调整,以避免经验试凑法的调整繁琐、 实时性能不理想的缺陷. 文[15]实现了这种自整定方法,并取得了一定效果,但案例检索和案例库的生成机制还需改进.
3 CBR认知整定方法基于上述分析,本节设计一种具有主动学习功能的CBR模型,运用多属性决策思想改进案例检索策略,并采用多目标评价准则对控制效果进行评价后修正PID参数,实现案例库的选择性存储,以提高检索的成功率,增强CBR方法的适应性和自学习能力.
3.1 结构与功能从认知角度看,CBR体现了人类记忆、 规划、 学习和问题求解的心理模型,将其应用于PID参数整定的基本思想是: 具有PID调节丰富经验的操作人员,通过观察和认知被控变量响应曲线的变化情况,回忆以往的调整经验并做出自我评价后,选择正确的调整方案. 因此,设计图 1所示的基于CBR的PID认知整定(CTCBR)结构,包括PID控制器、 被控对象、 特征提取模块、 基于多属性决策的案例检索、 案例重用、 多目标案例评价、 案例修正和案例存储等模块. 其中,X={x1,…,x6}表示性能指标集,x1~x6分别表示超调量δ、 稳态误差ess、 调节时间ts、 上升时间tr、 峰值时间tp和衰减比η; X′={x′1,…,x′6}表示期望指标集,x1′~x6′分别表示x1~x6的指标期望值; E={e1,…,e6}表示指标误差集,e1~e6分别表示指标实际值x1~x6与期望值x′1~x′6的误差绝对值; Y={y1,y2,y3}表示解集,y1~y3分别表示PID参数KP、 TI和TD.
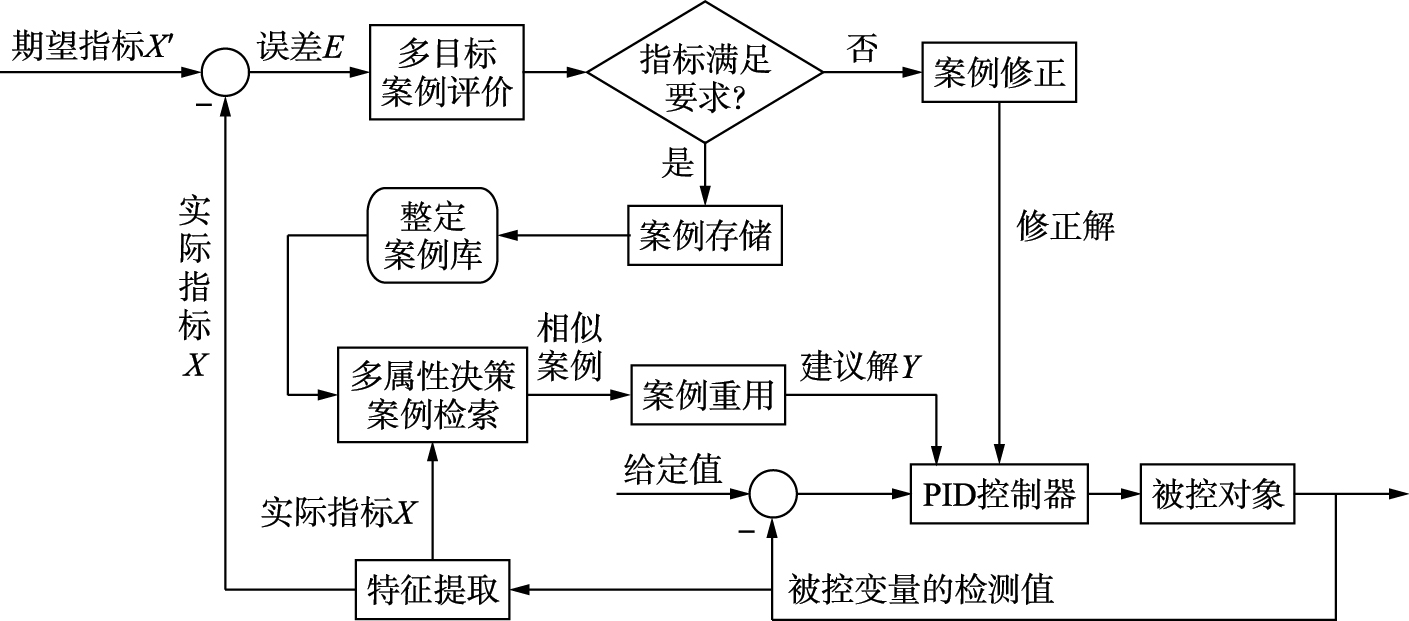 |
| 图 1 基于CTCBR的PID参数整定结构图Fig. 1 PID parameters′ tuning structure diagram based on CTCBR |
当被控变量的检测值发生变化时,通过特征提取得到实际的性能指标X={x1,…,x6},依据多属性决策案例检索策略得到相似案例,并进行案例重用. 将PID参数的建议解Y={y1,y2,y3}输入至PID控制器,作用于被控对象,再次通过特征提取得到建议解的实际指标X,与期望指标X′={x′1,…,x′6}进行比较后得到指标的误差E在案例评价环节,若各项性能指标满足期望值,则按式(2)的映射关系将PID参数和性能指标存储于整定案例库中; 若未全部满足,则进行案例修正,然后将PID参数的修正解输入PID控制器,此时再比较实际指标X与期望指标X′,重复多目标案例评价过程,直到所有性能指标都满足期望值.
3.2 认知整定算法设整定案例库中有p个记录,则第i个记录可表示为如下的二元组形式:
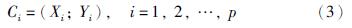
其中,Xi={x1,i,x2,i,…,x6,i}是第i条案例记录的归一化指标值; Yi={y1,i,y2,i,y3,i}是相应于Xi的PID参数整定值.
借鉴认知科学中内省学习机理,建立具有自学习能力的整定案例库. 具体步骤是: 当系统处于初始状态时,首先依据系统的性能指标,估计出初始PID参数,将此3个参数输入控制系统,得到初始的响应曲线. 采集此时的系统性能指标和期望的性能指标进行比较,若全部满足指标要求,则进入案例存储环节,存储方式如式(3)所示; 若未全部满足要求,则进行案例修正,将修正后的PID参数再次输入控制系统,得到修正后的响应曲线,采集修正后的系统性能,与系统要求的性能指标进行比较,步骤同上. 重复以上步骤得到PID参数整定案例库.
当被控变量的指标值发生变化时,可能偏离期望值,需要设置新的PID参数,保证被控变量的稳定控制. 由于整定案例的质量需要根据指标的变化情况去综合评价,这里就涉及到多属性决策问题[17]. 它是一个包含大量认知、 反应和判断的过程,可以将其分为4个阶段,如图 2所示.
 |
| 图 2 多属性决策过程Fig. 2 Multi-attribute decision-making process |
首先,决策者要构造出有待解决的问题. 这一阶段需要确定外部环境和内部构造,建立被控对象的系统仿真模型. 尽可能明确所需解决问题的总任务和准则,并提出相应的备选方案. 本文主要是构造经验案例库. 这一阶段对决策的质量起着至关重要的影响. 其次,要对采集的数据进行预处理,包括数据一致化和无量纲化处理. 然后,根据决策者对方案的偏好,建立各属性的偏好关系. 这一阶段需要确定各属性的效用函数及属性间的偏好关系. 当确定具体偏好值时,采用熵权法确定各属性的偏好值. 最后,通过一定的集结方法对决策方案进行整体评价,由决策者选择满意方案并付诸实施.
采用多属性决策方法实现案例检索时,首先利用基于指标性能的集结方式进行决策值d的计算,即:
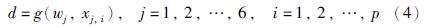
式中,wj为第j个性能指标xj的权重,xj,i是第i条案例记录中的第j个指标的归一值. 再根据多属性决策信息集结方式逐一计算每一个源案例的决策值. 第j个性能指标的权重值可由熵权法[18]计算:

其中,p是整定案例的个数. 于是,第i条案例的决策值采用加权算术平均算子的集结方式[19]得到:

至此,实现了多属性决策检索. 相对于传统CBR使用的K近邻(K-nearest neighbour,KNN)检索,多属性决策方法考虑了每个性能指标的权重,并用以计算检索案例的决策值.
将每条案例的决策值进行排序,设最大决策值为D+,将其对应的案例解作为新案例的初始解去重用,而后进入案例评价与修正阶段.
将基于多属性决策案例检索与重用后的建议解(即PID参数值)输入系统模型,对建议解输入至被控系统后产生的运行状况进行多目标评价[15],若指标精度均满足要求,则输出目标解; 若未能满足要求,则由基于专家规则[15]的方法输出修正值,再次进行上述的综合评价与修正,直至指标误差达到要求.
补偿规则如下所示:
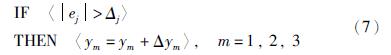
式中,δj表示第j个性能指标xj的误差上限,δym为事先设定的校正值,ym表示第m个参数. 经过案例评价与修正,可以实现推理过程的反馈和调节,确保案例库的动态调整,以增强其自学习能力.
将新问题的描述值X={x1,x2,…,x6}及其相应的整定值Y={y1,y2,y3}存储于案例库中,用于下一次问题的推理求解. 至此,案例记录的总数为p+1个.
3.3 算法步骤综上所述,实现基于案例推理的PID参数认知整定算法步骤为
Step 1:建立PID参数整定案例库.
i) 通过手动调节,得到对应实验对象参数KP、 TI、 TD的大致范围.
ii) 获取被控对象的初始响应曲线并进行特征提取,评价系统性能,若全部满足则得到目标解; 若未全部满足要求,则进行案例修正,对修正解重复评价与修正步骤,直到所有性能指标都满足期望值得到目标解. 最后记录当前PID参数及系统性能指标.
iii) 按事先设定的次数重复以上过程.
iv) 按式(3)所选定的案例表示方法建立自整定案例库.
Step 2:据式(5)计算各指标的权重.
Step 3:由式(6)计算每条案例的决策值,选择决策值最大的案例作为新案例的建议解.
Step 4:由指标误差值进行效果评价,通过仿真输出,判断新案例建议解(或Step 5中修正解)的效果. 若效果理想,转Step 6; 否则转Step 5.
Step 5:由式(7)对设定值进行补偿矫正,输出修正解并转至Step 4.
Step 6:存储目标解至案例库,案例总数由p变为p+1.
4 仿真实验为考察本文方法的应用效果,借助Matlab仿真实验平台进行实验,建立PID控制系统模型,选择Z-N法、 ISTE指标法、 Cohen-Coon法、 鲁棒性整定法(Robust)、 遗传算法(GA)和传统CBR整定法(TTCBR)六种典型的方法与本文方法(CTCBR)进行对比实验. 相对于传统CBR整定PID参数(TTCBR)时使用的KNN检索,本文采用多属性决策思想改进传统的KNN检索策略.
4.1 实验设计选取待寻优参数的初始搜索范围: 1阶系统[KP,TI,TD]=[2.988,4.651 7,0.479 8]和2阶系统[KP,TI,TD]=[1.665,1.829 5,0.378 8]. 本文方法中,整定案例库中的案例总数为80; Z-N法中,当响应曲线波峰间差小于0.000 1倍设定值时,认为是等幅振荡; ISTE法需将对象拟合成1阶惯性环节,拟合误差设为0.01个单位量; GA算法中,种群大小设为30,交叉概率为0.9,变异概率为0.1,做10次实验后取平均值,每次实验的进化代数为50,个体适应度函数定义为
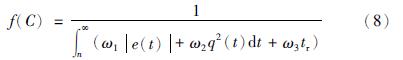
其中,C是个体; e(t)为系统误差; q(t)为控制器输出; tr为上升时间; 权重ε1、 ε2、 ε3表示各个适应因素的比重大小,分别取值为2、 200、 4.
4.2 1阶时滞系统仿真实验结果1阶时滞系统的传递函数为

分别采用Z-N法、 ISTE指标法、 Cohen-Coon法、 鲁棒性整定法(Robust)、 遗传算法(GA)和传统CBR整定法(TTCBR)六种典型的方法与本文方法(CTCBR)进行对比实验,KP、 TI和TD三个参数的整定值如表 1所示,阶跃响应的性能指标超调量δ、 稳态误差ess和调节时间ts如表 2所示.
| 整定方法 | KP | TI | TD |
| Z-N | 2.988 0 | 4.651 7 | 0.479 8 |
| ISTE | 1.940 4 | 1.684 3 | 0.398 7 |
| Cohen-Coon | 0.054 7 | 0.004 5 | 0.004 0 |
| Robust | 0.735 8 | 0.174 6 | 0.124 3 |
| GA | 0.295 9 | 0.108 1 | 0.745 6 |
| TTCBR | 1.720 4 | 0.867 9 | 0.753 3 |
| CTCBR | 1.651 8 | 1.123 1 | 0.458 3 |
| 整定方法 | δ /% | ts /s | ess |
| Z-N | 95.0 | 7.00 | 0.002 |
| ISTE | 13.2 | 3.34 | 8.0E-04 |
| Cohen-Coon | 5.4E-05 | 29.45 | 7.0E-04 |
| Robust | 0 | 40.50 | 0.005 |
| GA | 2.52 | 4.91 | 1.9E-01 |
| TTCBR | 2.65 | 5.60 | 2.0E-04 |
| CTCBR | 1.65 | 1.99 | 1.6E-05 |
由表 2可知,CTCBR方法的超调量δ、 稳态误差ess和调节时间ts均小于Z-N法、 ISTE指标法、GA算法和TTCBR法. 相对于Cohen-coon算法和Robust算法,CTCBR方法的超调量要大一些,但稳态误差ess和调节时间ts具有明显的优势. 综合来看,对于1阶时滞系统,采用本文的CTCBR方法能够得到较理想的性能.
4.3 2阶时滞系统仿真实验结果2阶时滞系统选择文[20]给出的系统,传递函数为
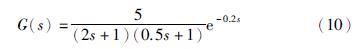
分别采用上述6种方法与本文方法(CTCBR)进行对比实验,KP、 TI、 TD的整定值如表 3所示,阶跃响应的性能指标δ、 ess和ts的结果如表 4所示.
| 整定方法 | KP | TI | TD |
| Z-N | 1.665 0 | 1.829 5 | 0.378 8 |
| ISTE | 2.044 3 | 0.776 3 | 0.200 0 |
| Cohen-Coon | 0.054 7 | 0.004 5 | 0.004 0 |
| Robust | 1.009 3 | 1.934 2 | 0.324 7 |
| GA | 0.315 7 | 0.085 3 | 0.420 7 |
| TTCBR | 1.135 0 | 0.469 5 | 0.325 8 |
| CTCBR | 0.889 4 | 0.226 2 | 0.307 7 |
| 整定方法 | δ /% | ts /s | ess |
| Z-N | 63.82 | 4.17 | 0.015 |
| ISTE | 60.34 | 7.32 | 0.004 |
| Cohen-Coon | 0 | 56.34 | 0.268 |
| Robust | 83.35 | 15.29 | 0.003 |
| GA | 5.15 | 16.20 | 1.1E-04 |
| TTCBR | 15.37 | 4.60 | 1.3E-04 |
| CTCBR | 0.24 | 1.78 | 1.3E-04 |
由表 4可知,CTCBR的超调量δ、 稳态误差ess和调节时间ts均小于Z-N法、 ISTE指标法、 Robust算法和TTCBR法. 相对于Cohen-coon算法,CTCBR方法的超调量要大一些,但稳态误差ess和调节时间ts具有明显的优势. 相对于GA算法,虽然稳态误差ess稍大,但超调量δ和调节时间ts要小许多. 综合来看,对于2阶时滞系统,采用本文的CTCBR方法也能够得到较理想的性能.
综上所述,CTCBR整定方法由于采用多属性决策思想改进案例检索策略,运用多目标评价准则对控制效果进行评价与修正,可以自动生成的整定案例库具有自学习功能. 以上措施保证了整定参数的合理性,可以提高控制性能.
5 结论本文提出的基于案例推理的PID参数认知整定方法借鉴了人的认知心理和主动学习能力,可实现PID参数的实时整定,不需要辨识模型参数及确定临界稳定点. 通过典型一阶和二阶时滞系统的对比实验,性能指标明显改善. 表明融合多属性决策思想与多目标评价的案例推理算法可以提高检索的成功率,具有自学习功能,能够达到预期的控制效果. 下一步的研究方向是研究认知科学中的启发式学习和理解性学习改进案例推理的重用与修正机制,利用人类的记忆与遗忘机理改进案例存储策略等,同时,还需要考虑整定方法应用于实际过程时的算法复杂度问题,以提高整定效率.
| [1] | Tsai S C. Comments on "Robust design of a digital PID predictor controller"[J]. IEEE Transactions on Industrial Electronics, 1985, IE-32(3):268. |
| [2] | 雷飞, 邹益仁. 一种基于PID的实时控制与调度协同设计方法[J]. 信息与控制, 2004, 33(5):541-543. Lei F, Zou Y R. A PID based real-time control and scheduling co-design approach[J]. Information and Control, 2004, 33(5):541-543. |
| [3] | Jung J W, Leu V Q, Do T D, et al. Adaptive PID speed control design for permanent magnet synchronous motor drives[J]. IEEE Transactions on Power Electronics, 2014, 30(2):900-908. |
| [4] | 王永刚, 柴天佑. 强制循环蒸发系统的非线性自适应解耦PID控制[J]. 控制理论与应用, 2011, 28(9):1145-1153. Wang Y G, Cai T Y. Nonlinear adaptive decoupling PID control for the forced-circulation evaporation system[J]. Control Theory & Applications, 2011, 28(9):1145-1153. |
| [5] | Andrikopoulos G, Nikolakopoulos G, Manesis S. Advanced nonlinear PID-based antagonistic control for pneumatic muscle actuators[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12):6926-6937. |
| [6] | Lee J Y, Jin M, Chang P H. Variable PID gain tuning method using backstepping control with time-delay estimation and nonlinear damping[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12):6975-6985. |
| [7] | Li H. Application of PID-type iterative learning control for DC motor[J]. Computer Modelling and New Technologies, 2014, 18(5):247-251. |
| [8] | Ziegler J G, Nichols N B. Optimum settings for automatic controllers[J]. Journal of Dynamic Systems, Measurement and Control, 1993, 115(2B):220-222. |
| [9] | Shridhar R, Cooper D J. A novel tuning strategy for multivariable model predictive control[J]. ISA Transactions, 1997, 36(4):273-280. |
| [10] | 汪浩, 李晓明, 严伟, 等. 具有最小时间加权平方误差积分的主动队列管理算法ISTE-PI[J]. 计算机学报, 2012, 35(5):951-963. Wang H, Li X M, Yan W, et al. A novel AQM algorithm based on the PI controller with minimum ISTE[J]. Chinese Journal of Computers, 2012, 35(5):951-963. |
| [11] | 曹建秋, 徐凯. 遗传算法优化的模糊+变论域自适应模糊PID复合控制策略[J]. 信息与控制, 2011, 40(1):44-49. Cao J Q, Xu K. Compound control strategy of fuzzy+variable universe self-adaptive fuzzy-PID based on genetic algorithm optimization[J]. Information and Control, 2011, 40(1):44-49. |
| [12] | Chee F, Fernando T L, Savkin A V, et al. Expert PID control system for blood glucose control in critically ill patients[J]. IEEE Transactions on Information Technology in Biomedicine, 2003, 7(4):419-425. |
| [13] | 葛金来, 张承慧, 崔纳新. 模糊自整定PID控制在三自由度直升机实验系统中的应用[J]. 信息与控制, 2010, 39(3):342-347. Ge J L, Zhang C H, Cui N X. Fuzzy self-tuning PID controller in the 3-DOF helicopter experimental system[J]. Information and Control, 2010, 39(3):342-347. |
| [14] | Aamodt A, Plaza E. Case-based reasoning-foundational issues, methodological variations, and system approaches[J]. AI Communications, 1994, 7(1):39-59. |
| [15] | Yan A J, Chai T Y, Yu W, et al. Multi-objective evaluation-based hybrid intelligent control optimization for shaft furnace roasting process[J]. Control Engineering Practice, 2012, 20(9):857-868. |
| [16] | Charilas D E, Panagopoulos A D, Markaki O I. A unified network selection framework using principal component analysis and multi attribute decision making[J]. Wireless Personal Communications, 2014, 74(1):147-165. |
| [17] | Khamis M A, Gomaa W. Adaptive multi-objective reinforcement learning with hybrid exploration for traffic signal control based on cooperative multi-agent framework[J]. Engineering Applications of Artificial Intelligence, 2014, 29(3):134-151. |
| [18] | Li L, Liu F, Li C B. Customer satisfaction evaluation method for customized product development using entropy weight and analytic hierarchy process[J]. Computers and Industrial Engineering, 2014, 77(11):80-87. |
| [19] | 董玉成, 徐寅峰, 王扬. 基于广义Fuzzy偏好关系的决策方法探讨[J]. 系统工程学报, 2008, 23(3):282-288. Dong Y C, Xu Y F, Wang Y. Study of decision making method using generalized fuzzy preference relations[J]. Journal of System Engineering, 2008, 23(3):282-288. |
| [20] | Xiu Z H, Ren G. Optimization design of TS-PID fuzzy controllers based on genetic algorithms[C]// Proceedings of the Fifth World Congress on Intelligent Control and Automation.Piscataway, UJ, USA:IEEE, 2004:2476-2480. |



