2. 沈阳化工大学信息工程学院, 辽宁沈阳 110142
2. College of Information Engineering, Shenyang University of Chemical Technology, Shenyang 110142, China
1 引言
为了满足现代社会瞬息万变的市场需求,现代过程工业正逐渐倚重于小批量、 多批种、 高附加值产品的间歇生产过程,针对间歇过程的过程监测、 故障诊断及质量预测研究已成为目前相关领域的研究热点[1, 2].
近年来多元统计控制的方法已广泛应用到间歇过程监测中,如多向主元分析法(MPCA),多向偏最小二乘法(MPLS)[3, 4, 5]. 这些建模方法将间歇操作的所有数据当作一个样本,虽然能有效地监视过程的整体运行情况,却很难进一步分析间歇过程内部数据的动态特征,这使得基于MPCA的过程监测算法对幅值较小的故障不慎敏感,而且大多数与主元分析/偏最小二乘(PCA/PLS)相关的数据描述方法都存在数据服从高斯分布和不同变量关系是线性的限制,在线的过程监测算法在很大程度上依赖于对未来测量值预估的准确程度等问题. 目前针对在线间歇生产过程监视存在实时性的问题,也相继提出了最小窗口主元分析法、 基于子时段的主元分析建模等方法[6, 7, 8]. 但这些方法都没能解决数据服从高斯分布的限制,而一些能够处理非高斯、 非线性数据的方法,如多向独立元分析方法(MICA)、 核独立主元分析方法(KICA)虽然能获取非高斯的数据信息,但仍存在由于初值选取的随机性导致检测结果的不稳定性、 如何选取独立元、 计算量大等问题[9, 10, 11]. 因此这些方法对于间歇过程的监测效果都不理想.
20世纪90年代末Tax等提出了支持向量数据描述(SVDD)方法,该方法通过非线性转换将正常数据样本空间映射到高维特征空间建立模型,并且没有数据服从高斯分布的限制,能够应用到变量间是非线性关系的数据中,因此在工业生产过程中的应用越来越广泛[12, 13, 14, 15, 16, 17, 18]. 该方法虽然在处理非高斯、 非线性数据中表现出了极大的优势,但是仍存在在线间歇过程监测实时性不佳的问题.
针对上述问题,本文综合考虑了数据存在非高斯、 非线性的限制和在线监测实时性不佳的问题,提出了一种基于滑动窗口的SVDD建模方法. 当实时故障监测时,该方法采用适当大小的滑动窗口逐步更新当前的子数据空间; 然后分别建立SVDD模型. 该方法既解决了数据非高斯、 非线性的限制,同时又考虑了间歇过程数据的内部动态特性,提高了在线间歇过程监测的实时性. 本文首先对复杂的间歇过程数据进行数据预处理; 然后,根据不同的窗口宽度大小更新子数据空间进行建模; 最后在数值仿真、 青霉素发酵实验及半导体生产过程中加以应用,结果表明取得了良好的监测效果.
2 SVDD基本理论SVDD的基本思想是针对数据集X={xi,i=1,…,N},通过非线性转换Φ: X→F将原始空间数据投影到特征空间{Φ(xi),i=1,…,N,从而找到一个几乎包含所有数据样本的最小体积超球体. 假定a是超球体的球心,R为超球体半径; 考虑测量误差或者噪音等干扰引起的离群点影响,引入松弛因子ξ;C是惩罚参数,该问题可描述为[10, 11, 12, 13, 14, 15, 16]
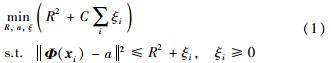
上述优化问题可以转化为解决相应的对偶问题:
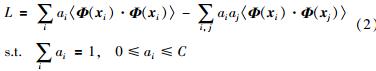
其中ai是拉格朗日因子.
用核函数K(xi·xj)代替内积〈Φ(xi)·Φ(xj)〉以实现低维空间的非线性问题向高维空间的线性问题的转换,可得到:
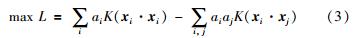
利用二次规划,可以求出ai,如果0 < ai < C,则说明目标数据在超球面上,此时该点为支持向量; 如果ai=0,则说明目标数据在超球体内;如果z是支持向量,则超球体的半径和球心为
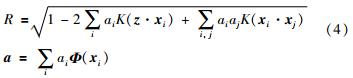
对于新来的样本xnew,其到超球体球心的距离可表示为
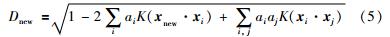
如果Dnew < R则该样本正常; 反之,该样本为异常样本.
3 基于滑动窗口SVDD的建模与监测 3.1 建立模型基于滑动窗口的SVDD(以下简称MWSVDD)建模方法可以分为2个步骤,即数据预处理和模型建立.
(1) 数据预处理
1) 将3维数据X(I×J×K)按时间片方向展开成2维数据X(I×JK).
2) 对展开后的数据进行窗口宽度大小确定,并对每一个窗口内的数据进行标准化处理.
(2) 模型建立
对每一个窗口内的数据应用本文第2节的原理分别建立SVDD模型.
对于基于滑动窗口的建模方法,窗口宽度是一个非常重要的参数. 显然一个大的数据窗口可以建立一个比较稳定可靠的局部SVDD模型,但是该模型却对过程中发生的异常工况反应迟钝,不利于快速的故障监测和诊断; 反过来,小的数据窗口可以提供快速故障监测的能力,但是过短的数据窗口很难建立稳定可靠的SVDD模型,以至于基于小数据窗口的SVDD模型在线监测程序中的故障误报率大大增加,本节建模方法折中考虑了局部模型稳定性和快速故障监测这两个对立的建模要求,窗口长度设定为过程变量个数J的2~5倍. 为了快速监测故障,窗口的滑动步长可以设定为最小值1.
在本文中,假设窗口宽度设为2J,步长设为1. 当第1个时刻到来时,不足以凑成一个完整的窗口宽度,此时选用窗口宽度为J来建模; 当第2个时刻到来时,可以凑成一个完整的窗口数据,选用相应窗口宽度的数据建模与监测,此后窗口按步长1进行滑动. 因此,每一次间歇操作过程产生K个数据窗口,对每一个窗口的数据Xk(I×n×J)(n为窗口宽度)进行如下标准化处理:
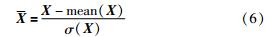
其中,mean(·)为数据阵的平均值,σ(·)为数据阵的标准方差.
标准化之后,每个变量在每个数据窗口中均值为0、 方差为1,去除了数据非线性特性并避免测量值不同量纲的影响.
3.2 监测过程(1) 新样本监测
对于新的数据样本,在其对应的窗口模型下按照式(5)计算其到SVDD超球体球心的距离.
(2) 故障诊断
将计算的距离D与其所对应窗口模型的半径R进行比较:如果D < R,则该样本正常; 反之,说明此数据为故障数据.
MWSVDD建模和在线监测的具体流程[11, 12, 13, 14, 15, 16, 17, 18, 19]如图1所示.
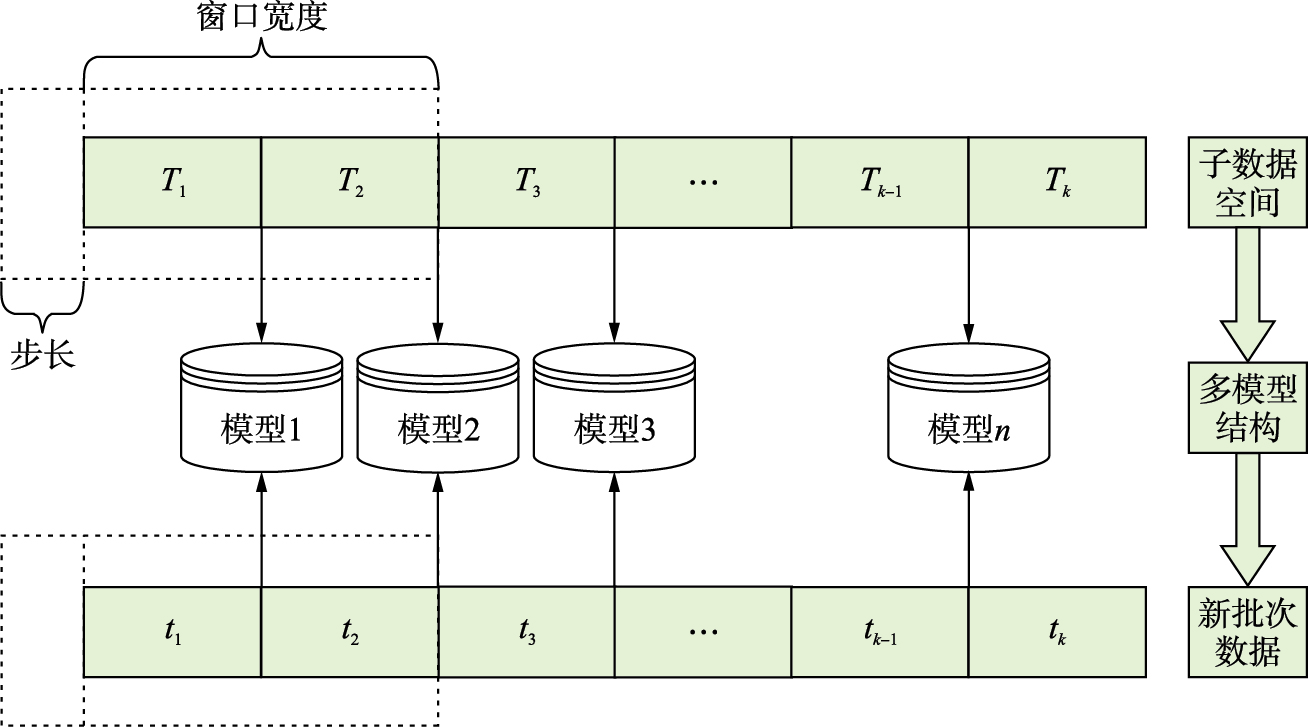 |
| 图 1MWSVDD建模与监测原理图 Fig. 1 Scheme of MWSVDD modeling and monitoring |
首先给了一个数值仿真的例子,然后又分别利用青霉素仿真和半导体的例子进行了实验,验证了MWSVDD方法的有效性、 准确性.
本文采用的核函数均为高斯核函数,计算公式如式(7)所示. 核宽度δ以及惩罚系数C的选择均采用交叉验证的方法取得.
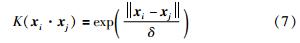
批次过程数据产生如式(8)所示[12]:
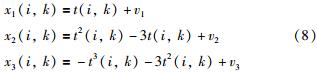
其中i是批次,k是时间常数,x1、x2、x3为3个变量,t满足0.01~2的均匀分布,v1、v2、v3是随机噪声,满足均值为0、方差为0.01的高斯分布,一共产生30批数据,每一批数据包括50个采样点.
构造一个故障批次如式(9)所示,在第1个变量的第25个时刻开始加入斜坡故障.
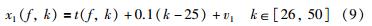
分别利用SVDD(δ=25,C=0.08)和MWSVDD(δ=30,C=0.08,窗口宽度为2)进行监测,结果如图2所示,其中虚线代表控制限,以下所有图均以虚线作为控制限.
 |
| 图 2故障批次的监测结果 Fig. 2 Monitoring results of the faulty batch |
由图2可知,直接使用SVDD在第33个时刻才能监测出故障,但MWSVDD在第28个时刻即监测出故障,由此看出MWSVDD对故障更加敏感、 监测效果更佳.
4.2 青霉素发酵过程监视本文利用青霉素仿真软件[19, 20]产生50批正常数据和3批次的故障数据,都设置为370个采样时刻,在50批正常数据中选取前48批作为建模数据,而剩余的2批正常数据和3批故障数据作为监视批次.
青霉素共有17个变量,选取其中9个变量,如表1所示. 3个批次的故障分别设置为: 对变量1的100~370采样时刻加8%的阶跃故障; 对变量1的100~200采样时刻加3%斜坡故障; 对变量2的100~200采样时刻加3%的斜坡故障. 分别用SVDD(δ=150,C=0.03)和MWSVDD(δ=200,C=0.03,窗口宽度为3)进行监测,结果如图3所示.
| 变量号 | 变量名称 | 变量号 | 变量名称 | 变量号 | 变量名称 |
| 1 | 曝气量 | 4 | 生物量浓度 | 7 | pH值 |
| 2 | 搅拌功率 | 5 | 培养基体积 | 8 | 温度 |
| 3 | 底物浓度 | 6 | 二氧化碳浓度 | 9 | 冷却水流量速率 |
 |
| 图 3 青霉素数据故障批次监测结果 Fig. 3 Monitoring results of the Penicillin data faulty batch |
从图3可知,MWSVDD能够对故障进行快速监测,特别是对于改善由于斜坡故障的延迟效应所带来的监测实时性不高的问题,取得了良好的效果.
4.3 半导体数据本文采用的研究数据是从一个实际的半导体制造过程采集而来[12, 13],该过程一共进行了3组实验,共得到129批数据,其中包括108批正常工况下的数据和21批故障数据. 通过对数据的初步分析,发现有两批过程的数据缺失情况比较严重,去掉这两批不完整数据之后,一共有107批正常数据和20批故障数据,为了对该过程进行监测,一共选取了17个过程变量. 本文选取99批作为建模数据,8批用于验证模型的准确性. 在对过程数据进行分析和预处理之后,得到3维数据矩阵X(I×J×K),每一批数据含有85个采样点. 本文采用一批正常样本数据验证建模的准确性,分别代入SVDD(δ=75,C=0.03)和MWSVDD(δ=360,C=0.03,窗口宽度为4)进行监测,结果如图4所示.
 |
| 图 4 正常批次监测结果 Fig. 4Monitoring results of the normal batch |
由图4可知,利用MWSVDD建立模型的准确性较高,没有产生误报. 本文列举了第19和第20批故障数据的监测效果,如图5所示.
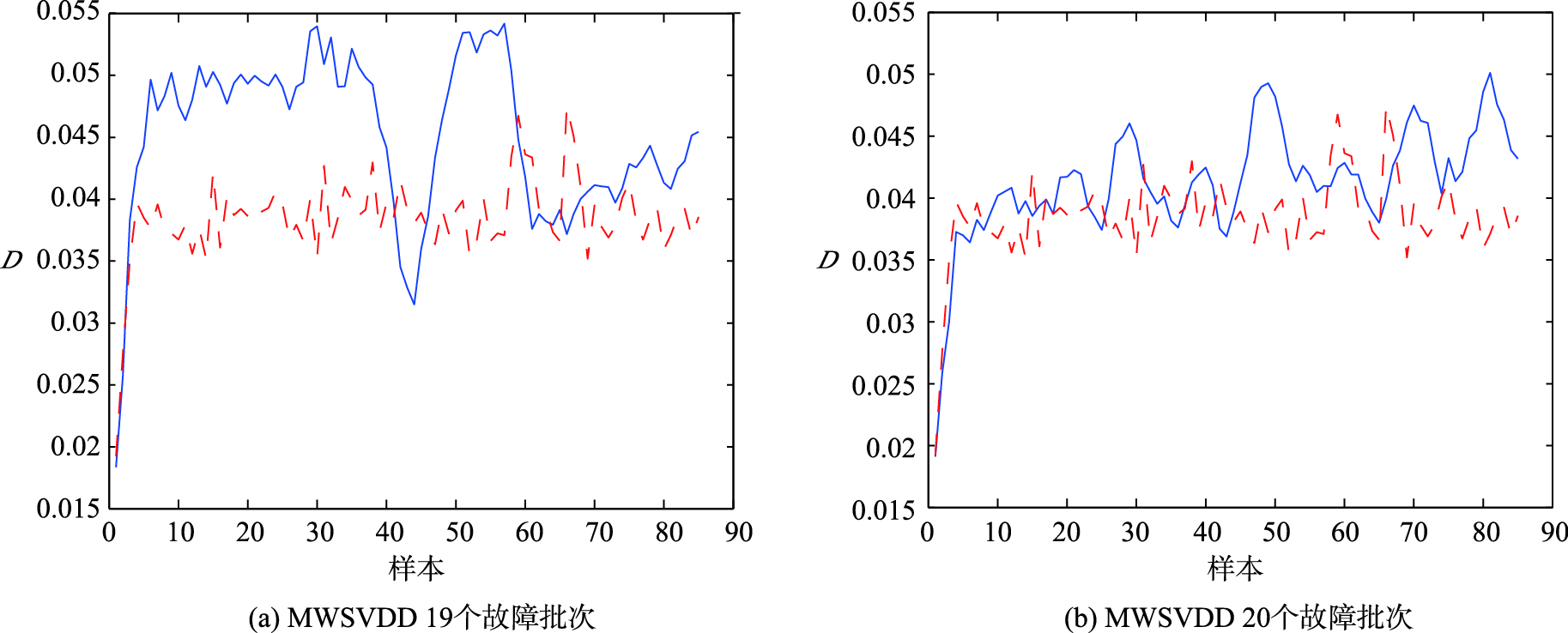 |
| 图 5 滑动窗口故障批次的监测结果 Fig. 5 Monitoring results of the moving window faulty batch |
为了体现不同窗宽对监测效果的影响,本文分别对8个正常批次的半导体数据及20批故障数据用不同的窗口宽度一一作了监测,结果分别如表2和表3所示.
| 批次 | MWSVDD | 批次 | MWSVDD | ||||||
| 窗宽为2 | 窗宽为3 | 窗宽为4 | 窗宽为5 | 窗宽为2 | 窗宽为3 | 窗宽为4 | 窗宽为5 | ||
| 1 | 0.129 | 0.118 | 0.106 | 0.141 | 6 | 0.059 | 0.024 | 0.000 | 0.012 |
| 2 | 0.035 | 0.035 | 0.035 | 0.024 | 7 | 0.082 | 0.071 | 0.035 | 0.094 |
| 3 | 0.047 | 0.012 | 0.000 | 0.000 | 8 | 0.071 | 0.071 | 0.035 | 0.047 |
| 4 | 0.059 | 0.082 | 0.012 | 0.012 | 平均 | 0.072 | 0.057 | 0.031 | 0.044 |
| 5 | 0.094 | 0.047 | 0.024 | 0.024 | |||||
| 批次 | SVDD | MWSVDD | 批次 | SVDD | MWSVDD | ||||||
| 窗宽为2 | 窗宽为3 | 窗宽为4 | 窗宽为5 | 窗宽为2 | 窗宽为3 | 窗宽为4 | 窗宽为5 | ||||
| 1 | 0.435 | 0.600 | 0.624 | 0.682 | 0.671 | 12 | 1.000 | 0.988 | 1.000 | 1.000 | 1.000 |
| 2 | 0.118 | 0.341 | 0.341 | 0.353 | 0.435 | 13 | 1.000 | 0.988 | 1.000 | 1.000 | 1.000 |
| 3 | 0.024 | 0.106 | 0.047 | 0.024 | 0.035 | 14 | 0.188 | 0.447 | 0.506 | 0.541 | 0.600 |
| 4 | 1.000 | 0.988 | 1.000 | 1.000 | 1.000 | 15 | 0.047 | 0.129 | 0.071 | 0.059 | 0.035 |
| 5 | 0.012 | 0.024 | 0.047 | 0.024 | 0.024 | 16 | 0.282 | 0.706 | 0.694 | 0.777 | 0.800 |
| 6 | 0.000 | 0.012 | 0.012 | 0.012 | 0.012 | 17 | 0.094 | 0.200 | 0.118 | 0.129 | 0.106 |
| 7 | 1.000 | 0.988 | 1.000 | 1.000 | 1.000 | 18 | 0.906 | 0.941 | 0.988 | 0.977 | 0.988 |
| 8 | 0.141 | 0.553 | 0.541 | 0.659 | 0.706 | 19 | 0.576 | 0.824 | 0.871 | 0.835 | 0.859 |
| 9 | 0.059 | 0.129 | 0.118 | 0.071 | 0.094 | 20 | 0.271 | 0.682 | 0.635 | 0.706 | 0.788 |
| 10 | 0.306 | 0.388 | 0.365 | 0.424 | 0.471 | 平均 | 0.380 | 0.514 | 0.511 | 0.524 | 0.543 |
| 11 | 0.141 | 0.235 | 0.235 | 0.200 | 0.235 | ||||||
由表2和表3可知,窗口宽度为4或5时效果都挺好,但窗宽为5时误报率相对于窗宽为4时提高了41.9%,而检测率仅仅提高了3.6%,故认为当窗宽为4时,监测效果最好,并且与SVDD相比,监测结果有了很大的提升.
5 结论基于滑动窗口的SVDD方法是一种应用于复杂非线性间歇过程中具有实时在线监视的方法. 该方法的主要思想是采用适当大小的滑动窗口逐步更新当前的子数据空间,然后分别建立SVDD模型,多个子空间模型构成了整个间歇过程动态模型集合. 将该方法应用到数值仿真、 青霉素发酵过程仿真实验及实际的半导体生产过程实验中,都取得了良好的效果. 说明基于滑动窗口的SVDD方法针对间歇过程具有良好的故障监测能力,能够考虑间歇过程数据的内部动态特性,并且能够克服数据服从高斯分布和不同的变量之间关系是线性的限制. 这对在线监测过程中监视实时性不佳的问题有了很大的改善.
| [1] | 王姝,常玉清,王福利,等. 时段划分的多向主元分析间歇过程监测及故障变量追溯[J]. 控制理论与应用,2011,28(2):149-156. Wang S,Chang Y Q,Wang F L,et al. Multiway principle component analysis monitoring and fault variable detection based on substage separation for batch processes[J]. Control Theory & Applications,2011,28(2):149-156. |
| [2] | 常鹏,王普,高学金. 基于核熵投影技术的微生物制药生产过程监测[J]. 信息与控制,2014,43(4):490-494. Chang P,Wang P,Gao X J. Microbial pharmaceutical process monitoring based on projection kernel entropy component[J]. Information and Control,2014,43(4):490-494. |
| [3] | Hoskuldsson A. PLS regression methods[J]. Journal of Chemometrics,1988,2(3):211-228. |
| [4] | Nomikos P,Macgregor J F. Monitoring batch processes using multiway principal component analysis[J]. American Institute of Chemical Engineers Journal,1994,40(8):1361-1375. |
| [5] | Chen J,Liu J. On-line batch process monitoring using dynamic PCA and dynamic PLS models[J]. Chemical Engineering Science,2002,57(1):63-75. |
| [6] | 周东华,李钢,李元. 数据驱动的工业过程故障检测与诊断技术[M]. 北京:科学出版社,2011. Zhou D H,Li G,Li Y. Data-driven based process fault detection and diagnosis technology[M]. Beijing:Science Press,2011. |
| [7] | Qin J S. Survey on data-driven industrial process monitoring and diagnosis[J]. Annual Reviews in Control,2012,36(2):220-234. |
| [8] | Lee J M,Yoo C,Lee I B. Fault detection of batch processes using multiway kernel principal component analysis[J]. Computers & Chemical Engineering. 2004,28(9):1837-1847. |
| [9] | 赵春晖,王福利,姚远,等. 基于时段的间歇过程统计建模、 在线监测及质量预报[J]. 自动化学报,2010,36(3):366-374. Zhao C H,Wang F L,Yao Y,et al. Phase-based statistical modeling,online monitoring and quality prediction for batch process[J]. Acta Automatica Sinica,2010,36(3):366-374. |
| [10] | Lennox B,Montague G A,Hiden H G,et al. Process monitoring of an industrial fed-batch fermentation[J]. Biotechnology and Bioengineering,2001,74(2):125-135. |
| [11] | Ge Z Q,Song Z H. Performance-driven ensemble learning ICA model for improved non-Gaussian process monitoring[J]. Chemometrics and Intelligent Laboratory Systems,2013,123(15):1-8. |
| [12] | Ge Z Q,Gao F R,Song Z H. Batch Process monitoring based on support vector data description method[J]. Journal of Process Control,2011,21(6):949-959. |
| [13] | Ge Z Q,Song Z H. Bagging support vector data description model for batch process monitoring[J]. Journal of Process Control,2013,23(8):1090-1096. |
| [14] | Tax D M J,Duin R P W. Support vector domain description[J]. Pattern Recognition Letters,1999,20(11/12/13):1191-1199. |
| [15] | Tax D M J,Duin R P W. Support vector domain description[J]. Machine Learning,2004,54(1):45-66. |
| [16] | 谢彦红,耿志成,李元. SVDD在间歇过程监测中的应用研究[J]. 计算机与应用化学,2013,30(12):1401-1405. Xie Y H,Geng Z C,Li Y. Research on the appliance of support vector data description method in batch process monitoring[J]. Computers and Applied Chemistry,2013,30(12):1401-1405. |
| [17] | Yao Y,Gao F R. Phase and transition based batch process modeling and online monitoring[J]. Journal of Process Control,2009,19(5):816-826. |
| [18] | 熊伟丽,肖应旺,徐保国. 基于特征子空间的滑动窗PCA在批过程故障诊断中的应用[J]. 计算机与应用化学,2006,23(4):303-306. Xiong W L,Xiao Y W,Xu B G. Batch process fault diction based on characteristic subspace moving window PCA[J]. Computers and Applied Chemistry,2006,23(4):303-306. |
| [19] | 刘世成,王海清,李平. 青霉素生产过程的在线统计检测与产品的质量控制[J]. 计算机与应用化学,2006,23(3):227-232. Liu S C,Wang H Q,Li P. On-line statistical monitoring and production quality control of penicillin cultivation process[J]. Computers and Applied Chemistry,2006,23(3):227-232. |
| [20] | 刘毅,王海清. Pensim仿真平台在青霉素发酵过程中的应用研究[J]. 系统仿真学报,2006,18(12):3524-3527. Liu Y,Wang H Q. Pensim simulator and its application in penicillin fermentation process[J]. Journal of System Simulation,2006,18(12):3524-3527. |



