1 引言
密集脉冲序列分选在雷达信号处理领域一直备受关注[1, 2, 3]. 随着雷达技术的发展,变化类型复杂的雷达脉冲信号日益增多,同时信号环境日益密集和交叠,这使得雷达信号分选任务日趋艰巨和困难. 传统的分选方法主要有动态关联法[4]、 累计差直方图法[4](CDIF)、 序列差直方图法[5](SDIF)、 PRI变换法[6, 7, 8, 9]及一些改进算法[10, 11, 12, 13, 14, 15]. 当遇到脉冲重复周期(PRI)变化无明显规律,不能利用统计特征进行提取时,这些方法显得无能为力. 平面变换技术[16]是依据累计变换的数学原理,将时间维的脉冲序列变换到二维的时间平面,再利用不同变化类型脉冲信号在平面图像上的不同显示特征达到去交错目的的一种分选方法. 然而,已有的平面变换方法或是通过人工方法完成不同脉冲信号的提取工作[17],实时性较差;或是受脉冲序列的密度影响较大[1],在当今脉冲序列交叠情况严重的情况下并不适应;或是对PRI变化规律性较强或抖动较小的脉冲序列提取效果较好[16],对脉间滑变的脉冲信号提取没有研究.
本文通过分析脉间线性滑变脉冲信号的成形规律,提出一种脉冲序列时延—样本子图外推提取算法. 该算法通过计算全脉冲序列整体时延,求取脉冲相关相关函数峰值点,进而提取滑变信号的样本子图;然后通过样本子图外推搜索的方法提取全脉冲序列中该样本子图对应的脉冲序列,实现滑变信号的提取.
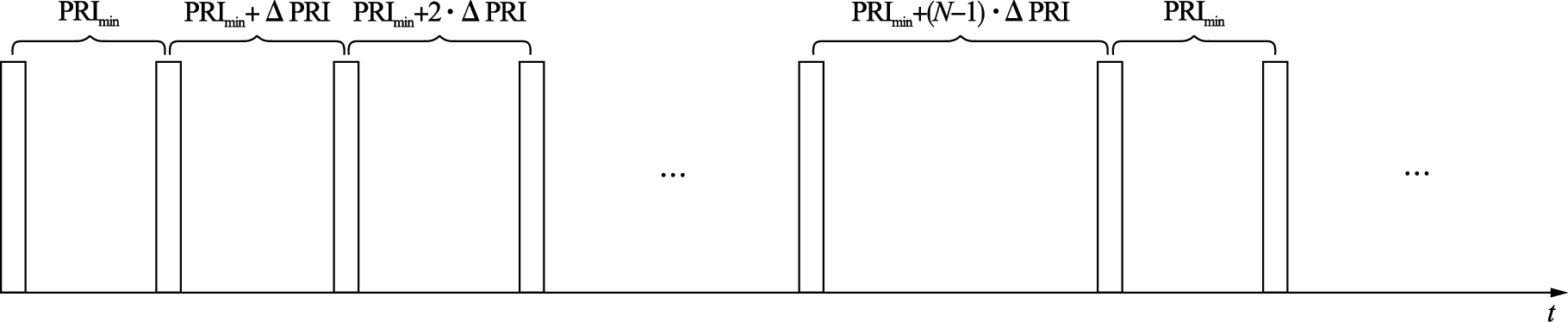
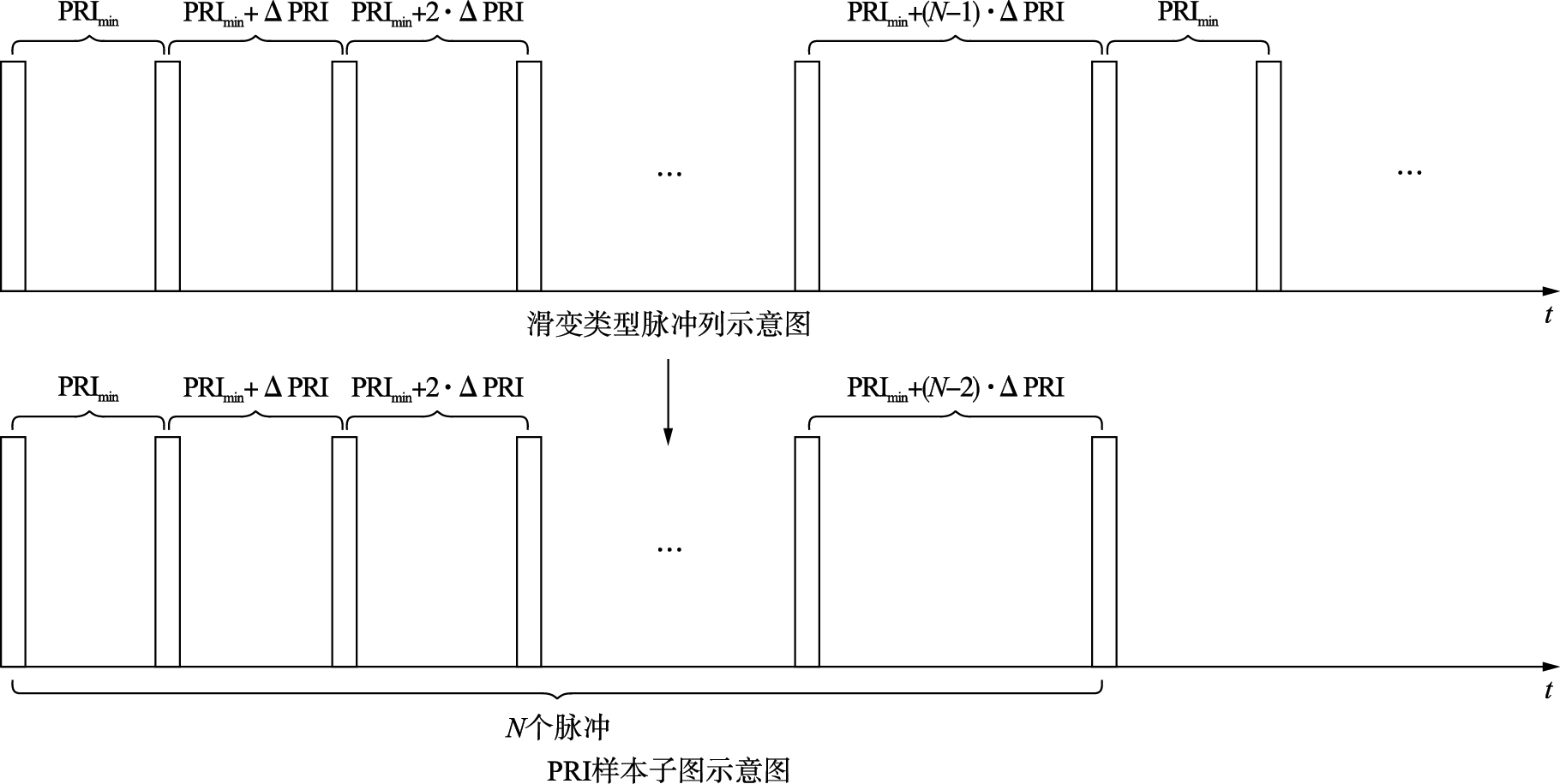
2 PRI滑变脉冲信号的成形规律分析 2.1 滑变脉冲信号PRI成形规律PRI滑变信号是一种脉冲重复周期以固定的差值缓慢地周期性重复变化的信号[18]. 依据PRI的变化趋势,有递增性滑变和递减性滑变之分,每两个相邻脉冲间隔之间的变化值一般很小,且变化值保持不变. 对于PRI递增性滑变信号而言,当其PRI变化达到最大值时会突变至最小值;PRI递减性滑变信号与之相反,之后会重新开始新的变化周期. 此过程不断地重复执行. 以PRI递增性滑变脉冲序列为例来进行说明,图1所示为一PRI递增性滑变脉冲信号在时间轴上的脉冲波形分布图.
 |
| 图 1 重频滑变信号时域特点示意图 Fig. 1 Time domain characteristics diagram of PRI linear slide signal |
图中PRImin是该滑变信号的最小脉冲重复周期,N是滑变周期内的脉冲个数,一般情况下脉冲个数大于2,ΔPRI是基本滑变间隔,该滑变信号的最大脉冲重复周期PRImax=PRImin+(N-2)·ΔPRI. 设接收机接收到的该滑变信号的首脉冲到达时间为T0,假定该脉冲同时为某一滑变周期的首脉冲,T(i)表示第i个脉冲的到达时间,则T(i)可表示为

式中, 表示向下取整函数,mod(a,b)表示取余函数,Tframe表示一个滑变周期的持续时间,易知:
表示向下取整函数,mod(a,b)表示取余函数,Tframe表示一个滑变周期的持续时间,易知:

同理可知,对于递增性滑变脉冲信号,T(i)可表示为
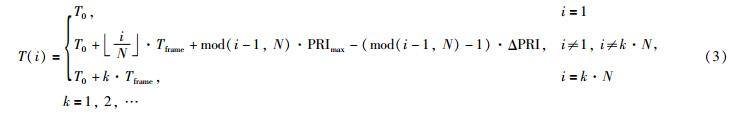
由滑变脉冲信号的PRI成形规律可以看出,可以表征滑变脉冲信号的参数主要是脉冲重复间隔的极值(最大值或最小值)和基本滑变间隔. 如何通过对交迭脉冲列的变换处理提取出其中滑变脉冲信号的脉冲重复间隔极值和基本滑变间隔,是提取滑变脉冲信号的关键.
2.2 滑变脉冲序列时延规律 假设存在一组递增性滑变脉冲信号序列Y,仅包含时间维特征参数脉冲到达时间(TOA),脉冲个数为M. 则Y可表示为
将滑变脉冲信号进行时延处理,是指将脉冲列沿时间轴整体延迟一定的时间间隔,即全脉冲整体平移处理. 将脉冲列整体时延τ间隔后的表达式为
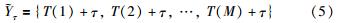
定义两脉冲时间相关函数f(T(i),T(j))为

两脉冲序列的相关函数RX(τ)定义为
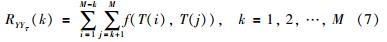
为了减少运算量,不计算随机的连续时延. 上式中将随机时延采用脉冲列移位维数k表示,将自相关函数表示为离散的形式. 于是,当接收机接收到的全脉冲序列中含有某一个滑变信号脉冲列时,脉冲列沿时间轴延迟该信号的一个周期,即τ=Tframe. 此时,将延迟后的全脉冲序列与原始脉冲序列进行时间相关,计算时间窗σ内匹配上的所有脉冲,所得到的相关函数必定会出现峰值. σ为根据脉冲列密度和脉冲到达时间精度设置的时间窗宽度,σ≥0.
3 序列时延—样本子图外推提取方法 3.1 序列时延相关处理按照2.2节的定义,当全脉冲整体时延τ为移位n个脉冲的移位间隔,即τ=DTOA(n)=T(n+1)-T(1),0 ≤ n < M,DTOA(n)表示第n+1个脉冲与第1个脉冲的时间差,则 可表示为
可表示为
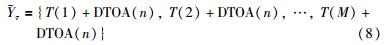
定义函数δ(a,b,ε):

式中,ε≥0. 则根据定义,可以求得当延时n个脉冲时的相关函数为

脉冲样本图用一串(多个)脉冲的特征参数来描述雷达的知识特征[19],而雷达脉冲样本子图(pulse sequence subpattern,PSS)是雷达脉冲样本图在低维空间上的投影. 引入雷达脉冲样本子图的目的有两个:一是有的雷达的脉冲样本图在某一维或几维上是恒定不变的,这时,用样本子图可使描述更简便,处理更方便;二是有时为了分析方便,可以将复杂的样本图通过投影得到简化,使其在分析中可以抓主要矛盾,提高分选、 分析的效率. 脉冲样本子图描述技术是脉冲样本图描述技术的扩展和简化.
样本子图用参数序列来描述脉冲重复周期特征参数的变化规律,是对雷达某一种工作模式下时间维变化特征的一种描述. 通常情况下,雷达的PRI特征参数是周期性变化的,若选取该特征参数的一个变化周期作为样本模板,就能准确地对脉冲到达时间这一维参数进行描述,这个样本模板就是PRI样本子图.
对于雷达情报侦察而言,侦察设备获得的雷达信号实际上是一个脉冲序列信号[21],该脉冲序列中的某一个特征参数序列可以记录为

通常X都是周期序列,从X中选取一个周期的序列,也就是一个能准确表示整个序列的最小子序列X′,即:

把该子序列中取值相同的相邻脉冲进行合并,并记录取值相同脉冲的数量,则有:

显然有n1+n2+…+nm=l. 如果把脉冲重复周期参数的变化类型记录在此子序列中,这样就得到了雷达某一种工作模式下的脉冲样本子图,表示如下:

Xi表示的是第i种工作模式下的脉冲样本子图,c表示脉冲重复周期参数的变化类型. 图2所示为一个最小脉冲重复周期为PRImin,滑变周期内的脉冲个数为N,基本滑变间隔为ΔPRI的滑变类型信号的样本子图示意图. 根据定义,其样本子图可表示为

式中,5是滑变信号类型标识.
 |
| 图 2 重频滑变信号样本子图示意图 Fig. 2 PSS schematic diagram of PRI slide signal |
当相关函数出现峰值时,通过脉冲时间相关函数值和移位脉冲序列,可以提取该滑变信号的样本子图. 本节阐述如何利用样本子图进行外推,提取该滑变信号的所有脉冲,并对该序列的时间维参数进行估计.
利用序列时延—样本子图外推进行滑变信号提取的具体步骤如下:
(1) 利用序列时延相关进行样本子图提取. 将序列时延用移位位数表征,移位后的脉冲序列生成时间窗口,然后寻找原始序列中落在时间窗口内的脉冲. 当脉冲序列时延达到某一个滑变信号的整周期时,相关函数值会出现峰值,此时若相关函数值满足:

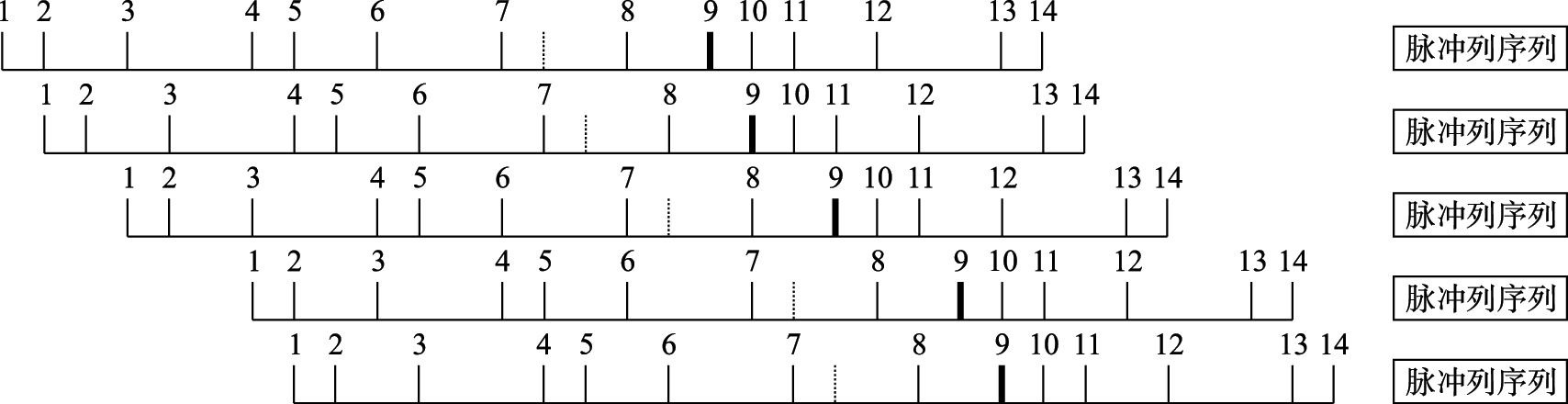
则可以提取该滑变信号的样本子图. 式中,符号“∩”表示各式之间是“与”的关系,Rthreshold为相关函数峰值门限. 脉冲序列时延相关示意图如图3所示,某一个滑变信号的时间窗口生成及样本子图提取示意图如图4所示.
 |
| 图 3 脉冲序列时延和相关示意图 Fig. 3 The schematic diagram of pulse sequence time delaying and correlation |
 |
| 图 4 时间窗口和样本子图提取示意图 Fig. 4 The schematic diagram of time-window and PSS extracting |
(2) 样本子图时延搜索提取对应脉冲序列. 假设通过时延相关,得到某一滑变信号的样本子图为

则该滑变信号的周期为Tframe,样本子图可提取的脉冲个数为K+1. 选择原始脉冲序列中首脉冲T(1)为基准脉冲,按照Xi中PRI值进行外推搜索,若原始脉冲列中第i个脉冲的到达时间T(i)满足:

则判定为此脉冲到达时间落在时间窗口内,脉冲匹配成功. 接下来,更新此脉冲为基准脉冲继续寻找,搜索原始脉冲序列中是否有第j个脉冲的到达时间T(i)满足:

若原始脉冲序列中未搜索到满足式(18)条件的i脉冲,则将时间窗口更新为T(1)+T1+T2-σ,T(i)+T+1T2+σ,继续向后寻找.
在一个样本子图周期匹配完成后,进行一次周期匹配成败判断. 设一个周期内匹配上的脉冲数目为Lp,计算Lp/(K+1)的值,若Lp/(K+1)>λ(λ为匹配门限值),则匹配成功,记录匹配脉冲;否则,判别为匹配失败,当连续匹配失败次数达到3次,这次提取不成功,重新进行序列时延计算相关函数值.
(3) 样本子图外推补充漏失脉冲. 在进行样本子图外推时,计算Lp/(K+1),若Lp/(K+1) < λ,则未完全匹配,即原始脉冲序列中匹配上的此样本子图周期内有漏脉冲,补上此漏脉冲,漏脉冲的到达时间参数为样本子图中对应的搜索脉冲到达时间. 漏脉冲补充完毕后,重新寻找基准脉冲,继续进行匹配,并记录匹配脉冲和补充脉冲.
(4) 匹配脉冲列提取. 当搜索脉冲到达时间满足T(i)+T1+σ > T(M)且Lp/(K+1) > λ,则提取所有记录的匹配脉冲,此次样本子图外推提取结束.
(5) 去除已提取脉冲,若剩余脉冲大于脉冲数目门限值M′,继续进行时延相关,并重复上述步骤.
4 脉冲序列提取实验实际接收的雷达脉冲环境很复杂,经常掺杂大量的干扰脉冲[1]. PRI线性滑变脉冲信号是一种常见的雷达信号,因此研究该类型雷达脉冲的自动提取方法是很有价值的. 为了检验算法在复杂背景的信号环境下的提取性能,仿真实验产生参数不同的多种雷达交迭脉冲,尽可能接近真实信号环境. 同一实验重复100次,4次实验为一组,共得到25组平均实验结果. 通过得到的平均实验结果研究不同的信号环境对本文算法提取效果的影响,即对脉冲提取正确率、 漏选率的影响. 相关定义为
(1) 正确率:(SR/S)·100%,其中S是提取到的属于同一雷达的脉冲数目,SR为其中正确的脉冲数目.
(2) 漏选率:((SM-SR)/SM)·100%,其中SM表示全脉冲数据中某一雷达的真实脉冲数目.
仿真实验环境:Windows XP,Intel 1.8 G,1 G内存,工具为Matlab.
4.1 多个线性滑变脉冲信号混迭的提取实验考虑全脉冲序列中包括10%~15%的干扰脉冲,并且有一定的脉冲漏失. PRI受线性调制的脉冲序列有3个,调制初始值分别为:100 μs、 200 μs、 250 μs;一个调制周期内脉冲数分别为:20、 15、 25;基本滑变间隔分别为:5 μs、 3 μs、 2 μs;PRI线性调制类型分别为:递增性、 递减性. 干扰脉冲随机插入线性滑变脉冲序列. 门限值设定:时间窗口宽度σ=1 μs,剩余脉冲M′=40 个,λ=0.6.
首先进行脉冲的序列时延相关,搜索自相关函数的极大峰值,提取对应滑变脉冲序列的样本子图. 图5所示为自相关函数值随着全脉冲移位位数n(即序列时延)的变化曲线.
 |
| 图 5 自相关函数变化曲线 Fig. 5 The curve of autocorrelation function |
从图5可以看出,当全脉冲循环移位位数n=45时,自相关函数出现个极大峰值,此时可以提取此雷达信号的样本子图. 在提取样本子图后,利用该样本子图为模板进行后续外推,将对应时间点上的脉冲提取出来,实现该部雷达信号对应脉冲的提取,在提取过程中,若依据样本子图中本应有脉冲存在的时间点却无脉冲,则此处为丢失脉冲位置. 图6所示为提取进行过程中自相关函数的不断变化情况. 图6(a)所示为提取出一部雷达信号以后对剩余脉冲进行第2次全脉冲匹配的自相关函数变化曲线. 当提取出两部雷达信号以后,继续进行第3次循环相关时,自相关函数变化曲线如图6(b)所示.
 |
| 图 6 自相关函数变化曲线图 Fig. 6 The curves of autocorrelation function |
采用同样步骤对剩余脉冲继续进行循环移位相关,在提取样本子图的同时分选出对应的雷达信号. 表1为自提取的3个样本子图及其维数,由表1结果可以看出,3种信号的参数特征和变化规律均能从样本子图中得到. 待所有信号提取完毕后,通过统计可以得到各脉冲序列的平均提取正确率和平均漏选率分别如图7和图8所示.
| 提取出的雷达编号 | 自提取的样本子图 /μs | 样本子图维数 |
| Radar_1 | PSS1={[100, 100],[105, 105],[110, 110]…,[190, 190];1,1,…,1;5} | 19 |
| Radar_2 | PSS2={[200, 200],[203, 203],[206, 206]…,[239, 239];1,1,…,1;5} | 14 |
| Radar_3 | PSS3={[250, 250],[252, 252],[254, 254]…,[296, 296];1,1,…,1;5} | 24 |
 |
| 图 7 各信号平均提取正确率 Fig. 7 The average extraction accuracy of the signals |
 |
| 图 8各信号平均漏选率 Fig. 8 The average loss rate of the signals |
从上述实验来看,由于受到随机干扰脉冲的影响,各个信号的平均提取正确率稍有不同,但是最低的脉冲信号提取正确率仍能达到95%,验证了序列时延—样本子图外推提取算法对线性滑变脉冲能够实现有效的提取. 表2所示为进行100次蒙特卡罗实验后,对3种滑变脉冲信号提取的结果进行平均后的统计.
| 雷达 编号 | 真实 脉冲数 | 干扰脉冲处理后 真实脉冲数 | 平均提取 脉冲数 | 补充脉冲 个数 | 平均提取 正确率 /% |
| Radar_1 | 1 000 | 981 | 1000 | 19 | 100.0 |
| Radar_2 | 1 000 | 969 | 992 | 23 | 99.2 |
| Radar_3 | 1 000 | 912 | 954 | 42 | 95.4 |
由表2结果可知,利用样本子图外推算法提取脉冲时,由于干扰脉冲影响丢失的脉冲,大部分会被补充进来,以保证滑变脉冲序列的完整性. 3号雷达之所以最后提取效果较差是因为丢失脉冲数相对较多,利用样本子图进行外推补充时,若外推一个周期,对应的时间点窗口内均无脉冲,即全部丢失,此时不进行漏脉冲补充的而继续向后外推,因此造成提取正确率稍差一些.
4.2 与经典分选算法提取性能比较考虑全脉冲序列中包括10%~15%的干扰脉冲,并且有一定的脉冲漏失. 1 000个PRI受线性调制的脉冲序列,在调制周期内有20个脉冲,调制初始值为100 μs,采用递增线性滑变,基本滑变间隔为5 μs. 其余为一个PRI固定类型脉冲序列,PRI为210 μs. 采用经典的PRI变换算法与本文算法分别对脉冲序列进行处理. 图9和表3分别为PRI变换方法和本文方法对数据处理的结果,表3所示为两种进行100次蒙特卡罗实验统计出来的结果. 由图9和表3的结果表明,PRI变换法仅能将PRI固定类型脉冲序列提取出来,对于PRI线性滑变类型脉冲信号未能准确提取,而本文算法能够将两种脉冲信号准确提取出来. 需要说明的是,PRI固定类型脉冲序列相当于线性滑变信号的特殊形式,即基本滑变间隔为0 μs;PRI变换法是基于对PRI值的统计特征进行提取,因此对于PRI值较多的脉冲序列处理效果不理想.
| 信号类型 | 真实脉冲数 | 平均提取脉冲数/平均提取正确率 | |
| 本文算法 | PRI变换算法 | ||
| PRI线性滑变 | 1 000 | 1 000/100% | -(无结果) |
| PRI固定 | 1 000 | 1 000/100% | 999/99.9% |
 |
| 图 9 PRI变换法分选效果图 Fig. 9 Sorting results of PRI transform algorithm |
本文提出一种脉冲序列时延—样本子图外推提取算法. 该算法基于滑变信号成形规律和滑变脉冲序列的样本子图特点,通过全脉冲序列整体时延,求取相关函数峰值点,进而提取滑变信号的样本子图,并提出通过样本子图外推搜索的方法提取全脉冲序列中该样本子图对应的脉冲序列,实现滑变信号的提取. 实验结果表明该算法对线性滑变脉冲序列的平均提取正确率能够达到95%. 在经典PRI变换法无法有效提取的情况下,该算法仍能以较高正确率实现对PRI线性滑变脉冲信号的提取. 下一步针对如何提高算法的实时性,实现线性滑变信号的快速且准确地提取,会做进一步的研究.
| [1] | 樊甫华, 张万军, 谭营. 基于累积变换的周期性对称调制模式的快速自动搜索算法[J]. 电子学报, 2005, 33(7): 1266-1270. Fan F H, Zhang W J, Tan Y. A fast and automatic searching algorithm of periodic and symmetric patterns based on accumulative transformation technique[J]. Acta Electronica Sinica, 2005, 33(7): 1266-1270. |
| [2] | Pace P E. Detecting and classifying low probability of intercept radar[M]. Norwood: Artech House, 2009: 31-37. |
| [3] | Nishiguchi K, Kobayashi M. Improved algorithm for estimating pulse repetition intervals[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(2): 407-421. |
| [4] | 杨学永, 宋国栋, 钱轶, 等. 现代雷达信号分选跟踪的几种方法[J]. 现代雷达, 2014, 36(3): 43-48. Yang X Y, Song G D, Qian Y, et al. Several methods of radar signal sorting and tracking[J]. Modern Radar, 2014, 36(3): 43-48. |
| [5] | 易波, 刘培国, 薛国义. 一种基于顺序差值直方图算法的改进雷达信号分选方法[J]. 舰船电子对抗, 2012, 35(1): 6-10. Yi B, Liu P G, Xue G Y. An improved method for radar signal sorting based on SDIF histogram algorithm[J]. Shipboard Electronic Countermeasure, 2012, 35(1): 6-10. |
| [6] | Mahdavi A, Pezeshk A M. A fast enhanced algorithm of PRI transform[C]//Proceedings of 2011 6th International Symposium on Parallel Computing in Electrical Engineering, Piscataway, NJ, USA: IEEE, 2011: 179-184. |
| [7] | Tian F F. De-interleaving of radar signal based on improved PRI transform algorithm[J]. Electronic Science and Technology, 2010, 23(11): 116-118. |
| [8] | 李英达, 肖立志, 于洋, 等. 一种新的PRI变换分选算法[J]. 科学技术与工程, 2014, 14(12): 209-213. Li Y D, Xiao L Z, Yu Y, et al. A new algorithm of PRI transform[J]. Science Technology and Engineering, 2014, 14(12): 209-213. |
| [9] | Deng B, Qin Y L, Wang H Q, et al. SFM signal detection and parameter estimation based on pulse-repetition-internal transform[C]//2012 Proceedings of the 20th European Signal Processing Conference (EUSIPCO). Piscataway, NJ, USA: IEEE, 2012: 1855-1859. |
| [10] | 黄宇, 刘锋, 王泽众, 等. 基于FRFT的雷达信号chirp基稀疏特征提取及分选[J]. 航空学报, 2013, 34(2): 393-400. Huang Y, Liu F, Wang Z Z, et al. Chirp function sparse feature extraction and sorting of radar signals based on FRFT[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2): 393-400. |
| [11] | 李英达, 肖立志. 一种脉冲重复间隔复杂调制雷达信号分选方法[J]. 电子与信息学报, 2013, 35(10): 2494-2497. Li Y D, Xiao L Z. A method of signal sorting for radar signal of pulse repetition interval complex modulated[J]. Journal of Electronics & Information Technology, 2013, 35(10): 2494-2497. |
| [12] | 陈维高, 张国毅. 基于直方图和脉冲关联的抖动信号分选算法[J]. 现代防御技术, 2014, 42(3): 142-148. Chen W G, Zhang G Y. Novel jitter signal sorting algorithm based on histogram and pulse associating[J]. Modern Defence Technology, 2014, 42(3): 142-148. |
| [13] | 陈维高, 张国毅, 常硕. PRI周期性调制信号的TOA中点匹配分选算法[J]. 现代防御技术, 2014, 42(4): 125-230. Chen W G, Zhang G Y, Chang S. TOA center matching sorting algorithm of PRI periodic modulation signal[J]. Modern Defence Technology, 2014, 42(4): 125-230. |
| [14] | 梁华东, 韩江洪. 采用双谱多类小波包特征的雷达信号聚类分选[J]. 光子学报, 2014, 43(3): 1-8. Liang H D, Han J H. Clustering and sorting radar signals based on multi-wavelet packets characteristics of bispectrum[J]. Acta Electronica Sinica, 2014, 43(3): 1-8. |
| [15] | Aziz A M. A novel and efficient approach for automatic classification of radar emitter signals[C]//Proceedings of 2013 IEEE Aerospace Conference. Piscataway, NJ, USA: IEEE, 2013: 1-8. |
| [16] | 张西托, 饶伟, 杨泽刚, 等. 平面变换技术脉冲分选自动实现方法[J]. 数据采集与处理, 2012, 27(4): 495-500. Zhang X T, Rao W, Yang Z G, et al. Automatic fulfillment of deinterleaving pulses based on plane transformation[J]. Journal of Data Acquisition & Processing, 2012, 27(4): 495-500. |
| [17] | 赵闯, 赵拥军, 李东海. TOA折叠平面特征点无监督聚类[J]. 现代雷达, 2010, 32(1): 39-41. Zhao C, Zhao Y J, Li D H. Characteristic points unsupervised clustering on TOA folding plot[J]. Modern Radar, 2010, 32(1): 39-41. |
| [18] | 潘继飞, 姜秋喜. 一种脉间滑变雷达信号特征提取新方法[J]. 电子信息对抗技术, 2011, 26(1): 9-13. Pan J F, Jiang Q X. A new method of feature extraction of inter-pulse sliding radar signal[J]. Electronic Information Countermeasure Technology, 2011, 26(1): 9-13. |
| [19] | 旷平昌, 王杰贵, 罗景青. 基于脉冲样本图和Vague集的辐射源辐射源识别[J]. 宇航学报. 2011, 32(7): 1639-1644. Kuang P C, Wang J G, Luo J Q. Radar emitter recognition based on pulse sequence pattern and vague set[J]. Journal of Astronautics, 2011, 32(7): 1639-1644. |
| [20] | 孟祥豪, 罗景青, 王杰贵. 基于自提取脉冲样本图的辐射源信号快速提取法[J]. 航天电子对抗, 2014, 30(4): 53-57. Meng X H, Luo J Q, Wang J G. A rapid extraction method of radar signals based on self-extraction pulse sequence pattern[J]. Aerospace Electronic Warfare, 2014, 30(4): 53-57. |
| [21] | 关一夫, 张国毅, 刘志鹏. 一种基于脉冲样本序列的PRI周期信号分选算法[J]. 电讯技术, 2014, 54(7): 915-920. Guan Y F, Zhang G Y, Liu Z P. A novel de-interleaving algorithm for PRI periodic signal based on pulse sample sequences[J]. Telecommunication Engineering, 2014, 54(7): 915-920. |



