1 引言
并联机械手具有惯量低、刚度大、负载能力强等优点，已广泛用于诸如分拣、抓取和包装等高重复高强度操作中. 但当并联机械手按照规定的任务进行轨迹运动时，由于存在加工误差和装配误差，使得理想运动轨迹与实际运动轨迹之间存在误差，由此造成并联机械手定位不准确、轨迹运动精度低等问题. 为此，国内外许多学者对并联机械手的运动学参数辨识标定进行了研究. 文[1, 2, 3, 4, 5, 6]分别利用球杆仪、三坐标测量机、激光跟踪仪和计算机视觉作为测量手段对并联机械手进行了运动学标定. 但这类标定需要专业技术人员来操作这些测量仪器，采集数据过程繁琐且设备成本高； 文[7]采用最小二乘法直接进行标定计算，但计算量大，且需要额外进行轨迹优化计算； Levenberg-Marquardt算法[8]综合牛顿法和最陡下降法的优点，虽然计算速度较快、局部收敛性能较好，但对计算机硬件要求较高且易陷入局部最优解； 而粒子群优化算法具有较好的全局和局部搜索能力. 为此，本文以Delta并联机械手为例，利用改进的粒子群优化算法对其进行运动学参数辨识，并通过仿真实验验证算法的有效性和可行性.
2 Delta并联机械手误差建模 2.1 误差源分析图1为Delta并联机械手3维模型，由动、静平台和3条对称布置的支链组成. 各支链中，主动臂与静平台通过转动副连接，从动臂为一个平行四边形结构，各杆通过球铰连接. 在3个电机的驱动下，可实现动平台的3维平动. 在实际应用中，可以通过合理制造和装配工艺来保证从动臂的平行四边形结构[3]. 于是，可将模型简化为图2所示(以第1支链为例). 机械手运动学模型中的静态误差主要为零部件的加工误差和装配误差，图中，O-XYZ为静平台上的固定坐标系，O′-X′Y′Z′为固定于动平台上的动坐标系，Ai、Ci分别为主动臂与静平台、从动臂与动平台的连接位置，Bi为主动臂与从动臂的连接位置，OAi、AiBi、BiCi、O′Ci分别为静平台半径、主动臂长、从动臂长和动平台半径，几何尺寸分别为R、L、K、r，相应的加工误差分别为ΔRi、ΔLi、ΔKi、Δri； θi为主动臂与静平台平面OXY的夹角，即为电机转过的角度，记顺时针为正，其对应的装配误差是并联机械手关节角度传感器安装位置和定义的关节零点位置之间存在的一个偏角，记作Δθi，αi、βi分别为OAi、O′Ci与坐标轴OX、O′X′的夹角，理论上αi=βi=-π/6+2π(i-1)/3，对应的装配误差为Δαi、Δβi(i=1，2，3). 但文[9]分析发现机构装配误差对操作端(O′点)误差的影响程度远大于加工误差对操作端误差的影响. 在实际应用中，加工误差ΔRi、ΔLi、ΔKi、Δri也可通过精密的加工和测量手段得到其近似精确值，故本文选取Δθi、Δαi、Δβi(i=1，2，3)九项主要误差源来建立Delta并联机械手的运动学误差模型.
 |
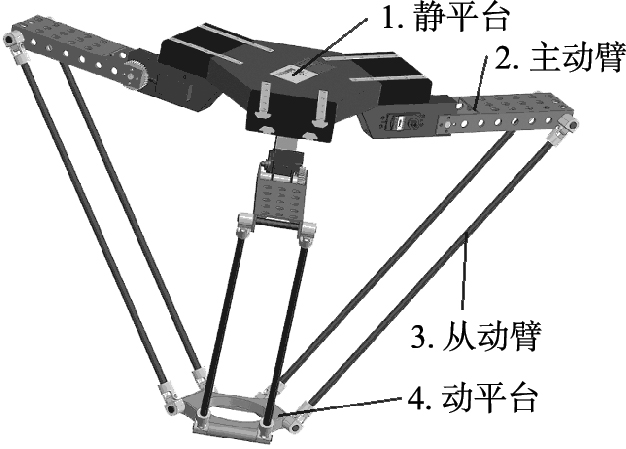| 图 1 Delta并联机械手3维模型 Fig. 1 3D model of Delta parallel manipulator |
 |
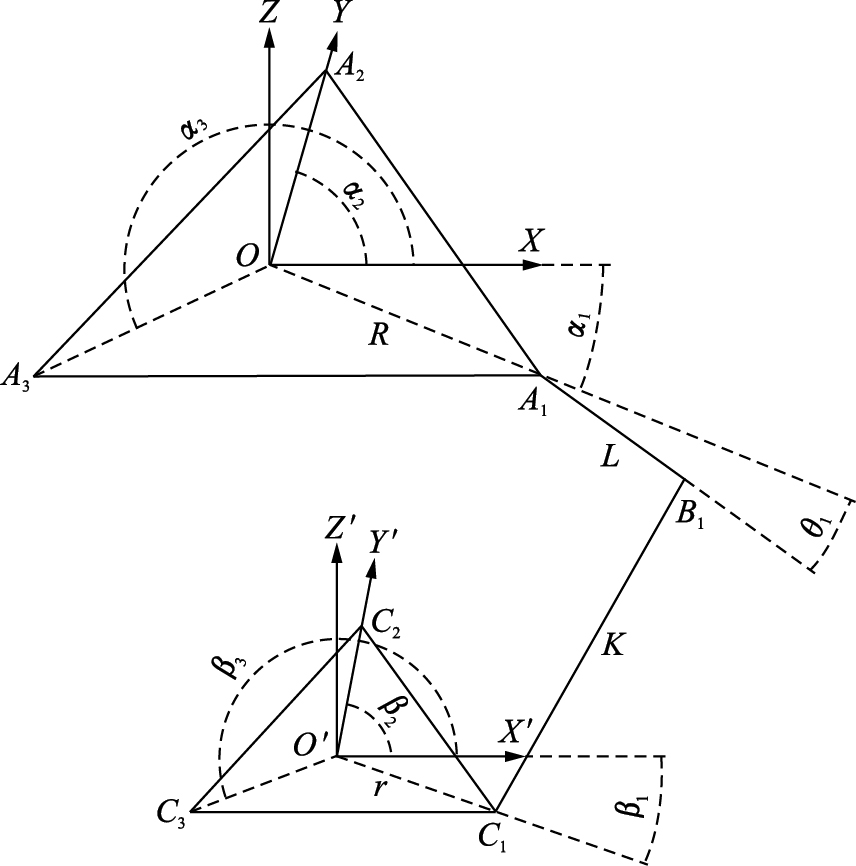| 图 2 第1支链机构简图 Fig. 2 Mechanism sketch of the first chain |
设A(A1，A2，A3)点是电机驱动关节所在的点，则向量OA可表示为
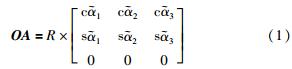
其中，s表示正弦函数sin，c表示余弦函数cos.
同理，主动臂方向的向量AB可表示为
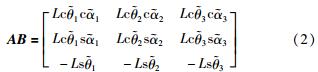
从动臂末端C点在坐标系O′中的向量O′C可以表示为
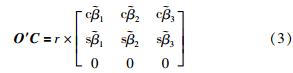
设动平台中心点O′在坐标系O下的坐标为(Px，Py，Pz)，则点C在坐标系O下的坐标为
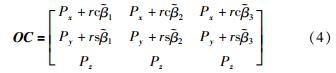
根据模数相等可得
，即：
由此可得如式(6)的闭链约束矩阵：
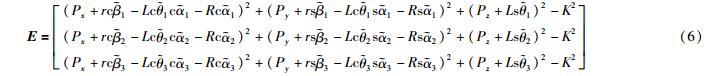
其中，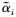
=αi+Δαi，
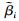=βi+Δβi，
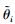=θi+Δθi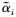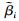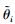，、、为实际值，αi、βi、θi为理想值，Δαi、Δβi、Δθi为误差值，即需要辨识的参数. r、R、L、K、Px、Py、Pz单位均为mm，其余变量单位均为rad.
理论上，当Δαi=Δβi=Δθi=0时，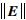
应该是严格等于0的，但实际上由于装配不准确使得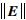值的大小由装配误差所决定. 并联机械手的参数辨识就是通过选取机械手的若干位形作为采样点，计算各采样点所对应的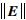值，通过对装配误差进行辨识，并将辨识出的误差代入式(6)，最终使得采样点对应的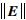值尽可能接近于0. 因此，可建立如下的误差函数[10]，即为后述改进粒子群优化中的适应度函数：
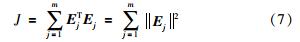
式中，m为采样点个数，J是m个采样点的误差之和，通过使其达到最小来得到待辨识的误差参数值.
3 基于粒子分类和按维动态改变权重的改进粒子群算法 3.1 标准粒子群算法模型粒子群优化(particle swarm optimization，PSO)算法是由Eberhart和Kennedy于1995年提出的一种全局优化算法[11]. 假设在一个D维的搜索空间中，由n个粒子组成一个群体，其中第i个粒子(i=1，2，…，n)表示为Xi=(xi1，xi2，…，xiD)，即第i个粒子在D维搜索空间中的位置为Xi. 换言之，每个粒子的位置就是一个潜在的解，其中，第d维的位置记为xid(d=1，2，…，D)，将Xi代入目标函数就可以计算出其适应度值. 根据适应度值的大小衡量其优劣，如果它所经过的最好位置记为Pi=(pi1，pi2，…，piD)，则整个群体所有粒子经历过的最好位置可记为Pg=(pg1，pg2，…，pgD).
由Shi和Eberhart[12]在标准PSO基础上引入惯性权重ω，得到如式(8)、(9)描述的PSO算法：
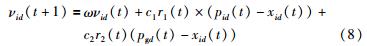
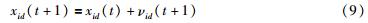
式中，t表示迭代次数，c1和c2为加速度常数，c1为调节粒子向自身最优位置pid(t)飞行的步长，c2为调节粒子向全局最优位置pgd(t)飞行的步长，r1和r2为在[0, 1]范围内变化的两个相互独立的随机数； vid(t+1)为粒子下一步迭代的步长，也称为粒子飞行速度，vid∈[-vmax，vmax]，即粒子的速度被一个最大速度vmax所限制； ω为惯性权重，控制着前一个速度对当前速度的影响. 当ω较大时，全局搜索能力较强； ω较小时，局部搜索能力较强. 通过调整惯性权重ω的大小，可以跳出局部极值.
由于PSO算法控制参数少，实现较简单，非常适用于求解大量非线性、不可微和多峰值的连续复杂函数的优化问题. 因此，PSO已在多个学科和工程领域得到了广泛的应用，国内外的研究者做了大量的工作，并提出了许多改进的算法. 但与其它全局优化算法类似，PSO算法还是同样存在早熟收敛、求解精度不高等问题. 为此，提出如下所述的改进算法.
3.2 改进的粒子群优化算法 3.2.1 基于粒子分类进行异步进化的策略以求全局最小值为例，将第t次迭代中所有粒子的适应度值相加取平均值，称为平均极值，假设为favr，按照个体极值、平均极值和全局极值的更新策略更新式(8)的PSO速度. 以平均极值favr为界，进行粒子分类，并采用如下的异步进化策略： 将适应度f(Xi)>favr的粒子(称为劣等粒子)按照式(10)进行速度更新：
将适应度f(Xi)≤favr的粒子(称为优等粒子)按照式(11)进行速度更新：
式中，pavrd(t)为第t次迭代时所有粒子第d维的平均值，即pavrd(t)=(p1d(t)+p2d(t)+…+pnd(t))/n.
引入平均极值将粒子分类，并针对不同粒子采用不同的进化策略，相比标准的PSO算法，劣等粒子更多地借鉴了种群中其它粒子的飞行经验，由全局最优pgd(t)改为平均最优pavrd(t)来引导飞行，充分共享个体最优pid(t)和平均最优pavrd(t)的信息，利用更多的种群信息来决策自己的行为； 而对优等粒子则按照标准模式进行速度更新，以保持向全局最优发展的态势，通过这种异步进化策略可增加种群中粒子的多样性，促进种群协作，有利于减轻早熟收敛现象，极大地改进了算法收敛到全局最优的性能.
3.2.2 基于粒子维差异动态改变惯性权重的策略Shi等[13]提出了惯性权重线性递减PSO(Linearly decreasing weight PSO，LPSO)算法，这一线性递减策略符合寻优中先快速找到较优解然后再进行细致搜索以找到最优解的基本思想，而且为此后对惯性权重的研究产生了深远的影响. 随后，文[14, 15, 16, 17, 18, 19, 20]相继给出了惯性权重关于迭代次数非线性变化的表达式. 但很多对惯性权重的改进忽视了同一个粒子不同维数所具有的搜索差异. 这直接导致了同一代种群中所有粒子的所有维具有相同的惯性权重，使得算法求解精度变差，这是因为即使粒子的某一维达到了最优解，而其它维由于选择了过大或者过小的惯性权重而跳出了最优解区域. 因此应该根据实际问题，考虑同一粒子所具有的维差异来选择惯性权重，以使算法的性能能够有新的突破.
本文引入距离因子的概念，提出了一种基于粒子维差异动态改变惯性权重的策略，如式(12)~(15)：
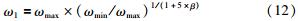
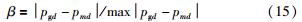
式中，β称为距离因子，即当代最优粒子与当前粒子对应维度状态之间的距离|pgd-pmd|、当代最优粒子与当代所有粒子对应维度状态之间的距离最大值max|pgd-pmd|的比值，m表示第m个粒子，m=1，2，…，N； d表示粒子的维度，d=1，2…，D； pmd表示第m个粒子的第d维状态； pgd表示当前迭代次数下，最优粒子所对应的第d维状态，ωmin为惯性权重最小值，ωmax为惯性权重最大值.
结合3.2.1节所提的粒子分类策略，对惯性权重ω的选择策略如下所述：
对适应度f(Xi) > favr的劣等粒子，当pmd < pgd时，令惯性权重ω=ω1； 否则ω=ω3.
对适应度f(Xi) ≤ favr的优等粒子，当pmd < pgd时，令惯性权重ω=ω2； 否则ω=ω3.
式(12)是一个凹函数，式(13)是一个凸函数. 由式(15)可知，0 ≤ β ≤ 1，且β越大，表示当前粒子距离最优粒子越远，对应ω越大，以保证粒子以较快速度收敛到最优解； 相反，β越小，表示当前粒子距离最优粒子越近，对应ω越小，以保证粒子在当前位置附近进行更细致的搜索，进而得到全局最优解. 另外，对劣等粒子，当pmd < pgd时，选取式(12)来改变权重是因为其在前期具有较大的ω且变化较快，能够快速收敛到最优解； 对优等粒子，当pmd < pgd时，选取式(13)来改变权重是因为其在前期具有较大的ω且变化较慢，为了维持算法的全局搜索能力，需后期变化较快，加速算法的局部寻优能力，从而取得更好的求解效果.
3.3 改进的粒子群算法步骤基于以上的分析，本文改进算法利用平均极值对粒子进行分类，针对不同粒子采用异步进化策略，可提高种群多样性，并增加种群间的协作，使粒子利用更多的信息来决策自身的行为； 基于粒子维差异动态改变惯性权重，可有效避免算法陷入局部最优解，从而使算法有了新的突破. PC-DCWD算法实现过程如下：
步骤1： 初始化粒子群算法的相关参数，随机产生初始粒子.
步骤2： 计算初始种群中所有粒子的适应度值，并更新个体最优值和全局最优值.
步骤3： 计算种群的平均极值favr和当前迭代次数下所有粒子第d维位置的平均值pavrd. 对适应度f(Xi) > favr的劣等粒子，当pmd < pgd时，令惯性权重ω=ω1，否则ω = ω3，并按照式(10)来更新粒子速度； 对适应度f(Xi) ≤ favr的优等粒子，当pmd < pgd时，令惯性权重ω = ω2，否则ω = ω3，并按照式(11)来更新粒子速度； 计算所有粒子的适应度值，并更新个体最优值和全局最优值.
步骤4： 若满足迭代次数已达到最大或者达到所设定的阈值，则终止迭代过程； 否则，转至步骤3.
3.4 算法仿真测试与分析下面采用如表1所示的5个典型Benchmark测试函数来评价本文所提出的改进粒子群算法(PC-DCWD)，利用Matlab软件编写仿真程序，并与线性递减粒子群算法(LPSO)的测试结果进行比较.
| 函数名称 | 函数表达式 | 搜索范围 | 全局最优值 |
| Sphere | 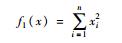 | [-100, 100] | f1(0，…，0)=0 |
| Rastrigrin | 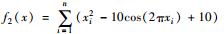 | [-10, 10] | f2(0，…，0)=0 |
| Rosenbrock | 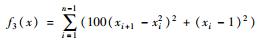 | [-5, 5] | f3(0，…，0)=0 |
| Griewank | 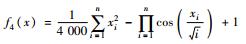 | [-100, 100] | f4(0，…，0)=0 |
| Ackley | 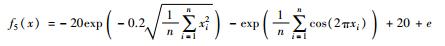 | [-30, 30] | f5(0，…，0)=0 |
为了准确比较算法的性能需要减少偶然性的影响，因此，对每个测试函数随机进行100次实验，且部分参数设置如下： 加速度常数c1=c2=2，惯性权重最小值ωmin=0.4，惯性权重最大值ωmax=0.9，最大迭代次数D=500，种群规模取40，维数取20维.
依据在100次实验中得到的全局最优值、平均最优值、得到最优解的成功率以及最优解的均方差4个方面的数据对算法的性能进行综合评估. 各函数比较结果如表2所示，对应的收敛寻优曲线如图3~7所示，其中横坐标为迭代次数，纵坐标为每一次迭代得到的平均适应度值.
| 函数名 | 算法 | 全局最优值 | 平均最优值 | 成功率/％ | 最优解均方差 |
| Sphere | LPSO | 0 | 3.804 1 | 40 | 0 |
| PC-DCWD | 0 | 0 | 100 | 0 | |
| Rastrigrin | LPSO | 0 | 23.985 6 | 18 | 0 |
| PC-DCWD | 0 | 0 | 100 | 0 | |
| Rosenbrock | LPSO | 18.004 8 | 381.951 1 | 0 | 0.781 33 |
| PC-DCWD | 1.394 1e-05 | 1.893 3 | 80 | 3.524 1e-05 | |
| Griewank | LPSO | 0 | 0.155 66 | 36 | 0 |
| PC-DCWD | 0 | 0 | 100 | 0 | |
| Ackley | LPSO | 8.881 8e-16 | 1.951 5 | 33 | 0 |
| PC-DCWD | 8.881 8e-16 | 8.881 8e-16 | 100 | 0 |
 |
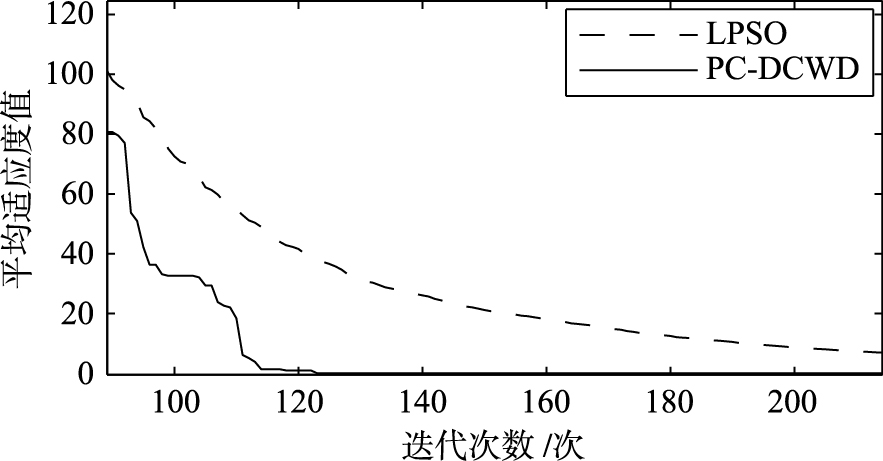| 图 3 Sphere函数的寻优曲线 Fig. 3 Optimization curves of Sphere function |
 |
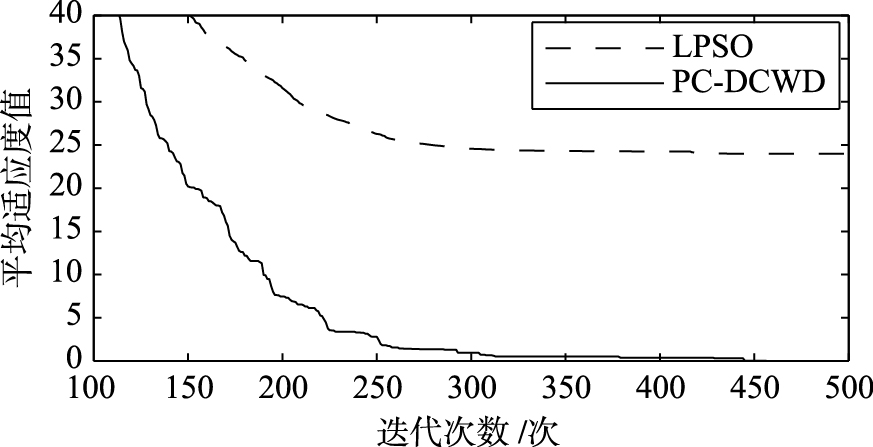| 图 4 Rastrigrin函数的寻优曲线 Fig. 4 Optimization curves of Rastrigrin function |
 |
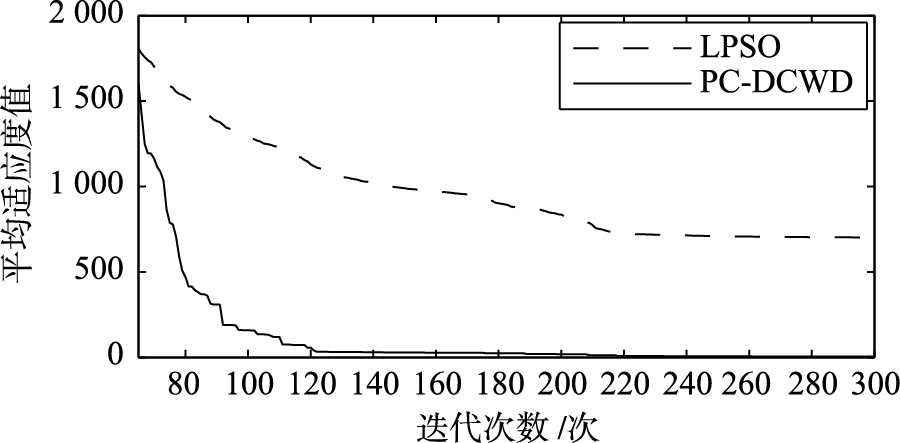| 图 5 Rosenbrock函数的寻优曲线 Fig. 5 Optimization curves of Rosenbrock function |
 |
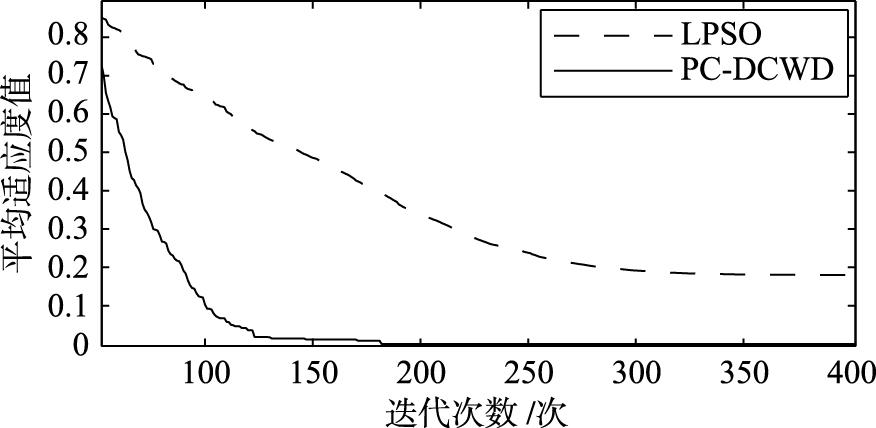| 图 6 Griewank函数的寻优曲线 Fig. 6 Optimization curves of Griewank function |
 |
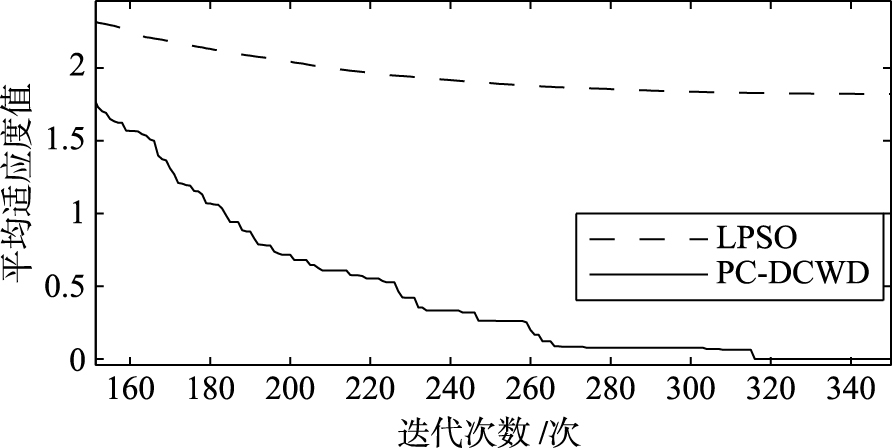| 图 7 Ackley函数的寻优曲线 Fig. 7 Optimization curves of Ackley function |
由表2知，在100次实验中，对于不同的测试函数，PC-DCWD算法找到的最优解基本上等于理论最优解，得到的适应度值也基本等于理论最优值. 其中Rosenbrock函数是很难极小化的病态函数，但由表中数据可知，PC-DCWD算法得到的最优值远优于LPSO得到的最优值，说明PC-DCWD算法具有更强的全局寻优能力. 除Rosenbrock函数外，PC-DCWD算法在每次实验中均能得到全局最小值，可见算法的稳定性也很好，收敛速度也较快； 而LPSO则效果很差. 以上结论也可从各函数的寻优曲线得到验证.
4 仿真实验 4.1 仿真条件设定由于所研究的Delta并联机械手物理样机及相关实验仪器正在筹备中，尚不能开展参数辨识实验. 因此，以下仅通过仿真实验验证上述改进粒子群算法在并联机械手参数辨识中的有效性. 具体实现如下：首先假定误差模型的9项误差均已知，根据采样点(Px，Py，Pz)可通过运动学逆解方程求得理想主动关节角度值θi. 又因为Δθi已知，因此3个主动关节角度真实值可由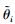=θi+Δθi得到. 而对于n个采样点，通过上述过程可以得到n组主动关节角度真实值. 然后，将9项误差设定值变为未知量进行标定. 相关参数设置如下： R=110 mm，r=75 mm，L=200 mm，K=520 mm，加速度常数c1=c2=2，惯性权重最小值ωmin=0.4，惯性权重最大值ωmax=0.9，最大迭代次数D=3 000，种群规模为50，维数取9维，实验运行50次. 为了对误差进行更充分的辨识，选取机械手操作端在平面Pz=-400和Pz=-600上的圆轨迹Px2+Py2=1002，将其离散化为两个圆上均匀分布的40个采样点，以式(7)为适应度函数进行参数辨识.
| 待辨识参数 | 真实值 /rad | 寻优范围 | LPSO辨识值 /rad | PC-DCWD辨识值 /rad |
| Δθ1 | 0.009 1 | [-1, 1] | 0.009 099 5 | 0.009 1 |
| Δθ2 | -0.023 1 | -0.023 101 | -0.023 1 | |
| Δθ3 | 0.027 5 | 0.027 5 | 0.027 5 | |
| Δα1 | 0.002 1 | 0.002 748 9 | 0.002 100 9 | |
| Δα2 | 0.020 1 | 0.019 508 | 0.020 1 | |
| Δα3 | 0.213 5 | 0.213 4 | 0.213 5 | |
| Δβ1 | 0.001 2 | 0.003 872 | 0.001 203 6 | |
| Δβ2 | 0.021 1 | 0.018 677 | 0.021 1 | |
| Δβ3 | 0.222 8 | 0.222 4 | 0.222 8 | |
| J | 8.151 8e-18 | 0.213 89 | 4.534 4e-07 | |
| 辨识值与真实值的均方差 | 0.001 244 9 | 1.240 6e-06 |
参数辨识寻优曲线如图8所示，仿真数据对比如表3所示，由表3可知，待辨识的参数真实值最大值0.222 8与绝对值最小值0.001 2相差近10-2的数量级，可见粒子群中粒子的各维具有较大差异、辨识结果表明，按照PC-DCWD算法几乎能准确找到全局最优解，其与真实值的均方差仅为1.240 6e-06，适应度函数值J几乎为0且收敛速度加快. 而LPSO算法由于未考虑粒子各维间的搜索差异，使得粒子的某维采用了过大或者过小的惯性权重进行位置更新，从而导致这一维跳出了最优解区域，使整个算法得到的最优解不准确. 由此可见，PC-DCWD算法具有更强的寻找全局最优解的能力.
 |
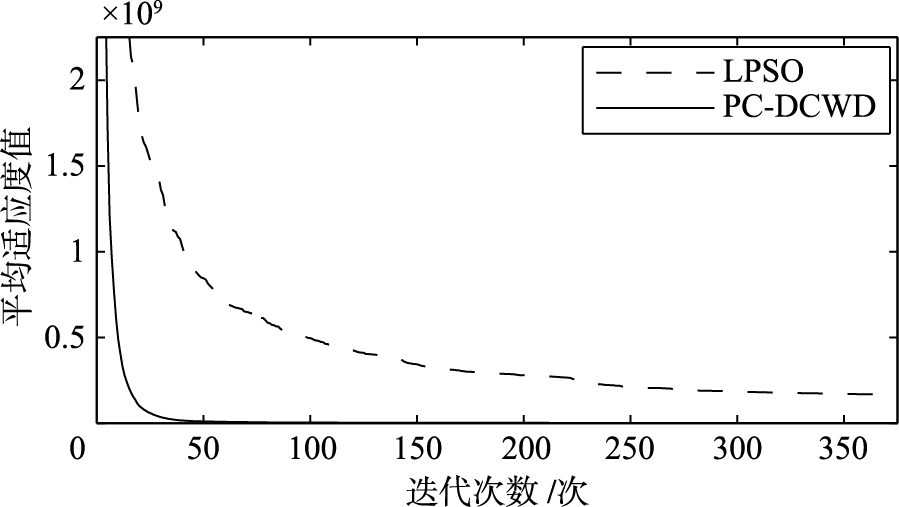| 图 8参数辨识寻优曲线 Fig. 8 Optimization curves of parameter identification |
本文选取对Delta并联机械手运动学精度影响比较大的9项主要误差源建立误差模型，利用一种改进的粒子群优化算法对其进行运动学参数辨识. 该算法引入平均极值对粒子进行分类，针对不同种类粒子采用异步进化策略，增强种群间的协作； 针对进化过程中同一个粒子的不同维度所出现的维差异问题，通过引入距离因子概念，实现粒子按维动态改变惯性权重的策略. 5个经典函数的测试结果显示，PC-DCWD算法能有效避免陷入局部最优，减轻了早熟收敛现象，收敛速度快，具有更强的全局寻优能力. 最后，通过对所建立的误差模型进行辨识，结果进一步验证该算法的有效性和可行性.
| [1] | 洪振宇, 梅江平, 赵学满, 等. 基于球杆仪检测信息的并联机构运动学标定[J]. 机械工程学报, 2007, 43(7): 16-22. Hong Z Y, Mei J P, Zhao X M, et al. Kinematic calibration of the parallel mechanism using double-ball-bar system[J]. Chinese Journal of Mechanical Engineering, 2007, 43(7): 16-22. |
| [2] | 张立杰, 李永泉, 王艮川. 基于三坐标测量机的球面5R并联机构运动学标定研究[J]. 中国机械工程, 2013, 24(22): 2997-3002. Zhang L J, Li Y Q, Wang G C. Research on kinematic calibration of spherical 5R parallel manipulator based on coordinate measuring machine[J]. China Mechanical Engineering, 2013, 24(22): 2997-3002. |
| [3] | 张文昌, 梅江平, 刘艺, 等. 基于激光跟踪仪的Delta并联机构运动学误差标定[J]. 天津大学学报, 2013, 46(3): 257-262. Zhang W C, Mei J P, Liu Y, et al. Calibration of Delta parallel robot kinematic errors based on laser tracker[J]. Journal of Tianjin University, 2013, 46(3): 257-262. |
| [4] | 潘伯钊, 宋轶民, 王攀峰, 等. 基于激光跟踪仪的混联机器人快速零点标定方法[J]. 机械工程学报, 2014, 50(1): 31-37. Pan B Z, Song Y M, Wang P F, et al. Laser tracker based rapid home position calibration of a hybrid robot[J]. Chinese Journal of Mechanical Engineering, 2014, 50(1): 31-37. |
| [5] | 孙月海, 王兰, 梅江平, 等. 基于单目视觉的Delta机器人零点标定方法[J]. 天津大学学报, 2013, 46(3): 239-243. Sun Y H, Wang L, Mei J P, et al. Zero calibration of Delta robot based on monocular vision[J]. Journal of Tianjin University, 2013, 46(3): 239-243. |
| [6] | Alberto T, María S J, Eduardo C, et al. One camera in hand for kinematic calibration of a parallel robot[C] //Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway, NJ, USA: IEEE, 2010: 5673-5678. |
| [7] | Antonelli G, Chiaverini S, Fusco G. A calibration method for odometry of mobile robots based on the least-squares technique: Theory and experimental validation[J]. IEEE Transactions on Robotics, 2005, 21(5): 994-1004. |
| [8] | Grotjahn M, Daemi M, Heimann B. Friction and rigid body identification of robot dynamics[J]. International Journal of Solids and Structures. 2001, 38(10/11/12/13): 1889-1902. |
| [9] | 韩江义, 游有鹏, 虞启凯. Delta并联机构正向运动学标定方法研究[J]. 农业机械学报, 2013, 44(6): 253-257. Han J Y, You Y P, Yu Q K. Forward kinematic calibration of Delta parallel mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(6): 253-257. |
| [10] | 冯春时. 群智能优化算法及其应用[D]. 合肥: 中国科学技术大学, 2009. Feng C S. Swarm intelligence optimization algorithms and their applications[D]. Hefei: University of Science and Technology of China, 2009. |
| [11] | Kennedy J, Eberhart R. Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks. Piscataway, NJ, USA: IEEE, 1995: 1942-1948. |
| [12] | Shi Y H, Eberhart R. A modified particle swarm optimizer[C]//Proceedings of the IEEE Congress on Computational Intelligence. Piscataway, NJ, USA: IEEE, 1998: 69-73. |
| [13] | Shi Y, Eberhart R C. Empirical study of particle swarm optimization[C]//Proceedings of the IEEE Congress on Evolutionary Computation. Piscataway, NJ, USA: IEEE, 1999: 1945-1950. |
| [14] | Chatterjee A, Siarry P. Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization[J]. Computers and Operations Research, 2006, 33(3): 859-871. |
| [15] | 张顶学, 关治洪, 刘新芝. 一种动态改变惯性权重的自适应粒子群算法[J]. 控制与决策, 2008, 23(11): 1253-1257. Zhang D X, Guan Z H, Liu X Z. Adaptive particle swarm optimization algorithm with dynamically changing inertia weight[J]. Control and Decision, 2008, 23(11): 1253-1257. |
| [16] | 张朝龙, 江巨浪, 江善和, 等. 一种自适应混合粒子群优化算法及其应用[J]. 计算机应用研究, 2011, 28(5): 1696-1698. Zhang Z L, Jiang J L, Jiang S H, et al. Adaptive hybrid particle swarm optimization algorithm and application[J]. Application Research of Computers, 2011, 28(5): 1696-1698. |
| [17] | 陈国强, 李旻, 张新刚. 基于局部搜索惯性权重的粒子群优化算法[J]. 计算机应用研究, 2011, 28(3): 857-858, 908. Chen G Q, Li M, Zhang X G. Particle swarm optimization algorithm based on local search for inertia weight[J]. Application Research of Computers, 2011, 28(3): 857-858, 908. |
| [18] | 高哲, 廖晓钟. 基于平均速度的混合自适应粒子群算法[J]. 控制与决策, 2012, 27(1): 152-155. Gao Z, Liao X Z. Hybrid adaptive particle swarm optimization based on average velocity[J]. Control and Decision, 2012, 27(1): 152-155. |
| [19] | 杜继永, 张凤鸣, 李建文, 等. 一种具有初始化功能的自适应惯性权重粒子群算法[J]. 信息与控制, 2012, 41(2): 165-169. Du J Y, Zhang F M, Li J W, et al. A particle swarm optimization algorithm with initialized adaptive inertia weights[J]. Information and Control, 2012, 41(2): 165-169. |
| [20] | 张迅, 王平, 邢建春, 等. 基于高斯函数递减惯性权重的粒子群优化算法[J]. 计算机应用研究, 2012, 29(10): 3710-3712, 3724. Zhang X, Wang P, Xing J C, et al. Particle swarm optimization algorithms with decreasing inertia weight based on Gaussian function[J]. Application Research of Computers, 2012, 29(10): 3710-3712, 3724. |