2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
1 引言
随着全球消化道疾病患者的不断增加,胶囊内窥镜已经成为继常规消化道内窥镜之后又一广泛用于临床的消化道检查手段. 自2001年以色列GIVEN公司研发的“M2A”胶囊内窥镜[1]进入临床使用以来,胶囊内窥镜因其可实现全消化道无痛苦检查并能严格控制交叉感染的优点,得到了医护人员和患者的广泛认可. 然而,胶囊内窥镜是依靠小肠蠕动实现运动,这种被动的运动方式不但耗费大量时间,而且存在漏检的可能,甚至会引发肠梗阻的危险. 因此,近十多年来国内外许多研究小组致力于研发可以自主运动的胶囊机器人,并取得了多项成果.
已见报道的自主运动的胶囊机器人,可按驱动器的设计分为两大类:内部激励驱动方式和外磁驱动方式. 内部激励驱动方式中最具有代表性的是仿生驱动和多足驱动. 韩国科学技术院[2]、 上海交通大学[3]及香港中文大学[4]等应用该驱动方式设计了原理样机,但此种类型的胶囊机器人大多结构复杂、 体积较大、 能耗较高并可能对小肠壁造成损伤,目前这类研究尚停留在实验室阶段. 多足驱动胶囊机器人依靠一系列微型足运动,意大利CRIM实验室的Dario最早研制了多足驱动胶囊机器人[5],随后韩国延世大学的Kim也进行了相关研究[6],但其应用倒钩抓附器官的方式容易导致肠道、 尤其是病变部位的损伤而引起感染,存在安全隐患. 此外内部激励驱动方式还包括螺旋驱动[7]、 电刺激驱动[8]等. 外磁驱动方式是依靠外部的磁场发生器产生全方向的磁场,通过改变外部磁场控制胶囊运动. 日本东北大学Sendoh通过改变外部磁场方向使得胶囊在体内产生旋转,利用胶囊表面螺纹与肠道黏液产生的推力前进[9],国内的大连理工大学[10]和深圳先进技术研究院[11]也对此磁致旋转驱动方式进行了研究并研制了样机. 意大利比萨大学的Carpi用磁性外壳包裹现有的被动式胶囊内镜,利用外部磁场直接驱动胶囊运动[12],华中科技大学采用了这种驱动方式[13]. 外磁驱动方式效率高,突破了驱动耗能过大的瓶颈,德国西门子医疗和日本奥林巴斯医疗系统已宣布合作开发磁导航胶囊内窥镜[14],但目前胶囊定位技术并不成熟,多依赖X光扫描,并且检查过程中患者须长时间平躺在磁场范围内,因此该驱动方式距进入临床应用尚有一定距离. 此外,研究人员还尝试将上述两类驱动混合应用以求得更好的运动效果[15, 16, 17],但目前也只停留在实验室样机阶段.
目前在研的胶囊机器人,以外磁驱动胶囊和内置冲击式驱动器的“内力—摩擦”胶囊在外形上与已投入临床使用的被动式胶囊内窥镜最为接近,因此,研究这一类胶囊机器人在肠道内工作的运动特点,有着现实的工程意义. 目前,在这方面已有的研究,偏重探讨胶囊本体与肠道之间的交互摩擦特性及阻力大小[18, 19],而对胶囊在肠道内的启动过程却关注甚少[20],更缺乏对胶囊与肠道间力交互的量化动力学分析.
本文针对和被动式胶囊内窥镜外形相似的一类胶囊机器人,包括外磁驱动和内置驱动器的“内力—摩擦”式机器人,拟通过建立小肠与肠壁组织交互过程的动力学方程,刻画其从静止到克服临界摩擦力发生滑移这一段过程的速度—位移状态的变化,进而解释胶囊机器人驱动力的给力方式与运动状态的变化关系,为后续的研究提供理论依据.
2 “内力—摩擦”胶囊机器人驱动原理及结构本研究的工作基础是“内力—摩擦”式胶囊机器人,其驱动器的结构设计源于音圈电机基本原理.
2.1 “内力—摩擦”式驱动原理“内力—摩擦”式驱动原理利用内部滑块与外壳之间的相互作用力及外壳与外部环境的静摩擦力实现胶囊机器人单自由度运动. 其驱动原理如图1所示,运动过程包括4个阶段.
 |
| 图 1 “内力—摩擦”式胶囊机器人1周期内的运动步骤 Fig. 1 The motion steps of the “inner force-friction” capsubot during a single period |
阶段1:滑块受较大的力快速向后(图中向左)运动,同时外壳受到向前的反作用力,该力大于外壳与接触面的摩擦力,外壳获得向前的加速度而前进.
阶段2:改变内力的方向,滑块受到向前的作用力,速度逐渐减小到零,外壳受到与其相反的作用力,速度也逐渐减小到零.
阶段3:滑块继续受到向前的较小的内力而缓慢运动,由于此时内力小于环境的最大静摩擦力,因而外壳能够保持静止状态.
阶段4:滑块受到向后的较小的内力,速度逐渐减小到零,外壳一直保持静止状态,完成一个运动周期.
基于上述驱动原理,胶囊机器人的运动可表示为
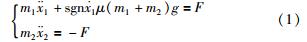
其中,m1、 m2分别为外壳和内部滑块的质量,x1、 x2分别为外壳和内部滑块的绝对位移,μ为外壳与外界的滑动摩擦系数,F为外壳与内部滑块间的交互作用力. 由前期工作可知,在同等的功率消耗下,将输出力向行程的两端集中时,将获得较好的运动效果. 根据“内力—摩擦”驱动原理,增大滑块与外壳之间的质量比、 内力与摩擦力比,将会分别增加机器人运行的步长和频率,提高运行速度.
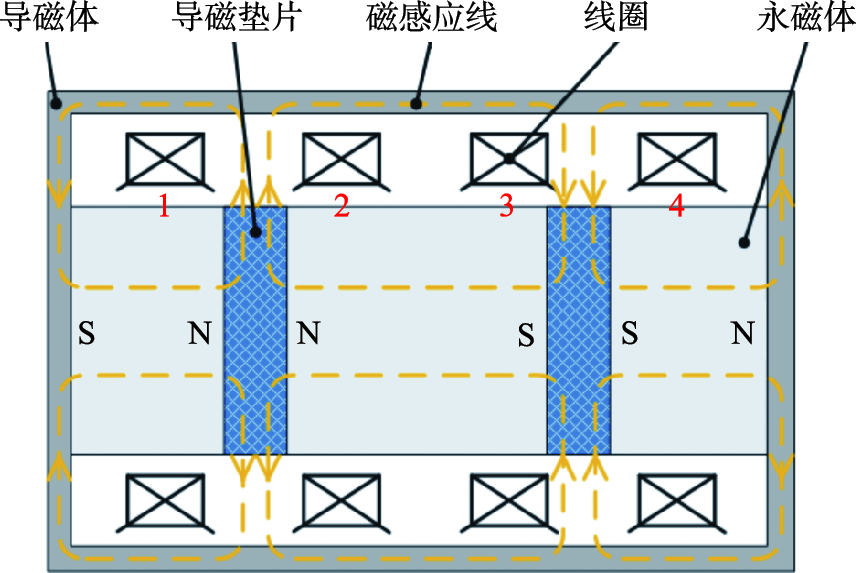
2.2 “内力—摩擦”式胶囊机器人驱动器结构胶囊机器人驱动器结构的设计可以和传统音圈电机类比. 音圈电机属于动圈式直线振荡电机,它以轻质量的线圈为动子,便于实现较高的振动频率; “内力—摩擦”式胶囊机器人需要的驱动器特性正好与其相反,要求动子具有较大的惯性,因此,驱动器的线圈作为定子与外壳相连,而其它较大质量的部分作为动子,以最大限度增加动子与定子的质量比. 加大磁通密度可有效提高输出力,对于音圈电机的结构,工作气隙的磁通密度增高时,端部和非工作气隙部分的磁漏将严重的影响永磁体的利用率,因此采用多个基本的音圈电机结构串联,其中永磁体的布置方式及产生的磁路如图2所示.
 |
| 图 2 “内力—摩擦”式胶囊驱动器结构简图 Fig. 2Constructional diagram of the driver of the “inner force-friction”capsubot |
该方法基本消除了永磁体圆柱侧面以外的漏磁,并且使得磁通在导磁垫片外侧的工作气隙中产生聚磁效果,得到了较理想的效果,并且采用多组线圈分时供电的方法避免了线圈在磁通密度较低位置时的能量损耗.
在图2中,作为定子的4个线圈之间的相对位置关系固定,所有其它部分作为动子. 驱动器工作过程为:初始时动子位于最右端,此时线圈2和线圈4将分别位于两块导磁垫片的外侧气隙. 控制线圈2和线圈4的电流方向,使定子均受到向左的电磁力而滑动. 当垫片刚刚滑出线圈2、 4的位置时,改由给线圈1、 3供给特定方向的电流,使定子继续向左滑动,直到达到行程的最左端. 接下来按照先线圈1、 3后线圈2、 4的顺序供给相反方向的电流时,动子返回初始位置,完成一个运动周期. 由于永磁体圆柱侧面存在漏磁现象,因此当线圈完全处于垫片外侧气隙区域时,仍然存在电磁力,整个行程能够顺利完成.
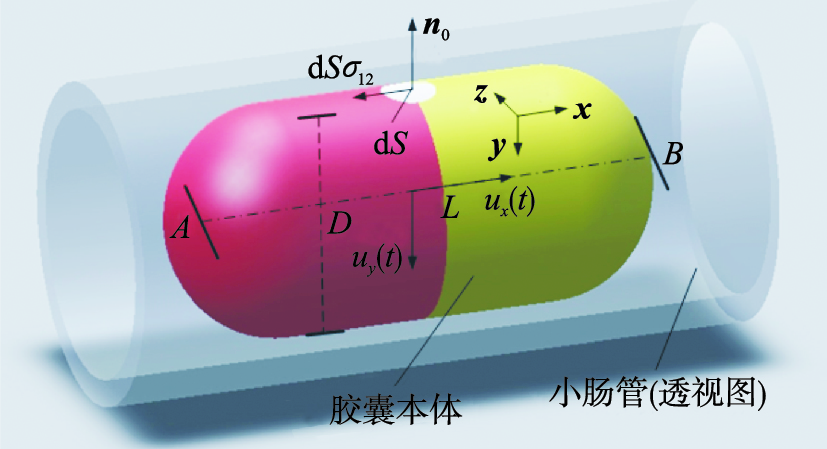
3 动力学分析图3为胶囊机器人在肠道中运动时的透视图. 顶部白色区域dS表示胶囊外壳与肠管内壁的接触面元,n0是垂直于dS的单位矢量. 胶囊外壳与肠道内壁之间存在剪切力,在x方向上,该力为dSσxy,其中σxy为应力张量σ在x方向上的分量. D为胶囊柱形本体的直径(6.5 mm),线段AB表示胶囊通体身长(33 mm). ux和uy分别是作用在胶囊上的外驱动力u(t)在x和y方向上的分量,也是关于时间的函数. 胶囊机器人启动后,将迫使小肠管沿着其运动方向发生剪切形变.
 |
| 图 3 胶囊机器人在小肠内受力的3维分析 Fig. 3 The 3D analysis of the mechanical condition for the capsubot inside the intestine |
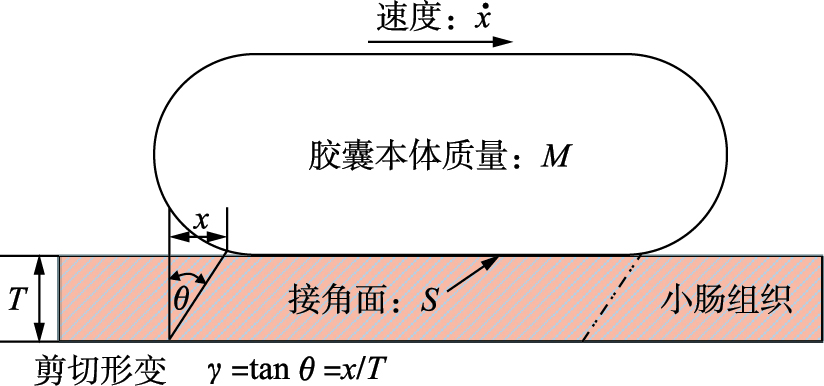
如图4所示,小肠组织的厚度为T,x是胶囊外壳与小肠壁的接触面S上一点的位移. 胶囊机器人本体的质量为M. 由工程剪切应变的定义:

 |
| 图 4 胶囊机器人的启动引起小肠组织的剪切形变 Fig. 4 The shear deformation of the intestinal tissue caused by the start of the capsubot |
为简化分析,这里不考虑剪切形变时肠壁厚度的微小变化,将该剪切运动视为简单剪切. 因此,相应的形变梯度张量F与水平位移x的关系为

相应的,计算得到左柯西—格林张量为
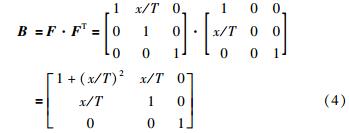
首先假设小肠组织的剪切弹性模量为常数G,考察应力应变满足线弹性关系时的情况. 小肠组织满足各项同性及不可压缩的条件,σxy=σyx=GBxy及拉压弹性模量E≈3G,有σkk=3GBkk,k=1,2,3.
由本构关系为线弹性这一前提,将其中的主轴应变和剪应变表示为关于接触位移x的式子,得到:
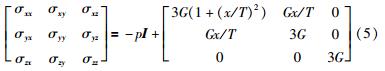
胶囊运动的动力学方程是:
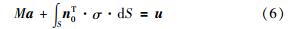
其中M为胶囊的质量,a是其运动加速度. 将其写成3维形式,得到式(7):

由于胶囊外壳与肠壁的接触面关于肠管轴对称且在该接触面上的剪切应力处处相等,因此将式(7)沿整个接触面S作积分之后,y方向上所受合力为0,仅余x方向上的受力关系为式(8):
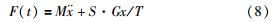
事实上,小肠组织的剪切模量G并不是一个常数,而是时间的函数. 因此,由五元件线性粘弹性模型:
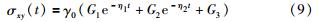
可知,剪切模量为
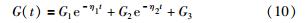
为了在速度—位移相平面上观察胶囊受到外力后的运动情况,根据式(8),推导状态方程:
令x,x2= ,记X=[x1,x2]T. 该状态包含了胶囊的位移和速度信息,因而:
,记X=[x1,x2]T. 该状态包含了胶囊的位移和速度信息,因而:
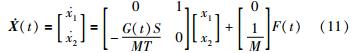
式(11)又可对应写作:
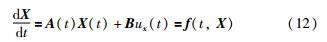
此即状态量在速度—位移相平面上的变化速度矢量. 由式(11)可知,要计算某一时刻该矢量的值,需要知道当前胶囊的位移、 速度及作用于胶囊上的驱动力的施加方式,如若施加给胶囊的外力为类似于方波的“脉冲”,则该力的“脉冲”的幅值与持续时间都会影响计算结果. 进一步地,可画出相平面图,并据此观察和量化分析驱动力的施加方式启动胶囊运动状态的过程.
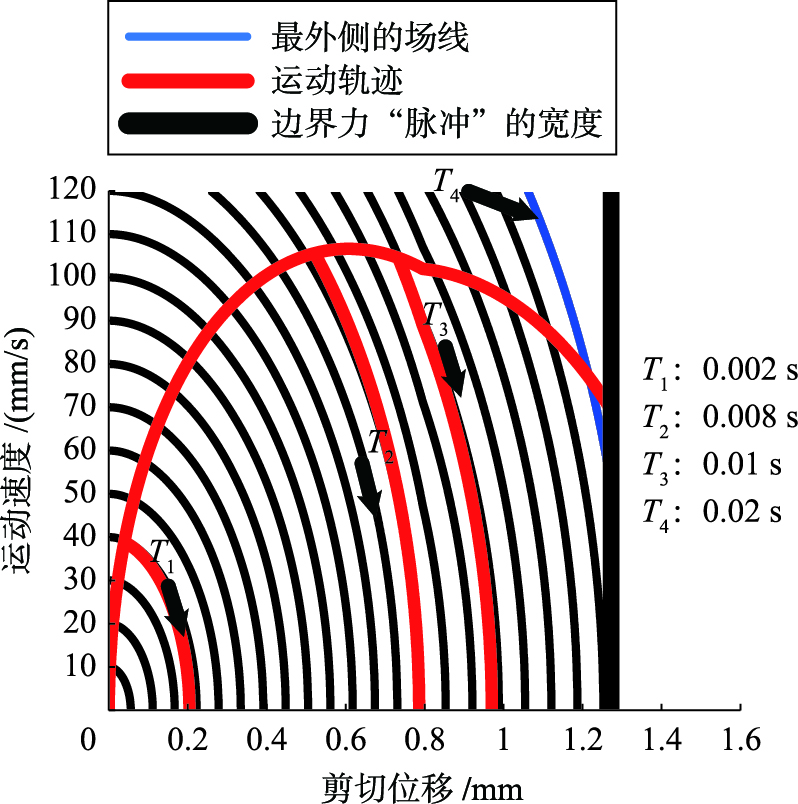
4 计算结果图5中4条轨迹T1~T4代表胶囊受到不同的力的“脉冲”后,从静止状态加速的过程. 驱动力的幅值为0.2 N,从T1到T4给力的时间宽度分别为0.002 s、 0.008 s、 0.01 s和0.02 s. 其中的背景弧线为该速度—位移向量场的场线(零输入响应),它与纵轴的交点代表胶囊在受到某个力的冲量后将“瞬间”达到相应的初速度,与横坐标的交点代表胶囊速度衰减为零时最远能到达的位移处,过程中不再有外力输入.
 |
| 图 5 胶囊机器人的启动过程在“速度—位移”相平面上的反映 Fig. 5 The observation for the startup process of the capsubot on the “velocity-displacement” phase |
胶囊在肠道中受力后的运动状态,对应于相平面上从原点出发穿过这些场线的运动轨迹; 胶囊状态所在的场线越远离原点,意味着到达该点需要做的功越多. 因此,驱动力越大,轨迹越容易穿过更多的场线; 同样的驱动力,若力的持续时间不足,则运动轨迹会从中途“跌落”,这是因为胶囊运动到中途时不再有外力输入,其动能不再增大.
该结果的绘制采用了式(12)的迭代形式. 为提高精度,采用4阶龙格库塔公式:
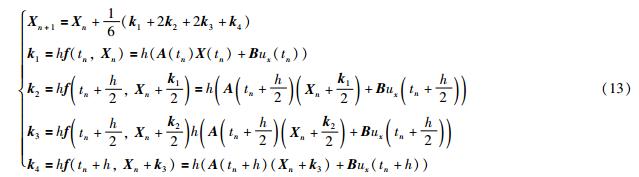
取胶囊与小肠内壁接触面上的压强P=29.209 kPa,摩擦系数μ=0.003. 压强数值的具体计算过程和胶囊的外部形状和尺寸有关[21],最大的摩擦阻力为fmax=μPS=71 mN,小于这里给出的驱动力. 表1反映了式(9)中的5个参数G1、 G2、 G3及η1和η2随剪切应变的幅值变化而相应发生改变的现象. 表中数据来自前期工作[22](参见文[22]的应力松弛实验),并在文[22]的工作基础上作了修正.
| G1/Pa | G2/Pa | G3/Pa | η1 | η2 | |
| 20% | 477.4 | 192.1 | 331.7 | 11.61 | 0.314 4 |
| 50% | 559.6 | 150.2 | 235.1 | 15.15 | 0.300 0 |
| 80% | 436.5 | 130.2 | 202.5 | 13.50 | 0.265 6 |
| 100% | 345.5 | 114.0 | 187.6 | 11.97 | 0.225 1 |
图5右侧的竖线表示速度—位移向量场的边界. 在该边界右侧,由于胶囊外壳与小肠内壁已经脱离接触,因此式(11)不再成立. 边界的确定是依据不等式(14):

这是因为随着胶囊的运动,同时肠壁发生形变,肠壁与胶囊外壳之间的摩擦力逐渐增大. 当该摩擦力增大到不足以维持形变时,滑移产生. 通过迭代计算,跟踪胶囊的状态X(t)和摩擦力f:

式(14)是式(15)迭代过程的结束条件. 当迭代结束时,记录下该时刻的胶囊状态,确定滑移临界点.
由图5可知,在上文探讨的4种驱动力方案中,若确定驱动力为0.2 N,只有当脉冲宽度达到0.02 s以上时,胶囊才具备在肠道中运动的能力,在图上表现为运动轨迹突破最外面的一条场线.
这里,设定时间步长h=2 μs. 小肠厚度T=1 591 μm,胶囊质量M=10 g,接触面S=πDL(L=AB-D为胶囊中段的长度).
5 总结本文以一类在外形上和被动式胶囊内窥镜相似的胶囊机器人(外磁驱动式和“内力—摩擦”式)的研究为工程背景,对胶囊机器人和肠道力交互过程中的力学问题进行了分析研究. 根据连续介质力学的理论,建立了胶囊运动的动力学方程. 基于课题组前期工作测得的五元件粘弹性模型实验数据,计算并绘制了胶囊运动的速度—位移相平面图,并量化显示了外驱动力脉冲的宽度对胶囊启动运动轨迹的影响. 本文提供的分析方法有助于优化设计胶囊机器人驱动力的给力方式,以期用较少的能量输入达到成功驱动的效果.
| [1] | Iddan G, Meron G, Glukhovsky A, et al. Wireless capsule endoscopy[J]. Nature, 2000, 405(6785): 417. |
| [2] | Kim B, Park S, Jee C Y, et al. An earthworm-like locomotive mechanism for capsule endoscopes[C]//2005 IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, NJ, USA: IEEE, 2005: 2997-3002. |
| [3] | 李传国, 颜国正, 王坤东, 等. 主动可控内窥镜胶囊机器人研究[J]. 测控技术, 2010, 29(4): 90-93. Li C G, Yan G Z, Wang K D, et al. Development of micro-robot for the active exploration of the gastrointestinal track[J]. Measurement and Control Technology, 2010, 29(4): 90-93. |
| [4] | Wang X, Meng M Q H. An inchworm-like locomotion mechanism based on magnetic actuator for active capsule endoscope[C]//2006 IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, NJ, USA: IEEE, 2006: 1267-1272. |
| [5] | Quaglia C, Buselli E, Iii R J W, et al. An endoscopic capsule robot: A meso-scale engineering case study[J]. Journal of Micromechanics and Microengineering, 2009, 19(10): 466-467. |
| [6] | Kim H M, Yang S, Kim J, et al. Active locomotion of a paddling-based capsule endoscope in an in vitro and in vivo experiment (with videos)[J]. Gastrointestinal Endoscopy, 2010, 72(2): 381-387. |
| [7] | 周银生, 李立新, 赵东福. 一种新型的微型机器人[J]. 机械工程学报, 2001, 37(1): 11-13. Zhou Y S, Li L X, Zhao D F. New kind of micro-robot[J]. Chinese Journal of Mechanical Engineering, 2001, 37(1): 11-13. |
| [8] | Rark H J, Lee J H, Moon Y K, et al. New method of moving control for wireless endoscopic capsule using electrical stimuli[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2005, 88(6): 1476-1480. |
| [9] | Sendoh M, Ishiyama K, Arai K I. Fabrication of magnetic actuator for use in a capsule endoscope[J]. IEEE Transactions on Magnetics, 2003, 39(5): 3232-3234. |
| [10] | 张永顺, 于宏海, 阮晓燕, 等. 新型肠道胶囊式微型机器人的运动特性[J]. 机械工程学报, 2009, 45(8): 18-23. Zhang Y S, Yu H H, Ruan X Y, et al. Kinematics characteristics of a new capsule-type micro robot in intestine[J]. Chinese Journal of Mechanical Engineering, 2009, 45(8): 18-23. |
| [11] | Yang W, Hu C, Meng M Q H. A new 6D magnetic localization technique for wireless capsule endoscope based on a rectangle magnet[J]. IEEE Transactions on Magnetics, 2009(2): 360-364. |
| [12] | Carpi F, Pappone C. Magnetic maneuvering of endoscopic capsules by means of a robotic navigation system[J]. IEEE Transactions on Biomedical Engineering, 2009, 56(5): 1482-1490. |
| [13] | Gao M, Hu C, Chen Z, et al. Design and fabrication of a magnetic propulsion system for self-propelled capsule endoscope[J]. IEEE Transactions on Biomedical Engineering, 2010, 57(12): 2891-2902. |
| [14] | Rey J F, Ogata H, Hosoe N, et al. Blinded nonrandomized comparative study of gastric examination with a magnetically guided capsule endoscope and standard videoendoscope[J]. Gastrointestinal Endoscopy, 2012, 75(2): 373-381. |
| [15] | Yim S, Jeona D. Capsular microrobot using directional friction spiral[C]//IEEE International Conference on Robotics and Automation. Piscataway, NJ, USA: IEEE, 2009: 4444-4449. |
| [16] | Simi M, Valdastri P, Quaglia C, et al. Design, fabrication, and testing of a capsule with hybrid locomotion for gastrointestinal tract exploration[J]. IEEE/ASME Transactions on Mechatronics, 2010, 15(2): 170-180. |
| [17] | Wang X, Meng M Q H, Chen X. A locomotion mechanism with external magnetic guidance for active capsule endoscope[C] //2010 Annual International Conference of the IEEE Engineering in Medicine and Biology Society.Piscataway, NJ, USA: IEEE, 2010: 4375-4378. |
| [18] | Li H, Furuta K, Chernousko F L. Motion generation of the capsubot using internal force and static friction[C]//45th IEEE Conference on Decision and Control. Piscataway, NJ, USA: IEEE, 2006: 6575-6580. |
| [19] | Zhang C, Liu H, Tan R, et al. Modeling of velocity-dependent frictional resistance of a capsule robot inside an intestine[J]. Tribology Letters, 2012, 47(2): 295-301. |
| [20] | Zhang C, Liu H, Li H. Experimental investigation of intestinal frictional resistance in the starting process of the capsule robot[J]. Tribology International, 2014, 70: 11-17. |
| [21] | 谭人嘉, 刘浩, 李洪谊, 等. 胶囊机器人与肠道准静态交互的临界滑动阻力研究[J].机器人, 2014, 36(6): 704-710. Tan R J, Liu H, Li H Y, et al. Research on the critical sliding resistance on the quasi-static interaction between the capsule robot and the small intestine[J]. Robot, 2014, 36(6): 704-710. |
| [22] | Tan R, Liu H, Su G, et al. Experimental investigation of the small intestine's viscoelasticity for the motion of capsule robot[C]//2011 International Conference on Mechatronics and Automation. Piscataway, NJ, USA: IEEE, 2011: 249-253. |



