2. 中国科学院大学, 北京 100049;
3. 华晨汽车工程研究院, 辽宁沈阳 110027
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Brilliance Automobile Engineering Research Institute, Shenyang 110027, China
1 引言
多传感器测量与感知系统是集目标测量、数据处理和信息融合利用于一体的多层次、多粒度复杂信息处理系统,在工业系统监测[1, 2]、故障诊断[3]、空间定位[4, 5]、环境观测[6, 7]等诸多领域得到大量应用. 其中在数据层,面向同源同构多传感器感知序列融合问题是多传感器数据融合中的重要内容之一[8]. 由多个相同传感器构成的感知系统对同一测量目标的某一个参数进行测量,既能够避免单个传感器系统由于系统故障所造成的测量失效或失真,也有助于提高测量的准确性. 但在实际应用中,多个同类感知节点的测量结果受到传感器装置本身性能参数差异和外界干扰的双重影响,具有较大的不确定性[9]; 另外,感知节点有限的计算能力与实时在线分析的需求客观上限制了传统融合方法的有效应用. 因此,针对同源同构感知序列融合问题开发一种计算简单、能够在线应用且具有较高的适应性和融合精度的数据融合计算方法具有很强的现实意义和实用价值.
传统的针对同源同类型多传感器感知序列融合方法很多,概括起来主要有加权平均[9, 10, 11]、贝叶斯估计[12, 13]、最大似然估计[14]、卡尔曼滤波[15]、神经元网络[16]、模糊逻辑[17, 18]等方法. 其中,加权平均法特别适用于同源同构多传感器在数据层的融合,但权重的分配对融合效果的影响十分明显[11]; 贝叶斯估计、最大似然估计等基于统计的方法需要了解目标对象的统计先验知识; 卡尔曼滤波方法要求知道系统的数学模型和噪声统计特性[15],且无法处理新增传感器的问题; 基于神经元网络的融合方法需要训练和学习过程,运算量随着输入维数和隐层神经元个数的增加而增长,且同样不适用于输入源发生变化的情况; 基于模糊C均值(FCM)聚类的融合方法[19]直接对同源同类多传感器数据进行融合处理,具有计算简单、无先验知识和系统模型限制、可在线应用等优点,但融合结果依赖于聚类个数确定的是否准确.
基于以上分析,本文针对未知目标感知测量中无先验、无系统模型条件下的同源同构多传感器感知序列在线融合计算问题,提出一种基于改进模糊聚类的在线融合方法. 该方法避免了传统模糊聚类融合方法中对聚类数设定的依赖,能够有效去除偏移较大的数据源和异常信号对融合结果的不良影响; 同时通过历史融合结果对当前融合的指导,进一步提高了融合的稳定性和精确性. 仿真实验表明,该方法较传统自适应加权平均和聚类融合方法有更好的融合精度和鲁棒性. 同时,由于该方法具有计算简单、可在线应用、不受传感器数目限制等优点,因此具有较好的适应性和实用价值.
2 融合机理分析传感器装置在测量中所产生的误差主要包括系统误差、随机误差和粗大误差三大类[20]. 设Zi(t)为t时刻系统观测值, (t)为被测参数真实值,
(t)为被测参数真实值, i(t)为传感器i的测量真值,则有:
i(t)为传感器i的测量真值,则有:
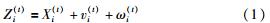

其中,vi(t)为系统误差,通常表现为测量值较真实值在某一方向上存在的规律性偏移; ni(t)为随机误差,通常服从某种统计规律; ωi(t)为粗大误差,具有较大的偶发性. 这里假设系统随机误差服从零均值正态分布,即ni(t)~N(0,σi2),则对于多个同类传感器对同一目标进行测量而言,可近似认为各观测值Zi(t)~N(0,σi2). 在实际测量中,不同传感器观测值Z(t)={Z1(t),Z2(t),…,Zm(t)}的分布情况可由图1所示.
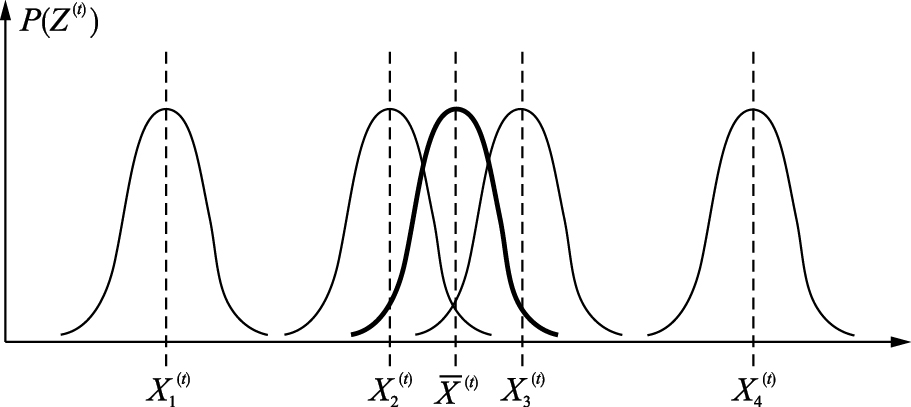 |
| 图 1 同构多传感器观测值分布示意图 Fig. 1 Observation distribution map of the homogeneous multi-sensors |
从图1可以看出,在保证有效测量的前提下,通常绝大多数Xi(t)“聚集”在以 (t)为中心、距离
(t)为中心、距离 (t)较近的区域,即绝大多数的vi(t)→0; 仅有少数的传感器由于故障等原因,使得|vi(t)| > ε.
(t)较近的区域,即绝大多数的vi(t)→0; 仅有少数的传感器由于故障等原因,使得|vi(t)| > ε.
基于上述假设,给出融合思路如下: 对t时刻各个传感器的观测值进行模糊聚类处理,其中距离 (t)较近的绝大多数观测值被归为一类并进行融合处理; 距离
(t)较近的绝大多数观测值被归为一类并进行融合处理; 距离 (t)较远的观测值被认为是异常测量值而归为异常值不参与融合计算. 通过上述措施,有效地避免了远离真值的观测值对融合结果的不良影响.
(t)较远的观测值被认为是异常测量值而归为异常值不参与融合计算. 通过上述措施,有效地避免了远离真值的观测值对融合结果的不良影响.
本文所提基于改进模糊聚类数据融合方法整体融合架构如图2所示. 被测目标系某一个属性参数经多个传感器感知测量形成多个观测值(Z1(t)~Zm(t)). 各当前观测值与历史数据、历史融合结果等数据经过统计权值计算后,形成基于统计权值的影响因子λi(t). 利用改进的模糊聚类方法对各传感源的观测值和计算后的影响因子进行模糊聚类计算,得到融合结果. 融合结果反馈到下一时刻融合过程中影响因子计算过程.
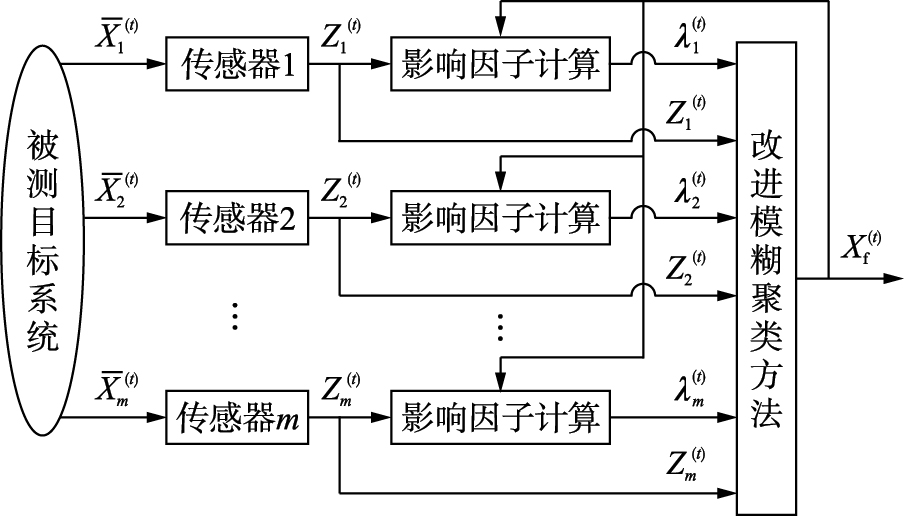 |
| 图 2 基于改进模糊聚类数据融合方法融合架构 Fig. 2 Structure of the data fusion method based on advanced fuzzy clustering |
传统的同源同构多传感器数据融合方法均针对当前时刻的多源数据集进行分析[19]. 但在实际融合过程中,历史数据与历史融合结果之间的关系能够在很大程度上反映各个传感源观测值与融合结果之间差异大小及分布情况. 考虑到这些规律对于下一时刻的融合有着一定的指导作用,因此引入基于历史数据和历史融合结果的统计权值λ.
设ZiL={Zi(t-1),Zi(t-2),…,Zi(t-L)}为t时刻前L时刻的历史观测值集合; XfL={Xf(t-1),Xf(t-2),…,Xf(t-L)}为t时刻前L时刻融合结果集合. 各传感器融合方差计算公式如下:
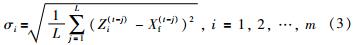
迭代计算公式如下:
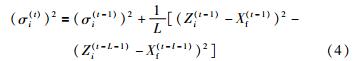
各传感器统计权值λi(t)的计算公式:
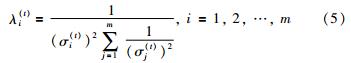
RFCM是一种由传统FCM基础上,通过引入噪声类改良而来的聚类方法[21]. 设X={x1,x2,…,xn}为S维空间中n个任意给定数据集合,xk(k=1,2,…,n)为样本点; P={C1,C2,…,Cc}为集合X所属的c个类的集合. 则模糊类可由下类式子定义:
(1) 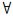 xk∈X,
xk∈X,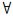 Ci∈P,0≤μCi(xk)≤1;
Ci∈P,0≤μCi(xk)≤1;
(2) 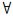 xk∈X,
xk∈X,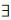 Ci∈P,满足μCi(xk)>0;
Ci∈P,满足μCi(xk)>0;
(3) 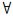 xk∈X,
xk∈X,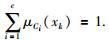
式中,μCi(xk)为隶属度函数,表示xk隶属于类Ci的程度.
定义目标函数JRFCM如下:

其中,p为隶属度函数指数,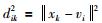 ,vi为第i(i=1,2,…,c-1)个类中心变量. 对于噪声类,即第c个类,有:
,vi为第i(i=1,2,…,c-1)个类中心变量. 对于噪声类,即第c个类,有:

参数δ为噪声类半径,可选取文[22]中的计算公式实现自动更新:
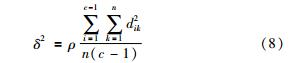
隶属度函数μCi(xk)和聚类中心vi通过以下公式迭代计算:
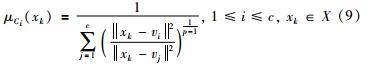
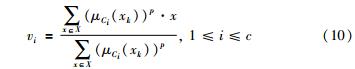
基于模糊聚类的数据融合算法主要思路是: 采用模糊聚类方法将当前同时刻的多源感知数据分为两类,即正常类和异常类. 计算正常类的类中心作为融合结果,异常类数据作为故障数据不参与融合计算. 所采用的模糊聚类方法在上面提到的RFCM聚类方法基础上引入式(5)统计权值λ来修正隶属度函数指数,则目标函数可修改为
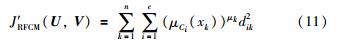
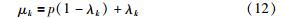
式中μk为调整后的隶属度函数指数. 由于受λk乘子的影响,μ在(1,p)区间内变化,且(μCi(xk))μk随λk增大而增大. 这表明,历史数据具有较小方差值的传感源在当前融合过程中对于融合结果影响更大,从而达到历史融合结果指导当前融合过程的目的.
相应地,式(9)和(10)修改为
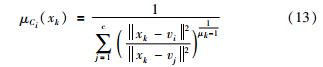
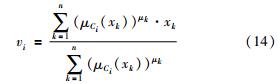
其中,1≤i≤c,1≤k≤n. 融合计算迭代过程如图3所示. 隶属度函数矩阵初始化为U0=[λ; (1-λ)].
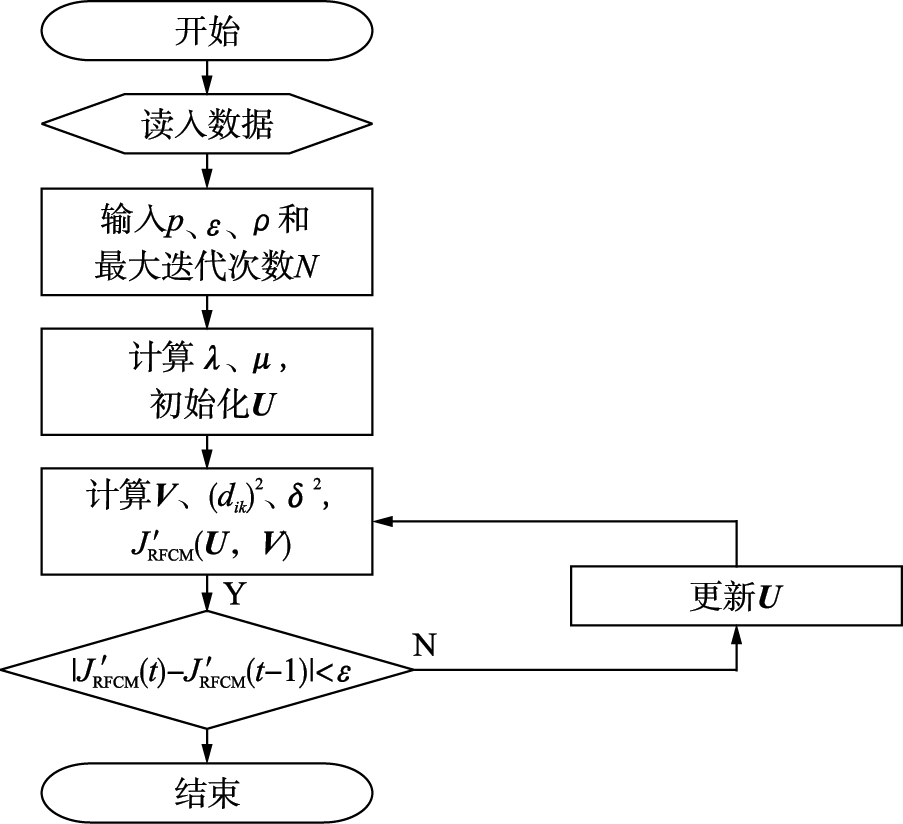 |
| 图 3融合算法计算流程图 Fig. 3 Fusion algorithm flow chart |
为验证所提方法的融合效果,本文分别用4组数据对方法进行实验,并与自适应加权平均、传统FCM聚类融合方法相对比,进而验证算法的有效性和优越性.
实验1 采用文[19]中多传感器数学模型生成的样本数据进行仿真测试. 该模型由5个传感源组成,具体表达式如下: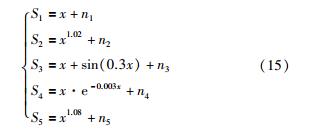
式中,Si为第i个传感器的真实测量值,x为目标对象实际值,ni为随机白噪声,噪声方差σ2=1.5. 另外在S3和S4中分别加入两个异常值作为粗大误差. 可以看出,S4、S5所对应的传感器具有一定的系统误差.
原数据图像与应用3种方法的融合结果图像如图4所示.
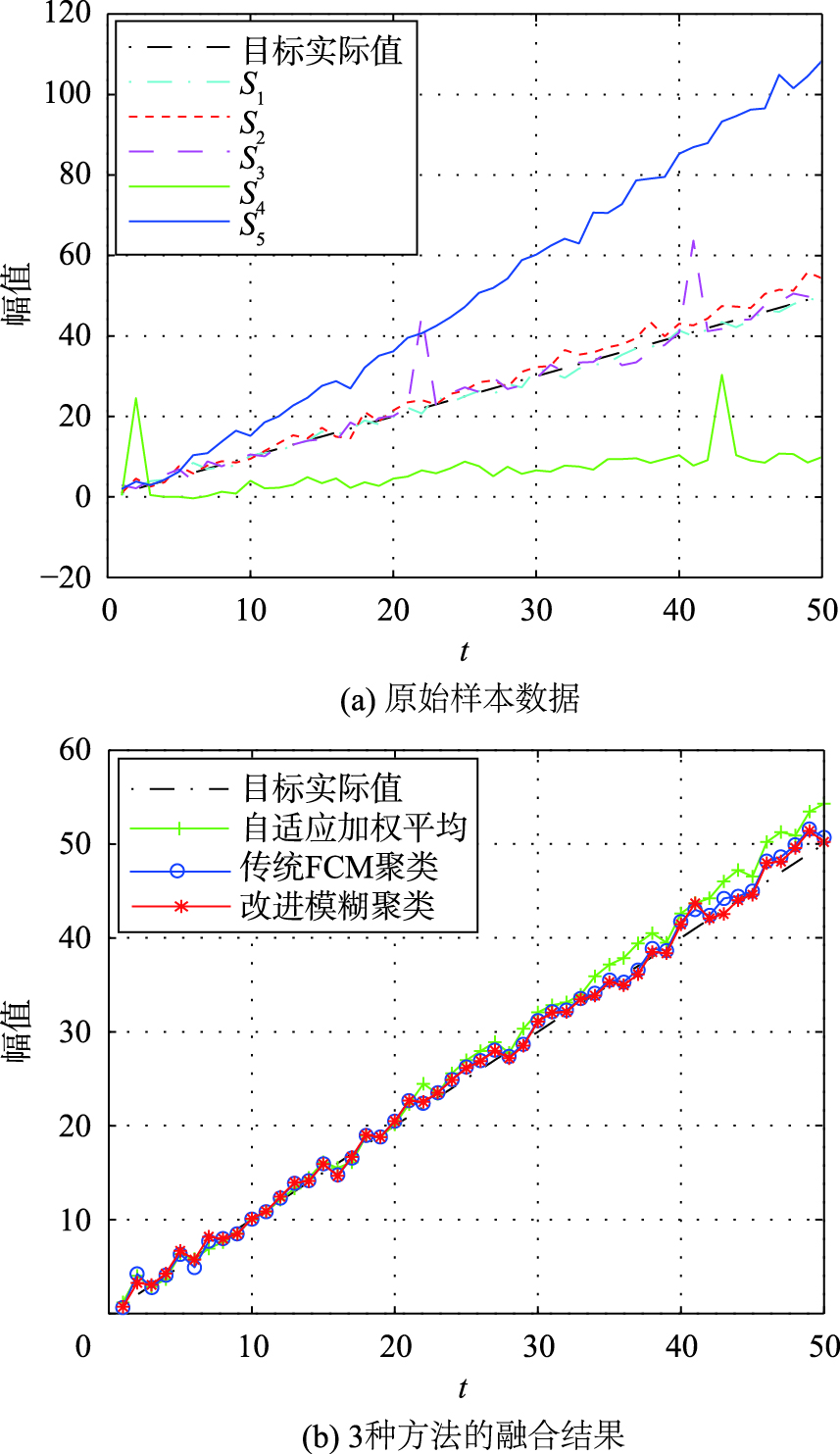 |
| 图 4 第1组测试数据及融合结果对比图 Fig. 4 The first group samples and comparison of the fusion results |
从图4(a)可见,随着时间的增加,S4、S5相比于S1、S2、S3具有更大的系统误差,即同一时刻t下,Z4与Z5分别在不同方向远离真实值. 图4(b)中,在t=25之前,3种方法的融合效果都比较理想; 而在t=25以后,随着Z4、Z5与真实值距离的加大,自适应加权平均方法的融合误差较其它两种方法要大,表明该方法受到传感源“异常”的影响较大. 另外,图4(b)也表明3种融合方法对粗大误差均不敏感.
实验2 采用系统误差具有明显分类特征的多传感器数学模型进行测试. 模型具体表达式如下:
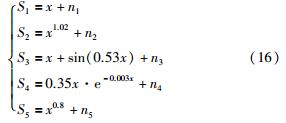
噪声方差σ2=1.5,另外在S3和S4中分别加入两个异常值作为粗大误差. 原数据图像与应用3种方法的融合结果图像如图5所示.
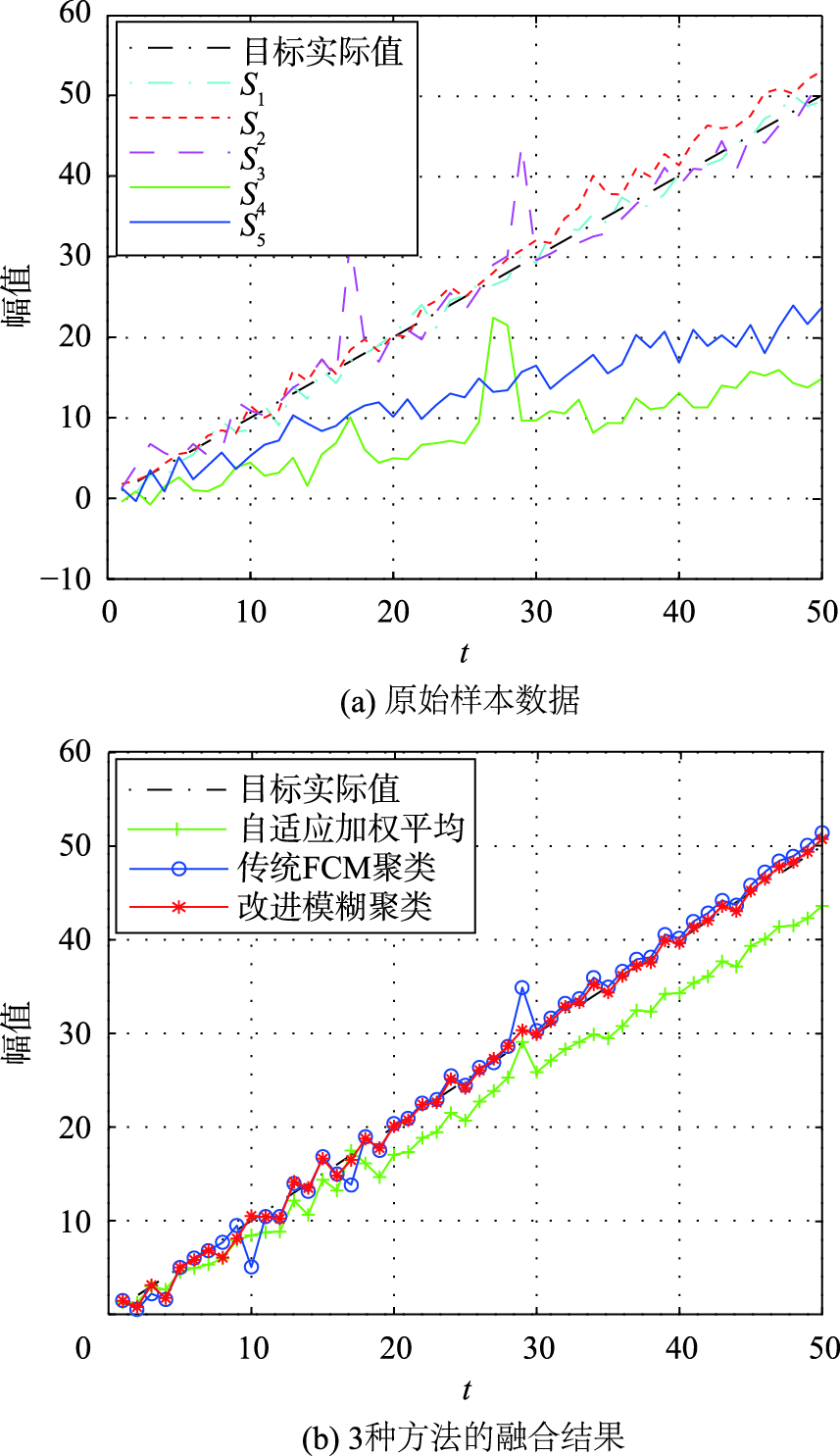 |
| 图 5 第2组测试数据及融合结果对比图 Fig. 5 The second group samples and comparison of the fusion results |
图5(a)中,S4与S5的观测值Z4与Z5出现了同一方向远离,且相互距离较近. 受此影响,图5(b)的融合结果中,自适应加权平均融合方法在t=10之后出现了较大的融合误差,且误差随着时间t而不断增大. 这表明,当多传感器系统存在单侧系统误差时,自适应加权平均方法会受到传感源更大“异常”的影响而导致融合结果失真. 另外,图5(b)也表明该系统下3种融合方法对粗大误差均不敏感.
实验3 采用具有零系统误差、不同随机误差的多传感器数学模型进行测试,模型具体表达式如下:
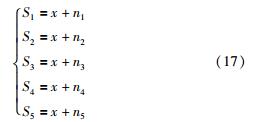
式中ni(i=1,2,…,5)对应的方差分别为σ12=1.5,σ22=3.0,σ32=3.25,σ42=4.5,σ52=5.25. 同样在S3和S4中分别加入2个异常值作为粗大误差. 原数据图像与应用3种方法的融合结果图像如图6所示.
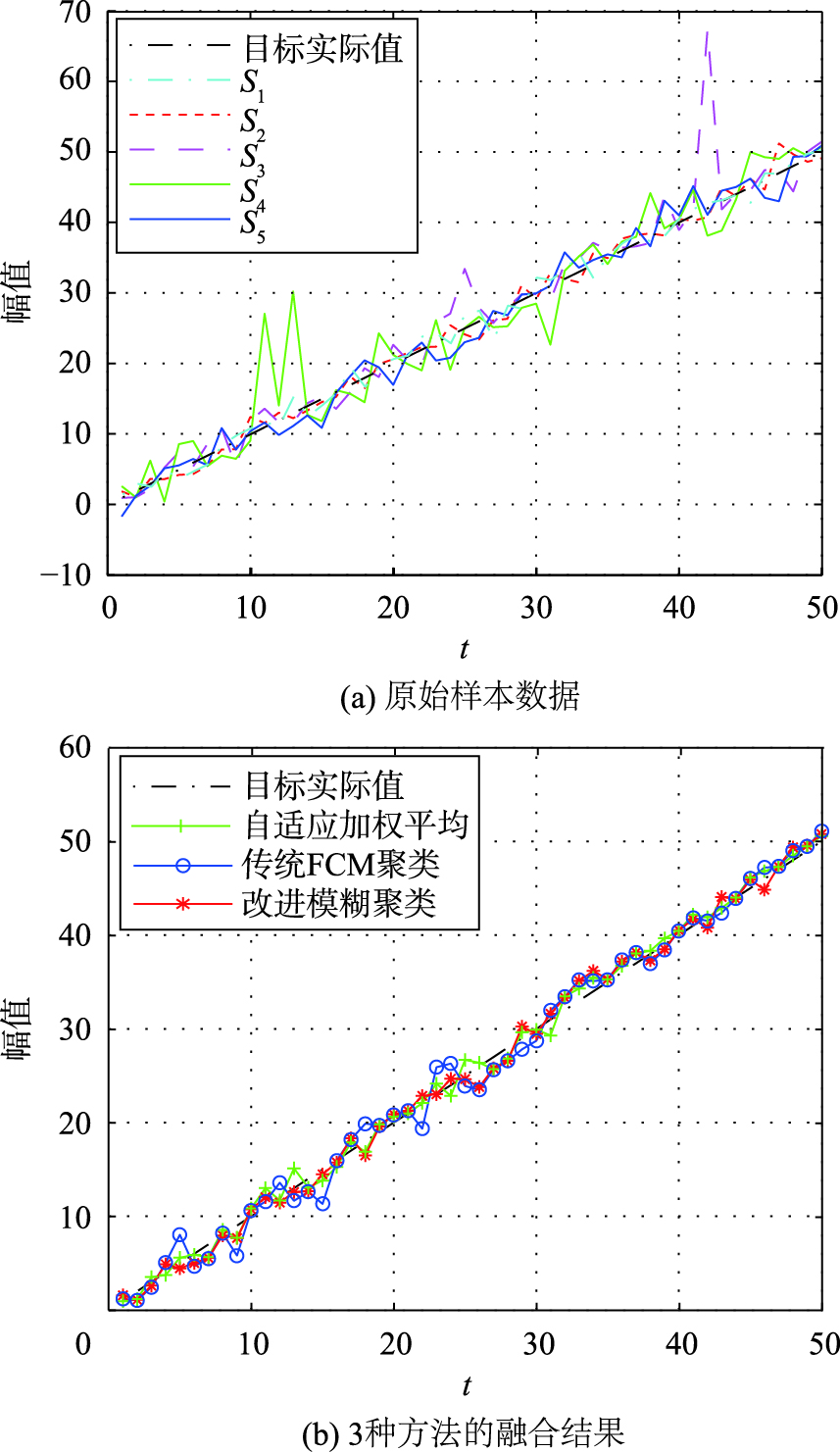 |
| 图 6 第3组测试数据及融合结果对比图 Fig. 6 The third group samples and comparison of the fusion results |
从图6(b)的融合结果中可以看出,在系统误差为0、随机误差大小不同且有一定粗大误差的前提下,3种方法均能够得到与真实值变化趋势相一致的融合结果,累计误差无特别明显的区分. 定量的累计误差分析将在后面性能测试中给出.
实验4 采用具有震荡特征的多传感器数学模型进行测试(σ2=0.01). 模型具体表达式如下:
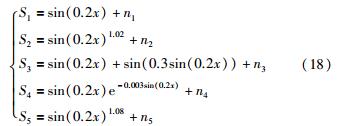
同样在S3和S4中分别加入4个异常值作为粗大误差. 原数据图像与应用3种方法的融合结果图像如图7所示.
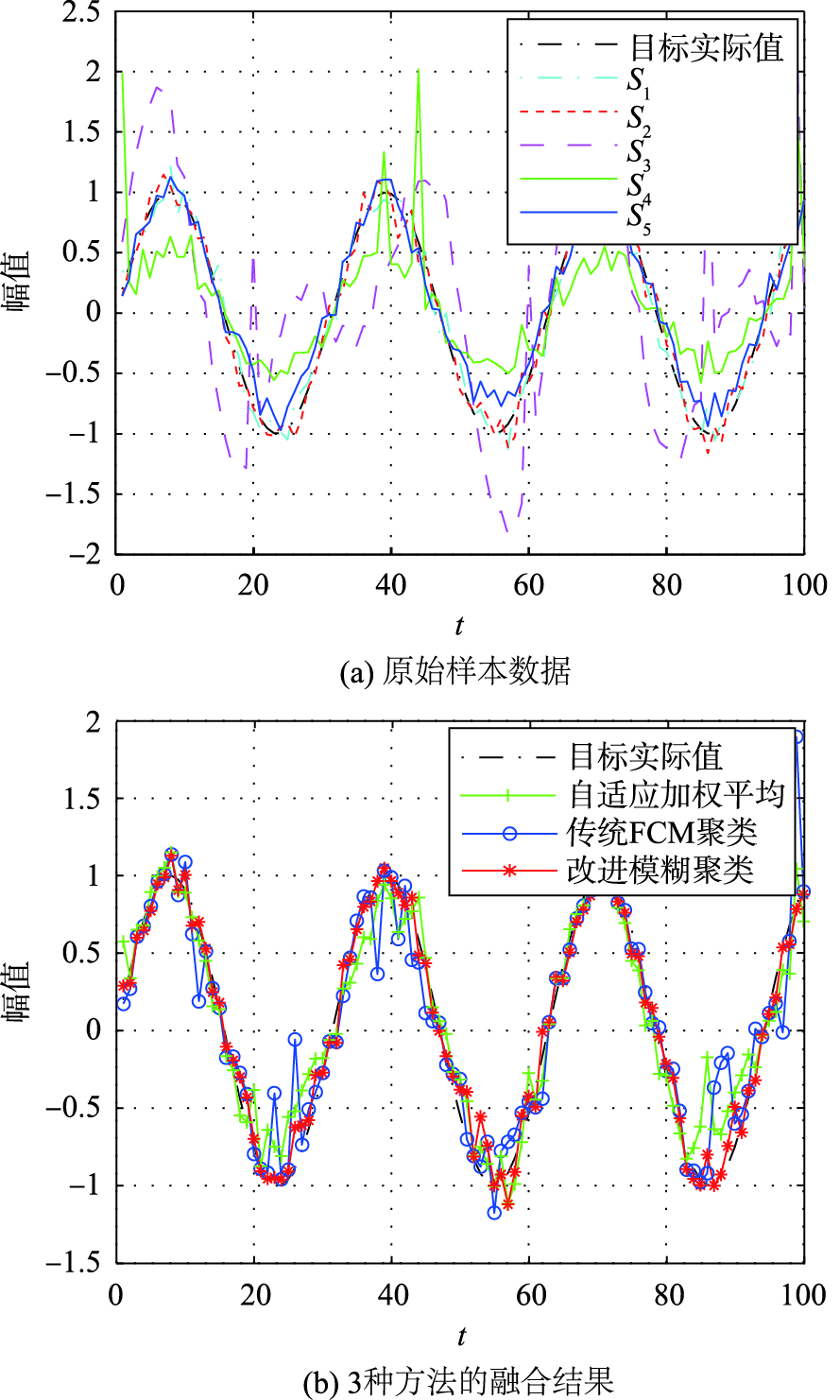 |
| 图 7 第4组测试数据及融合结果对比图 Fig. 7 The forth group samples and comparison of the fusion results |
从图7(b)中可以比较清晰地看到,所提出的改进模糊聚类融合方法能够比较准确地反映出目标真实值,而传统的FCM融合方法融合结果偏离真实值较远,表明具有较大的融合误差.
4.2 性能分析与测试首先从数学原理层面分析3种方法对融合精度的影响. 传统的自适应加权平均融合方法中权值的确定是在总均方差最小的最优条件下确定的. 显然,当多传感器系统仅具有随机误差时,通过自适应加权平均方法所获得的融合结果较真值偏差最小,融合结果最佳[8]. 但当传感器之间存在明显的、具有非随机特征的系统误差时,各传感源测量值不再是真实值的无偏估计,因此融合结果较真值必然存在较大偏差,这一点在实验2中得以印证.
基于模糊C均值聚类的融合方法通过对各个观测数据进行模糊聚类,将包含多个观测值的“大类”的类中心作为融合结果[18]. 由于模糊C均值聚类方法的目标函数是基于总方差最小规则确定的(见式(6)),因此在仅有随机误差条件下,其融合结果也接近于真实值. 该方法的优点在于能够剔除掉带有规律性偏移的测量值对融合结果的影响,缺点在于: 1) 类的个数的确定直接影响融合结果的准确性; 2) 仅分析当前结果,无法考虑和借鉴历史经验结果.
本文所提方法在基于模糊C均值聚类融合方法基础上,通过引入噪声类解决了聚类个数确定的问题; 通过在当前融合中引入隶属度函数影响因子增加了历史经验对当前计算的影响,进而在一定程度上使得融合结果(聚类中心)更加接近真实值.
为了定量地分析算法的融合精度,利用3种方法分别对4个模型生成的不同的10组数据进行融合实验,统计计算10组实验中3种方法的平均融合误差. 实验结果见表1.
| 模型1 | 模型2 | 模型3 | 模型4 | |
| 自适应加权平均 | 2.06 | 3.95 | 0.91 | 0.25 |
| 传统FCM聚类 | 1.18 | 1.08 | 1.62 | 0.31 |
| 改进的模糊聚类 | 1.04 | 1.06 | 1.21 | 0.18 |
从表1中可以看出,对于4种不同类型的系统数据,本文提出的改进模糊聚类融合方法较传统FCM聚类融合方法具有更高的融合精度; 自适应加权平均虽然能够在无系统误差的多传感器融合中获得更高的融合精度,但对于具有明显单向偏移的系统误差条件下,融合结果将会有明显的偏差. 因此,综合来看,本文所提方法较其它两种方法更有优势.
为了比较3种方法在计算用时方面的性能,利用3种方法分别对4个模型生成的同一组数据、在同一硬件平台下进行融合实验,得到各组计算用时数据. 实验结果见表2.
| 模型1 | 模型2 | 模型3 | 模型4 | |
| 自适应加权平均 | 0.000 2 | 0.000 3 | 0.000 2 | 0.026 0 |
| 传统FCM聚类 | 0.176 7 | 0.180 3 | 0.170 5 | 0.487 8 |
| 改进模糊聚类 | 0.033 5 | 0.041 0 | 0.052 1 | 0.195 0 |
从表2中可以看出,自适应加权平均融合方法较其它两种方法在计算用时方面具有较明显的优势; 而本文提出的改进模糊聚类融合方法较传统FCM聚类方法具有更少的计算用时.
5 结论针对同源同构传感器构成的多传感器系统在数据层融合的具体需求,本文提出一种基于改进模糊聚类的同源同构感知序列在线融合方法. 该方法不仅具有传统基于FCM聚类的数据融合方法在无需先验知识、无需系统模型、支持系统扩展(即传感节点增减)、计算简单、可在线应用等方面的优点,通过改变融合策略并引入噪声类,有效避免了传统模糊聚类融合方法中对聚类数设定的问题,同时有效去除了偏移较大的数据源和异常信号对融合结果的不良影响. 算法中引入了隶属度函数影响因子,增加历史融合结果对当前融合的指导,避免了初始参数选择的盲目性和随机性,有助于避免局部极值问题. 实验结果表明,该方法较基于FCM聚类融合方法具有更好的鲁棒性和融合精度,同时比传统自适应加权平均融合方法具有更大的适应性.
| [1] | Kroger T, Wahl F M. Multi-sensor integration and sensor fusion in industrial manipulation: Hybrid switched control, trajectory generation, and software development[C]//Proceedings of IEEE International Conference on Multi-sensor Fusion and Integration for Intelligent Systems. Piscataway, NJ, USA: IEEE, 2008: 411-418. |
| [2] | 金学波, 林岳松, 章辉. 应用于状态监测的多传感器融合估计[J]. 控制理论与应用, 2009, 26(3): 296-298. Jin X B, Lin Y S, Zhang H. Multisensor fusion estimation in state monitoring[J]. Control Theory & Applications, 2009, 26(3): 296-298. |
| [3] | Okatan A, Hajiyev C, Hajiyeva U. Fault detection in sensor information fusion Kalman filter[J]. International Journal of Electronics and Communications, 2009, 63(9): 762-768. |
| [4] | Bath W G, Boswell C M, Sommerer S, et al. Detection systems information fusion[J]. Johns Hopkins APL Technical Digest, 2005, 26(4): 306-313. |
| [5] | 杨小军, 潘泉, 梁彦, 等. 基于粒子滤波和检测信息的多传感器融合跟踪[J]. 信息与控制, 2005, 34(3): 356-359. Yang X J, Pan Q, Liang Y, et al. Multi-sensor fusion tracking based on particle filtering and detection information[J]. Information and Control, 2005, 34(3): 356-359. |
| [6] | Sung W T, Tsai M H. Multi-sensor wireless signal aggregation for environmental monitoring system via multi-bit data fusion[J]. Applied Mathematics & Information Sciences, 2011, 5(3): 589-603. |
| [7] | Sun H G, Wang W S, Cao Y. Application of fuzzy data fusion in multi-sensor environment monitor[C]//Proceedings of International Conference on Computational Intelligence and Security. Piscataway, NJ, USA: IEEE, 2009: 550-553. |
| [8] | 李战明, 陈若珠, 张保梅. 同类多传感器自适应加权估计的数据级融合算法研究[J]. 兰州理工大学学报, 2006, 32(4): 78-82. Li Z M, Chen R Z, Zhang B M. Study of adaptive weighted estimate algorithm of congeneric multi-sensor data fusion[J]. Journal of Lanzhou University of Technology, 2006, 32(4): 78-82. |
| [9] | 段战胜, 韩崇昭, 陶唐飞. 基于最近统计距离的多传感器一致性数据融合[J]. 仪器仪表学报, 2005, 26(5): 478-481. Duan Z S, Han C Z, Tao T F. Consistent multi-sensor data fusion based on nearest statistical distance[J]. Chinese Journal of Scientific Instrument, 2005, 26(5): 478-481. |
| [10] | 翟翌立, 戴逸松. 多传感器数据自适应加权融合估计算法的研究[J]. 计量学报, 1998, 19(1): 69-75. Zhai Y L, Dai Y S. Study of adaptive weighted fusion estimated algorithm of multisensor data[J]. Acta Metrologica Sinica, 1998, 19(1): 69-75. |
| [11] | 王炯琦, 周海银, 吴翊. 基于最优估计的数据融合理论[J]. 应用数学, 2007, 20(2): 392-399. Wang J Q, Zhou H Y, Wu Y. The theory of data fusion based on state optimal estimation[J]. Mathematica Applicata, 2007, 20(2): 392-399. |
| [12] | Smaili C, El Najjar M E, Charpillet F. Multi-sensor fusion method using dynamic Bayesian network for precise vehicle localization and road matching[C]//Proceedings of the 19th IEEE International Conference on Tools with Artificial Intelligence. Piscataway, NJ, USA: IEEE, 2007: 146-151. |
| [13] | Zheng Y J, Niu R X, Varshney P K. Sequential Bayesian estimation with censored data for multi-sensor systems[J]. IEEE Transactions on Signal Processing, 2014, 62(10): 2626-2641. |
| [14] | Fan S L, Li D G, Zhao J M. An mine multi-sensor maximum likelihood estimation data fusion algorithm[J]. Journal of Information & Computational Science, 2013, 10(12): 3809-3814. |
| [15] | 雷晓锋, 朱波. 基于多传感器数据融合的微下击暴流感知[J]. 信息与控制, 2011, 40(3): 296-301. Lei X F, Zhu B. Perception of microburst based on multi-sensor data fusion[J]. Information and Control, 2011, 40(3): 296-301. |
| [16] | Fincher D W, Mix D F. Multi-sensor data fusion using neural networks[C] //Proceedings of IEEE International Conference on Systems, Man and Cybernetics.Piscataway, NJ, USA: IEEE, 1990: 835-838. |
| [17] | Tang A H, Zhang Y M. Application of fuzzy clustering in multi-sensor information fusion[J]. Journal of Theoretical and Applied Information Technology, 2012, 45(2): 661-667. |
| [18] | Runkler T A, Sturm M, Hellendoorn H. Model based sensor fusion with fuzzy clustering[C]//Proceedings of IEEE International Conference on Fuzzy Systems at the World Congress on Computational Intelligence. Piscataway, NJ, USA: IEEE, 1998: 1377-1382. |
| [19] | Jaradat M A K, Langari R. A hybrid intelligent system for fault detection and sensor fusion[J]. Applied Soft Computing, 2009, 9(1): 415-422. |
| [20] | 史丽萍, 孙宝元. 传感器动态误差的修正方法[J]. 黑龙江大学自然科学学报, 2003, 20(1): 67-70. Shi L P, Sun B Y. The ways of amending dynamic error by using sensors[J]. Journal of Natural Science of Heilongjiang University, 2003, 20(1): 67-70. |
| [21] | Cimino M G C A, Frosini G, Lazzerini B, et al. On the noise distance in robust fuzzy C-means[J]. International Journal of Computer Science and Engineering, 2007, 1(1): 634-637. |
| [22] | Dave R N. Characterization and detection of noise in clustering[J]. Pattern Recognition Letters, 1991, 12(2): 657-664. |



