2. 江西省民政学校, 江西南昌 330013;
3. 上海理工大学光电信息与计算机工程学院, 上海 200093
2. Jiangxi Province Civil School, Nanchang 330013, China;
3. School of Optical-Electrical and Computer Engineering, University of Shanghai for Science & Technology, Shanghai 200093, China
1 引言
基于视觉的行人检测技术对车辆的安全驾驶及行人的生命安全具有十分重要的作用,已成为智能车辆、 计算机视觉和模式识别等领域的前沿研究课题[1]. 由于交通场景复杂、 障碍物种类多、 行人姿态易变等原因,行人辨识问题一直未能取得满意的解决办法[2 ,3]. 特征提取是行人检测的关键技术,特征选择的好坏直接影响PD(pedestrian detection)分类器的分类精度和运行速度. 边界由目标在图像平面上的轮廓所描述,是目标的重要外形特征,在目标检测和识别中有着十分重要的作用[4 ,5]. 由于交通场景的复杂性,行人轮廓曲线的提取一直未能取得好的效果.
活动轮廓模型,也称Snake模型[6],它将目标的初始几何特性及其所在图像的先验知识相结合,运用动力学知识推理曲线的变形过程,最终得到目标的边界曲线. 经过不断改进和发展,形成了经典Snake模型[6]、 气球模型、 距离模型[7]、 GVF模型[8 ,9]等多种参数式Snake模型,它们在单目标边界提取中有着独特的优势[10]. 目前,Snake模型主要用于图像分割[11 ,12]、 轮廓提取[13 , 14]等,由于自身固有的缺陷,如对图像噪声敏感、 对初始轮廓形状及其位置要求严格、 难以收敛到凹型边界、 收敛速度较慢等,目前主要用于医学图像等少数领域[15 ,16]. 为了克服Snake模型对图像噪声敏感、 初始轮廓设置困难、 收敛速度慢等缺陷,本文将角点检测技术和GVF模型相结合,提出抗噪的Snake模型,同时针对GVF模型的缺陷提出初始轮廓曲线优化方法及相适应GVF场的建立方法.
为了成功提取交通视图中行人的轮廓曲线,本文将Snake模型和立体分割技术相结合,先将潜在行人目标从交通视图分割出来[17 , 18],然后用抗噪Snake模型提取行人轮廓曲线. 本文以多个交通场景下的行人为分析对象,验证抗噪Snake模型在行人轮廓提取中的效果.
2 基于视觉的立体分割双目立体视觉是人类视觉系统的有效模拟,通过它可以获取环境的三维信息,目前已成功运用于三维重建、 目标分割、 导航及虚拟现实等领域.
立体匹配是立体视觉的关键技术,不同的算法有着不同匹配速度及精度. 基于区域的立体匹配算法可获得稠密视差,可有效运用于目标的定位和分割. 但是,该算法对弱纹理区域比较敏感且速度相对较慢. 而基于特征的立体匹配算法可获得较为准确的稀疏视差,运行速度快,但要得到稠密视差,需经过数值插值.
文[17]提出基于边界检索的特征匹配算法,该算法可提取出基于边缘视差的目标分割图,具体分割过程为:
(1) 基于Canny算子的边缘提取;
(2) 基于边缘检索的立体匹配;
(3) 视差图的XZ平面投影;
(4) 依据高度信息去除路面点;
(5) 根据深度信息在XZ平面完成目标分割;
(6) XY平面反向投影,得到基于边缘的目标分割图.
3 Snake模型 3.1 经典Snake模型经典Snake模型由Kass在1987年提出,用一条参数曲线C(s)=(x(s),y(s)),s∈[0,1]表示,通过最小化式(1)所示的能量泛函,该曲线能够在待处理图像I上移动并最终收敛到待分割目标的边界上[6]:
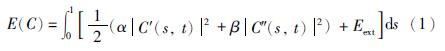
曲线C(s)的形变过程是E(C)的最小化过程,通过变分法求解式(1)的能量最小化问题,得到式(2)所示的平衡方程:
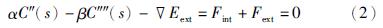
 为梯度运算符,
为梯度运算符, Eext为外力Fext式(2)对应时域动态演化方程为
Eext为外力Fext式(2)对应时域动态演化方程为
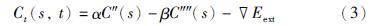
经典Snake模型存在如下主要缺陷: 初始轮廓必须接近真实边界、 难以收敛到凹陷边界、 易受噪声干扰等.
3.2 GVF模型Xu等[8 ,9]提出一种由光流场原理得来的稠密向量场,称为梯度向量流GVF,并将此力代替传统Snake模型中Fext,构成了GVF模型,即将式(3)替换为
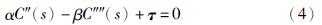
在此,GVF表示为矢量场τ(x,y)=[u(x,y),v(x,y)],对应边界图f(x,y)的最小化能量泛函ε为
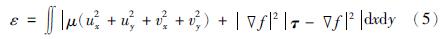
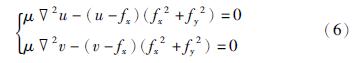
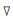 2为拉普拉斯算子,fx、 fy分别为f对x、y的偏导数.
2为拉普拉斯算子,fx、 fy分别为f对x、y的偏导数.
将u、 v分别看成时间的函数,通过式(7)、 (8)所示的迭代运算方程可实现式(6)中u、v的求解,从而得到基于待处理目标区域I的GVF矢量场.
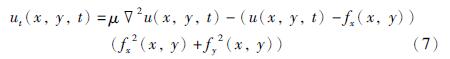
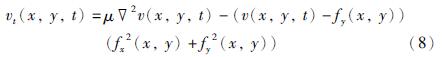
GVF模型通过对外部能量的改进,扩大了外力的作用范围,有效地克服了不能收敛到凹陷轮廓边界的缺陷,对初始轮廓设置的敏感性也有了较大程度的改善,是目前较为成熟和通用的Snake模型. 但是,GVF场由边界梯度向量迭代而来,对迭代次数较为敏感,很难确定最佳迭代次数且计算复杂;同时,初始轮廓设置仍较为敏感和困难,直接影响轮廓收敛速度;此外,GVF模型需以提取目标真实边界f(x,y)为前提,轮廓提取过程易受边界噪声干扰.
4 基于GVF模型的抗噪Snake模型虽然GVF模型能有效解决Snake模型的诸多不足,但仍存在自身缺陷. 目前,它主要运用于医学影像等背景固定和目标简单的应用领域. 本文以道路交通中的行人为研究对象,由于交通视图分辨率较低、 背景复杂多变、 行人姿态易变等特性,基于边界的行人分割图中仍包含一定数量的边界噪声,使运用Snake模型提取的行人轮廓曲线存在一系列“毛刺”现象,即噪声所引起的噪声角点,如图 1(a)所示. 为了提高Snake模型在行人轮廓提取中的抗噪能力,将GVF模型及角点检测技术相结合,提出基于GVF模型的抗噪Snake模型. 此外,该模型还运用了初始轮廓优化、 自适应GVF场的建立等技术.
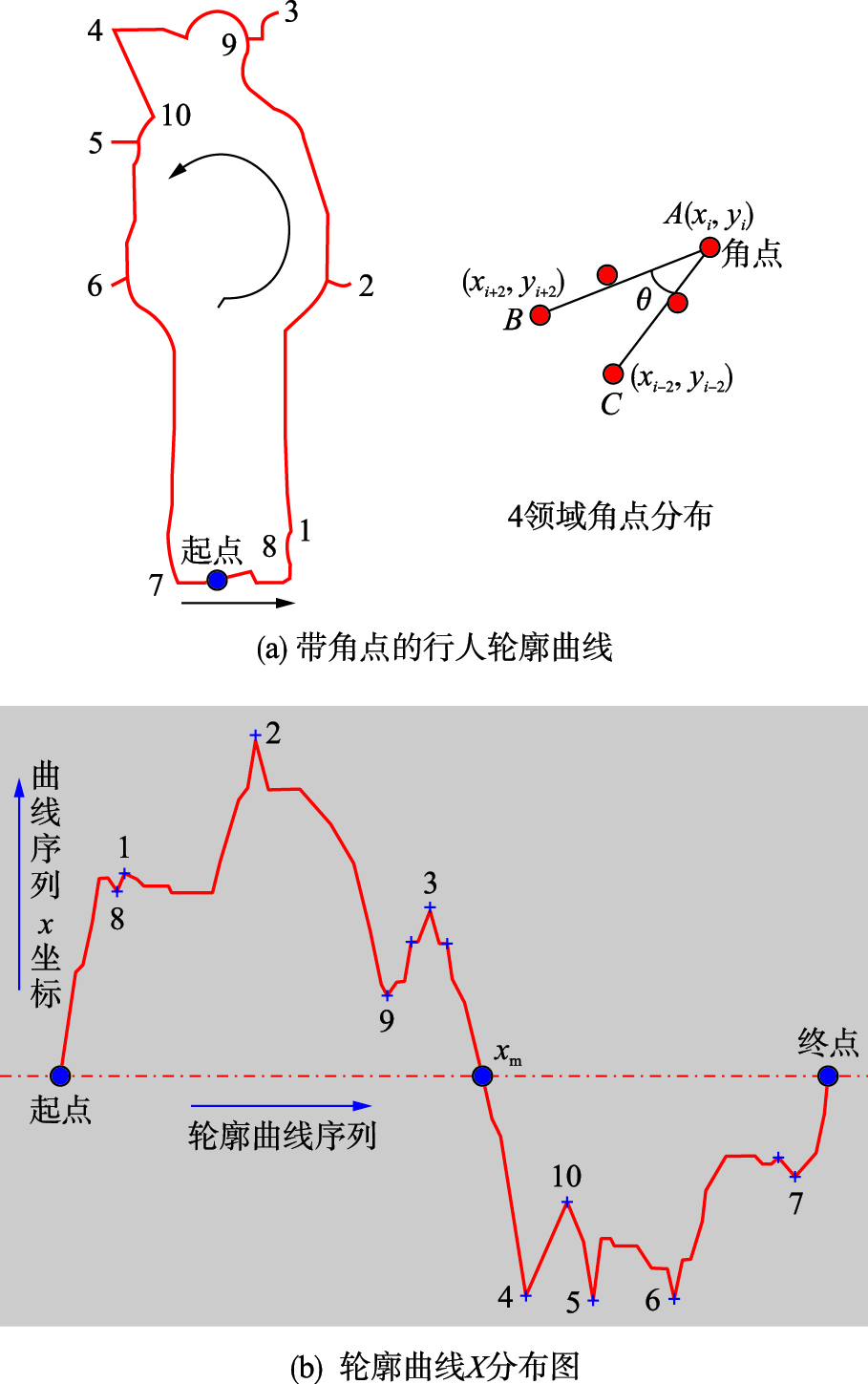 |
| 图 1 轮廓曲线的角点分析Fig. 1 Corner analysis for contour curve |
4.1 基于轮廓曲线的角点检测
角点是目标轮廓线上曲率超过一定阈值的局部极值点[19 ,20]. 基于轮廓曲线的角点检测有角点强度K法、 曲率极值法、 多尺度角点检测法等不同算法. 其中,角点强度K值法易受噪声干扰; 曲率极值法需建立曲线方程,运算量较大; 而多尺度角点检测法需合理确定滤波器的尺度,运算复杂[14]. 因此,本文针对图 1(a)所示的行人轮廓曲线角点问题,提出了基于轮廓曲线的角点检测方法.
如图 1(a)所示,角点1~7沿图示逆时针观测均为外凸点,由噪声引起,称为噪声角点; 角点8~10沿逆时针观测为内凹点,位于目标边界之上,称为边界角点. 若将轮廓曲线序列从起点开始按x坐标(也即横坐标)将其顺时针展开,可得到图 1(b)所示的X分布图,图示横坐标为轮廓曲线序列标号,纵坐标对应各点序列的x坐标. 图中带“*”号的点为极值点,和图 1(a)所示角点相对应. 同理,亦可建立轮廓曲线Y分布图,得到y值极点分布图.
若以轮廓曲线X中值xm为水平分界线,可将轮廓曲线X分布图分成图示上下两部分. 由图可知,噪声角点分别对应X分布图上半侧的极大值及下半侧的极小值; 噪声角点外凸程度和角点长度(即角点两侧轮廓点数量)成正比,且所对应曲率普遍较大(即角点及其轮廓点所形成的夹角θ较小). 同理,Y分布图中的噪声角点和X分布情况一致. 为此,可通过检测噪声角点长度及其曲率来筛选外凸严重的噪声角点.
针对受噪声干扰而形成的带角点轮廓曲线,本文提出如下噪声角点检测算法:
(1) 分别以xm、 ym为水平轴将轮廓曲线X分布图及Y分布图分成上下两部分;
(2)分别计算X分布图及Y分布图上侧的极大值Xmax、 Ymax及下侧的极小值Xmin、 Ymin;
(3)按图 1(a)所示4领域角点法计算[Xmax、 Xmin]、 [Ymax、 Ymin]中各角点夹角θ,并将对应θ较小(如θ<30°)的角点判别为噪声角点,记为Xnoise、 Ynoise;
(4)将Xnoise、 Ynoise合并为XYnoise,即确定噪声角点位置.
4.2 初始轮廓设置及自适应GVF场的建立初始轮廓曲线设置及GVF场的建立是轮廓提取的重要内容,它们不仅影响轮廓曲线的正确收敛,同时还制约着轮廓收敛速度. 尽管GVF模型通过扩大Fext的作用范围改善了初始轮廓的设置问题,但这是以建立覆盖整个图域的GVF场为代价的. 而且GVF场的迭代过程非常复杂,时耗与迭代次数成正比. 此外,轮廓曲线的收敛过程也较为复杂,相应时间开销与初始轮廓曲线至边界的距离成正比. 因此,合理设置初始轮廓曲线并建立与之相适应的GVF场十分重要.
本文提出的初始轮廓曲线设置及相适应GVF场的建立过程如下:
(1)连接目标边缘分割图f(x,y)中的最外围边缘点,形成目标初始轮廓曲线C0(s);
(2) 按基于轮廓曲线的角点检测法寻找并去除C0(s)中的角点XYnoise,实现对初始轮廓曲线的优化,使其尽可能逼近真实边界;
(3)以C0(s)中的角点位置坐标XYnoise为依据,去除f(x,y)中相应位置处一定窗口范围内(如3×3)的边缘噪声,得到去除噪声后的边缘分割图f′(x,y),然后按式
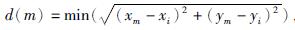
(4)计算边缘距离d的最大值dmax,并以此值为边缘图f′(x,y)对应GVF场的迭代次数Iter_GVF,从而得到和初始轮廓曲线C0(s)相适应的GVF场.
4.3 抗噪Snake模型建立GVF模型以提取目标边界f(x, y)为前提,并计算各边界点的方向梯度,然后按式(6)建立GVF场. 显然,边界噪声对其周边GVF场的建立有较强的控制作用,使GVF场发生畸变,严重影响轮廓曲线的正确收敛,在目标轮廓曲线中形成“毛刺”状的角点. 因此,检测并删除边界噪声十分重要.
基于以上分析,本文提出了如图 2所示的基于抗噪Snake模型的目标轮廓提取操作流程.
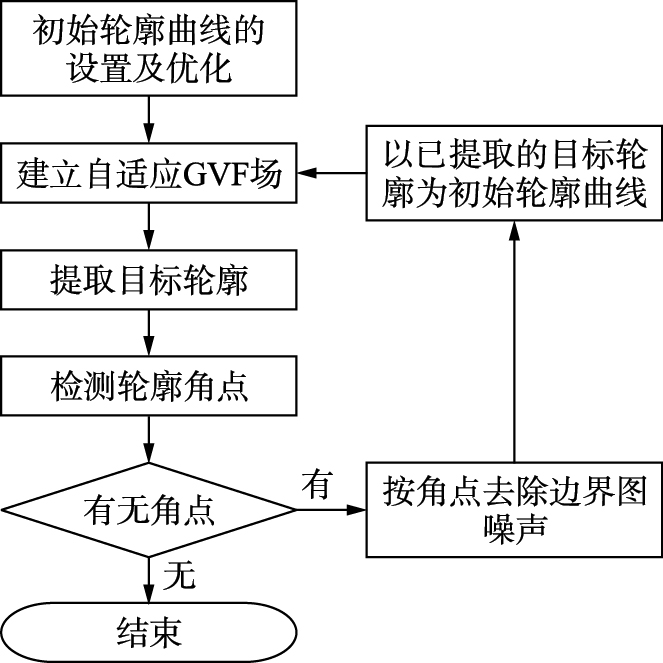 |
| 图 2 基于抗噪Snake模型的目标轮廓提取流程图Fig. 2 Flow chart for object contour extraction based on anti-noise Snake model |
5 实验与分析
本实验以车载立体相机为采集系统,获取了200个包含行人的典型交通场景. 图 3所示为部分行人立体左图,它们具有不同的特征:
 |
| 图 3 行人立体图(左图)Fig. 3 Stereo image of the pedestrian (left image) |
(1) 场景1、 2为静止状态,场景3、 4为运动状态;
(2) 场景1~4中行人分别代表后视、 侧视、 斜视和正视等情形;
(3) 各场景行人携带饰品各异(如背包、 挎包、 书本等).
按文[11]对各行人目标进行立体分割,得到基于边缘视差的行人分割图,如图 4所示. 由于受立体分割算法精度、 交通背景、 图像分辨率等因素的影响,尽管提取出了较为清晰的行人边界图,但仍包含一定数量的离散边界噪声,特别当背景目标距行人较近(如场景1、 4),或路面存在明显阴影或标线(如场景3)时,噪声尤为明显. 因此,为获取连续、 光滑、 闭合、 准确的行人轮廓曲线,需对行人边缘图进行必要的后期处理.
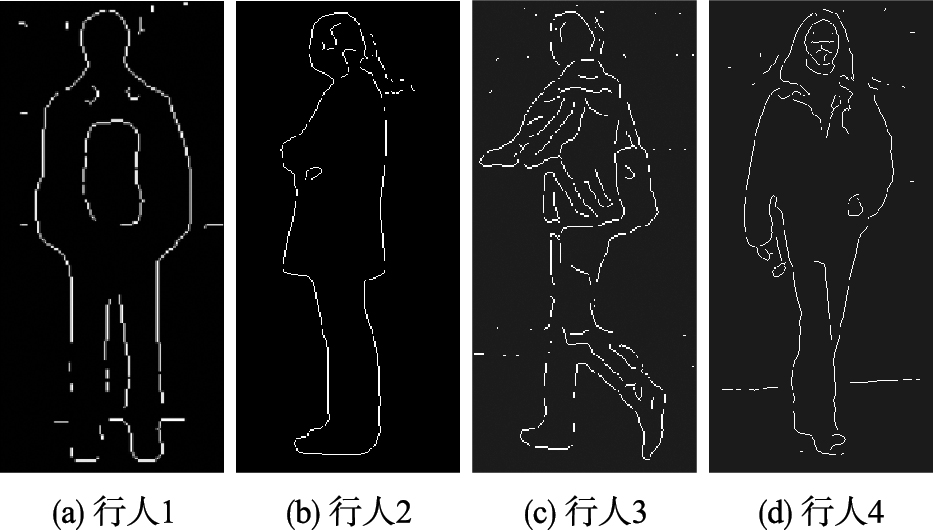 |
| 图 4 基于视差的行人分割图Fig. 4 Pedestrian segmentation maps based on the disparity |
为了测试抗噪Snake模型在行人轮廓曲线提取中的应用效果,分别运用GVF模型以及抗噪Snake模型对图 3所示行人分割目标进行处理.
5.1 基于GVF模型的行人轮廓提取图 5所示为基于GVF模型的行人轮廓提取结果,图 5左侧为轮廓曲线迭代变形轨迹(初始轮廓采用通用的椭圆曲线,如绿线所示),右侧为提取的目标轮廓曲线. 如图所示,在内外力的共同作用下,轮廓曲线C(s,t)不断向目标边界靠拢,得到新的轮廓曲线C(s, t+1) ,由于其周长发生变化(增大或减小)而轮廓点不变,故相邻轮廓点间距发生变化(增大或缩短). 为提高速度和精度,需对C(s, t+1) 中的轮廓点进行插值或删除处理,以使相邻轮廓点间距d位于合适范围内(本文设置d∈(0.5,2),单位pixel),从而得到C′(s, t+1). 如此循环,经过多次迭代处理后,轮廓曲线停留在目标边界上,得到最终目标轮廓曲线. 其中,Iter_GVF_p1=80(行人1中GVF场的迭代次数),Iter_GVF_p2=200,Iter_GVF_p3=300,Iter_GVF_p4=280; Iter_Contour_p1=400(行人1中轮廓曲线迭代变形次数); Iter_Contour_p2=300; Iter_Contour_p3=1 200; Iter_Contour_p4=1 300; 参数α、 β、 μ分别设置为0.1、 0.5、 0.3.
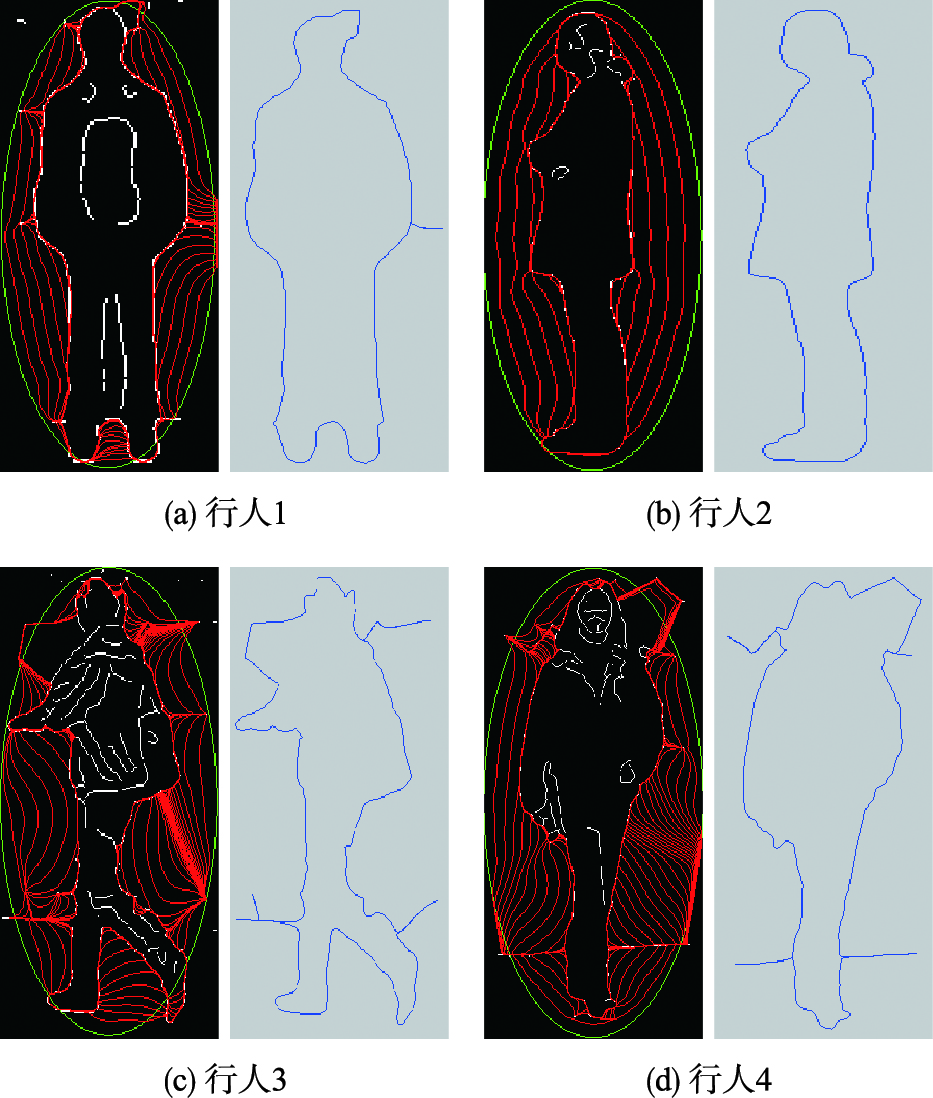 |
| 图 5 基于GVF模型的行人轮廓提取Fig. 5 Pedestrian contour extraction based on GVF model |
由图 5可知,由于噪声的影响,行人1、 3、 4的轮廓曲线均包含一定数量的“毛刺”,发生了不同程度的畸变,行人2由于包含噪声较少而所得轮廓较为理想. 但是由于初始轮廓曲线离目标边界较远,对应的Iter_GVF及Iter_Contour均较大,时耗较长.
5.2 基于抗噪Snake模型的行人轮廓提取以行人3为例,抗噪Snake模型对其处理结果如图 6所示. 其中,图 6(a)为经4.2节步骤(1)所得初始轮廓曲线C0(s),经步骤(2)去角点处理后,得到图 6(b)所示优化后的C0(s); 按步骤(3)、 (4)计算出最大距离dmax=60 pixel,据此绘出图 6(c)所示Iter_GVF=60的GVF场、 图 6(d)所示为Iter_Contour=100的轮廓变形轨迹、 图 6(e)所示为初始行人轮廓. 显然,初始轮廓仍包含一定数量的角点,经过2次循环去噪处理后,得到图 6(g)所示结果,其中图 6(f)为第2次去噪轮廓变形轨迹,对应Iter_GVF=40,Iter_Contour=60. 为便于比较,α、 β、 μ仍取0.1、 0.5、 0.3(下同).
 |
| 图 6 基于抗噪Snake模型的轮廓提取(行人3)Fig. 6 Contour extraction based on anti-noise Snake model(pedestrian 3) |
同理,对行人1、 4进行相应的操作(由于GVF模型可直接提取行人2的完整轮廓,故未加讨论),结果分别如图 7、 图 8所示. 其中,图 7(a)、 8(a)所示为优化后的C0(s),对应Iter_GVF_p1=25,Iter_GVF_p4=50; 图 7(b)、 图 8(b)为提取的初始行人轮廓,相应Iter_Contour_p1=50,Iter_Contour_p4=200; 图 7(c)为经过1次去噪处理后的结果,图 8(c)为经过2次去噪处理后的行人轮廓曲线.
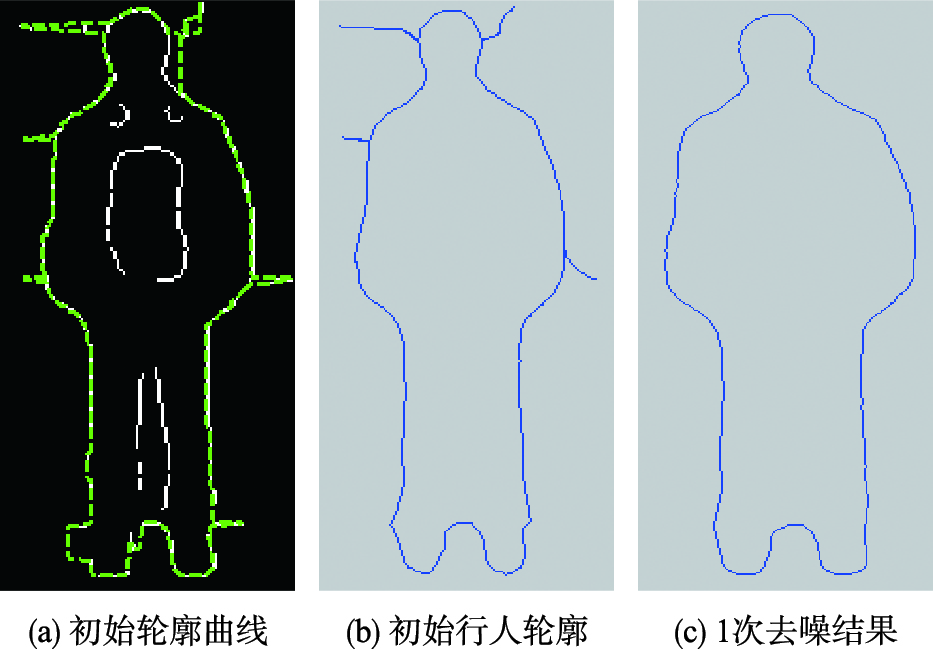 |
| 图 7 基于抗噪Snake模型的轮廓提取(行人1)Fig. 7 Contour extraction based on anti-noise Snake model(pedestrian 1) |
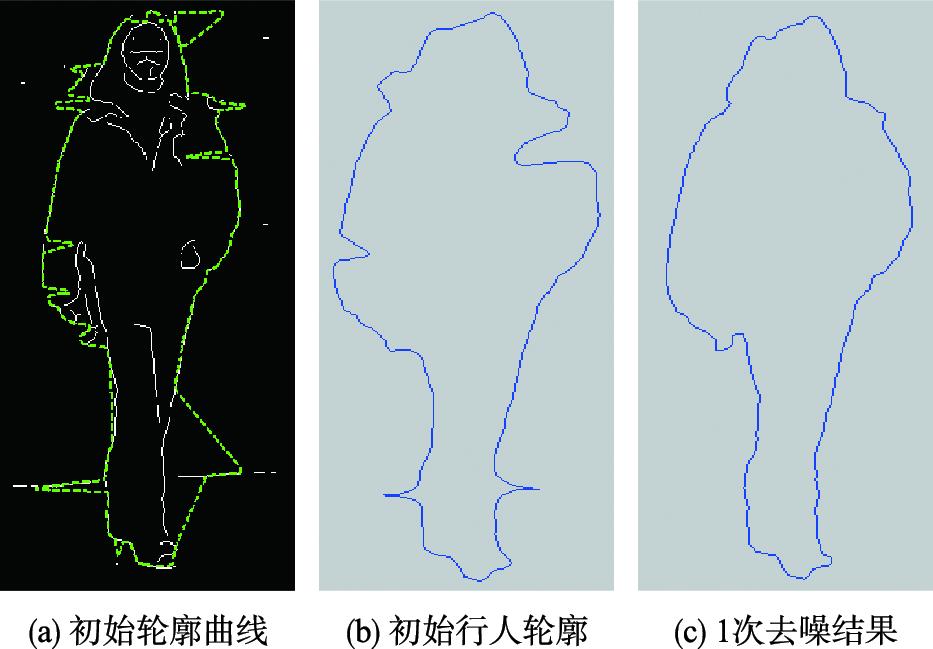 |
| 图 8 基于抗噪Snake模型的轮廓提取(行人4)Fig. 8 Contour extraction based on anti-noise Snake model(pedestrian 4) |
分析上述结果可知,优化后的初始轮廓曲线C0(s)距边界较近且所得行人轮廓曲线比较理想,基本克服了边界噪声的影响,较GVF模型提取结果有了明显的改善.
此外,为了比较GVF模型及抗噪Snake模型对应时间开销,表 1列出了两个模型的Iter-GVF及Iter-Contour. 其中,“GVF”栏为GVF模型,“抗噪”栏代表抗噪Snake模型; 抗噪模型中的Iter-GVF及Iter-Contour均代表各循环去噪阶段数值之和.
| 行人1 | 行人3 | 行人4 | ||||
| GVF | 抗噪 | GVF | 抗噪 | GVF | 抗噪 | |
| Iter_GVF | 80 | 40 | 300 | 120 | 280 | 110 |
| Iter_Contour | 400 | 80 | 1 200 | 260 | 1 300 | 320 |
由表 1可知,抗噪模型在提取行人1的轮廓曲线过程中,其2次循环去噪中的Iter_GVF值累计为40,Iter_Contour累计为80,较GVF模型对应值(80及400)均有很大程度下降. 同时,行人3、 4同行人1具有同样的规律,即抗噪Snake模型较GVF模型在Iter_GVF及Iter_Contour两方面均有很大程度的下降,即抗噪模型的时间成本大大降低.
此外,本文还对另外196个行人场景进行了测试和分析,图 9所示为抗噪Snake模型对低分辨率行人目标的轮廓提取结果. 由图可知,所得行人轮廓总体较好,但由于图像分辨率较低及行人服饰等原因,使提取的行人轮廓曲线存在部分残缺.
 |
| 图 9 抗噪Snake模型对低分辨率行人的轮廓提取Fig. 9 Contour extraction for low-resolution pedestrians using anti-noise Snake model |
综合分析可知,通过对不同场景、 不同图像质量、 不同姿态、 不同状态的行人进行测试和分析,抗噪Snake模型无论在处理速度还是行人轮廓质量方面较GVF模型均有很大程度的改善和提高. 因此,抗噪Snake模型是一种有效的行人轮廓提取方法,同时也验证了基于轮廓曲线的角点检测方法是一种可行的角点检测方案.
6 结论本文将Snake模型的目标轮廓提取能力和立体分割技术相结合,将其成功应用于智能车辆中的行人轮廓提取,有效拓宽了Snake模型的应用领域. 为了提高Snake模型在轮廓提取中的抗噪能力,本文将基于轮廓曲线角点检测技术及GVF模型相结合,提出了基于GVF模型的抗噪Snake模型. 此外,为了克服GVF模型的初始轮廓设置困难及运算过程复杂等问题,本文还提出了一种有效的初始轮廓设置方法,并建立了相适应的GVF场迭代方法. 本文仅对成功分割的行人边缘图进行了相关测试,得到了较为理想的效果. 为了更加深入和全面地分析和研究抗噪Snake模型在行人轮廓提取中的应用,需进一步拓宽研究深度和范围.
| [1] | 苏松志, 李绍滋, 陈淑媛, 等. 行人检测技术综述[J]. 电子学报, 2012, 40(4): 814-820.Su S Z, Li S Z, Chen S Y, et al. A survey on pedestrian detection[J]. Acta Electronica Sinica, 2012, 40(4): 814-820. |
| [2] | Geronimo D, Lopez A M, Sappa A D, et al. Survey of pedestrian detection for advanced driver assistance systems[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(7): 1239-1258. |
| [3] | Borhade S, Shah M, Jadhav P, et al. Advanced driver assistance system[C]//Proceedings of International Conference on Sensing Technology (ICST). Piscataway, NJ, USA: IEEE, 2012: 718-722. |
| [4] | Nguyen D T, Ogunbona P, Li W Q. Human detection with contour-based local motion binary patterns[C]//Proceedings of International Conference on Image Processing. Piscataway, NJ, USA: IEEE, 2011: 3609-3612. |
| [5] | 丁辰瑜, 葛万成, 陈康力. 基于形状上下文的公共场所行人检测系统[J]. 通信技术, 2012, 45(4): 46-49. Ding C Y, Ge W C, Chen K L. Pedestrian detection for public place based on shape context[J]. Communications Technology, 2012, 45(4): 46-49. |
| [6] | Kass M, Witkin A, Terzopoulos D. Snakes: Active contour models[J]. International Journal of Computer Vision, 1988, 1(4): 321-331. |
| [7] | Cohen L D, Cohen I. Finite-element methods for active contour models and balloons for 2-D and 3-D images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1993, 15(11): 1131-1147. |
| [8] | Xu C Y, Prince J L. Snakes, shapes, and gradient vector flow[J]. IEEE Transaction on Image Processing, 1998, 7(3): 359-369. |
| [9] | Xu C Y, Prince J L. Generalized gradient vector flow external forces for active contours[J]. Signal Processing, 1998, 71(2): 131-139. |
| [10] | 王文哲, 唐克伦, 牟宗魁. 主动轮廓模型综述[J]. 机械设计与制造, 2009(8): 257-259.Wang W Z, Tang K L, Mou Z K. An overview on active contour model[J]. Machinery Design & Manufacture, 2009(8): 257-259. |
| [11] | 陈波, 赖剑煌. 用于图像分割的活动轮廓模型综述[J]. 中国图象图形学报, 2007, 12(1): 11-20.Chen B, Lai J H. Active contour models on image segmentation: A survey[J]. Journal of Image and Graphics, 2007, 12(1): 11-20. |
| [12] | Hilario C, Collado J M, Ma Armingol J, et al. Pedestrian detection for intelligent vehicles based on active contour models and stereo vision[C]//Proceedings of the 10th International Conference on Computer Aided System Theory. Berlin, Germany: Springer, 2005: 537-542. |
| [13] | Zhang F, Zhang X H, Cao K, et al. Contour extraction of gait recognition based on improved GVF Snake model[J]. Computers and Electrical Engineering, 2012, 38(4): 882-900. |
| [14] | Appia V, Yezzi A. Active geodesics: Region-based active contour segmentation with a global edge-based constraint[C]//Proceedings of International Conference on Computer Vision. Piscataway, NJ, USA: IEEE, 2011: 1975-1980. |
| [15] | Shahamatnia E, Ebadzadeh M M. Application of particle swarm optimization and snake model hybrid on medical imaging[C]//Proceedings of International Workshop on Computational Intelligence in Medical Imaging on Paris. Piscataway, NJ, USA: IEEE, 2011: 11-15. |
| [16] | Buch N, Velastin S A, Orwell J. A review of computer vision techniques for the analysis of urban traffic[J]. IEEE Transactions on Intelligent Transportation System, 2011, 12(3): 920-939. |
| [17] | Huang Y P. Obstacle detection in urban traffic using stereovision[C]//Proceedings of Intelligent Transportation Systems. Piscataway, NJ, USA: IEEE, 2005: 357-362. |
| [18] | Yang Y, Yang J Y, Guo D Y. Pedestrian detection on moving vehicle using stereovision and 2D cue[C]//Proceedings of Intelligent Science and Intelligent Data Engineering. Piscataway, NJ, USA: IEEE, 2013: 466-474. |
| [19] | He X C, Yung N H C. Corner detector based on global and local curvature properties[J]. Optical Engineering, 2008, 47(5): 057008. |
| [20] | 朱玉艳, 尚振宏, 康燕妮, 等. 角点检测技术研究及进展[J]. 电脑开发与应用, 2010, 23(3): 40-43.Zhu Y Y, Shang Z H, Kang Y N, et al. Research and progress in corner detection[J]. Computer Development & Applications, 2010, 23(3): 40-43. |



