2. 北京工业大学电子信息与控制工程学院, 北京 100124
2. College of Electronic and Control Engineering, Beijing University of Technology, Beijing 100124, China
1 引言
城市污水处理是解决水污染日益严重、 缓解水资源短缺的一种有效途径,其目的是通过相应的操作手段,使得包括生化需氧量(BOD)、 化学需氧量(COD)、 固体悬浮物(SS)、 氨氮(NH3-N)、 总氮(TN)、 总磷(TP)等在内的出水水质参数达标,这些出水水质参数的可靠、 准确测量是污水处理过程成功实现控制及优化的前提.
目前,大多数的城市污水处理厂采用活性污泥法处理污水[1],其生化反应机理非常复杂,无法直接获得部分关键过程变量与控制变量直接的对应关系. 而BOD、 COD等关键水质参数无法有效实时测量[2],在一定程度上制约着控制优化策略的制定. 因此,如何快速准确地实时测量或估计BOD、 COD的浓度一直是污水处理研究领域的一个关键科学问题.
与传统的仪器仪表测量相比,以人工神经网络为代表的数据驱动软测量技术具有明显的反应快速、 价格低廉、 实现方便等优势,已经在污水处理领域得到了广泛的关注和应用[3, 4, 5, 6, 7, 8, 9, 10, 11]. 通过分析与BOD、 COD等关键水质参数关系密切的其它可测、 易测参量,借助神经网络建模预测技术,实现对BOD、 COD等浓度的预测. Lee等[9]采用基于神经网络的序列建模方法对出水BODeff(t)、 CODeff(t)、 SSeff(t)、 TNeff(t)浓度进行预测,首先,由当前时刻的流速、 入水CODin(t)、 SSin(t)、 TNin(t)及前一时刻的BODin(t-1)浓度预测当前时刻的BODin(t),再结合曝气池内污泥浓度MLSS(t)及前一时刻出水BODeff(t-1)浓度对当前时刻的BODeff(t)浓度进行预测. 该方法尽管能够成功实现关键水质参数的预测,但其序列建模的形式势必引起累积误差以及时间损耗,因而其响应速度及预测精度有待进一步提高. Chen等[10]采用进化灰度动态建模的方法对工业污水处理厂的出水COD、 SS浓度进行预测,获得了优于神经网络建模的预测精度. 然而,两种建模方法选用的输入不尽相同,这也可能是引起不同预测结果的主因. Noori等[11]采用降阶自适应神经—模糊推理系统(RO-ANFIS)、 降阶神经网络(RONN)、 降阶支持向量机(ROSVM)等软测量技术实现BOD的快速估计.
神经网络是对生物神经系统结构和功能的模拟,主要由网络结构和学习算法两部分组成. 多层前馈神经网络(multilayer feedforward neural network,MLFNN)由于结构简单及理论上的任意逼近能力,得到了广大学者的普遍关注. 然而,神经网络的功能是由结构决定的,简单的结构既是网络的优点,同时也制约着网络性能的发挥. 神经网络的设计与优化一直是相关理论及应用研究的热点问题. 为提高网络的学习能力、 求解复杂实际问题的能力,Jaeger等[12]提出回声状态网络(echo state network,ESN),其隐含层神经元之间采用稀疏连接,并且仅对连接输出神经元的权值进行训练和调整,而连接隐含层神经元的权值则是随机生成并保持不变. 当ESN中的神经元类型为尖峰神经元(spiking neurons)时,ESN则等价于流形状态机(liquid state machines)[13, 14]. ESN对于时间序列预测具有非凡的处理能力,然而由于存在误差积累问题,对于含有噪声的实际序列则表现一般. 为解决深层结构相关的优化问题,2006年Hinton等人基于深信度网(deep belief nets)提出一种无监督的贪心逐层训练算法——深度学习(deep learning)[15]. 深度学习在语音识别、 计算机视觉等方面的显著优势引起了大家的广泛关注,然而却无法很好解决虹膜识别等含有单个样本的模式识别问题. 为提高网络的学习能力及泛化能力,根据大脑皮层内神经元的连接模式设计了隐含层内神经元侧向抑制及不相邻层内神经元跨越传输的跨越—侧抑制神经网络(span-lateral inhibition neural network,S-LINN)[16]. 与传统的神经网络相比,S-LINN能够以更为精简的结构获得更为出众的学习能力.
本文旨在研究基于神经网络的BOD智能特征建模方法,以S-LINN软测量为技术手段,设计一种快速高效的权值分类序列学习算法,实现对BOD的可靠、 准确检测.
2 S-LINN及分类序列学习S-LINN是根据结构仿生学原理借鉴大脑皮层神经元的类型及连接模式而设计的一种新型网络. 皮层神经元在皮层内并非随机分布,而是以“层”的形式进行排列,并与不同的皮层区域和子皮层区域相连[17]. 其中,大约70%~80%的新皮层神经元为兴奋的锥体神经元,可以跨越整个皮层厚度,以垂直分布的方式对同一个输入产生响应; 而剩余的20%~30%的神经元为中间神经元,并且绝大多数是抑制的中间神经元[17, 18]. 在新皮层内,同时存在着兴奋的神经回路和抑制的神经回路.
2.1 S-LINN拓扑结构如图 1所示,S-LINN以多层神经网络(包含前馈连接ωji、 ωgj、 ωkg)为基础,模仿锥体神经元在皮层间的跨越传输,在非相邻层之间引入跨越连接(如图中虚线表示的连接ωgi、 ωki、 ωkj); 同时,在同一个隐含层内引入侧向抑制连接(如一端为方框一端为箭头的连接,如vjr、 vgs所示),模拟生物神经网络中的侧抑制机制.
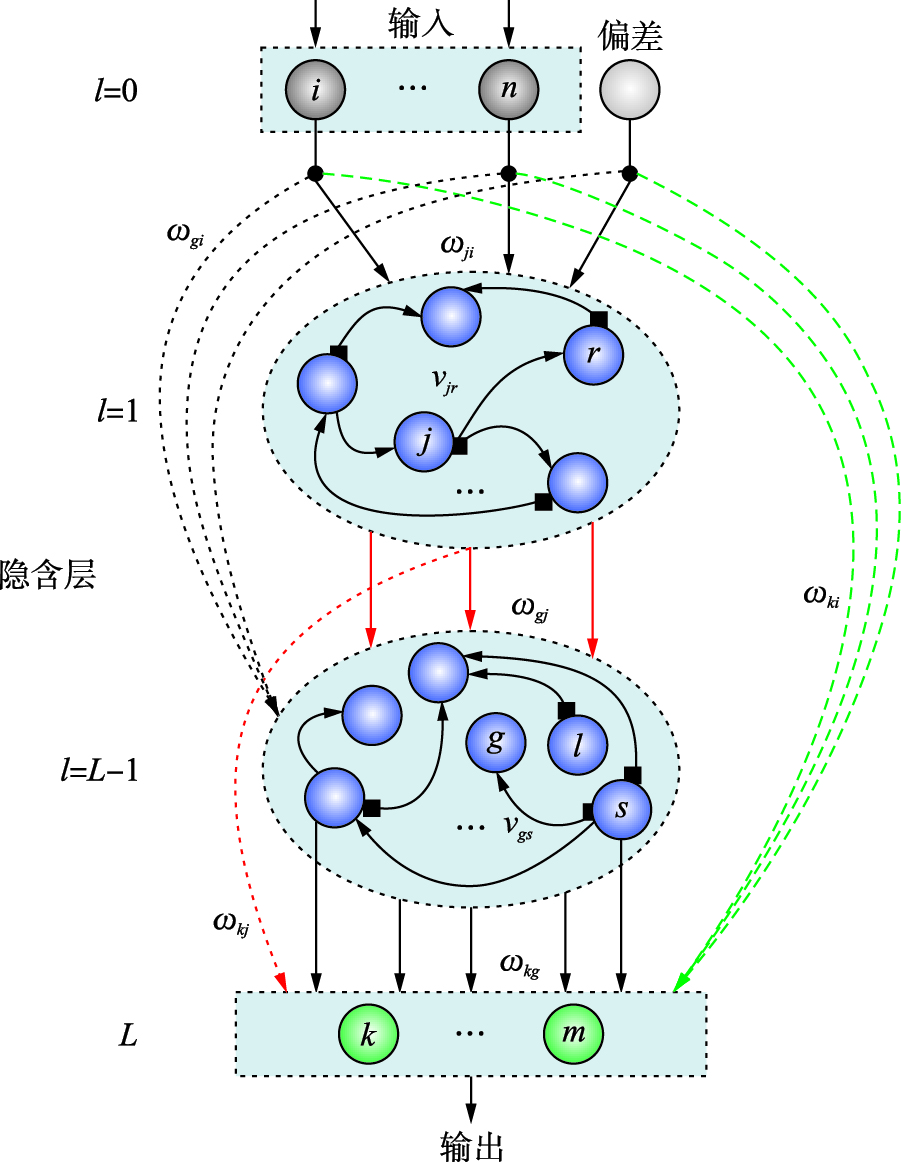 |
| 图 1 S-LINN结构Fig. 1 Architecture of S-LINN |
2.2 S-LINN数学模型
图 1中,l表示神经网络的层,其中l=0表示输入层,l=L表示输出层,l∈[1,L-1]表示隐含层; ω**表示层间的连接权值,ν**表示隐含层内的侧抑制连接权值. 根据图 1所示的网络结构及符号定义,可得S-LINN的数学模型如下:
(1) 输入层
l=0层内应有n个输入神经元对应网络的n维输入,则第i个输入神经元的输出oip0为
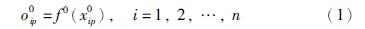

(2) 隐含层
由于S-LINN网络内存在不同层之间信息的前馈及跨越传输,以及隐含层内神经元之间的侧抑制连接机制实现的信息传输和竞争,因此隐含层l内的神经元有两类输入: 一类是来自于[0,l-1]层内神经元的传入输入(afferent input),另一类是来自于同一层内相邻神经元的抑制输入(inhibitory input). 图 1中, vjr和vgs分别表示同一层内神经元r作用于神经元j以及神经元s作用于神经元g的抑制系数,则l层内神经元j的输出ojl为
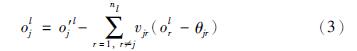
(3) 输出层
在S-LINN中,输出神经元可以接收来自于输入层和隐含层内神经元的输出信号,因此第k个输出神经元的输出ok为

不失一般性,可得L+1层S-LINN网络的数学模型如下:

由于输出ojl是关于输入x的函数,所以o也是x的函数. 显然,S-LINN网络实现了n维空间到m维空间的映射.
2.3 权值分类序列学习方法(1) 问题描述
首先,假设有N组可以用于网络训练的有效样本. 那么,在理论上,若一个L+1层的前馈网络,其l层上有nl个神经元,当隐含层神经元的数量为N,即当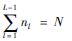 时,该网络能够以零误差逼近这N组样本. 亦即,存在ωki*,ωji*,ωkj*和bl*使得下式成立:
时,该网络能够以零误差逼近这N组样本. 亦即,存在ωki*,ωji*,ωkj*和bl*使得下式成立:
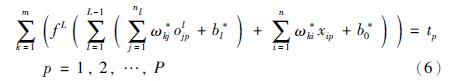
为便于描述,用ωkjl表示连接第k个输出神经元与l层第j个神经元的权值. S-LINN网络的输出神经元是线性的. 因此,上式可改写为如下形式:
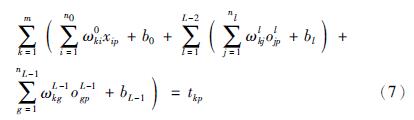
上述P个方程的矩阵表示形式如下:

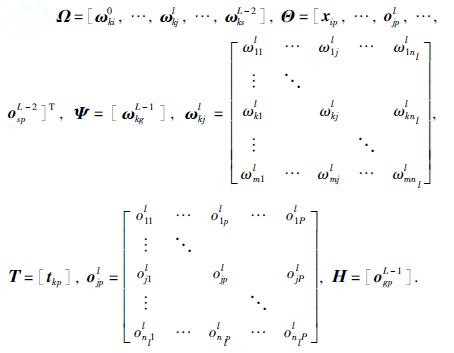
由上述分析可知,S-LINN网络的参数学习过程实际上就是权值Ω和Ψ的组合优化过程. 其中,Ω为所有通过跨越连接(l∈[0,L-1])与输出神经元相连的权值矩阵,而Ψ为最后一个隐含层(l=L-1)与输出层的前馈连接权值矩阵. 由于神经网络的初始权值是在限定的范围内依概率随机生成的,具有足够的任意性和代表性. 同时,研究表明[19]对于含有N个不同实例的有限集,一个具有非线性激励函数的单隐含层前馈网络(SLFN)最多只需要N个隐含层节点就可以无误差地逼近这N个实例,即SLFN的学习能力只与隐含层节点的数目有关,而与输入层的权值无关. 而S-LINN可以认为是一个具有跨越和侧抑制连接的多层前馈网络,与输出神经元通过跨越连接的输入层神经元相当于是前馈网络隐含层神经元的一部分,所以在设计S-LINN的学习算法时,仅学习网络的跨越输出权值和前馈输出权值.
(2) 跨越输出权值学习
在网络开始学习之前,对网络所有权值进行初始化,因此可得网络的初始输出及对应的神经元输出. 式(8)可作如下变形:


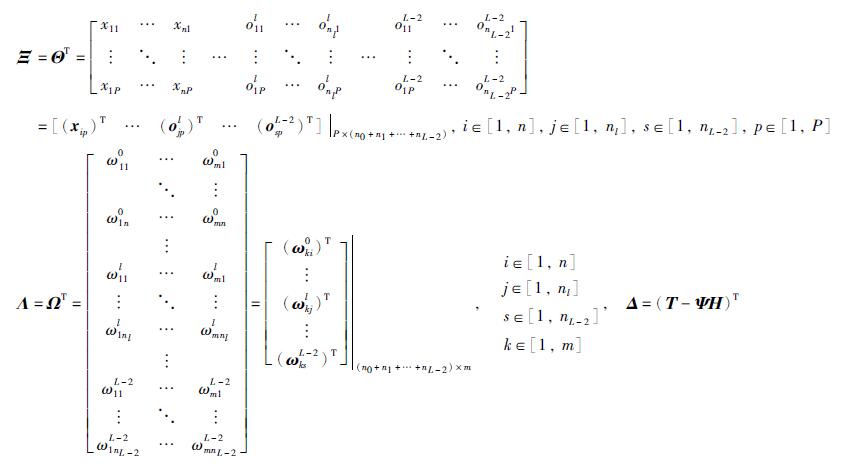
基于网络的初始权值,S-LINN跨越输出权值的训练可以等价于求解线性系统ΞΛ=Δ的最小二乘解Λ*,即:
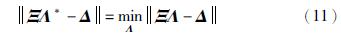
不失一般性,存在矩阵Φ=Ξ ,即Φ为矩阵Ξ的Moore-Penrose广义逆矩阵,并且使得ΦΔ为线性系统ΞΛ=Δ的模最小的最小二乘解. 由此,估计S-LINN的跨越输出权值为
,即Φ为矩阵Ξ的Moore-Penrose广义逆矩阵,并且使得ΦΔ为线性系统ΞΛ=Δ的模最小的最小二乘解. 由此,估计S-LINN的跨越输出权值为

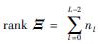
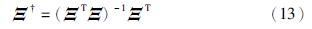
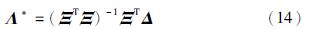
综上所述,S-LINN的跨越输出权值学习过程的关键步骤为快速高效地估计线性系统ΞΛ=Δ的最小二乘解.
(3) 前馈输出权值学习
由于矩阵Ξ可能是非奇异矩阵,所以单一的跨越输出权值训练不能保证S-LINN能够以零误差或任意精度逼近给定的系统. 这就要求对其它权值进行进一步训练,以期发挥网络的最优性能.
研究表明[19],当且仅当前馈网络SLFN的隐含层神经元数量大于等于训练样本的个数P时,网络的隐含层输出矩阵才有可能是奇异的可逆矩阵. 而对于S-LINN网络来说,当含有足够多的隐含层神经元,即:

通常情况下,神经网络隐含层神经元的数量远远小于训练样本的个数,即对于S-LINN网络有:


从功能扩展的角度出发,神经网络隐含层神经元的输出可以看作是网络函数空间上的一个基,而最后一个隐含层神经元的输出仅是这些基函数使用的一个子集而已. 这就意味着,越接近输出层的隐含层神经元对于网络的贡献越大. 因此,它们与输出神经元的连接权值的学习尤为重要. 即在第一步学习的基础上,训练Ψ*和Λ*的最优组合,使得下述代价函数J最小:
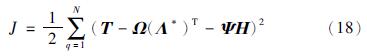
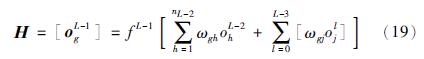
为了提高前馈输出权值训练的可操作性及分步训练策略的适用性,连接L-2层到L-1层的前馈连接权值ωgh也作为隐含层输出权值的一部分进行训练. 因此,在第2步的学习中共有ωgh和ωkgL-1两组权值需要进行训练. 这两组权值的学习过程,可以看作是隐含层具有侧抑制连接的3层网络,因而,很多适用于训练3层前馈网络的学习算法经过改进后都可以用来训练S-LINN前馈输出的权值. 不失一般性,本文设计一种基于梯度下降的迭代学习算法用于S-LINN前馈输出权值的训练:
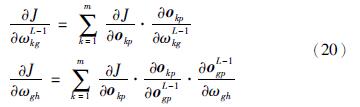
综上所述,基于跨越输出权值和前馈输出权值分类训练的序列学习方法主要有以下几个步骤:
Step 1: 初始化. 首先,根据学习样本的维数确定网络输入层和输出层神经元的数量; 其次,根据问题的难易程度设定合适的网络隐含层的层数及隐含层神经元数量; 最后,对网络权值进行随机初始化赋值.
Step 2: 估计跨越输出权值. 借助初始化的随机权值,根据学习样本,采用最小二乘方法对跨越输出权值Λ进行估计.
Step 3:学习前馈输出权值. 根据跨越输出权值及其它初始化权值,进行前馈输出权值Ψ的学习. 根据本文设计的梯度下降学习算法,依据链式法则,根据式(20)进行迭代学习.
Step 4: 判断网络性能: 当学习满足终止条件时,停止训练,输出网络; 否则,重复运行Step 3.
3 S-LINN序列学习BOD特征建模基于S-LINN的污水处理关键水质参数BOD的智能特征建模是通过对活性污泥法污水处理过程的分析,从众多的可测变量中分析并选取与BOD关系密切且较易测得的参量作为神经网络特征建模系统的辅助变量,即网络输入,经过S-LINN(由历史数据训练好的网络)的计算,实现对BOD的实时预测. 基于S-LINN的关键水质参数智能特征建模流程及其与污水处理控制系统的关系如图 2所示.
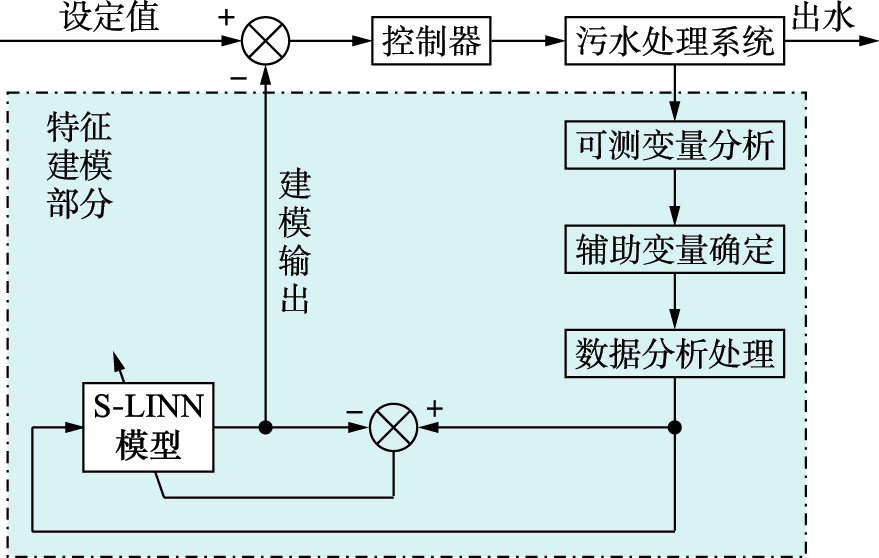 |
| 图 2 基于S-LINN污水处理智能特征建模结构框图Fig. 2 Block diagram of wastewater treatment intelligent characteristic modelling based on S-LINN |
基于S-LINN的智能特征建模包括变量的分析、 辅助变量的确定、 神经网络设计等几个部分. 根据实际的污水处理过程可知,可以测得的辅助变量主要有: 入水流量Qin、 酸碱度(PH)、 SS浓度、 钙离子(Ca2+)浓度、 COD浓度、 氧化还原电位(ORP)、 MLSS浓度、 溶解氧浓度DO、 NH3-N浓度、 NO2-N浓度、 NO3-N浓度、 CN-浓度、 Cr6+浓度、 Ar-OH浓度、 AS浓度及温度等,其中,可能对BOD的浓度产生影响的主要变量为Qin、 PH、 SS、 COD、 DO、 ORP、 MLSS及温度等. 本文选取北京市某污水处理厂水质检测日报表数据进行BOD预测仿真研究. 由于该污水处理厂运行平稳,入水流量波动较小,因而对出水水质的影响可以忽略. 根据采集的有效数据,采用主元分析(PCA)方法[20]确定对BOD产生影响的主要变量,从而得到预测BOD浓度的特征参量主要有PH、 DO、 出水SS及COD浓度. 因而,本文选取PH、 DO、 出水SS和COD作为S-LINN的输入变量,而输出变量则为预测的出水BOD浓度.
4 仿真实验研究本文所做实验仿真研究均是基于Matlab 7.11在Intel®CoreTM 2 Duo CPU 3 GHz,内存1.98 GB的PC机上进行. 为便于比较S-LINN的学习性能,首先选取与BOD特征建模预测类似的洛伦兹混沌时间序列预测基准问题进行验证.
4.1 洛伦兹混沌时间序列预测问题混沌时间序列预测是检验神经网络结构和方法的基准问题[21, 22, 23]. 洛伦兹吸引子是下列常微分方程(ODE)[24]的一个解:
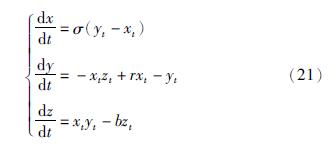
为便于比较,本文选取σ=10,r=28,b=8/3. 借助Matlab的ode45命令求解式(21)所示的微分方程,采样时间Ts=0.01 s得到方程在x维度上的混沌时间序列x(t). 设定嵌入维数d=3,嵌入延迟Δ=4构造预测系统[25]:
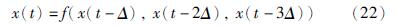
为了降低过渡阶段对时间序列的影响,选取30 s~45 s内生成的1 500组数据作为训练样本训练S-LINN,接下来的45 s~55 s内生成的1 000组数据作为测试样本评价网络的泛化能力. 评价网络的性能指标为归一化的均方误差(NMSE)[26]:
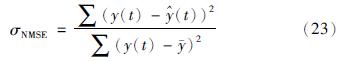
 (t)、 y 分别为观测值、 预测值及观测值的均值.
(t)、 y 分别为观测值、 预测值及观测值的均值.
本次实验选用含有5个隐含层神经元的S-LINN进行该时间序列的预测. 训练样本和测试样本的期望输出(观测值,“*”表示)和网络实际输出(预测值,“o”表示)及各个样本所对应的误差如图 3(a)和图 3(b)所示. 由图 3可知,采用S-LINN进行洛伦兹混沌时间序列的预测时,能够获得较高的精度,样本误差限定在一个小范围内(±1e-5).
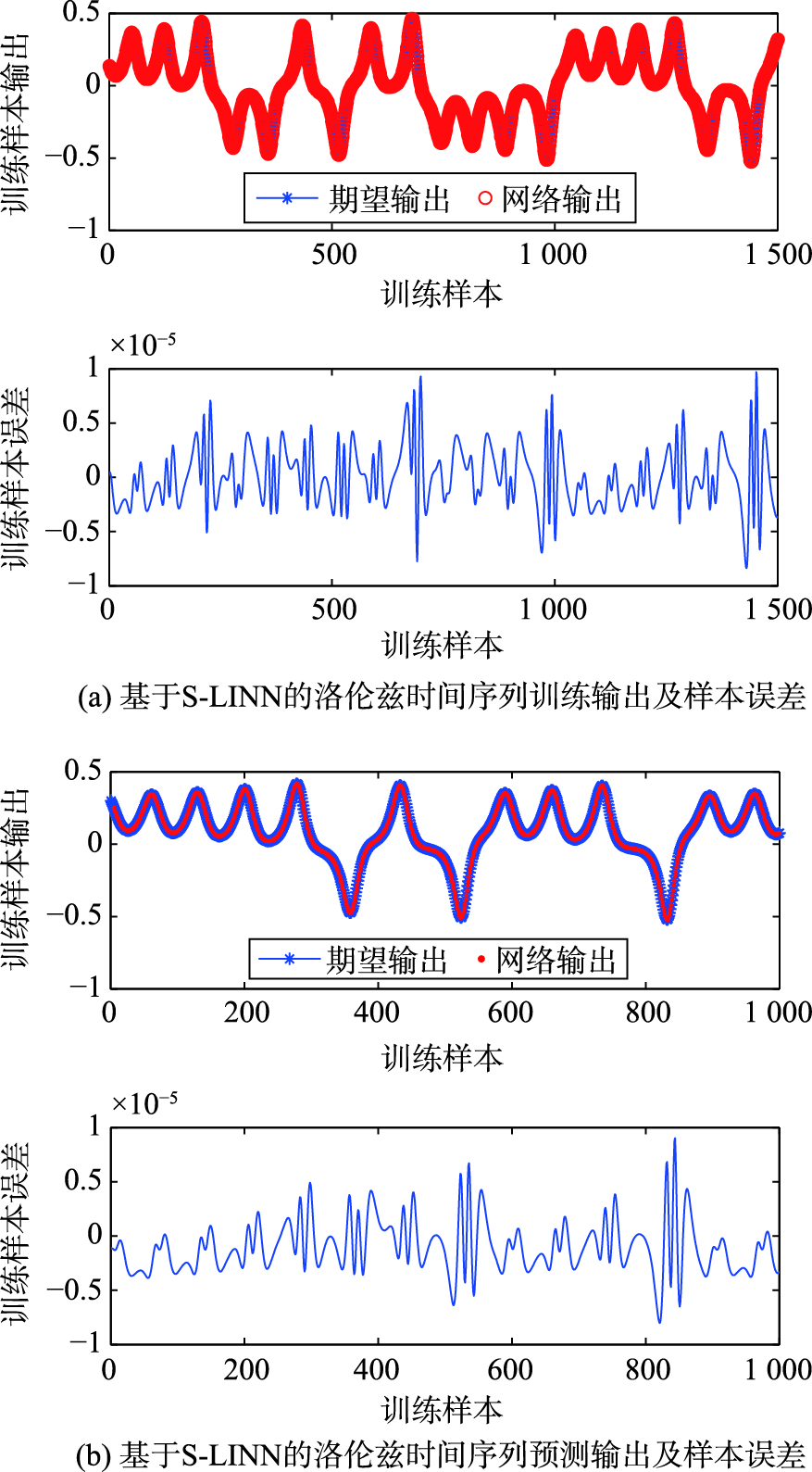 |
| 图 3 基于S-LINN的洛伦兹时间序列预测结果及样本误差Fig. 3 The forecasting results and sample errors of Lorenz time-series based on S-LINN |
S-LINN与径向基函数(radial basis function,RBF)、 多层感知器(multilayer perceptron,MLP)等神经网络方法进行洛伦兹混沌时间序列预测的性能对比如表 1所示. 由表中数据可知,S-LINN能够以较小的网络结构,获得最优的处理效果: 5个隐含层神经元,训练误差σtr=4.39e-13,测试误差σte=6.65e-13,远远优于其它几种方法获得的精度. 这充分说明基于SFSL的S-LINN方法在处理此类时间序列预测问题时具有较好的学习性能.
由于选取PH、 DO、 出水SS和COD作为S-LINN的输入变量对出水BOD进行预测,输入和输出神经元数量分别为4和1. 数据选自某污水处理厂水质检测日报表,共200组有效数据可以用于S-LINN的训练和测试,如图 4所示. 样本数据归一化到[0, 1],设置网络的期望学习均方误差MSE为1e-5.
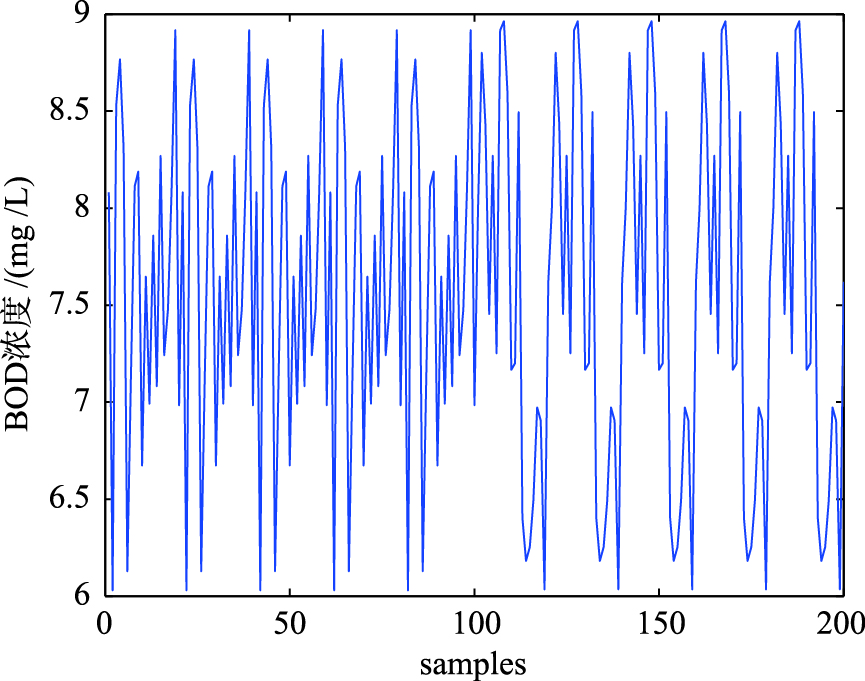 |
| 图 4 BOD建模样本数据Fig. 4 The samples for BOD modelling |
实验1 选取前100组数据作为训练样本进行S-LINN的训练,剩余的100组样本进行网络性能测试.
在此实验中,引入平均绝对百分比误差(MAPE)衡量网络的学习性能:
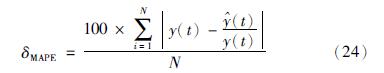
 (t)分别为系统的观测值和估计值, N为样本的个数.
(t)分别为系统的观测值和估计值, N为样本的个数.
如图 5(a)所示为网络的训练样本,其中“o”表示样本的期望输出,“*”表示网络的实际输出(下同),图 5(b)所示为训练样本的学习误差. 图 6所示为均方误差εMSE表示的S-LINN的学习误差曲线. 由实验结果可知,S-LINN对训练样本的学习具有非常高的精度,其训练误差εtr可以达到1.284e-6,误差的最大值和最小值分别为8.176 1e-3(第1组样本)和2.575 7e-5(第8组样本). 此时,S-LINN能够很好地学习训练样本,平均绝对百分比训练误差δtr达到5.00e-5%. 然而,网络的泛化能力却很弱,平均绝对百分比测试误差δte仅为0.461 7%,基本无法实现对BOD的准确预测.
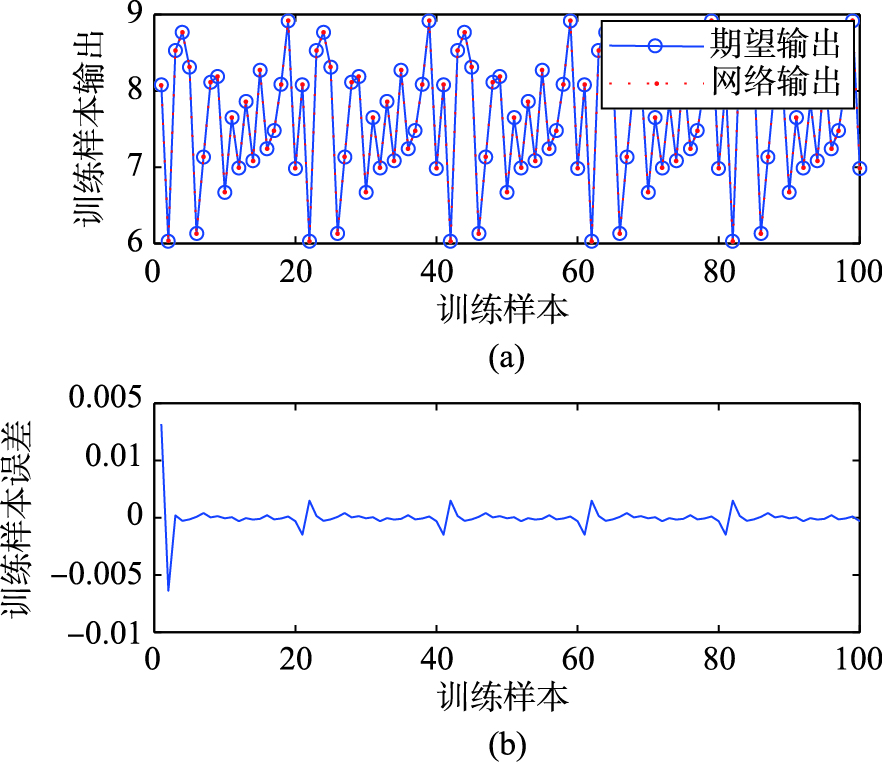 |
| 图 5 基于前100组样本的S-LINN训练输出及样本误差Fig. 5 The training outputs and the corresponding sample errors of S-LINN based on the first 100 samples |
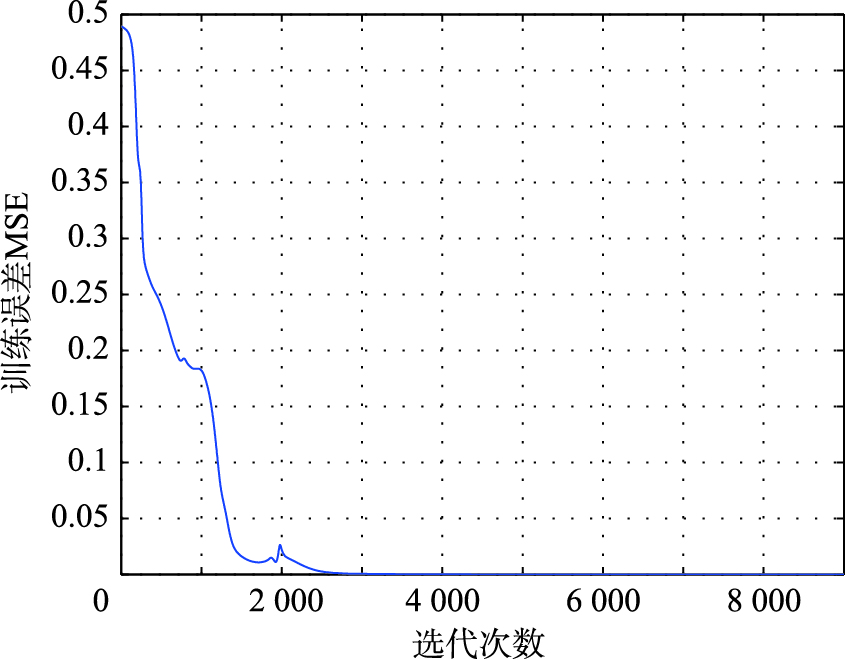 |
| 图 6 基于顺序选取样本的BOD预测学习误差曲线Fig. 6 The learning error curve of BOD forecasting based on the sample′s sequential selection |
实验1表明,S-LINN在解决此类实际问题时,尽管能够获得非常高的学习精度,但由于网络的泛化能力较弱,无法实现特征建模的目的.
观察图 4所示的样本可知: 前100组样本与后100组样本具有明显不同的周期性. 因此,为避免周期性样本对网络学习能力的影响,独立进行实验2.
实验2 从200组有效样本中随机选取100组用于网络训练,而剩余的100组样本进行网络性能测试.
图 7(a)为随机选取训练样本时S-LINN的网络训练输出,图 7(b)为训练样本对应的学习误差;图 8(a)为剩余样本基于S-LINN的预测输出,图 8(b)为测试样本对应的预测误差; 图 9所示为实验2基于随机样本的学习误差曲线. 其中,网络的学习精度的训练误差εtr=9.265 7e-3,而测试精度误差εte=1.71e-2; 训练样本的平均绝对百分比误差εtr=0.006 8%,而测试样本的平均百分比误差为εte=0.012 6%.
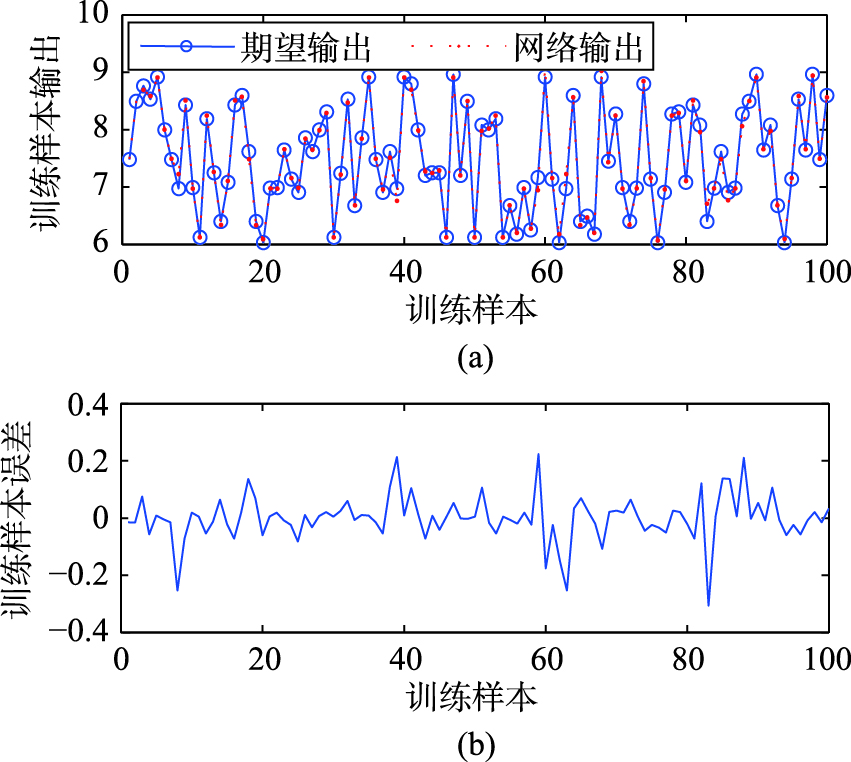 |
| 图 7 基于随机样本的S-LINN训练输出及样本误差Fig. 7The training outputs and the corresponding sample errors of S-LINN based on the sample′s random selection |
 |
| 图 8 基于随机样本的S-LINN预测输出及样本误差Fig. 8 The forecasting outputs and the corresponding sample errors of S-LINN based on the sample′s random selection |
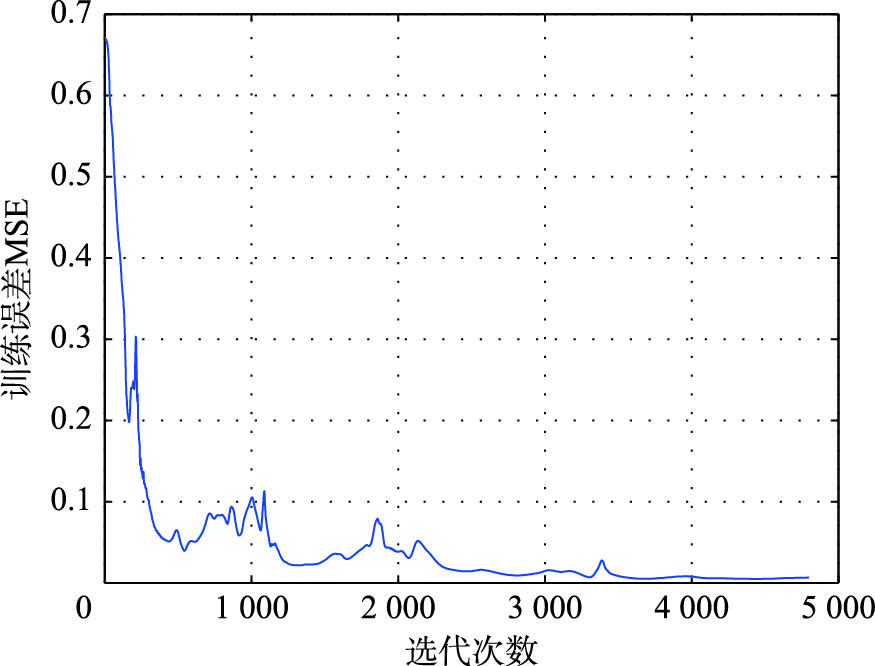 |
| 图 9 基于随机样本的BOD预测学习误差曲线Fig. 9 The learning error curve of BOD forecasting based on the sample′s random selection |
由实验2可知,基于S-LINN的BOD特征建模可以将训练误差控制在[-0.2 mg/L,0.2 mg/L]之间,而测试误差控制在[-0.5 mg/L,0.5 mg/L]之间. 说明随机选取样本进行网络的训练和测试时,能够实现对BOD的准确预测.
5 结论针对污水处理关键水质参数BOD的实时预测问题,根据跨越—侧抑制神经网络(S-LINN)的权值连接特点设计了权值分类序列学习方法,并进行BOD的特征建模研究.S-LINN是根据大脑皮层内神经元连接模式设计的,具有跨越和侧抑制连接; 根据网络的连接特性将跨越输出权值和前馈输出权值分别训练、 序列学习. 实验研究表明,该网络与其它神经网络相比在学习精度和泛化能力方面有一定程度的提高. 通过对污水处理过程中BOD及其相关参数的分析设计了S-LINN的BOD特征建模方法,实现了对BOD的有效实时预测. 同时,基于S-LINN的学习能力,该方法对于其它系统的特征建模及参数预测也具有一定的借鉴意义. 然而,该学习策略以及基于此的自组织学习方法仍是下一步研究重心.
| [1] | Olsson G. Instrumentation, control and automation in the water industry-state-of-the-art and new challenges[J]. Water Science & Technology, 2006, 53(4/5):1-16. |
| [2] | Zhu J B, Zurcher J, Rao M, et al. An on-line wastewater quality predication system based on a time-delay neural network[J]. Engineering Applications of Artificial Intelligence, 1998, 11(6):747-758. |
| [3] | Khataee A R, Kasiri M B. Modeling of biological water and wastewater treatment processes using artificial neural networks[J]. Clean-Soil, Air, Water, 2011, 39(8):742-749. |
| [4] | Haimi H, Mulas M, Corona F, et al. Data-derived soft-sensors for biological wastewater treatment plants:An overview[J]. Environmental Modelling & Software, 2013, 47:88-107. |
| [5] | Hamed M M, Khalafallah M G, Hassanien E A. Prediction of wastewater treatment plant performance using artificial neural networks[J]. Environmental Modelling & Software, 2004, 19(10):919-928. |
| [6] | Ráduly B, Gernaey K V, Capodaglio A G, et al. Artificial neural networks for rapid WWTP performance evaluation:Methodology and case study[J]. Environmental Modelling & Software, 2007, 22(8):1208-1216. |
| [7] | 丛秋梅, 苑明哲, 王宏, 等. 基于元学习的污水水质集成软测量模型[J]. 信息与控制, 2014, 43(2):248-252. Cong Q M, Yuan M Z, Wang H, et al. Soft-sensor of water quality based on integrated EML with meta-learning[J]. Information and Control, 2014, 43(2):248-252. |
| [8] | Emamgholizadeh S, Kashi H, Marofpoor I, et al. Prediction of water quality parameters of Karoon River (Iran) by artificial intelligence-based models[J]. International Journal of Environmental Science and Technology, 2014, 11(3):645-656. |
| [9] | Lee J W, Suh C, Hong Y S, et al. Sequential modelling of a full-scale wastewater treatment plant using an artificial neural network[J]. Bioprocess and Biosystems Engineering, 2011, 34(8):963-973. |
| [10] | Chen H W, Yu R F, Ning S K, et al. Forecasting effluent quality of an industry wastewater treatment plant by evolutionary grey dynamic model[J]. Resources, Conservation and Recycling, 2010, 54(4):235-241. |
| [11] | Noori R, Safavi S, Nateghi S A. A reduced-order adaptive neuro-fuzzy inference system model as a software sensor for rapid estimation of five-day biochemical oxygen demand[J]. Journal of Hydrology, 2013, 495(1):175-185. |
| [12] | Jaeger H, Haas H. Harnessing nonlinearity:Predicting chaotic systems and saving energy in wireless communication[J]. Science, 2004, 304(5667):78-80. |
| [13] | Maass W, Natschläger T, Markram H. Real-time computing without stable states:A new framework for neural computation based on perturbations[J]. Neural Computation, 2002, 14(11):2531-2560. |
| [14] | Maass W, Markram H. On the computational power of circuits of spiking neurons[J]. Journal of Computer and System Sciences, 2004, 69(4):593-616. |
| [15] | Hinton G E, Osindero S, Teh Y. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7):1527-1554. |
| [16] | 杨刚, 乔俊飞, 薄迎春, 等. 一种基于大脑皮层结构的侧抑制神经网络[J]. 控制与决策, 2013, 28(11):1702-1706. Yang G, Qiao J F, Bo Y C, et al. A novel lateral inhibition neural network based on neocortex topology[J]. Control and Decision, 2013, 28(11):1702-1706. |
| [17] | De Felipe J, Farinas I. The pyramidal neuron of the cerebral cortex:Morphological and chemical characteristics of the synaptic inputs[J]. Progress in Neurobiology, 1992, 39(6):563-607. |
| [18] | Markram H, Toledo-Rodriguez M, Wang Y, et al. Interneurons of the neocortical inhibitory system[J]. Nature Reviews Neuroscience, 2004, 5(10):793-807. |
| [19] | Huang G B, Babri H A. Upper bounds on the number of hidden neurons in feedforward networks with arbitrary bounded nonlinear activation functions[J]. IEEE Transactions on Neural Networks, 1998, 9(1):224-229. |
| [20] | Gernaey K V, van Loosdrecht M C M, Henze M, et al. Activated sludge wastewater treatment plant modelling and simulation:State of the art[J]. Environmental Modelling and Artificial Intelligence, 2004, 19(9):763-783. |
| [21] | Gholipour A, Araabi B N, Lucas C. Predicting chaotic time series using neural and neurofuzzy models:A comparative study[J]. Neural Processing Letters, 2006, 24(3):217-239. |
| [22] | Inoussa G, Peng H, Wu J. Nonlinear time series modeling and prediction using functional weights wavelet neural network-based state-dependent AR model[J]. Neurocomputing, 2012, 86(1):59-74. |
| [23] | Gan M, Peng H, Peng X Y, et al. A locally linear RBF network-based state-dependent AR model for nonlinear time series modeling[J]. Information Sciences, 2010, 180(22):4370-4383. |
| [24] | Lorenz E N. Deterministic nonperiodic flow[J]. Journal of the Atmospheric Sciences, 1963, 20(2): 130-141. |
| [25] | Dudul S V. Prediction of a Lorenz chaotic attractor using two-layer perceptron neural network[J]. Applied Soft Computing, 2005, 5(4): 333-355. |
| [26] | Ardalani-Farsa M, Zolfaghari S. Chaotic time series prediction with residual analysis method using hybrid Elman-NARX neural networks[J]. Neurocomputing, 2010, 73(13/14/15): 2540-2553. |



