2. 东南大学复杂工程系统测量与控制教育部重点实验室, 江苏南京 210096
2. Key Laboratory of Measurement and Control of Complex Systems of Engineering of Ministry of Education, Southeast University, Nanjing 210096, China
1 引言
步进电机作为许多精密仪器的执行对象,具有行程距离大、 运动分辨率高、 输出力矩大等特点,是一种将电脉冲信号转化为角位移或直线位移的执行元件.由于其位移量与输入脉冲严格成正比且单步偏差不会影响到下一步精度,因此步距误差不会累积.相比一般的电机,步进电机无需利用位置传感器或速度传感器进行闭环控制即可得到精确的位置定位,因此在各类精密控制领域中得到了广泛应用.
虽然步进电机本身具有很多优势,但其控制性能很大程度上取决于驱动技术,不同的驱动方式对于步进电机运动影响很大,主要存在的问题是步进电机在低频运行时的振动、 噪声及高频运行时的过冲、 失步等. 目前,广为采用的有效方式为恒流细分驱动控制[1, 2, 3, 4, 5, 6].
文[7, 8, 9]采用控制器与专用驱动芯片的组合结构,这种方式适用于一般位置控制系统且结构简单,但难以适用于高精密的控制对象; 文[10, 11]在控制器内部实现了基于PI(proportional-integral)电流闭环的细分驱动,即ADC(analoy-to-digital converter)软件恒流方案,理论上可以得到更好的控制效果,但对于不同的控制对象,PI参数的选择可能不一样,因此可能需要复杂的自适应算法; 文[12, 13, 14, 15]实现了基于FPGA的细分驱动控制,即DAC(digital-to analoy converter)硬件恒流措施,该方式利用Bang-Bang控制理论,可以满足系统的快速响应,但控制效果取决于比较器及驱动电路的开关频率,若H桥驱动的开关频率低,该方式的控制效果将会不理想,电流控制会出现振荡,因此利用一般的控制方式难以实现步进电机的高精密控制.
由于FPGA的并行处理能力[16],基于FPGA处理器构建的步进电机系统扩展方便且可移植性高,因此在多轴伺服系统的工业领域得以广泛使用[17, 18, 19, 20]. 而ADC软件恒流控制算法复杂,不适宜在FPGA内实现. 因此,本文采用FPGA与DAC硬件恒流细分驱动相结合的控制思想. 首先,对一般的细分控制理论进行分析,采用恒频斩波与电流快、 慢衰减相结合的方式,提出步进电机电流优化控制策略; 然后,具体设计并实现基于FPGA的高精度细分控制; 最后,将其应用于生物研究中的三轴高精密微型操作仪,并获得了较好的控制效果.
2 步进电机电流优化控制策略恒流细分技术主要用于步进电机位置的精密控制,其基本思想是控制步进电机每相绕组电流的波形,使其阶梯地上升或下降,电流除了获得零值和最大值,还可获得多个稳定的中间状态,使得步进电机的转子旋转步数增多、 步距角减小. 传统理论中,通过在两相混合式步进电机的绕组A、 B中分别通以幅值按正弦规律变化、相位相差90°的均匀阶梯波电流,就可以得到幅度恒定、角度均匀的电流合成矢量,且阶梯越小,所得到的步距角也越小,从而可获得更高的控制精度.
由于步进电机线圈为感性负载,电压与电流呈非线性关系,在开环控制下,无法直接控制电流以满足正弦波的要求,因此需要采用闭环控制使得绕组的实际电流值能较好地跟随给定的正弦波参考电流值. 一般的电流控制策略可满足控制要求,但在高精密控制中,存在着一定弊端:
(1) 电流闭环的实现由硬件决定,因此控制周期直接取决于芯片的最大工作频率,若不对控制频率进行限制,驱动芯片将会严重发热,持续的动作会导致功率管的开关损耗. 另外,频率的突变也容易在绕组中产生很大的浪涌电压.
(2) 电流的调节由中PWM1和PWM2的输出决定,当绕组电流过大时,通过H上桥或H下桥形成续流回路,由绕组本身内阻R消耗电流能量. 这种方式在步进电机低速运行时有一定优势,可以实现较低纹波的电流控制,但是当电机运行速度较快时,仅通过绕组进行电流衰减,会由于响应较慢而达不到设定的期望电流,即存在一定稳态误差,导致控制精度降低.
因此,需要对传统的硬件恒流驱动方式进行改进. 本文采用基于FPGA的DAC硬件恒流细分驱动方式实现电流的闭环控制,如图 1所示.
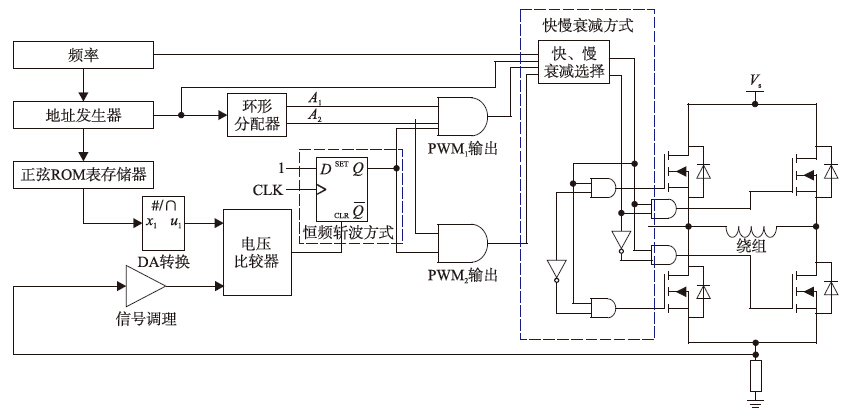 |
| 图 1 步进电机电流优化控制策略Fig. 1 Optimized current control strategy for stepper motor |
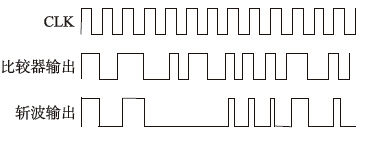 |
| 图 2 恒流斩波原理Fig. 2 Principle of constant frequency chopper |
针对问题(2),当进行电流调节时可根据步进电机运行速度的快慢,进行不同续流回路的电流衰减,以达到在高速状态时电流变化的快速响应,如图 1中的模块(2).
当绕组电流需要增大时,左桥臂与右桥臂功率MOS管交叉导通,绕组导通状态如图 3所示. 当实际电流大于期望电流,此时PWM控制信号将会使MOS管关断,通过绕组电感消耗回路能量. 根据MOS管开、 关的不同,存在着两种续流回路.
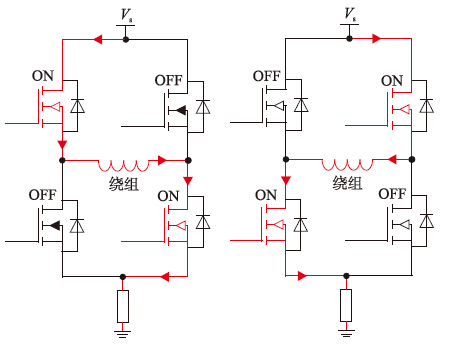 |
| 图 3 线圈绕组通电状态 Fig. 3 Energized state of coil winding |
图 4所示为一种续流方式,可以为上桥或下桥续流. 这种方式通过绕组本身的LR特性耗能,电流衰减缓慢. 当步进电机在低速运行时,通过此方式可以获得较低的纹波电流,然而当步进电机高速运行时,期望电流变化较快,仅通过绕组LR的耗能,实际电流跟不上随期望值的变化,获得的电流将会与期望值存在一定的偏差,导致细分控制效果不理想.
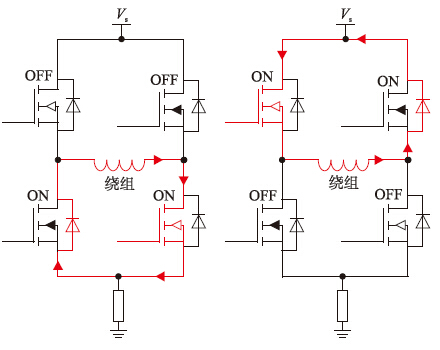 |
| 图 4 电流慢衰减续流方式Fig. 4 Freewheeling of slow decay mode |
图 5所示为另一种续流方式,此时H桥的4个MOS管均关断,绕组电流通过两个反向二极管经电源回路形成续流,绕组两端的电压为Vs+2Vd,其中Vs为控制回路电压,Vd为二极管压降. 在这种方式下电流可以迅速衰减,克服了慢衰减续流在电机高速运行时响应慢的劣势. 不过由于快衰减方式对电流的变化响应快,因此在电机速度较低时,容易造成较大的电流纹波,在一定程度上也会影响控制精度.
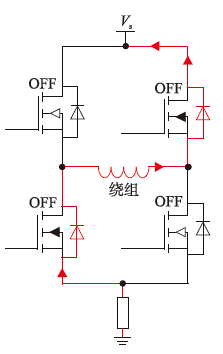 |
| 图 5 电流快衰减续流方式 Fig. 5 Freewheeling of fast decay mode |
基于上述两种续流回路的分析,本文采用恒频斩波与电流快、 慢衰减相结合的优化控制策略,以FPGA为核心控制器实现步进电机的恒流驱动. 电流的快、 慢衰减控制方式由图 6所示曲线决定,其中f为步进电机脉冲控制频率,T为步进电机在绕组电流衰减时快衰减模式所占的时间比例,fL为单纯慢衰减模式脉冲信号频率点,fH为单纯快衰减模式脉冲信号频率点,曲线1、 2分别为两种不同的混合衰减控制曲线,具体的参数选择由步进电机负载特性决定.
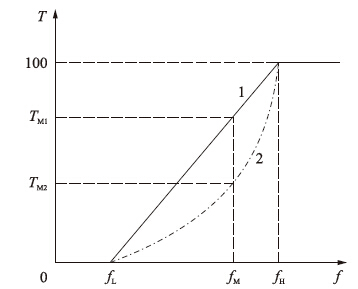 |
| 图 6 电流快、 慢混合衰减选择时间比与控制频率关系图 Fig. 6 Relation between time scale of the choice for fast and slow mixed current decay mode and control frequency |
步进电机运行的最高分辨率由细分数决定,在精密伺 服控制领域中,为了实现更高的分辨率,常要求细分数达128以上,而细分数又决定了正弦参考信号的数据深度. 本文中,细分驱动的电流期望值由存放在FPGA内ROM表实现. 当细分数为256时,对于单相绕组电流ROM表深度为1 024.
另外,需要考虑数据位宽的设定,过小的数据位宽在数据离散化时可能会导致两相参考电压值不变. 数据位宽越大,电压的变化精度越高,也就更有利于数据的离散化,对于细分控制效果越好,如图 7所示. 但是,大数据位宽需要更多的存储容量,同时也需要外部DAC转换芯片拥有更高的分辨率,增加了设计成本. 因此,需要结合数据的深度综合考虑,本文采用12位分辨率位宽实现256细分.
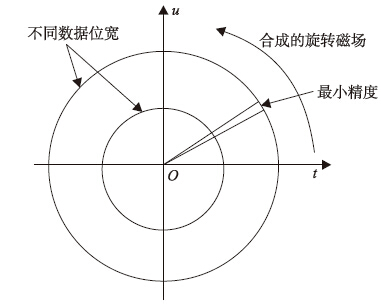 |
| 图 7 数据位宽与精度关系图Fig. 7 Diagram of relationship between data width and precision |
具体实现时,采用Quartus II中提供的LPM定制功能,通过设定ROM表的数据深度及位宽,将相应的正弦全波数据导入.mif文件,初始化文件数据的获取可以通过MATLAB离线方式得到.
3.2 环形脉冲分配环形脉冲分配的作用是产生正弦波信号的同步值,因为由采样电阻反馈的电压信号为正弦全波,仅通过与电压比较器的输出无法控制绕组电流的正向还是反向. 以A相绕组为例,当正弦波相位在0°~180°时,环形脉冲分配器的输出信号ZA和FA分别为1和0,此时控制H桥1、 4号MOS管导通; 当相位在180°~360°时,输出信号分别为0和1,控制H桥2、 3号MOS管导通. 在FPGA内实现时,可直接通过正弦数据表地址进行相位判断.
3.3 H桥PWM斩波信号的产生H桥功率驱动电路采用L6205实现,当使能信号为低时,所有功率MOS管关断; 当使能信号为高时,OUT1的输出由左桥臂控制信号IN1决定,OUT2的输出由右桥臂控制信号IN2决定,且不会产生上、 下桥直通的情况.
当步进电机低速运行时,电流调节用慢衰减方式,部分原理的RTL级实现如图 8所示.
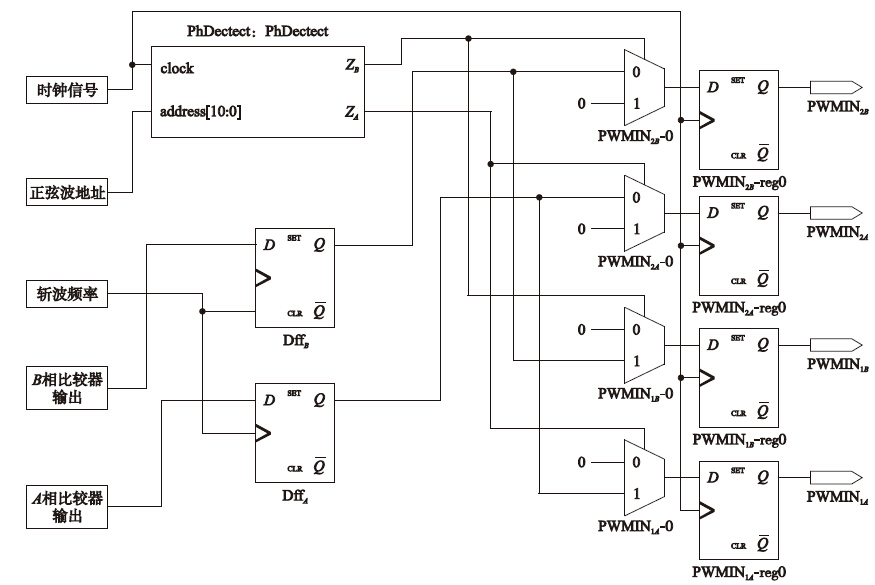 |
| 图 8 恒频斩波、 电流慢衰减模式下的RTL级实现Fig. 8 TL implementation of constant frequency chopper and current slow decay mode |
以A相绕组为例,当绕组电流较大时,比较器输出低电平,此时异步触发器DffA输出立刻置低,若正弦波数据地址在0~511之间,即绕组正向导通,AZ为1,PWMIN2A输出一直为0,PWMIN1A此时输出为0,即H桥上桥关断,进入下桥的慢衰减续流模式,电流减小. 当绕组电流较小时,比较器输出为高电平,此时异步触发器DffA等待斩波频率fs的上升沿到来,当满足条件时,PWMIN2A输出1,H桥1、 4号MOS管导通,电流增大,实现电流的闭环控制. 慢衰减模式下控制信号真值表如表 1所示.
| ROM表地址 | 正弦波符号 | 电流反馈信号 | EN | IN1 | IN2 |
| 0~511 | 正 | 高 | 1 | 0 | 0 |
| 低 | 1 | 1 | 0 | ||
| 512~1 023 | 负 | 高 | 1 | 0 | 0 |
| 低 | 1 | 0 | 1 |
当步进电机高速运行时,电流在减小时的调节方式采用快衰减模式. 以绕组正向导通为例,正弦波地址在256~511之间时,若电流反馈较大,此时关闭EN控制信号,电流通过2、 3号MOS管反向并联的二极管形成续流回路,可以达到快速响应的目的. 快衰减模式下控制信号真值表如表 2所示.
| ROM表地址 | 正弦波符号 | 电流反馈信号 | EN | IN1 | IN2 |
| 0~255 | 正 | 高 | 1 | 0 | 0 |
| 低 | 1 | 1 | 0 | ||
| 256~511 | 正 | 高 | 1 | × | × |
| 低 | 1 | 1 | 0 | ||
| 512~767 | 负 | 高 | 1 | 0 | 0 |
| 低 | 1 | 0 | 1 | ||
| 768~1023 | 负 | 高 | 0 | × | × |
| 低 | 1 | 0 | 1 |
注: ×表示1或0.
由采样电阻反馈的步进电机绕组电流实际为基波频率为fs、 包络为正弦全波的斩波信号,需要对其进行滤波处理以恢复出理想的反馈电流值. 如图 9所示,f(t)为实际绕组电流,fs(t)为斩波后的电流信号,s(t)为抽样信号,通过低通滤波器,无失真恢复出信号f′(t).
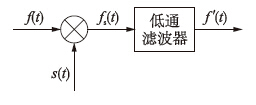 |
| 图 9 绕组电流的滤波与恢复原理Fig. 9 Filtering and recovery principle of winding current |
由于抽样信号频谱是原信号频谱的周期性延拓,设Bf为实际绕组电流信号占有频带宽度,当满足fs≥2Bf时,通过一个截止频率为fc的低通滤波器,则可恢复出原信号. 以正弦波为例,此时有fm≤fc≤fs-fm,其中fm是原信号频谱中的最高频率. 若fs><2Bf,则fs(t)的频谱将出现混迭,此时无法通过低通滤波器获得原信号. 图 10为正弦波抽样后的信号频谱.
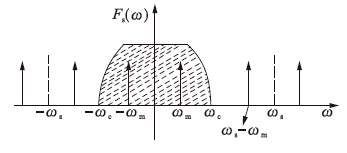 |
| 图 10 正弦波抽样后的信号频谱 Fig. 10 Signal spectrum after sampling a sine wave |
对于正弦全波,其频谱特征为正弦波频率的偶次谐波. 若以2fm为基波,当大于3次谐波时,频谱几乎可以忽略,因此,低通滤波器截止频率fc应满足:
4 实验结果图 11为搭建的生物研究中某型号高精密微型操作仪的测试平台,采样三轴联动控制结构,拟实现的控制精度为: X、 Y、 Z三轴的最高步进精度50 nm,可重复控制精度1 μm,三轴最大行程15 mm,无自主性漂移.
 |
| 图 11 高精密微型操作仪测试平台Fig. 11 Test bench of high precision micro-manipulator |
通过在绕组线圈中串联型号为0.25 Ω/1 W低温漂无感、 精度为1%的电阻,测试步进电机绕组电流波形. 步进电机高速运行时,采用一般的恒流细分控制方式,设定斩波频率为10 kHz,绕组电流波形如图 12所示. 由图可见,电流毛刺多、 纹波大,且在过零点不平滑,存在着一定的失真.
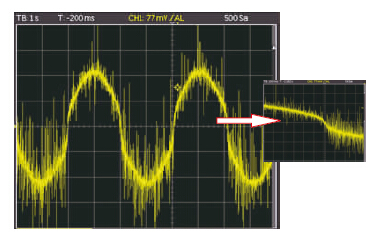 |
| 图 12 一般的恒流细分控制方式下绕组电流波形 Fig. 12 Waveform of winding current with the general constant current subdivision control mode |
在256细分下,加入电流快、 慢混合衰减模式后,其中fL取50 kHz,fH取200 kHz,fL和fH间上升段采用曲线1方式,同时提高斩波频率到20 kHz,绕组电流波形如图 13所示. 采用优化的控制策略后,绕组电流的毛刺大大减少且纹波小,几乎为完整的正弦波. 并且,应用在高精密微型实验仪中,对各项指标进行测试均满足要求.
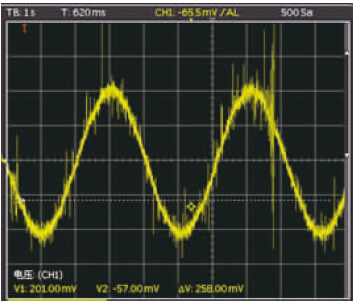 |
| 图 13 恒频20 kHz, 电流混合衰减模式下绕组电流波形 Fig. 13 Waveform of winding current with 20 kHz frequency and mixed current decay mode |
本文首先分析了目前一般的步进电机控制方法,对比了几种典型控制方式,提出了基于FPGA的步进电机电流优化控制策略. 然后分析了恒频斩波与电流快、 慢衰减相结合的控制方式,该方式一方面可以获得更高的步进精度,避免运行中的过冲与失步; 另一方面提高了步进电机高、 低速运行性能. 最后,在某型号高精密微型操作仪上
进行了实际测试,测试结果满足各项指标要求,且运行精度高、 噪声低. 因此,本文所述的方法不仅适用高精密控制场合,还可应用于多轴伺服系统的控制
| [1] | 张新荣, 徐保国. 基于正弦细分驱动技术的步进电机控制系统设计[J]. 电测与仪表, 2010, 47(8):69-72. Zhang X R, Xu B G. Design of stepper motor control system based on sine-subdivide drive[J]. Electrical Measurement & Instrumentation, 2010, 47(8):69-72. |
| [2] | 付朝阳, 刘景林, 常威威. 高精度二相混合式步进电机控制系统研究[J]. 计算机测量与控制, 2009, 17(7):1276-1278. Fu Z Y, Liu J L, Chang W W. Research of high precision control system of two-phase hybrid stepping motor[J]. Computer Measurement and Control, 2009, 17(7):1276-1278. |
| [3] | 杨秀增, 黄露. 二相混合式步进电机SPWM细分驱动器的FPGA设计[J]. 微电机, 2011, 44(2):102-104. Yang X Z, Huang L. Design of SPWM subdivided driving for two-phase hybrid step motor using FPGA[J]. Micromotors, 2011, 44(2):102-104. |
| [4] | 林鑫, 余世明, 朱建江. 混合式步进电机细分控制方法优化策略研究与仿真[J]. 机电工程, 2012, 29(2):196-199. Lin X, Yu S M, Zhu J J. Research and simulation for optimization of subdivision control used in hybrid stepper motor[J]. Journal of Mechanical & Electrical Engineering, 2012, 29(2):196-199. |
| [5] | 任勇, 张文超. 基于FPGA的两相步进电机细分驱动器设计[J]. 杭州电子科技大学学报, 2011, 31(2):21-24. Ren Y, Zhang W C. Design of two-phase micro-step driver based on FPGA[J]. Journal of Hangzhou Dianzi University, 2011, 31(2):21-24. |
| [6] | 吴云, 陆锷, 赵海洋, 等. 基于FPGA的步进电机细分驱动器的设计[J]. 自动化仪表, 2009, 30(10):61-63. Wu Y, Lu E, Zhao H Y, et al. Design of FPGA-based micro stepping motor driver[J]. Process Automation Instrument, 2009, 30(10):61-63. |
| [7] | Ma X J, Li C G, Cai Z, et al. The design of drive circuit with high-power output for two-phase hybrid stepping motor based on BY-5064[J]. Computer Aided Drafting, Design and Manufacturing, 2011, 21(1):28-32. |
| [8] | 宰文姣, 汪华章. 步进电机驱动控制系统的设计和实现[J]. 煤矿机械, 2013, 34(7):157-159. Zai W J, Wang H Z. Design and implementation of step motor drive and control system[J]. Coal Mine Machinery, 2013, 34(7):157-159. |
| [9] | Qi F Q, Jing X D, Zhao S Q. Design of stepping motor control system based on AT89C51 microcontroller[J]. Procedia Engineering, 2011, 15:2276-2280. |
| [10] | Le N Q, Jeon J W. An open-loop stepper motor driver based on FPGA[C]//Proceedings of the International Conference on Control, Automation and Systems. Piscataway, NJ, USA:IEEE, 2007:1322-1326. |
| [11] | Yang M D, Zhu M. A research of a new technique on hardware implementation of control algorithm of high-subdivision for stepper motor[C]//Proceedings of the 5th IEEE Conference on Industrial Electronics and Applications (ICIEA). Piscataway, NJ, USA:IEEE, 2010:115-120. |
| [12] | 顾瑞娟, 王宇, 张善从. 基于FPGA的步进电机驱动控制系统设计[J]. 计算机工程与设计, 2012, 33(1):111-115. Gu R J, Wang Y, Zhang S C. Design of stepping motor driving control system based on FPGA[J]. Computer Engineering and Design, 2012, 33(1):111-115. |
| [13] | Yuan W H, Cheng L, Xue M G, et al. Design of a step-motor control system based on FPGA[C]//Proceedings of the 8th International Conference on Electronic Measurement and Instruments. Piscataway, NJ, USA:IEEE, 2007:4874-4877. |
| [14] | 李婧, 金占雷. 两相步进电机单极性细分驱动器的实现[J]. 电机与控制应用, 2012, 39(3):14-18. Li J, Jin Z L. Design of two-phase stepping motor unipolar subdivision driver[J]. Electric Machine and Control Application, 2012, 39(3):14-18. |
| [15] | 徐志跃, 文招金, 陈伟海. 基于FPGA的两相步进电机细分驱动电路设计[J]. 电气传动, 2008, 38(4):59-62. Xu Z Y, Wen Z J, Chen W H. Design of two-phase micro stepping driver based on FPGA[J]. Electric Drive, 2008, 38(4):59-62. |
| [16] | 冒建亮, 叶桦, 张舒哲. 基于FPGA的变频控制系统的实现[J]. 东南大学学报:自然科学版, 2012, 42(S1):25-30. Mao J L, Ye H, Zhang S Z. Design of frequency control system based on FPGA[J]. Journal of Southeast University:Natural Science Edition, 2012, 42(S1):25-30. |
| [17] | 王邦继, 刘庆想, 周磊, 等. FPGA在多轴步进电机控制器中的应用[J]. 电机与控制学报, 2012, 16(3):78-82. Wang B J, Liu Q X, Zhou L, et al. FPGA-based multiple-axis stepper motor controller[J]. Electric Machines and Control, 2012, 16(3):78-82. |
| [18] | Juan Y, Kang H M, Wang Y S, et al. A control system of three-axis stepper motor based on the FPGA[C]//Proceedings of 2013 International Conference on Mechatronic Sciences, Electric Engineering and Computer (MEC). Piscataway, NJ, USA:IEEE, 2013:3334-3337. |
| [19] | Qi Q F, Jing X D, He K. Control system of stepper motor based on roundness and cylindricity measuring virtual instrument[J]. Procedia Engineering, 2011, 15:2281-2285. |
| [20] | 赵立辉, 霍春宝. 基于FPGA的步进电机多轴联动控制系统[J]. 电机与控制应用, 2013, 40(11):42-45, 58. Zhao L H, Huo C B. Control system for multi-axis stepper motor based on FPGA[J]. Electric Machines and Control Application, 2013, 40(11):42-45, 58. |



