2. 浙江工业大学信息工程学院, 浙江杭州 310014
2. College of Information Engineering, Zhejiang University of Technology, Hangzhou 310014, China
1 引言
近年来,针对正系统的动力学性质的研究,特别是其稳定性的研究引起了国内外学者的广泛关注[1, 2, 3]. 文[4]中,Farina和Rinaldi对无时滞线性正系统的稳定性进行了研究,给出了状态渐近稳定和对角二次稳定的等价关系. 文[5, 6]利用线性Copositive Lyapunov函数研究无时滞切换系统的稳定性,建立了系统指数稳定判据. 文[7, 8]利用Metzler矩阵和Hurwitz矩阵的性质研究含有执行器饱和的正系统稳定性,通过线性规划方法导出了保证闭环系统为正系统并且状态渐近稳定的状态反馈控制器. 由于实际系统中普遍存在时滞现象,而时滞往往导致系统不稳定. 因此,文[9, 10]建立了含有界时变时滞正系统渐近稳定的充要条件,通过与无时滞正系统稳定性条件的比较,得出了有界时滞不影响正系统渐近稳定性的结论. 文[11]利用线性Copositive Lyapunov泛函法以及平均驻留时间理论,给出了一类时变时滞切换正系统控制器的设计方法,使得闭环系统指数稳定且满足L1性能指标.文[12]采用平均驻留时间方法进一步研究了时变时滞正系统的镇定问题. 文[13, 14]则考虑了含有定常时滞的正系统输入受限情况下的镇定问题.
以上文献均是建立在系统模型精确获得且系统状态或输入不受限制的基础上. 但现实生活中,由于受到原件老化和灵敏度等因素的影响,实际系统往往存在建模不确定性,而模型的不确定性将严重影响系统的稳定性. 此外,控制元件的物理限制将导致执行器存在如饱和、 死区等非线性特征,从而导致系统性能下降或失稳. 因此在系统稳定性研究中,系统不确定性[15, 16, 17]和输入或状态受限[18]问题是不可忽视的. 但对于同时存在模型不确定性和控制、 状态受限的正系统,其鲁棒镇定问题还少有研究.
因此,本文着力研究一类含有时变时滞的参数不确定系统输入和状态受限下的鲁棒镇定问题. 利用正系统稳定性理论和线性规划方法,给出鲁棒状态反馈控制器设计算法. 该算法既能保证闭环系统为正系统又能确保系统状态渐近稳定,同时输入或状态受限. 仿真结果表明该算法是有效的.
2 预备知识本文中 表示集合{1,2,…,p},其中p为正整数;
表示集合{1,2,…,p},其中p为正整数;  表示集合{0,1,2,…,p};Rn+(Rn0,+)表示n维正(非负)向量集;Am×n=(aij)m×n,Bm×n=(bij)m×n,Cm×n=(cij)m×n,Am×n
表示集合{0,1,2,…,p};Rn+(Rn0,+)表示n维正(非负)向量集;Am×n=(aij)m×n,Bm×n=(bij)m×n,Cm×n=(cij)m×n,Am×n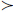 (
(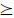 )Bm×n表示aij>(≥)bij(i∈m,j∈n), Am×n∈[Bm×n,Cm×n]表示aij∈[bij,cij](i∈
)Bm×n表示aij>(≥)bij(i∈m,j∈n), Am×n∈[Bm×n,Cm×n]表示aij∈[bij,cij](i∈
考虑连续系统:
.jpg)
其中,x(t)∈Rn是状态变量,Ai∈Rn×n(i∈ )是系统矩阵,时变时滞<
)是系统矩阵,时变时滞< i(t)≥0(i∈
i(t)≥0(i∈ )是连续有界函数,φ: [-
)是连续有界函数,φ: [- ,0]→R0,+(
,0]→R0,+(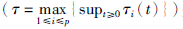 )是系统初始状态.
)是系统初始状态.
定义1[15]若对任意φ(t)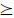 0(t∈[-
0(t∈[- ,0])有x(t)
,0])有x(t)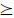 0(t≥0)成立,则称系统(1)为正系统.
0(t≥0)成立,则称系统(1)为正系统.
定义2 设An×n=(aij)n×n. 若aij≥0(i≠j),则称A为Metzler矩阵.
引理1[20] 若A为Metzler矩阵,则eAt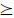 0(t≥0).
0(t≥0).
引理2[19]系统(1)为正系统当且仅当A0∈M,Ai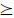 0(i∈
0(i∈ ).
).
引理3[14] 对系统(1),下述结论等价:
(i) 若0 φ(t)
φ(t) (t∈[-
(t∈[- ,0]),则0
,0]),则0 x(t)
x(t) <x(t≥0)
(ii) A0∈M,Ai
<x(t≥0)
(ii) A0∈M,Ai 0(i∈p),(
0(i∈p),(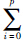 Ai)<x
Ai)<x 0
其中,<x∈Rn+.
0
其中,<x∈Rn+.
引理4[14] 若系统(1)为正系统,则系统(1)渐近稳定当且仅当存在向量λ∈Rn+,使得
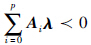
考虑一类不确定连续系统:
.jpg)
其中,A*i∈[Ai,Ai](i∈ )为区间不确定矩阵,Ai与Ai为已知常数矩阵. 连续有界时滞
)为区间不确定矩阵,Ai与Ai为已知常数矩阵. 连续有界时滞 i(t)(i∈
i(t)(i∈ t≥0)的所有下界inft≥0
t≥0)的所有下界inft≥0 i(t)(i∈
i(t)(i∈ 都满足inft≥0
都满足inft≥0 i(t)>0(i∈
i(t)>0(i∈ ).
).
引理5 对任意A*i∈[Ai,Ai](i∈ ),系统(2)为正系统当且仅当A0∈M且Ai
),系统(2)为正系统当且仅当A0∈M且Ai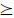 0(i∈
0(i∈ ).
).
必要性证明: 采用反证法. 若A0=(A(0)ij)n×n 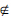 M,则至少存在一个元素A(0)ij <0(i≠j). 不失一般性,假设A(0)12<0. 取A*i=Ai(i∈
M,则至少存在一个元素A(0)ij <0(i≠j). 不失一般性,假设A(0)12<0. 取A*i=Ai(i∈ ),则系统(2)为
),则系统(2)为
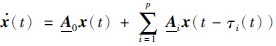
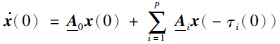
取x(0)=φ(0)=[0,k,0,…,0]T(k>0),x(t)≡φ(t)≡0,t∈[- ,0),考虑(0)的第1个分量
,0),考虑(0)的第1个分量 1(0). 显然
1(0). 显然 1(0)=A(0)12k<0,即x1(t)在零点某个右邻域(0,δ)内严格单调递减. 结合初始条件的设定x1(0)=0,有x1(t)<0(δ>t>0),与正系统定义矛盾,从而A0∈M. 类似地可以证明Ai
1(0)=A(0)12k<0,即x1(t)在零点某个右邻域(0,δ)内严格单调递减. 结合初始条件的设定x1(0)=0,有x1(t)<0(δ>t>0),与正系统定义矛盾,从而A0∈M. 类似地可以证明Ai 0(i∈
0(i∈ ).
).
充分性证明: 若A0∈M,由于A0 A*0,故A*0∈M. 若AiA0(i∈
A*0,故A*0∈M. 若AiA0(i∈ ),则A*i
),则A*i Ai
Ai 0. 结合引理2可知,对任意A*i∈[Ai,Ai](i∈
0. 结合引理2可知,对任意A*i∈[Ai,Ai](i∈ ),系统(2)是正系统. 引理5证毕.
),系统(2)是正系统. 引理5证毕.
引理6 若对任意A*i∈[Ai,Ai](i∈ ),系统(2)是正系统,则下述结论等价:
),系统(2)是正系统,则下述结论等价:
(i) 系统(2)渐近稳定.
(ii) 存在向量λ∈Rn+,满足:
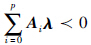
证明
(ii)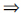 (i):若存在向量λ∈Rn+,满足
(i):若存在向量λ∈Rn+,满足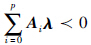 ,则根据
,则根据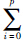 Ai
Ai
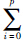 A*i,有0
A*i,有0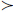
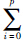 Aiλ
Aiλ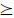
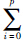 A*iλ. 结合引理4可知: 对任意A*i∈[Ai,Ai](i∈
A*iλ. 结合引理4可知: 对任意A*i∈[Ai,Ai](i∈ ),系统(2)渐近稳定.
),系统(2)渐近稳定.
(i)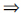 (ii):若对任意A*i∈[Ai,Ai](i∈
(ii):若对任意A*i∈[Ai,Ai](i∈ ),正系统(2)渐近稳定. 不妨设A*i=Ai,根据引理4可知:
),正系统(2)渐近稳定. 不妨设A*i=Ai,根据引理4可知: 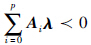 引理6证毕.
引理6证毕.
定理1 对系统(2),下述结论等价:
(i) 对任意A*i∈[Ai,Ai](i∈ ),若0
),若0 φ(t)
φ(t) <x(t∈[-
<x(t∈[- ,0]),则:
,0]),则:
0 x(t)
x(t) <x,t≥0
<x,t≥0
(ii)A0∈M,Ai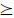 0(i∈
0(i∈ ),(
),(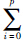 Ai)<x
Ai)<x 0(3)
0(3)
其中,<x∈Rn+.
证明
(i) (ii):取A*i=Ai(i=
(ii):取A*i=Ai(i= ),φ(t)=<x(t∈[-
),φ(t)=<x(t∈[- ,0]),则
,0]),则
.jpg)
又
.jpg)
综合式(4)、 式(5)可知x(0)的右导数 +(0)
+(0) 0,
即
0,
即
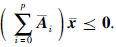
结合条件(i)与正系统定义,易知对任意A*i∈[Ai,Ai],系统(2)是正系统. 根据引理5有A0∈M,Ai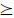 0(i∈
0(i∈ ).
).
(ii)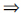 (i): 若A0∈M,Ai
(i): 若A0∈M,Ai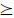 0(i∈
0(i∈ ),根据引理5易知对任意A*i∈[Ai,Ai],系统(2)为正系统. 另一方面,对于任意A*i∈[Ai,Ai](i∈
),根据引理5易知对任意A*i∈[Ai,Ai],系统(2)为正系统. 另一方面,对于任意A*i∈[Ai,Ai](i∈ ),系统(2)的状态向量为
x(t)=eA*0tφ(0)+∫t0eA*0s
),系统(2)的状态向量为
x(t)=eA*0tφ(0)+∫t0eA*0s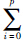 A*ix(t-s-
A*ix(t-s- i(t-s))ds
i(t-s))ds
其中,A*0为Metzler矩阵. 当eA*0s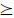 0(t≥0),有:
0(t≥0),有:
.jpg)
.jpg)
.jpg)
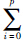 Ai
Ai 0易知
0易知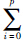 A*i
A*i 0,进而:
0,进而:
.jpg)
综合式(8)、 式(9),可知:
.jpg)
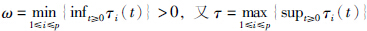
得到
- ≤t-s-
≤t-s- i(t-s)≤0
i(t-s)≤0
由(i)可知x(t-s- i(t-s))
i(t-s)) <x,则:
∫t0eA*0s
<x,则:
∫t0eA*0s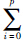 A*i(x(t-s-
A*i(x(t-s- i(t-s))-<x)ds
i(t-s))-<x)ds 0
结合式(10)易知x(t)
0
结合式(10)易知x(t) <x(t∈[0,ω]).
<x(t∈[0,ω]).
下面利用数学归纳法,证明上述结论对t≥0恒成立.
假设当t∈[(n-1)ω,nω]时结论成立,则当t∈[nω,(n+1)ω]时,有:
.jpg)
- ≤t-s-
≤t-s- i(t-s)≤0
i(t-s)≤0
故根据(i)有x(t-s- i(t-s))-<x
i(t-s))-<x 0,进而:
∫tnωeA*0s
0,进而:
∫tnωeA*0s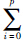 A*i(x(t-s-
A*i(x(t-s- i(t-s))-<x)ds
i(t-s))-<x)ds 0
0
再结合归纳假设:
∫nω0eA*0s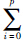 A*i(x(t-s-
A*i(x(t-s- i(t-s))-<x)ds
i(t-s))-<x)ds 0
和式(11)可知x(t)
0
和式(11)可知x(t) <x(t≥0). 定理1证毕
<x(t≥0). 定理1证毕
(i) 对任意A*i∈[Ai,Ai](i∈ ),系统(2)为正系统且状态渐近稳定.
),系统(2)为正系统且状态渐近稳定.
证明 由引理5和引理6易知(i)与(ii)等价,证明略.
注1 引理5给出了确保不确定系统(2)为正系统的充要条件. 在不确定系统(2)为正系统的前提下,引理6建立了保证系统状态渐近稳定的充要条件.定理2在此基础上,进一步建立了保证不确定系统(2)为正系统且渐近稳定的充要条件.
注2 由文[10]得知: 连续有界时滞不影响连续正系统的渐近稳定. 故对系统(2),若时变时滞 i(t)仅满足
i(t)仅满足 i(t)≥0(i∈
i(t)≥0(i∈ ),定理1、 定理2仍然成立.
),定理1、 定理2仍然成立.
注3 定理1建立了保证不确定系统(2)的状态非负并且有界的充要条件. 定理2建立了不确定系统(2)的状态非负并且渐近稳定的充要条件. 不难看出条件式(12)比条件式(3)要求更为严格. 若式(12)满足,则系统(2)为正系统且状态渐近稳定. 而式(3)只保证系统为正系统并且状态有界.
4 鲁棒状态反馈控制器设计考虑系统:
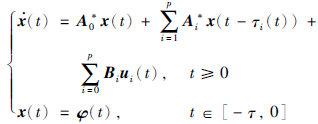
 ),
), i(t),
i(t), 在系统(2)给出定义. 设计如下状态反馈控制器:
在系统(2)给出定义. 设计如下状态反馈控制器:

 ),闭环系统为
),闭环系统为
.jpg)
 ui(t)
ui(t) xi(i∈
xi(i∈ ,t≥0),其中为任意给定向量.
,t≥0),其中为任意给定向量.
首先给出保证闭环系统(13)为正系统并且状态有界、 输入受限的充要条件.
定理3 任意给定向量0 xi∈Rm+(i∈
xi∈Rm+(i∈ ),对闭环系统(13),下述结论等价:
(i) 当0
),对闭环系统(13),下述结论等价:
(i) 当0 φ(t)
φ(t) <x(t∈[-
<x(t∈[- ,0])时:
0
,0])时:
0 x(t)
x(t) <x(t≥0),0
<x(t≥0),0 ui(t)
ui(t) xi,i∈
xi,i∈ ,t≥0
同时成立,其中<x∈Rn+.
,t≥0
同时成立,其中<x∈Rn+.
(ii) 存在列向量k(i)j∈Rm0,+(i∈ ,j∈n),<x∈Rn+,使得
,j∈n),<x∈Rn+,使得
.jpg)
成立,其中Al=(A(l)ij)n×n(l∈ ,i∈n,j∈n),b(l)i(l∈
,i∈n,j∈n),b(l)i(l∈ ,i∈n)表示矩阵Bl的第i个行向量,相应的控制增益:
,i∈n)表示矩阵Bl的第i个行向量,相应的控制增益:
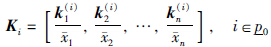
证明
(ii)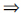 (i): 易见A(0)ij<xj+b(0)ik(0)j≥0(i,j∈n,i≠j)等价于:
(i): 易见A(0)ij<xj+b(0)ik(0)j≥0(i,j∈n,i≠j)等价于:
.jpg)
 )等价于:
)等价于:.jpg) 由此:
由此:
.jpg)
结合定理1可知: 当0 φ(t)
φ(t) <x时,有0
<x时,有0 x(t)
x(t) <x(t≥0). 所以:
<x(t≥0). 所以:
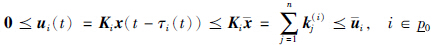
其中 0(t)=0.
0(t)=0.
(i)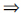 (ii): 不妨设φ(t)≡(t∈[-
(ii): 不妨设φ(t)≡(t∈[- ,0]),则:
,0]),则:
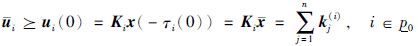
根据条件(i)和定理1易知:
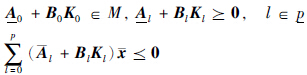
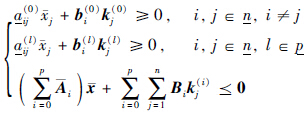
下面采用反证法证明k(l)j∈Rm0,+(l∈ ,j∈n). 不失一般性,设列向量k(1)2的第3个分量k(1)23<0,φ(t)=[0,m,0,…,0]T(m>0,t∈[-
,j∈n). 不失一般性,设列向量k(1)2的第3个分量k(1)23<0,φ(t)=[0,m,0,…,0]T(m>0,t∈[- ,0]),则u1的第3个分量u13在零点的取值u13(0)=k(1)23m<0,这与已知条件矛盾. 定理3证毕.
,0]),则u1的第3个分量u13在零点的取值u13(0)=k(1)23m<0,这与已知条件矛盾. 定理3证毕.
下面的定理给出了保证闭环系统(13)为正系统并且渐近稳定、 状态和输入受限的充要条件.
定理4 任意给定向量0xi∈Rm+(i∈ ),下述结论等价:
),下述结论等价:
(i) 闭环系统(13)为正系统且渐近稳定. 当0 φ(t)
φ(t) <x(t∈[-
<x(t∈[- ,0])时,有:
,0])时,有:
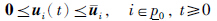
(ii)存在列向量k(i)j∈Rm0, +(i∈ , j∈n), <x∈Rn+, 使得
, j∈n), <x∈Rn+, 使得
.jpg)
成立,相应的控制增益:
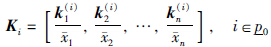
证明
(ii)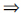 (i): 易见若式(18)成立,则式(14)成立. 根据定理3,当0
(i): 易见若式(18)成立,则式(14)成立. 根据定理3,当0 φ(t)
φ(t) <x(t∈[-
<x(t∈[- ,0])时,有:
,0])时,有:
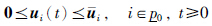
综合式(15)~式(17), 并结合定理2可知: 闭环系统(13)为正系统且渐近稳定当且仅当:
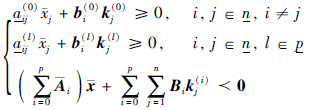
成立.
(i)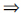 (ii):与定理3证明方法类似. 证毕.
(ii):与定理3证明方法类似. 证毕.
注4 定理2给出保证不确定系统(2)渐近稳定的等价条件. 定理3在稳定性分析的基础上,给出求解状态上界<x的算法. 使得在初始状态不大于该上界的情况下,闭环系统(13)为正系统并且状态有界、 输入受限. 进一步,定理4的算法还保证了闭环系统(13)状态渐近稳定.
注5 一方面,定理1和定理2对于开环系统为非正系统同样适用. 另一方面,对任意连续有界时滞 i(t)≥0(i∈
i(t)≥0(i∈ ),定理3和定理4亦成立.
),定理3和定理4亦成立.
最后,对闭环系统(13)研究相应的状态受限问题.
定理5 对闭环系统(13)以及任意给定的向量xmax∈Rn+,下述结论等价:
(i) 闭环系统(13)为正系统且渐近稳定. 当0 φ(t)
φ(t) <x(t∈[-
<x(t∈[- ,0],<x∈Rn+)时,有:
,0],<x∈Rn+)时,有:
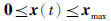
(ii)存在列向量k(i)j∈Rm0,+(i∈ ,j∈n),<x∈Rn+,使得
,j∈n),<x∈Rn+,使得
.jpg)
相应的控制增益
证明 类似定理4,省略.
5 数值例子首先考虑稳定性分析问题.
例1 对系统(2),选取系统矩阵如下:
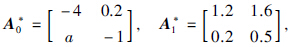
 (t)=|sint|.
(t)=|sint|.
当0≤a≤0.577时,式(12)有可行解:
a=0,λ=[92.468 895.385 8]T
a=0.577,λ=[84.578 5131.563 5]T
当a≥0.578时,式(12)无解. 根据定理2,当0≤a≤0.577,系统(2)为正系统且渐近稳定; 当a≥0.578时,系统(2)为正系统,但状态不渐近稳定. 图 1~图 4给出了取不同数值时相应的状态轨迹.
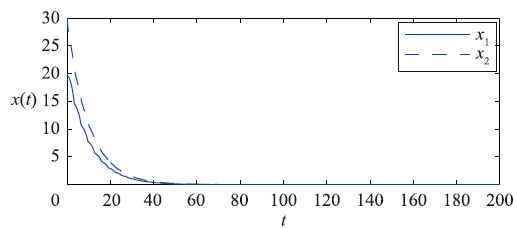 |
| 图 1 状态变量x1(t)、 x2(t)的时间响应曲线,a=0.3 Fig. 1 Time response curves of the state variables x1(t) and x2(t)when a=0.3 |
 |
| 图 2 状态变量x1(t)、x2(t)的时间响应曲线,a=0.577Fig. 2 Time response curves of the state variables x1(t) and x2(t) when a=0.577 |
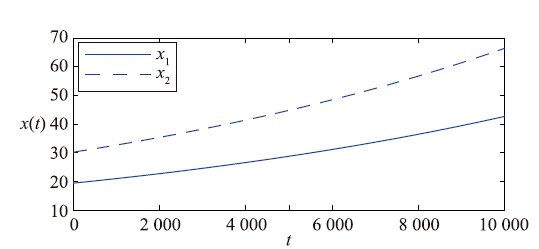 |
| 图 3 状态变量x1(t)、 x2(t)的时间响应曲线,a=0.578Fig. 3 ime response curves of the state variables x1(t) and x2(t) when a=0.578 |
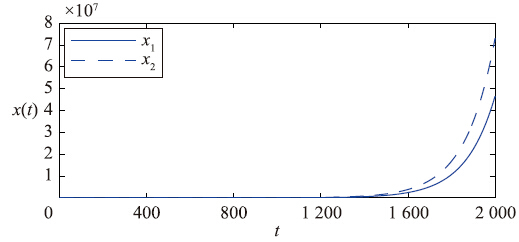 |
| 图 4 状态变量x1(t)、 x2(t)的时间响应曲线,a=0.6 Fig. 4 ime response curves of the state variables x1(t) and x2(t) when a=0.6 |
下面将利用数值算例研究反馈控制器的设计问题.
例2 对闭环系统(13),假设系统矩阵如下:

不失一般性,选取:
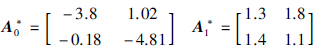
 (t)=|sin t|,控制器范围由:
(t)=|sin t|,控制器范围由:
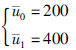
确定. 利用线性规划求解式(18),可得
x=[15.162 99.027 7)]T
K0=[10.896 31.208 1]
K1=[0.337 00.251 5]
注意到A*0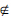 M,即开环系统不是正系统. 因此当初始状态非负,其状态轨迹可能超出正象限. 选取初始状态φ(t)=[15, 9]T,如图 5所示,闭环系统(13)的状态轨迹始终在非负象限内,渐近稳定,同时满足x(t)
M,即开环系统不是正系统. 因此当初始状态非负,其状态轨迹可能超出正象限. 选取初始状态φ(t)=[15, 9]T,如图 5所示,闭环系统(13)的状态轨迹始终在非负象限内,渐近稳定,同时满足x(t) <x. 相应的,控制输入满足受限条件,如图 6所示. 显然在开环系统为非正系统的情况下,控制器仍能保证闭环系统为正系统并且状态渐近稳定,输入受限. 需要指出的是,利用定理4得到的状态上界<x=[15.162 99.027 7]T仅为系统的一个可行解,不一定唯一. 所以若存在某个t1∈[-
<x. 相应的,控制输入满足受限条件,如图 6所示. 显然在开环系统为非正系统的情况下,控制器仍能保证闭环系统为正系统并且状态渐近稳定,输入受限. 需要指出的是,利用定理4得到的状态上界<x=[15.162 99.027 7]T仅为系统的一个可行解,不一定唯一. 所以若存在某个t1∈[- ,0],使得φ(t1),闭环系统(13)仍然有可能为正系统且渐近稳定,同时满足输入受限.
,0],使得φ(t1),闭环系统(13)仍然有可能为正系统且渐近稳定,同时满足输入受限.
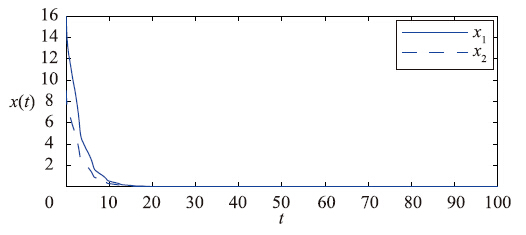 |
| 图 5 状态变量x1(t)、 x2(t)的时间响应曲线 Fig. 5 Time response curves of the state variables x1(t) and x2(t) |
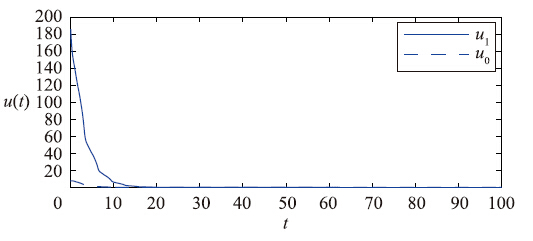 |
| 图 6 控制输入u0(t)、 u1(t)的时间响应曲线Fig. 6 Time response curves of the control input u0(t) and u1(t) |
例3 对闭环系统(13),选取系统矩阵如例2所示. 状态变量上界由xmax=[20, 40]T给定. 根据定理5,利用线性规划求解式(19)可得:
<x=[19.520 9, 11.688 9]T
K0=[11.338 6, 2.191 3]
K1=[0.359 9, 0.358 9]
不失一般性,初始状态取为φ(t)=[19, 11]T(t∈[- ,0]). 从图 7不难看出,闭环系统(13)的状态始终非负,同时满足0
,0]). 从图 7不难看出,闭环系统(13)的状态始终非负,同时满足0 <x
<x xmax.
xmax.
 |
| 图 7 状态变量x1(t)、 x2(t)的时间响应曲线Fig. 7 Time response curves of the state variables x1(t) and x2(t) |
针对一类输入受限的不确定系统,采用线性规划方法,给出保证闭环系统为正系统并且状态渐近稳定的控制器设计方法. 进一步,将该方法推广应用到状态和输入受限的问题. 仿真结果表明控制算法是有效性的. 进一步的工作是对不确定正系统进行性能分析.
| [1] | Ngoc P H A. Stability of positive differential systems with delay[J]. IEEE Transactions on Automatic Control, 2013, 58(1):203-209. |
| [2] | Feyzmahdavian H R, Charalambous T, Johansson M. Exponential stability of homogeneous positive systems of degree one with time-varying delays[J]. IEEE Transactions on Automatic Control, 2014, 59(6):1594-1599. |
| [3] | Zhang J F, Han Z Z, Wu H. Robust finite-time stability and stabilization of switched positive systems[J]. IET Control Theory and Applications, 2014, 8(1):67-75. |
| [4] | Farina L, Rinaldi S. Positive linear systems:Theory and applications[M]. New York, USA:John Wiley & Sons Inc, 2000. |
| [5] | Mason O, Shorten R. On linear copositive Lyapunov functions and stability of switched positive linear systems[J]. IEEE Transactions on Automatic Control, 2007, 52(7):1346-1349. |
| [6] | Liu X W. Stability analysis of switched positive systems:A switched linear Lyapunov function method[J]. IEEE Transaction on Circuits and Systems II:Express Briefs, 2009, 56(5):414-418. |
| [7] | Rami M A, Tadeo F. Controller synthesis for positive linear systems with bounded controls[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2007, 54(2):151-155. |
| [8] | Rami M A, Tadeo F, Benzaouia A. Control of constrained positive discrete systems[C]//Proceedings of the 2007 American Control Conference. Piscataway, NJ, USA:IEEE, 2007:5851-5856. |
| [9] | Liu X W. Stability and stabilization of positive systems with delays[C]//Proceedings of the 2009 International Conference on Communications, Circuits and Systems. Piscataway, NJ, USA:IEEE, 2009:908-912. |
| [10] | Liu X W, Yu W, Wang L. Stability analysis for continuous-time positive systems with time-varying delays[J]. IEEE Transactions on Automatic Control, 2010, 55(4):1024-1028. |
| [11] | Xiang M, Xiang Z R. Stability, L1-gain and control synthesis for positive switched systems with time-varying delay[J]. Nonlinear Analysis:Hybrid Systems, 2013, (9):9-17. |
| [12] | Xiang M, Xiang Z R, Karimi H R. Stabilization of positive switched systems with time-varying delays under asynchronous switching[J]. International Journal of Control, Automation and Systems, 2014, 12(5):939-947. |
| [13] | Liu X W, Wang L, Yu W S, et al. Constrained control of positive discrete-time systems with delays[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2008, 55(2):193-197. |
| [14] | Liu X W. Constrained control of positive systems with delays[J]. IEEE Transactions on Automatic Control, 2009, 54(7):1596-1600. |
| [15] | 曹科才, 刘春香, 高翔, 等. 不确定时变时滞多个体系统的鲁棒H∞一致性控制[J]. 信息与控制, 2012, 41(5):608-616. Cao K C, Liu C X, Gao X, et al. Robust H∞ consensus control for uncertain multi-agent system with time-varying delays[J]. Information and Control, 2012, 41(5):608-616. |
| [16] | 逄海萍, 唐功友, 孙慧影. 一类时滞不确定系统的最优滑模设计[J]. 信息与控制, 2009, 38(1):87-92, 97. Pang H P, Tang G Y, Sun H Y. Optimal sliding mode design for a class of uncertain systems with time-delay[J]. Information and Control, 2009, 38(1):87-92, 97. |
| [17] | 邓涛, 姚宏, 杜军, 等. 一类不确定高阶随机非线性系统的自适应动态面控制[J]. 信息与控制, 2014, 43(4):457-462. Deng T, Yao H, Du J, et al. Adaptive dynamic surface control for a class of uncertain high-order stochastic nonlinear systems[J]. Information and Control, 2014, 43(4):457-462. |
| [18] | 康忠健, 王清伟, 黄磊, 等. 基于改进遗传算法的自抗扰控制器参数优化[J]. 信息与控制, 2008, 37(5):588-592. Kang Z J, Wang Q W, Huang L, et al. Parameter optimization of active-disturbance-rejection controller based on improved genetic algorithm[J]. |
| [19] | Rami M A, Helmke U, Tadeo F. Positive observation problem for linear time-delays positive systems[C]//Proceedings of the 15th Mediterranean Conference on Control and Automation. Piscataway, NJ, USA: IEEE, 2007: 1-6. |
| [20] | Kaczorek T. Positive 1D and 2D systems[M]. London, UK: Springer-Verlag, 2002. |



