2. 集美大学信息工程学院, 福建厦门 361021;
3. 华侨大学信息科学与工程学院, 福建厦门 361021
2. College of Information Engineering, Jimei University, Xiamen 361021, China;
3. College of Information Science and Engineering, Huaqiao University, Xiamen 361021, China
1 引言
信号在采集和转换过程中,由于受测量对象、 测量环境、 测量方法等因素的影响,不可避免地会遭受到各种噪声的影响,甚至被噪声完全淹没. 因此,对信号进行降噪处理是十分必要的[1, 2]. 语音降噪技术是语音信号处理的一个重要分支,它在解决噪声污染、 提高语音质量等方面发挥重要的作用.
目前,语音降噪方法已比较成熟. 常用的语音降噪技术主要采用滤波的方法,如递归最小二乘(recursive least square,RLS)法、 线性滤波法、 扩展型卡尔曼滤波法、 粒子滤波法、 小波滤波法、 自适应滤波法等[3, 4, 5, 6]. 由于语音信号频谱分布宽、 具有时变非线性,且包含的噪声分布特性复杂多样,因此通常采用自适应滤波的方法对其降噪. 但自适应滤波的算法复杂,实时性较差[7, 8, 9, 10].
量子随机滤波(quantum stochastic filter,QSF)运用量子力学的基本原理,从微观角度构建信号的势函数,根据薛定谔方程计算信号的概率密度分布函数(PDF)的时间、 空间演化,从而估计信号的真值,实现信号的滤波. 量子随机滤波是一种新型的、 非线性、 非高斯、 非平稳、 高精度的滤波算法.
1992年,Dawes把量子力学与神经网络理论相结合,提出了量子神经动力学(Quantum NeuroDynamics,QND)的概念,阐述了应用量子力学进行滤波的基本原理,并给出了量子随机滤波器的基本结构,但是论文没有给出量子随机滤波的具体算法[11]. 2004年~2006年,Behera和Kar提出了递归量子神经网络(recurrent quantum neural network,RQNN)和量子随机滤波的概念,改进了Dawes所提出的量子随机滤波器的结构,提出了基于神经网络的势函数梯度学习算法[12, 13, 14]. 文[12]对比了量子随机滤波与卡尔曼滤波的差异卡尔曼滤波的差异. 2007年,东南大学的朱仁祥和吴乐南把该算法应用于通信信号处理[15]. 2011年~2013年,Gandhi等把量子随机滤波应用于脑信号处理和人眼视觉跟踪等领域,取得了较好的效果[16, 17, 18].
本文首先介绍量子随机滤波的基本原理; 然后提出量子随机滤波的自适应学习算法,并利用该算法对含有噪声的语音信号进行滤波降噪; 最后对降噪效果进行了评价.
2 量子随机滤波的基本原理与实现算法 2.1 量子随机滤波的基本原理假设测量到的语音信号为数据序列y=[x1,x2,…xk]T,其中既含有真实信号又含有噪声信号. 因此,测量信号xk可以看成是真值信号zk和噪声信号νk的叠加,k为时间t的离散化表示,即:

根据中心极限定理,在统计上xk以zk为中心随机变化,随机变化的νk满足一定的分布规律. 如果把式(1)微观物化,则式(1)可以理解为: 一个微观粒子在特定的势场约束下运动,粒子的坐标位置为xk,由于微观粒子具有波动性,xk存在一定的随机偏差vk,xk的统计概率中心在zk.
假设粒子的质量为m,位置为x,约束粒子波动的势函数为V(x,t),粒子在位置x方向的概率密度为ρ(x,t),相应的波函数为ψ(x,t). 则粒子的运动满足薛定谔方程,如式(2)所示:
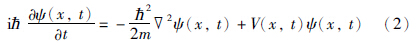
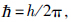 h为普朗克常量; x表示的位置可以是1维的,也可以是2维或3维的,本文中x为1维.
h为普朗克常量; x表示的位置可以是1维的,也可以是2维或3维的,本文中x为1维.
薛定谔方程是量子力学的基本方程,概率密度ρ(x,t)和波函数为ψ(x,t)之间满足:
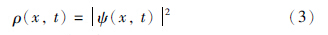
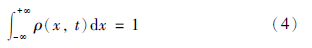
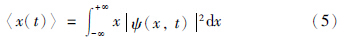
至此,对测量信号xk真值zk的估计转换为对k时刻粒子位置的估计,即计算k时刻粒子位置的数学期望.
2.2 量子随机滤波的实现算法量子随机滤波的实现过程如图 1所示.
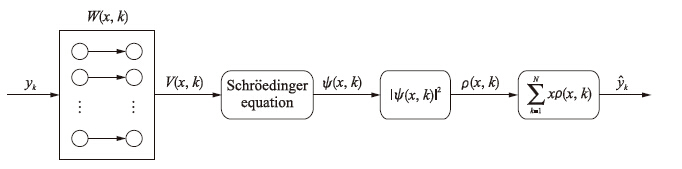 |
| 图 1 量子随机滤波过程框图Fig. 1 Quantum stochastic filter process diagram |
图 1中,yk为输入带噪声的测量信号;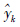 为输出滤波结果,即估计真值信号; W(x,k)为权值; V(x,k)为势函数.
为输出滤波结果,即估计真值信号; W(x,k)为权值; V(x,k)为势函数.
从图 1可知,量子随机滤波算法过程主要包括4个步骤[12, 18]:
(1) 构造势函数V(x,k);
(2) 根据势函数V(x,k),通过解薛定谔方程,计算波函数ψ(x,k);
(3) 根据波函数ψ(x,k),计算概率密度函数ρ(x,k);
(4) 根据概率密度函数ρ(x,k),计算估计值k. 其中第1个步骤最为关键. 构造势函数V(x,k)时必须利用薛定谔方程式(2)的孤立子解.因此,势函数V(x,k)可以构造成式(6)的形式:
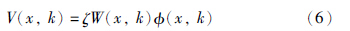
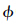 (x,k)为高斯基函数:
(x,k)为高斯基函数:
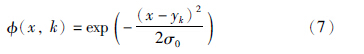
权值W(x,k)的更新采用自适应学习算法[18]:
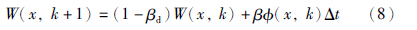
量子随机滤波算法中必须解薛定谔方程,薛定谔方程有多种解法,本文采用差分迭代法,即采用差商替代微商.
时间导数采用前向差分替代,即式(9):
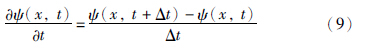
空间导数采用中心差分替代,即式(10):
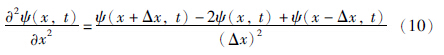
将式(9)和式(10)代入式(2),得:
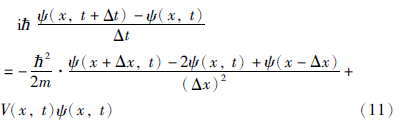
令xj=jΔx,tn=nΔt,ψ(xj,tn+Δt)写为ψn+1j,ψ(xj,tn)写为ψnj,ψ(xj-Δx,tn)写为ψnj-1,V(x,t)写为Vj,则式(11)可以改写为式(12):
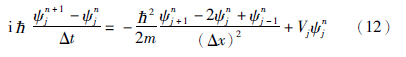
把式(12)改写为递归形式,如式(13)所示:
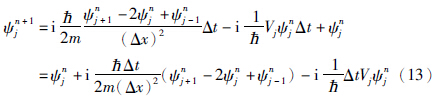
波函数ψ为复数,令ψ=realφ+iimagφ,代入式(13),可得实部、 虚部分离的递归格式,如式(14)所示:
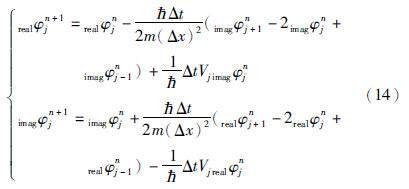
利用式(14),即可解薛定谔方程. 通过微扰法可证明式(13)收敛到式(9)的条件如式(15)所示[20]:
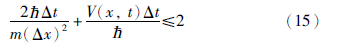
本文的实验过程: 用录音笔录制中央电视台新闻联播主持人郎永淳的一段播音,存储为“播音.wav”,采用频率为44 100 Hz,分辨率为16 bit. 由于语音数据太大,本实验只提取45 000个采样数据,内容为“今天的新闻联播”7个字的语音,存储为“新闻联播.wav”. 以“新闻联播.wav”中声道1的数据作为真值ytrue,然后向ytrue中分别加入不同程度、 不同类型的噪声以生成待测试信号ynoise. 采用本文提出的量子随机滤波算法对ynoise进行滤波降噪,输出滤波降噪后的估计结果yest. 最后对照真值ytrue对滤波降噪估计结果yest进行滤波降噪效果评价.
仿真中,量子随机滤波器的参数选择根据文[12]采用遗传算法(GA). 滤波器的参数为: 普朗克常数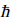 =1,质量m=1,神经元数N=60,时间步长Δt=0.001,空间步长Δx=0.1,学习系数β=0.5,学习遗忘因子βd=0.5,势函数系数ζ=0.1.
=1,质量m=1,神经元数N=60,时间步长Δt=0.001,空间步长Δx=0.1,学习系数β=0.5,学习遗忘因子βd=0.5,势函数系数ζ=0.1.
包含高斯白噪声的语音信号滤波降噪结果. 向ytrue中分别加入不同程度的高斯白噪声信号以生成待测试信号ynoise,ynoise的信噪比SNR(signal to noise ratio)水平分别控制在16 dB、 10 dB、 6 dB、 3 dB和0 dB.
当语音信号中包含6 dB的高斯白噪声时,滤波降噪效果如图 2所示.
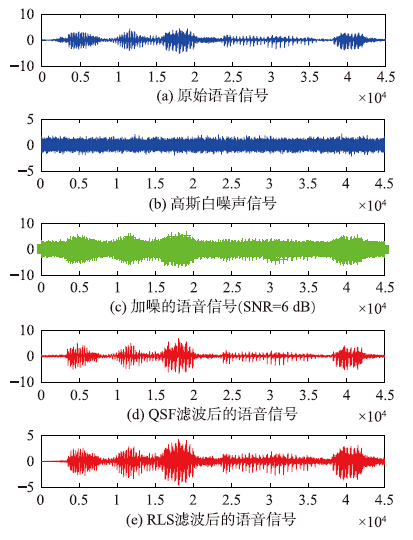 |
| 图 2 语音信号降噪前后波形(高斯白噪声,SNR=6 dB) Fig. 2 The speech waveforms after de-noising vs. before(Gauss white noise,SNR=6 dB) |
提取图 2中第13 000~16 000个语音数据,局部放大的波形如图 3所示.
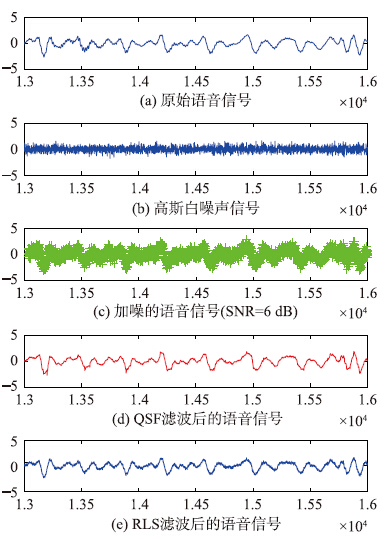 |
| 图 3 语音信号降噪前后波形局部放大图(高斯白噪声,SNR=6 dB)Fig. 3 The speech waveforms partial enlarged after de-noising vs. before (Gauss white noise,SNR=6 dB) |
从图 2和图 3可知:量子随机滤波降噪算法对语音信号中的高斯白噪声的降噪效果很明显,滤波降噪算法的好坏还可以采用信噪比SNR和均方根值误差RMSE(root mean square error)来衡量.
SNR的定义如式(16)所示:
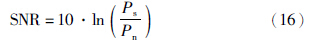
RMSE的定义如式(17)所示:

在真值信号中分别加入20 dB、 10 dB、 6 dB、 3 dB、 0 dB高斯白噪声信号,然后进行量子随机滤波,分别计算滤波后的SNR和RMSE,计算结果如表 1所示.
| 滤波前 | 滤波后 | ||
| SNR/dB | RMSE | SNR/dB | RMSE |
| 16 | 0.160 0 | 18.121 4 | 0.124 0 |
| 10 | 0.316 7 | 17.264 2 | 0.136 8 |
| 6 | 0.498 2 | 16.274 1 | 0.153 5 |
| 3 | 0.689 0 | 13.146 3 | 0.236 3 |
| 0 | 1.020 9 | 6.944 0 | 0.606 0 |
从表 1可知: 含噪声的语音信号经过量子随机滤波后大大提高了信噪比SNR,降低了均方根误差RMSE,滤波降噪效果明显.
(2) 包含周期性高斯白噪声的语音信号滤波降噪结果. 向ytrue中分别加入周期性变换的高斯白噪声信号生成待测试信号ynoise,ynoise的SNR为10 dB时的仿真波形如图 4所示.
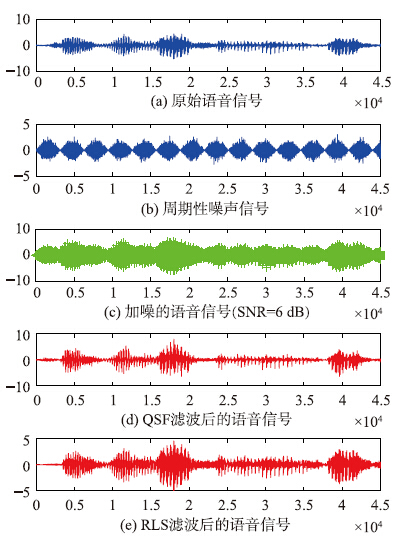 |
| 图 4 语音信号降噪前后波形(周期性噪声,SNR=6 dB)Fig. 4 The speech waveforms after de-noising vs. before (periodic noise,SNR=6 dB) |
局部放大图 4中的第13 000~16 000个语音数据,波形如图 5所示.
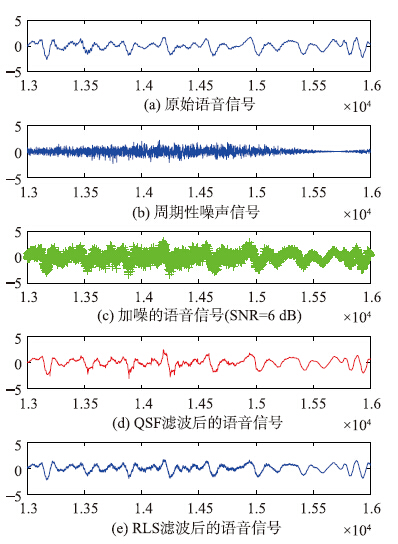 |
| 图 5 语音信号降噪前后波形局部放大图 (周期性白噪声,SNR=6 dB)Fig. 5 The speech waveforms partial enlarged after de-noising vs. before (periodic noise,SNR=6 dB) |
从图 4和图 5可知: 量子随机滤波器能有效地滤除语音信号中的周期性噪声,且效果明显.
(3) 包含脉冲噪声的语音信号滤波降噪结果. 向ytrue中分别加入脉冲噪声信号生成待测试信号ynoise,ynoise的SNR为10 dB时的仿真波形如图 6所示.
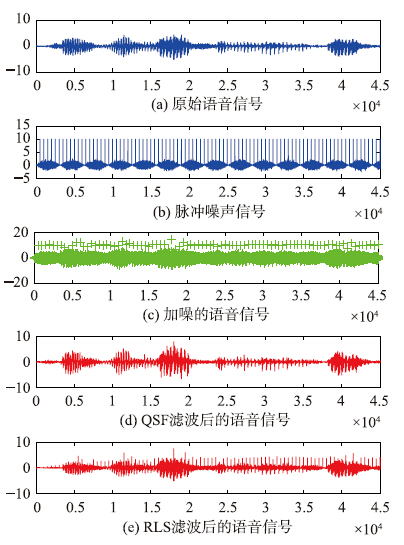 |
| 图 6 语音信号降噪前后波形(脉冲噪声)Fig. 6 The speech waveforms after de-noising vs. before (impluse noise) |
从图 6和图 7可以看出: 量子随机滤波器能有效地滤除语音信号中的脉冲噪声.
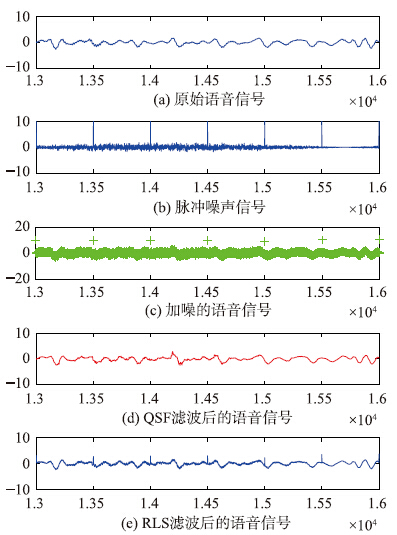 |
| 图 7 语音信号降噪前后波形局部放大图(脉冲噪声)Fig. 7 The speech waveforms partial enlarged after de-noising vs. before (impluse noise) |
对比图 2~图 7每幅图的最后两幅子图,可知:
(1) 量子随机滤波算法相对于传统RLS自适应滤波算法,不论是对应于普通高斯平稳噪声表现出的准确性,还是对于非平稳噪声时所表现出的自适应性,都要优于RLS滤波算法;
(2) 对于脉冲噪声,RLS并不能完全过滤掉脉冲分量,如图 6和图 7所示,而量子滤波算法几乎能全部滤除脉冲分量.
局部放大图 6中的第13 000~16 000个语音数据,波形如图 7所示.
4 结论本文提出一种语音信号降噪的新方法——量子随机滤波的自适应算法. 根据仿真效果来看,该算法能有效地对 包含有高斯白噪声、 周期性噪声、 脉冲噪声等不同类型的噪声的语音信号进行滤波降噪且效果明显. 由于量子随机滤波精度高、 适应性强,因此提供了一种与传统的滤波降噪算法(如RLS)完全不同的思路与方法. 但该方法也存在着一定的不足,即算法复杂,计算量较大.
| [1] | 沈赟, 张丽清. 基于高斯过程模型的语音增强[J]. 计算机工程, 2010, 36(5): 162-164.Shen Y, Zhang L Q. Speech enhancement based on gaussian process model[J]. Computer Engineering, 2010, 36(5): 162-164. |
| [2] | Cheng G, Guo L, Zhao T Y, et al. A more effective speech enhancement algorithm under non-stationary noise environment[J]. Journal of Northwestern Polytechnical University, 2010, 28(5): 668-672. |
| [3] | 熊志伟, 全海燕, 周荣强. 基于Bessel函数展开的ICA语音增强[J]. 计算机工程, 2013, 39(3): 311-315.Xiong Z W, Quan H Y, Zhou R Q. Independent component analysis voice enhancement based on Bessel function expansion[J]. Computer Engineering. 2013, 39(3): 311-315. |
| [4] | 叶利剑, 黄松华, 邱小军. 基于短时谱分析的语音增强改进算法[J]. 电声技术, 2011, 35(9): 42-46.Ye L J, Huang S H, Qiu X J. Improved speech enhancement algorithm based on short-time spectral analysis[J]. Audio Engineering, 2011, 35(9): 42-46. |
| [5] | 周璇, 鲍长春, 夏丙寅, 等. 一种基于自适应噪声估计的宽带语音增强算法[J]. 信号处理, 2011, 27(9): 1313-1318.Zhou X, Bao C C, Xiao B Y, et al. A wideband speech enchancement method based on adaptive noise estimation[J]. Signal Processing, 2011, 27(9): 1313-1318. |
| [6] | Xie W S, Yang G K. An adaptive speech signal de-noising algorithm based on estimation of scaled noise energy[J]. Journal of Shanghai Jiaotong University, 2012, 46(9): 1445-1449. |
| [7] | Huang J J, Zhang X W, Zhang Y F, et al. Single channel speech enhancement via time-frequency dictionary learning[J]. Acta Acoustics, 2012, 37(5): 30-38. |
| [8] | Benesty J, Chen J, Habets E L A P. Speech enhancement in the STFT domain[M]. Berlin, Germany: Springer, 2012: 53-66. |
| [9] | Hao J, Lee T W, Sejnowski T J. Speech enhancement using Gaussian scale mixture models[J]. IEEE Transactions on Audio, Speech and Language Processing, 2010, 18(6): 1127-1136. |
| [10] | Guo S N, Cui H J, Tang K. Speech enhancement based on short-time spectral amplitude estimates in low SNR[J]. Journal of Tsinghua University, 2010, 50(1): 149-152. |
| [11] | Dawes R L. Quantum neurodynamics: Neural stochastic filtering with the Schroedinger equation[C]//Proceedings of International Joint Conference on Neural Networks. Piscataway, NJ, USA: IEEE, 1992: 133-140. |
| [12] | Behera L, Kar I. Quantum stochastic filtering[C]//Proceedings of the 2005 IEEE International Conference on Systems, Man and Cybernetics. Piscataway, NJ, USA: IEEE, 2005: 2161-2167. |
| [13] | Behera L, Kar I, Elitzur A C. Recurrent Quantum neural network and its applications[M]//The Emerging Physics of Consciousness. Berlin, Germany: Spring, 2006: 327-350. |
| [14] | Behera L, Sundaram B. Stochastic filtering and speech enhancement using a recurrent quantum neural network[C]//Proceedings of International Conference on Intelligent Sensing and Information Processing. Piscataway, NJ, USA: IEEE, 2004: 165-170. |
| [15] | Zhu R X, Wu L N. Quantum stochastic filters for nonlinear time-domain filtering of communication signals[J]. Journal of Southeast University: English Edition, 2007, 23(1): 22-25. |
| [16] | Gandhi V, Arora V, Behera L, et al. EEG denoising with a recurrent quantum neural network for a brain-computer interface[C]//Proceedings of International Joint Conference on Neural Network. Piscataway, NJ, USA: IEEE, 2011: 1583-1590. |
| [17] | Gandhi V, Arora V, Behera L, et al. A recurrent quantum neural network model enhances the EEG signal for an improved brain-computer interface[C]//Proceedings of IET Seminar on Assisted Living 2011. Piscataway, NJ, USA: IEEE, 2011: 1-6. |
| [18] | Gandhi V, Prasad G, Coyle D, et al. Quantum neural network-based EEG filtering for a brain-computer interface[J]. IEEE Transactions on Neural Networks and Learning Systems, 2013, 25(2): 278-288. |
| [19] | 西蒙·霍金. 神经网络与机器学习[M]. 第三版. 北京: 机械工业出版社, 2011.Haykin S. Neural Networks and Learning Machines[M]. 3rd ed. Beijing: China Machine Press, 2011. |
| [20] | 况晓静, 吴先良, 黄志祥, 等. 基于FDTD方法求解含时薛定谔方程[C]//陕西西安: 中国电子学会, 2009: 990-993. |



