文章快速检索  
  高级检索
引用本文
刘明, 华亮. 广义切线混沌优化算法及其应用[J]. 信息与控制, 2015, 44(5): 604-611,627
LIU Ming, HUA Liang. Generalized Tangent-Chaos Optimization Algorithm and Its Application[J]. INFORMATION AND CONTROL, 2015, 44(5): 604-611,627.
广义切线混沌优化算法及其应用
刘明, 华亮    
南通大学电气工程学院, 江苏南通 226019
收稿日期: 2014-08-13; 录用日期: 2015-03-17; 修回日期: 2014-11-19
基金项目: 国家自然科学基金资助项目（61305031，51307089）；江苏省大学生创新创业训练计划重点项目（201410304023Z）；南通市科技计划项目（BK2014075）.
作者简介: 刘明（1981-），男，硕士，讲师．研究领域为群智能控制理论，神经网络，船舶电力系统．
华亮（1979-），男，博士，副教授．研究领域为图像处理与模式识别和机器人控制．
通讯作者: 刘明，liumingsongliuming@126.com
摘要：针对群体智能算法理论基础、缺乏普遍意义的理论分析等问题，提出了一种高性能的广义切线混沌优化算法（GTC）．该算法是基于空间域搜索的寻优算法，利用广义切线法、混沌算子和空间域搜索的特性来提高算法的全局寻优能力和收敛速度．为验证该算法的性能，与非线性递减权重粒子群算法（NDWPSO）、人工鱼群算法（AFSA）和实数编码的遗传算法（GA）进行对比，分别对3个测试函数、PID参数整定和一个高度非线性系统参数估计三个实例进行分析比较．研究结果表明，所提出的广义切线混沌算法具有大范围搜寻空间内的全局优化能力和快速收敛性．
关键词： 群体智能算法     广义切线法     混沌算子     参数优化    
Generalized Tangent-Chaos Optimization Algorithm and Its Application
LIU Ming, HUA Liang     
School of Electrical Engineering, Nantong University, Nantong 226019, China
Abstract:The theoretical foundation of swarm intelligence algorithms is relatively weak, and a general theoretical analysis has not yet been conducted. Thus, this study proposes a high-performance generalized tangent-chaos (GTC) optimization algorithm based on the spatial domain. In the algorithm, characteristics of the generalized tangent method, chaos operator, and searching in the spatial domain are applied to enhance the global search ability and convergence speed. To verify the performance of the GTC optimization algorithm, it is compared with the nonlinearly decreasing weight PSO, artificial fish school algorithm, and real-coded genetic algorithm. Three well-known benchmark functions, the tuning of PID controller parameters, and the parameter estimation of a highly nonlinear system are utilized to test the ability of the GTC optimization algorithm. Results show that the proposed GTC optimization algorithm has excellent global optimization performance and convergence speed.
swarm intelligence algorithm     generalized tangent method     chaos operator     parameter optimization    

1 引言

现实生活中许多控制领域的重要问题都涉及到寻优问题，如PID控制参数寻优、 非线性系统的结构辨识等. 这些问题都可以归纳为求解最大值或最小值的问题，传统优化算法有线性规划[1]、 整数规划[2]、 非线性规划[3]和动态规划[4]. 这些算法相对复杂，一般应用于解决小规模问题，不适合解决复杂优化问题[5]. 群体智能优化算法的出现为复杂寻优问题的求解提供了新的思路和方法，目前群体智能优化算法主要有遗传算法(GA)[6]、 粒子群算法(PSO)[7, 8, 9]、 人工鱼群算法(AFSA)[10]、 蚁群算法(ACA)[11]等. 文[6]提出一种遗传算法和混沌算子相结合的优化算法，利用混沌算子构建风速预测模型，使得模型更贴近现实； 利用遗传算法对混沌算子参数进行优化，提升预测性能. 文[7]提出了一种改进的自适应变异和动态惯性权重的PSO算法，并成功应用到动态系统的参数评估中. 文[8]提出一种新支配关系——ε优势支配，该支配下的最优粒子保留策略构建了一类多目标量子行为粒子群优化算法的总体构架，并成功地应用到求解输电网规划问题中. 文[10]提出了一种免疫人工鱼群网络算法，应用改进的觅食行为，提升算法的局部寻优能力； 采用免疫网络调节机理，保持人工鱼群多样性； 执行模式搜索法完成精英人工鱼群的精细搜索. 文[11]提出了一种改进的蚁群算法，利用方向信息素刻画寻优过程的全局信息、 提高解的全局性、 加快算法的收敛. 大量研究表明，群体智能优化算法具有并行式搜索、 有指导的随机搜索、 通用性强和智能性等优点，但该类算法也存在一些不足之处，如对问题依赖性较大，种群个体长度过长(搜寻空间维数较大)或个体中元素取值范围太大(搜寻空间范围较广)时难收敛和易陷入局部极值点等问题.

借鉴群体智能算法、 切线法和混沌算子思想，本文提出一种广义切线混沌优化算法. 广义切线法引入使得该算法具有较强的局部寻优能力，提高了算法的收敛速度，混沌算子的引入保持了种群多样性，使得粒子阶段信息得到极大的利用，提高了算法的全局搜索能力和收敛速度. 最后通过3个测试函数、 PID参数整定和一个高度非线性系统参数估计三个实例验证了所提算法的可行性和有效性.

2 广义切线混沌优化算法 2.1 广义切线法

考虑用曲线弧一端的切线来代替曲线弧，从而求出方程实根的近似值，这种方法叫做切线法[12]. 切线法一般用于求解2阶收敛速度的非线性方程. 其计算递推公式如式(1)所示：

式中，n为迭代次数，一定条件约束下只要n取值足够大，方程f(x)=0就能够获得精确的近似解. 对该方法进行引申，可获得引理1.

引理1 设f(x)在[a，b]上具有1阶导数，且对该区间上任意一点ξ有f(ξ)≥0，对区间上任意一点ξ1(f′(ξ1)为有限值且f′(ξ1)≠0)作切线，与x轴交点坐标为ξ2，那么由ξ1和ξ2构成的新区间内至少存在一点ξ3使得f(ξ3)<f(ξ1).

证明 假设ξ2<ξ1，在端点(ξ1，f(ξ1))的切线方程为y-f(ξ1)=f′(ξ1)(x-ξ1)，令y=0，则可得到切线与x轴交点坐标，由ξ2<ξ1可得f′(ξ1)>0. 根据导数定义可知，当ξ3→ξ1，有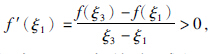所以有f(ξ3)<f(ξ1)，同理可证，当ξ2>ξ1时，该引理成立.

引理1讨论的是一元函数，引申到多元函数，即是本文提出的广义切线法，设F(x1，x2，…，xn)为n维空间函数且有F(x1，x2，…，xn)≥0，对于空间中存在偏导数且偏导数不全为零的任意一点(x1，x2，…，xn，F(x1，x2，…，xn))作切面，与y=0相交，交线(面或空间)上任意一点(xp1，xp2，…，xpn，0)与切点的连线即为广义切线，点(xp1，xp2，…，xpn，0)与点(x1，x2，…，xn，0)构成的新区域，则该区域内至少存在一点使得该点对应的函数值比切点对应的函数值小.

根据广义切线定义，如果优化问题的目标函数是求解极小值(或可以转换为求解极小值)，把该方法运用到寻优求解中有如下优点： 简单性、 初始化和寻优过程简单； 含确定性搜索的方法，新区域含有数值减小点； 种群的收敛速度快，局部寻优能力强； 靠近极小值点时能保证一定的收敛速度； 跳出局部极值点概率大，具有较强的全局寻优能力.

2.2 混沌算子

混沌是一种普遍的非线性现象，行为复杂类似随机，具有随机性、 遍历性、 规律性和敏感性. 鉴于混沌的这些特性，利用混沌算子进行优化搜索比盲目无序的随机搜索更具优越性，能够避免演化算法陷入局部最优点，混沌优化算法是一种全局性的优化算法.

首先采用混沌序列初始化种群，可使粒子分布较均匀，粒子分散性较好，为全局搜索多样性奠定基础[13]； 其次，单次迭代过程中，广义切线法产生的新搜索区域，利用混沌序列产生新粒子，可使粒子不重复遍布整个新区域，提高粒子利用的信息度，粒子多样性既提高粒子局部极值点的收敛速度，又提高粒子跳出局部最优点的概率性，从而实现全局寻优； 最后，在寻优过程中，防止粒子早熟停滞现象出现，利用有效判断方法，发现早熟迹象，利用混沌序列随机产生粒子替代对应粒子，使其跳出局部最优.

混沌映射一般有如下几种形式： 2维cat映射[14]、 logistic映射[15]、 tent映射[16]等，其中logistic映射方程[9]如式(2)所示：

其中，xn是变量x在第n步迭代时数值，初始值x0∈(0，1)，0.25、0.5和0.75除外；u是混沌映射的控制参数，当u=4时，logistic映射方程进入完全混沌状态[17].

2.3 广义切线混沌算法

广义切线混沌优化算法可以归类为群体智能优化算法，相比一些常见群体智能优化算法，该算法更强调个体在寻优过程中能力. 广义切线混沌优化算法的基本思想是： 用分布搜索优化空间中的点来模拟自然界中个体，利用混沌算子初始化个体，提高个体的多样性； 将个体进化过程类比为搜索最优解的过程，为提高个体寻优能力，单位步长内，个体寻优区域不再是一个点而是按照一定规律构造的新空间区域，提高个体寻优的信息度； 个体对环境的适应能力用目标函数(求解极小值形式)来表达，根据优胜劣汰选择机制用好的可行解代替差的可行解，并且在整个寻优过程中引入复制、 变异机制，整个群体将逐步向最优解靠近.

广义切线混沌优化算法的具体实现步骤如下：

步骤1 初始化广义切线混沌算法参数. 设定种群大小M，搜索空间维数D，迭代次数N，搜索空间范围分别表示为ID=[imin1，imin2，…，iminD]，FD=[fmax1，fmax2，…，fmaxD]，混沌算子初始值x0，迭代次数NC，混沌映射的控制参数，目标函数相关参数，新空间区域相关参数.

步骤2 采用混沌算子产生初始的个体位置Xi=[x1i，x2i，…，xDi](1≤i≤M).

步骤3 根据适应度函数计算个体的适应度值，并把适应度值作为当前个体的极值pBest(记为pi=[p1i，p2i，…，pDi])，找出当前适应度最小值作为整个种群最优解gBest(记为gi=[g1i，g2i，…，gDi]).

步骤4 计算个体的交点位置. 计算个体交点的方法有如下4种形式：

1)个体Xi=[x1i，x2i，…，xDi]，如果x1i，x2i，…，xDi的数值对个体的极值影响都是相互独立的且对应的适应度值分别为Y1i，Y2i，…，YDi，则根据文[12]，交点Xqi可用下式计算获得

由式(3)可知，当个体内元素之间相互独立时，个体位置的更新也将是独立运算，故个体空间维数的大小对算法的寻优影响较小，即此种情况下广义切线混沌算法有降维的作用.

2) 个体Xi=[x1i，x2i，…，xDi]，如果x1i，x2i，…xDi的数值对个体的极值影响都是相互影响的，没有独立的个体元素，设个体Xi的偏导数分别为fx1i，fx2i，…，fxDi，对应极值为Yi，则其中一个交点Xqi可用下式求解获得且Xqi=[xq1i，xq2i，…，xqDi]：

证明 设曲面(空间)方程：

函数f(x1，x2，…，xD)的偏导数fxi(x1，x2，…，xD)1≤i≤D在点(x10，x20，…，xD0)连续且不全为零.

令F(x1，x2，…，xD，y)=f(x1，x2，…，xD)-y，则：

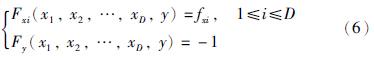
曲面(空间)(5)在点(x10，x20，…，xD0，y0)处的法向量为n=[fx1，fx2，…，fxD，-1]，则该点的切面方程为

则切面方程(7)与y=0的交线(面或空间)方程为

此外，在y=0面(空间)内过点(x10，x20，…，xD0)且与切面(7)垂直的直线方程可以表示为

式(8)和式(9)结合获得一个交点，该交点在交线(面或空间)上，故式(4)成立.

3) 个体Xi=[x1i，x2i，…，xDi]，如果x1i，x2i，…，xDi在对个体的极值影响上有些是相互独立的，有些是相互影响的，则把个体中的这些元素进行分组，分别按1)和2)中方法进行处理.

4) 如果个体Xi=[x1i，x2i，…，xDi]在某点不可导，交点采用随机产生方式获得.

步骤5 根据上述交点和切点构建新的搜索空间区域. 利用混沌算子在新的区域进行寻优，计算个体极值，并更新个体极值和全局极值.

步骤6 复制和变异. 按照一定的概率对群体中性能较好的个体进行复制和性能差的个体进行变异.

步骤7 判断是否达到最大迭代次数或优化的终止条件，如达到则此次循环终止，输出搜索结果，否则返回步骤4.

广义切线混沌优化算法并不严格要求优化对象连续可导，对有限的不可导点该算法同样适用，对于不可导点空间域的构建采用随机产生方式，增加个体的多样性，提高全局寻优能力.

由上文分析可知，空间域的构建、 复制和变异概率影响算法的全局寻优能力和收敛速度，其中空间域的构建是关键. 参数取值大使搜索范围变广，能够提高跳出局部极值点的概率和全局寻优能力，在一定取值范围内能够加快收敛速度，但也会使局部收敛能力变弱，降低搜索结果的精度； 参数取值小使搜索范围变小，能够提高局部寻优能力，加快局部收敛速度，提高搜索结果精度，但会降低全局寻优能力.

3 Benchmark函数测试 3.1 Benchmark函数

Benchmark函数被大量用于优化问题求解算法的验证，其中一些函数很难求得全局最优解，本文选其中3个作为测试函数，分别是Schaffer函数[18]、 Rastrigin函数[19]和Schwefel函数[20].

1) Schaffer函数

这是一个复杂的多模函数，全局最优点位于一个狭窄的区域内，而距离全局最优点大约3.14的范围内存在无限多个局部最优点，函数强烈震荡特性使得很难收敛于全局最优. 该函数全局最优值为0.

2) Rastrigin函数

这是一个多峰值函数，具有大量按正弦拐点排列的、 很深的局部最优点，优化算法容易在通往全局最优点的路径上陷入一个局部最优点[19]. 该函数全局最优值为0.

3) Schwefel函数

这是一个典型的欺骗问题，有1个全局极小值点，在(420.968 7，420.968 7，…，420.968 7)处，距离另一个局部最优点很远，如果陷入局部最优就很难跳出，极小值为-418.982 9n，n为变量个数.

3.2 性能测试

为验证文中提出的GTC算法寻优能力，对3.1节中的3个Benchmark函数分别采用GTC算法、 NDWPSO算法、 AFSA算法和GA算法进行寻优计算和分析比较. 所有仿真实验种群数为40，Schaffer函数和Rastrigin函数本身作为各算法适应值的计算公式，全局最优值为0，而Schwefel函数加上420作为各算法的适应值计算公式，全局最优值为1.017 1n. 为验证算法的收敛速度，当个体元素取值范围相等情况下，对同一个Benchmark函数各个算法的迭代次数设置一致或等效一致(个体计算次数等效一致)，为验证算法的适应性，对同一个Benchmark函数，当个体元素取值范围变化时，各个算法的参数设置不变.

GA算法中复制概率PC设为0.7，变异概率Pm设为0.1.

NDWPSO算法中非线性递减惯性权重公式如下[11]：

式中itermax为最大迭代次数，iter为当前迭代次数，本文n取值1.2，Schaffer函数和Rastrigin函数设置ωmax、 ωmin分别为1和0.4，Schwefel函数设置ωmax、 ωmin分别为1.2和0.2，学习因子C1=C2=2.

AFSA算法中尝试次数取50，拥挤度因子取0.318.

GTC算法中混沌映射采用logistic映射，混沌控制参数u=4.

3个Benchmark函数的性能测试结果如表 1~4所示.

表 1 Schaffer函数测试结果 Tab. 1 Test results of Schaffer function
个体元素取值范围 GA NDWPSO AFSA GTC
迭代次数 均值 迭代次数 均值 迭代次数 均值 迭代次数 均值
0～1 400 7.16E-6 400 0 40 4.320E-4 10 0
0～10 400 9.33E-3 400 0 40 3.616E-3 10 0
0～100 400 2.29E-2 400 0 40 0.164 856 10 0
表选项
表 2 Schwefel函数测试结果 Tab. 2 Test results of Schwefel function
个体元素
取值范围		 个体元素
长度		 GANDWPSOAFSAGTC
迭代次数均值迭代次数均值迭代次数均值迭代次数均值
0～500101 00010.596 381 0001 060200700.328 502510.350 41
203 50023.399 283 5003 0507002 030.148 008821.460 22
307 00047.228 857 0005 3501 4003 331.832 0017532.543 55
400～500101 00010.208 871 00010.220010.514 902510.275 14
203 50020.510 483 50020.470036.687 658821.279 68
307 00031.129 107 00030.61 40081.762 4417532.519 72

表选项
表 3 Rastrigin函数测试结果 Tab. 3 Test results of Rastrigin function
个体元素
取值范围		 个体元素
长度		 GANDWPSOAFSAGTC
迭代次数均值迭代次数均值迭代次数均值迭代次数均值
0～5101 0002.399 5481 0000.001 5762000250
203 50011.598 2903 5000.189 02170033.080 3880
307 00036.678 6107 0000.727 6121 400104.670 81750
0～50101 00015.621 3601 0000.160 9122000250
203 50055.430 1203 50013.597 730700136.127 9880
307 000171.219 3007 00065.305 4301 400507.910 51750

表选项
表 4 算法运行时间(单位： s) Tab. 4 Runtime of algorithms (unit： s)
测试函数个体元素取值范围个体元素长度GANDWPSOAFSAGTC
Schaffer 0～120.287 0000.178 3920.406 7360.009 296
0～1020.288 0000.178 2960.693 0470.013 960
0～10020.290 0000.195 3740.671 2340.012 634
Schwefel 0～500100.640 4510.464 2253.217 0660.438 667
0～500202.371 9211.840 22222.310 5601.709 782
0～500305.126 1494.178 18351.347 5403.902 611
400～500100.622 0370.466 8813.756 9620.448 355
400～500202.364 8751.838 47120.256 1501.760 146
400～500305.116 2014.112 35849.770 3103.791 931
Rastrigin0～5100.448 9010.219 7016.454 4760.137 080
0～5201.690 6150.897 21926.544 4700.563 471
0～5303.673 6252.556 44354.122 6001.318 838
0～50100.447 4380.280 3543.218 9690.133 836
0～50201.690 7130.894 78011.977 8400.564 674
0～50303.664 6112.564 32923.494 2301.317 972

表选项

由表 1可知，NDWPSO算法和GTC算法都能收敛于全局最优值0，AFSA算法和GA算法收敛于全局最优值附近，受个体元素取值范围的影响(特别是AFSA算法)，个体元素取值范围越广寻优结果离全局最优值点越远. 从表 4算法运行时间可以看出，GTC算法明显优于其它3种算法，AFSA算法耗时最长.

由表 2可知，当个体元素取值范围为400～500时，NDWPSO算法、 GTC算法和GA算法寻优结果相差较小，此时AFSA算法受个体元素长度影响较大. 当个体元素取值范围为0～500时，GTC算法寻优结果最好，其它3种算法不同程度受个体元素长度的影响，其中NDWPSO算法和FSA算法寻优结果严重偏离全局最优值点，算法不收敛. 从表 4算法运行时间可以看出，GTC算法耗时略优于NDWPSO算法和GA算法，而AFSA算法耗时远大于其它3种算法.

由表 3可知，只有GTC算法收敛于全局最优值点，其它3种算法受个体元素取值范围和个体元素长度影响较大，随着体元素取值范围变广和个体元素长度变长，这3种算法都出现不收敛现象. 从表 4算法运行时间可以看出，GTC算法要优于其它3种算法，AFSA算法耗时远大于其它3种算法.

综上分析可以得出： 个体元素取值范围、 个体元素长度和迭代次数都对寻优结果具有一定程度的影响. GTC算法的适应性最好，个体元素的取值范围对其影响几乎可以忽略不计，这也是该算法的一个巨大优势，即具有大范围的寻优能力，而其它3种算法对个体元素的取值范围较敏感，范围取的太广可能导致寻优结果与全局最优值偏差较大. 4个算法中对个体元素长度的敏感性最小的仍然是GTC算法，其它3种算法受影响较大，随着个体元素长度的增加需要更大的迭代次数进行全局寻优，否则很难收敛，有些情况下即使增加迭代次数也难以收敛. 单纯从迭代次数上看，GTC算法的收敛迭代次数要少的多，这主要是由于GTC算法的寻优计算是基于空间区域，其它3种算法的寻优计算是基于点，故GTC算法的计算包含信息量要大的多，非常有利于算法收敛.

上述研究同时也表明，由于GTC算法单位迭代步长内在空间域内搜索，因此算法在单位迭代步长内具有较高的搜寻信息量，但同时也增加了算法的计算量，不过该问题可以通过较少的迭代次数进行弥补.

4 PID控制参数优化整定 为验证GTC算法在PID控制器参数优化中的寻优能力，对以下对象[21]进行了仿真分析：

本节分别采用GA算法、 NDWPSO算法、 AFSA算法和GTC算法整定PID控制器参数，比较对象的阶跃响应控制效果. 所有仿真实验种群数为40，PID的3个控制参数取值范围见表 5，误差平方和作为适应值函数. 为验证算法的收敛速度，当个体元素取值范围相等情况下，各个算法的迭代次数设置一致或等效一致(个体计算次数等效一致)，为验证算法的适应性，当个体元素取值范围变化时，各个算法的参数设置不变.

表 5 PID控制器的测试指标 Tab. 5 Index testing of PID controller
个体元素取值范围 GA NDWPSO AFSA GTC
KPKIKD迭代次数均值迭代次数均值迭代次数均值迭代次数均值
0～200～10～15001.237 4765001.389 5362001.327131.238 172
0～200～100～10500674.937 6500219.036 7200126.875 4131.244 776

表选项

GA算法中，复制概率PC=0.9，变异概率Pm=0.1.

AFSA算法中尝试次数取100，拥挤度因子取0.618.

NDWPSO算法中非线性递减惯性权重公式采用式(13)，n=1.2，ωmax=1，ωmin=0.4，学习因子C1=C2=2.

GTC算法中混沌映射采用logistic映射，混沌控制参数u=4，复制概率PC=0.9，变异概率Pm=0.2.

表 5中测试指标值为每种算法随机运行25次的平均值，从表 5的计算结果可以看出： 个体元素取值范围对寻优结果具有一定程度的影响. 当个体元素取值范围较小时，4种算法的寻优结果差别较小，即都能够寻找到全局最优点值或全局最优点附近值，NDWPSO算法和AFSA算法寻优结果相比其它两种算法稍微差一点，这也说明对于PID控制参数，只要参数范围选取得当，各种寻优算法都可以取得较好的寻优结果. 当个体元素取值范围较大且各个算法的参数设置不变情况下，只有GTC算法的平均适应值在较理想的范围内，说明GTC算法的适应性强，个体元素的取值范围对其影响几乎可以忽略不计，这也是该算法的一个巨大优势，再次证明该算法具有大范围的寻优能力，而其它3种算法对个体元素的取值范围较敏感，范围取的太广可能导致寻优结果与全局最优值偏差较大.单纯从迭代次数上看，GTC算法的收敛迭代次数要少的多，这主要是由于GTC算法的寻优计算是基于空间区域，其它3种算法的寻优计算是基于点，故GTC算法的计算包含信息量要大的多，有利于算法收敛.

图 1～4为3种算法针对PID控制参数寻优25次寻优历程的波形图.4个图中波形1都是指个体元素取值范围较小时的寻优结果，波形2都是指个体元素取值范围较大时的寻优结果.

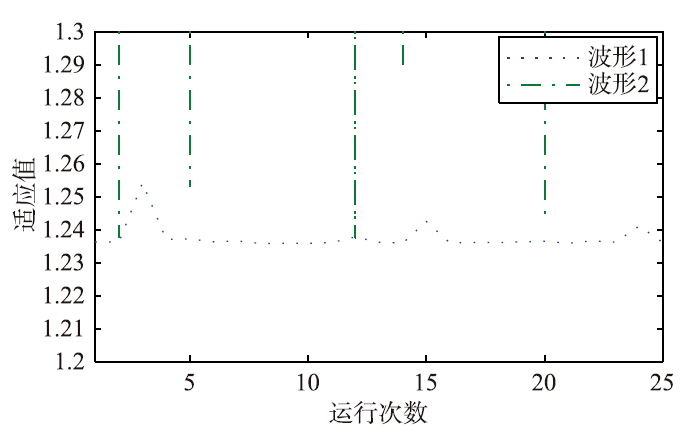图 1 GA算法寻优历程Fig. 1 Optimization process of the GA algorithm
图选项
图 2 AFSA算法寻优历程Fig. 2 Optimization process of the AFSA algorithm
图选项
图 3 NDWPSO算法寻优历程Fig. 3 Optimization process of the NDWPSO algorithm
图选项
图 4 GTC算法寻优历程Fig. 4 Optimization process of the GTC algorithm
图选项

从图 1～4可以看出： 总体而言，GTC算法的波形波动性最小，当个体元素取值范围较小时，GTC算法和GA算法波形波动性较NDWPSO算法和AFSA算法波形波动性低. 而当个体元素取值范围较大时，NDWPSO算法、 AFSA算法和GA算法波形波动性比GTC算法的波形波动性要大得多，如果以[1.2，1.3]为求得最优解或近似最优解的成功率范围，则GTC算法成功率为100％，NDWPSO算法成功率为24％，GA算法成功率为20％，AFSA算法成功率为40％. 上面分析再次表明GTC算法的可靠性较高. 同时图 1～4也表明GTC算法的适应性较强，受个体元素取值范围影响最小，具有较好的收敛性.

5 非线性系统参数辨识

为验证GTC算法在系统参数辨识应用中的寻优性能，对以下不稳定非线性系统[7]进行了仿真分析：

本节分别采用GA算法、 NDWPSO算法、 AFSA算法和GTC算法对上述参数a1、 a2、 a3、 a4进行辨识，分别采用平均值和均方误差评估辨识效果. 所有仿真实验种群数为40. 为验证算法的收敛速度，在个体元素取值范围相等情况下，各个算法的迭代次数设置一致或等效一致(个体计算次数等效一致)，NDWPSO算法和GA算法迭代次数为2 000，AFSA算法迭代次数为1 000，GTC算法迭代次数为50，为验证算法的适应性，当个体元素取值范围变化时，各个算法的参数设置不变.

GA算法中，PC=0.9，Pm=0.1.

AFSA算法中尝试次数取50，拥挤度因子取0.318.

NDWPSO算法中非线性递减惯性权重公式采用式(13)，n=1.2，ωmax=0.9，ωmin=0.4，学习因子C1=C2=2.

GTC算法中混沌映射采用Logistic映射，混沌控制参数u=4，复制概率PC=0.9，变异概率Pm=0.1.

从表 6计算结果比较可以看出： 总体而言GTC算法的参数辨识寻优结果最好，只有当个体元素取值范围为0～2时，参数a3的MSE值和参数a4的MSE值及均值较GA算法参数辨识寻优结果略差. GA算法、 AFSA算法和NDWPSO 算法参数辨识寻优结果受个体元素取值范围影响较大，如当参数取值0～100时这3种算法全部不收敛，而GTC算法受影响微乎其微，表明GTC算法具有大范围空间寻优能力，其适应性强、 可靠性高. 其次表中参数辨识结果GTC算法只需要很少的迭代次数，说明基于空间区域的搜寻算法具有收敛速度快的优势.

表 6 参数辨识结果分析Tab. 6 Analysis of parameter identification results
参数 个体元素
取值范围		 GA NDWPSO AFSA GTC
MSE均值MSE均值MSE均值MSE均值
a10～20.000 40.500 2560.172 20.411 8840.094 70.467 03200.500 000
0～200.006 60.502 1167.458 55.146 268--00.500 000
0～10056.691 747.587 350----00.500 000
a20～20.000 50.300 2160.149 30.220 6040.060 30.284 9320.000 20.299 968
0～200.010 50.304 21210.892 78.393 144--00.299 988
0～10051.246 739.319 080----00.299 984
a30～20.000 11.799 9480.000 41.799 9040.005 11.800 1640.000 21.800 020
0～200.001 01.800 5327.912 77.713 232--0.000 41.799 968
0～10057.352 150.862 000----0.000 51.799 916
a40～20.000 40.900 0560.016 50.891 3720.140 00.942 5560.003 90.899 492
0～200.022 70.906 3769.504 37.201 292--0.012 90.904 040
0～10055.767 648.394 600----0.013 00.896 516

表选项

图 5～8为4种算法在个体元素取值范围为0～2时针对非线性系统参数寻优25次寻优历程的波形图. 从4个波形图可以看出： GTC算法和GA算法的波形波动性最小，虽然NDWPSO算法在25次寻优过程中有17次获得全局最优值，其它3种算法只是获得全局最优附近值，然而GTC算法和GA算法波形波动性较NDWPSO算法波形波动性低，这是表 6中NDWPSO算法的参数辨识分析结果最差的主要原因，即NDWPSO算法在该实例中可靠性相对较弱. 所有波形中AFSA算法波形波动性最大，说明该算法在该实例中可靠性最差.

图 5～8为4种算法在个体元素取值范围为0～2时针对非线性系统参数寻优25次寻优历程的波形图. 从4个波形图可以看出： GTC算法和GA算法的波形波动性最小，虽然NDWPSO算法在25次寻优过程中有17次获得全局最优值，其它3种算法只是获得全局最优附近值，然而GTC算法和GA算法波形波动性较NDWPSO算法波形波动性低，这是表 6中NDWPSO算法的参数辨识分析结果最差的主要原因，即NDWPSO算法在该实例中可靠性相对较弱. 所有波形中AFSA算法波形波动性最大，说明该算法在该实例中可靠性最差.

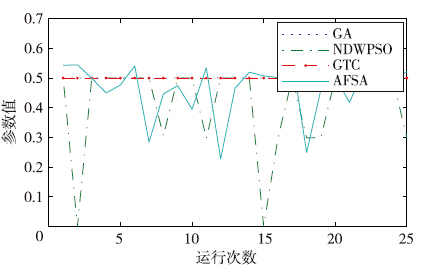图 5 参数a1寻优历程Fig. 5 Optimization process of a1
图选项
图 6 参数a2寻优历程Fig. 6 Optimization process of a2
图选项
图 7 参数a3寻优历程Fig. 7 Optimization process of a3
图选项
图 8 参数a4寻优历程Fig. 8 Optimization process of a4
图选项

当个体元素取值范围较大时，NDWPSO算法、 AFSA算法和GA算法数据波动性比GTC算法的波形波动性要大得多，如当个体元素取值范围为0～100时，3种算法都不收敛，而GTC算法依然能够收敛，寻优结果依然在全局最优点附近. 上面分析再次表明GTC算法的可靠性最高，表明GTC算法的适应性最强，受个体元素取值范围影响最小，具有较高的收敛性.

6 结束语

本文研究的广义切线混沌优化算法是一种基于空间域的群智能优化算法. 该算法融合了广义切线法和混沌算子的特性，使得该算法具有大范围搜寻空间内全局寻优能力，收敛速度快，可靠性高，特别在优化搜索空间未知或部分未知的对象参数，较其它算法具有一定优势，文中3个实例也验证了该算法的优越性. 文中对广义切线混沌优化算法进行了初步研究，算法尚需要进一步完善，如何构建新的搜寻空间区域，复制和变异概率取值等，进一步提高算法的优化能力.

参考文献
[1] Phan S H, Steve H. A review of the formulation and application of the spatial equilibrium[J]. Journal of Forestry Research, 2011, 22(4): 671-679.
[2] 于战科, 黄华军, 倪明放, 等. 求QoS路由的整数线性规划方法[J]. 系统工程理论与实践, 2013, 33(4): 1019-1023. Yu Z K, Huang H J, Ni M F, et al. A method of integer linear program for QoS routing problem[J]. Systems Engineering: Theory ＆ Practice, 2013, 33(4): 1019-1023.
[3] Liu M L, Pu D G, Li X Q. An inexact line search SQP-filter method for nonlinear programming problems[J]. Mathematica Application, 2011, 24(3): 532-539.
[4] Draguna V, Frank L. Adaptive dynamic programming for online solution of a zero-sum differential game[J]. Journal of Control Theory and Applications, 2011, 9(3): 353-360.
[5] 杨淑莹, 张桦. 群体智能与仿生计算Matlab技术实现[M]. 北京: 电子工业出版社, 2012: 1-12. Yang S Y, Zhang H. Matlab technology to implement the swarm intelligence and evolutionary computation[M]. Beijing: Publishing House of Electronics Industry, 2012, 1-12.
[6] Xiu C B, Guo F H. Wind speed prediction by chaotic operator network based on Kalman filter[J]. Science China Technological Sciences, 2013, 56(5): 1169-1176.
[7] Alfi A. PSO with adaptive mutation and inertia weight and its application in parameter estimation of dynamic systems[J]. Acta Automatica Sinica, 2011, 37(5): 541-549.
[8] 施展, 陈庆伟, 胡维礼. 一类多目标量子行为粒子群优化算法收敛性分析及应用[J]. 信息与控制, 2013, 42(4): 407-415. Shi Z, Cheng Q W, Hu W L. Convergence analysis of a class of multi-objective quantum-behaved particle swarm optimization algorithms and its application[J]. Information and Control, 2013, 42(4): 407-415.
[9] Li M W, Kang H G, Zhou P F, et al. Hybrid optimization algorithm based on chaos, cloud and particle swarm optimization algorithm[J]. Journal of Systems Engineering and Electronics, 2013, 24(2): 324-334.
[10] 邓涛, 姚宏, 杜军. 多峰函数优化的免疫人工鱼群网络算法[J]. 系统工程与电子技术, 2013, 35(2): 452-456. Deng T, Yao H, Du J. Immune artificial fish swarm network algorithm for multimodal function optimization[J]. Systems Engineering and Electronics, 2013, 35(2): 452-456.
[11] 孟祥萍, 片兆宇, 沈中玉, 等. 基于方向信息素协调的蚁群算法[J]. 控制与决策, 2013, 28(5): 782-786. Meng X P, Pian Z Y, Shen Z Y, et al. An algorithm based on direction-coordinating[J]. Control and Decision, 2013, 28(5): 782-786.
[12] 同济大学数学系. 高等数学[M]. 北京: 高等教育出版社, 2007: 178-181. University of Tongji-Mathematics Department. Higher mathematics[M]. Beijing: Higher Education Press, 2007, 178-181.
[13] 朱海梅, 吴永萍. 一种高速收敛粒子群优化算法[J]. 控制与决策, 2010, 25(1): 20-24. Zhu H M, Wu Y P. A PSO algorithm with high speed convergence[J]. Control and Decision, 2010, 25(1): 20-24.
[14] Kao Y T, Erwie Z. A hybrid genetic algorithm and particle swarm optimization for multimodal functions[J]. Applied Soft Computing, 2008, 8(2): 849-857.
[15] Lü X M, Huang K L, Guang Y. Optimizing strategy of system level fault diagnosis based on chaos particle swarm optimization[J]. Systems Engineering and Electronics, 2010, 32(1): 217-220.
[16] Sheng Y X, Pan H T, Xia L Y, et al. Hybrid chaos particle swarm optimization algorithm and application in benzene-toluene flash vaporization[J]. Journal of Zhejiang University of Technology, 2010, 38(3): 319-322.
[17] Li M S, Huang X Y, Liu H S, et al. Prediction of the gas solubility in polymers by a radial basis function neural network based on chaotic self-adaptive particle swarm optimization and a clustering method[J]. Journal of Applied Polymer Science, 2013, 130(5): 3825-3832.
[18] Gao Z, Liao X Z. Improved oustaloup approximation of fractional-order operators using adaptive chaotic particle swarm optimization[J]. Journal of Systems Engineering and Electronics, 2012, 23 (1): 145-153.
[19] 李丽, 牛奔. 粒子群优化算法[M]. 北京: 冶金工业出版社, 2009: 25-31.Li L, Niu B. Particle swarm optimization algorithm[M]. Beijing: Metallurgical Industry Press, 2007, 178-181.
[20] 贺毅朝, 张翠军, 王培崇, 等. 微粒子群算法与郭涛算法在数值优化中的比较[J]. 计算机工程与应用, 2007, 43(11): 100-103.He Y C, Zhang C J, Wang P C, et al. Comparison between particle swarm optimization and Guo Tao algorithm on function optimization problems[J]. Computer Engineering and Applications, 2007, 43(11): 100-103.
[21] 修志芳. 预测函数控制及其应用研究[D]. 浙江: 浙江大学, 2008.Xiu Z F. Research and application of predictive functional control[D]. Zhejiang: Zhejiang University, 2008.
"http://dx.doi.org/10.13976/j.cnki.xk.2015.0604"
中国科学院主管，中国科学院沈阳自动化研究所、中国自动化学会共同主办。
0

文章信息

刘明, 华亮
LIU Ming, HUA Liang
广义切线混沌优化算法及其应用
Generalized Tangent-Chaos Optimization Algorithm and Its Application
信息与控制, 2015, 44(5): 604-611,627.
INFORMATION AND CONTROL, 2015, 44(5): 604-611,627.
http://dx.doi.org/10.13976/j.cnki.xk.2015.0604

文章历史

收稿日期：2014-08-13
录用日期：2014-11-19
修回日期：2015-03-17

工作空间