1 引言
预测控制[1, 2](predictive control)便于处理时滞和有约束条件问题,在复杂工业过程中得到了广泛的应用[3, 4, 5]. 预测控制采用滚动优化的结构且每一步均为参数优化问题. 在线计算量直接关系到实际的控制品质,文[6]通过引进控制增量的期望衰减因子,使矩阵求逆运算变成数值的求逆运算,显著提高了系统的运算速度; 文[7]采用斐波那契序列方法,提出了一种针对双曲线时变约束系统的变步长预测控制算法,通过求解子优化问题来在线确定步长,在保证约束的前提下,具有在线计算量小、 速度快的优点; 文[8]采用双层结构,研究了多变量约束预测控制,稳态关联约束、 定值约束和区域约束条件分别作为等式约束和不等式约束,再将优化值传递给动态优化,在保证负荷跟踪速率的前提下,有效地减小了被控量和操作变量的波动.
解析塔是化工和炼油厂气体分离装置中重要的操作单元. 在气体分离工艺中其主要的作用是将干气脱硫过程中得到的富胺液进行脱硫处理,气体分馏装置生产工艺流程长、 设备多,解析塔的控制工艺程度直接影响到后续的脱丙烷塔等控制操作,所以解析塔的过程控制在气体分离工业中尤为重要. 在实际工业生产中,需要考虑多种约束条件,把无约束的控制器应用于实际存在约束的系统,将会降低闭环系统性能和产品收率[9, 10].
本文针对解析塔工业控制中需要满足工艺要求下的输入输出约束条件问题,提出一种基于二次插值法的约束预测控制算法. 结合阶梯式控制策略[11]将矩阵求逆运算简化为标量的优点,采用二次插值法[12, 13, 14]在约束区间内不断地使用二次多项式近似目标函数,并逐步用插值多项式的极小点来确定满足约束的控制增量的最优解,从而求得当前时刻的预测控制量,依托现场的实测模型,验证了本文算法的有效性.
2 阶梯式约束DMC(dynamic matrix control)优化算法 2.1 预测模型针对开环渐近稳定的SISO(single-input single-output)系统:
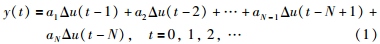
其中,y为输出变量,u为输入变量,Δu为控制增量,对象的单位阶跃响应的采样值为
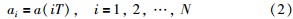
其中,T为采样周期; N为建模时域,这N个采样值反映出了系统的动态特性. 对于渐近稳定系统,当i→∞时,hi→0,aN近似为稳态值,权序列系数为hi=ai-ai-1. {a1,a2,…,aN}有限集合的参数构成了DMC的模型参数,尽管阶跃响应是一种非参数模型,但是由于线性系统的比例叠加性质,a(iT)足以预测模型的输出值[15].
考虑到系统在未来M个时刻的控制增量Δu(t),…,Δu(t+M-1)的作用下,系统在未来各时刻的预测模型输出为
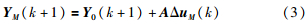
式中,
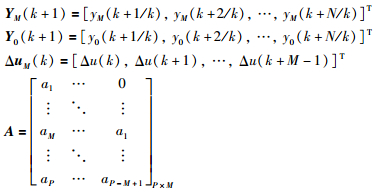
其中,A是由阶跃响应系数构成的系数矩阵; M为控制时域长度,P为预测时域长度,N为模型时域长度,为使问题有意义,通常M≤P≤N.
2.2 滚动优化选取二次型性能指标函数为
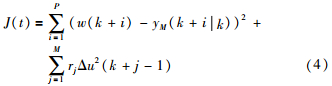
w(k)=[w(k+1),…,w(k+P)]T为期望输出值,r=diag(r1,…,rM)为控制权矩阵.
当工程实施时,出于增强算法鲁棒性的考虑,并且抑制Δu变化过于剧烈,使系统输出跟踪一条柔化曲线w(k),采用如下1阶指数形式[16]:
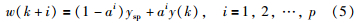
其中,ysp为设定值,a=exp(-Ts/Tp)为柔化系数,Ts为采样周期,Tp为参考轨迹时间常数.
为了减小DMC算法的在线计算量,引进阶梯式控制策略[8]:
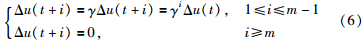
式中,Δu(t)为控制增量,γ为阶梯因子,因此可得:
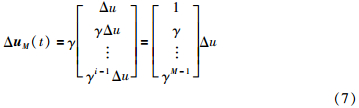
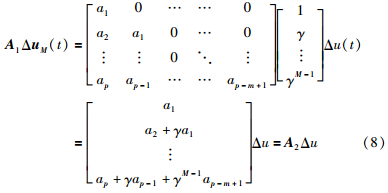
A2是p×1的列向量. 得到新的目标函数:
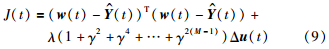
其中,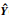 (t)为系统校正输出矩阵,w(t)为期望输出值. 在无约束的情况下,极小化目标函数,即dJ(t)/dΔu(t)=0,可得即时控制增量为
(t)为系统校正输出矩阵,w(t)为期望输出值. 在无约束的情况下,极小化目标函数,即dJ(t)/dΔu(t)=0,可得即时控制增量为
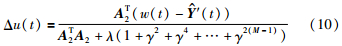
因阶梯式算法中把复杂的逆矩阵运算变成了数值运算,从而使计算量大为降低,系统响应速度加快,t时刻的预测控制量为
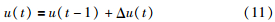
在生产实际中,由于阀门开度和产品工艺要求等因素,存在着多种约束:
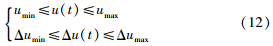
基于约束条件下的控制问题,可表示为求解有限时域优化问题:


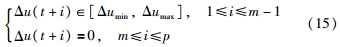
J(t)是式(4)中所示的性能指标,令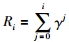 ,综合式(7)和式(14)、 (15). 控制增量Δu(t)的最终范围为
,综合式(7)和式(14)、 (15). 控制增量Δu(t)的最终范围为
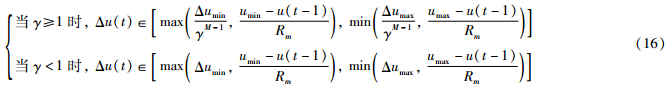
基于二次插值法的阶梯式DMC基本思路是: 在搜索区间中不断地使用二次多项式去近似目标函数,并逐步用差值多项式的极小值点来逼近目标函数. 首先用进退法[17]在约束区间内确定3个点s0、 s1、 s2(满足s0<s1<s2)和步长h,对应的函数值为J0、 J1和J2,满足J1<J0,J1<J2,则二次拉格朗日插值多项式为
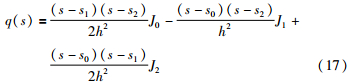
q(s)的1阶导数为
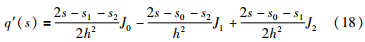
令q′(s)=0解得:
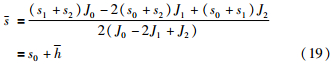
其中,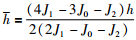 ,又q(s)的2阶导数为
,又q(s)的2阶导数为
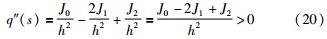
可知q(s)为凸二次函数,故smin是q(s)的全局极小点. 由于s=s0+h比s0更逼近s*(极小真值点),故可用、分别替代s0和h,之后重复上述计算过程,求出新的s和h. 重复这一迭代过程,直到得到所需的精度为止. 算法中二次插值多项式的极小点是用目标函数的导数隐式地确定的,算法的实现过程并不需要使用导数值,从而保证了在线优化的高效性.
基于二次插值法的阶梯式预测控制算法设计如下:
(1) 设计控制器离线参数: 控制增量加权系数r,预测步长p,控制步数m,阶梯因子β和精度要求L.
(2) 在线计算t时刻最优控制增量Δu′(t),步骤如下:
Step 1: 先由进退法确定出3个点s0、 s1、 s2(满足s0<s1<s2),则对应的目标函数值J0、 J1、 J2,满足J1<J0,J1<J2. k=1,设定容许误差ε<0.000 1.
Step 2: 若|s2-s0|<ε,停算,输出s*≈s1.
Step 3: 计算插值点. 根据式(18)计算s和=J(s). 若J1≤J,转Step 5否者转Step 4.
Step 4: 若s1>s,则s2=s1,s1=s,J2=J1,J1=J,转Step 2; 否则,s0=s1,s1=s,J0=J1,J1=J,k=k+1,转Step 2.
Step 5: 若s1<s,则s2=s,J2=J,转Step 2; 否则,J0=J,s0=s,k=k+1,转Step 2.
3 解析塔的工艺流程及建模为了验证本文算法的有效性,选取某石化公司的气体分离装置的解析塔作为研究对象. 其工艺流程为: 经胺加热器加热的富胺液流经闪蒸塔,将烃类蒸发出去,然后流入解析塔,解析塔塔底重沸器采用0.3 MPa蒸汽加热,温度控制在120 ℃左右,从而将富液中的H2S解析出去. 解析出的H2S气体从塔顶流出并经塔顶冷凝器冷凝,冷凝下的部分会形成酸性水全部用作内回流; 另一部分不凝气则进入H2S后冷却器,最终进入硫化氢分离罐. 而解析后的贫胺液经换热器、 冷却器,冷却至40 ℃以下进入胺储罐循环使用,从而实现硫化氢与胺液的分离.
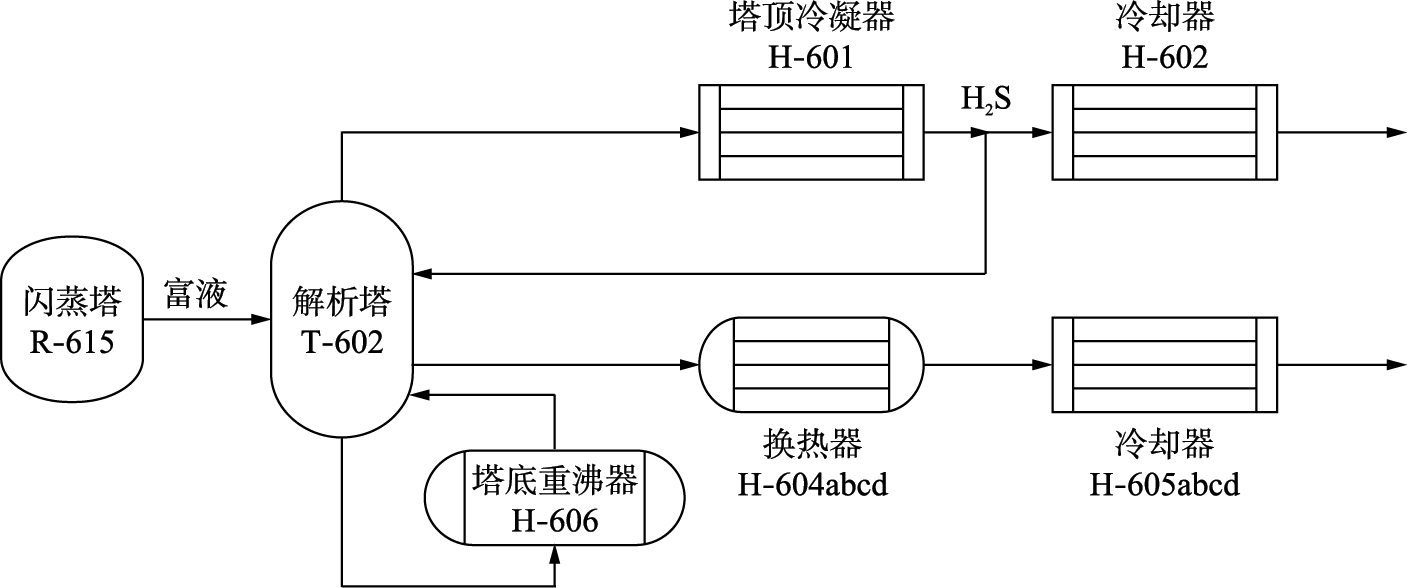 |
| 图 1 解析塔工艺流程图 Fig. 1 Flow chart of analytic tower |
采用经典的阶跃响应法获得系统的数学模型[18, 19, 20],塔底温度回路的传递函数:

塔底温度回路为开环渐近稳定的SISO系统,塔底温度为被控对象,采用2.1节预测模型,y为输出变量. 由于考虑到产品工艺要求,系统控制量u及Δu需要满足的约束条件如下:
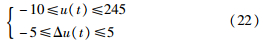
本文算法的控制参数如下: 阶梯因子γ=1,参考轨迹柔化系数β=0.95,控制增量加权系数γ=0.95,模型长度取N=100,算法的精度要求取L=0.000 1. 分别采用直接截断法和二次插值法的阶梯式DMC算法跟踪给定值仿真比较结果如图 2和图 3所示. 两者同取预测步长p=30,优化步长为m=20.
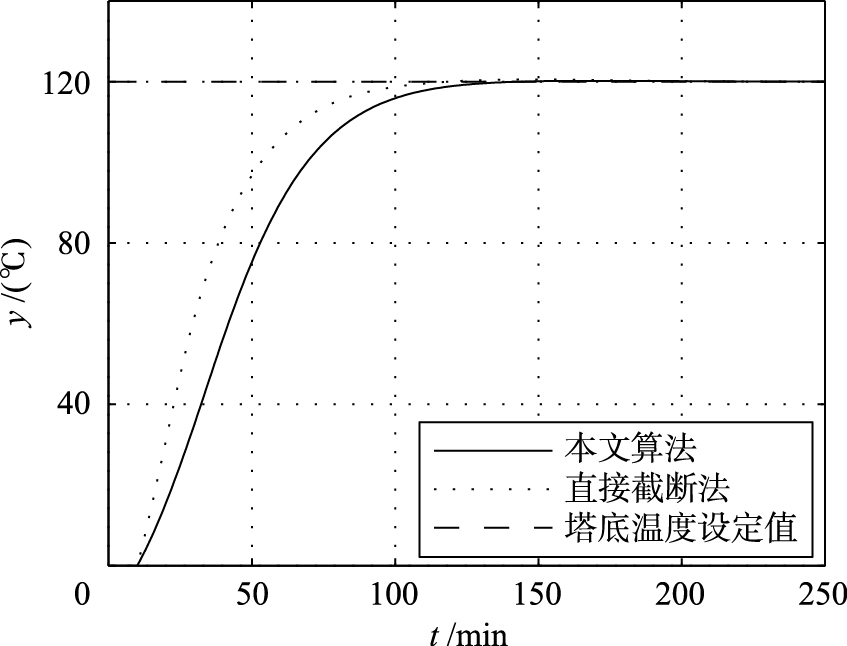 |
| 图 2 塔底温度输出曲线 Fig. 2 The output curves of tower bottom temperature |
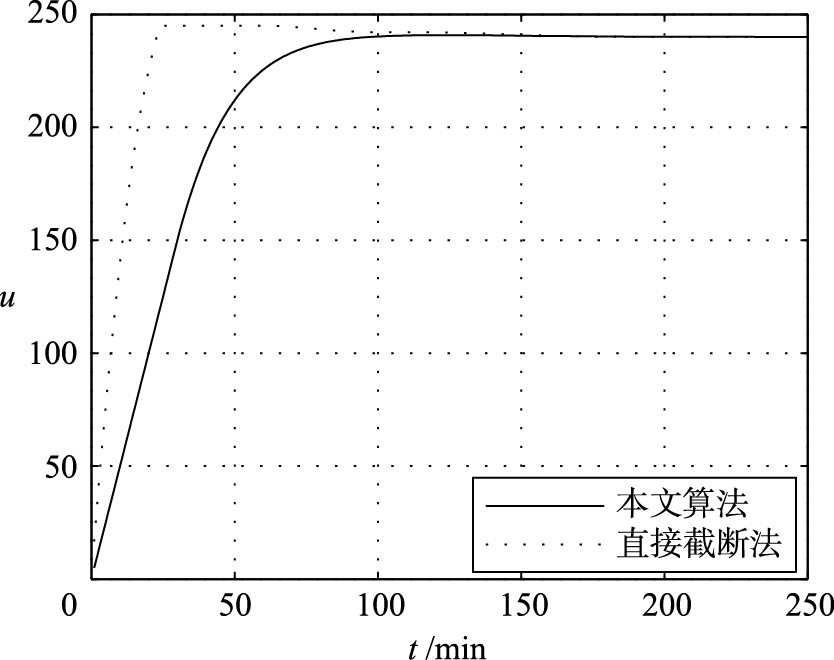 |
| 图 3 控制输入变化曲线 Fig. 3 The change curves of control input |
对比分析本文算法和采用直接截断法的仿真结果可知,在保证解析塔塔底温度输出量的前提下,通过二次插值法可以有效地把输入量控制在约束范围之内. 这是由于本文算法在处理约束条件时,自觉考虑了控制量的变化趋势,在工艺限定的区间内对约束进行了优化计算,得到优化的控制量可以使蒸气量大为降低,实现了节能减耗. 而直接截断法是直接把不满足约束要求的控制量采取截断的方式,在动态过程的前期阶段控制量的上升速率比较大,蒸气流量随之发生急剧变化,会对控制阀门造成损坏; 在动态过程中,直接截断法的控制量始终大于本文算法的控制量,所以也会造成能源的浪费. 因此,采用二次插值法不仅能在线优化处理解析塔的约束问题,也能起到一定的节能作用.
4.2 工控条件发生改变时仿真结果在系统工控情况发生改变时,在150 s时塔底温度设定值由原来的120 ℃变成80 ℃,进行MATLAB仿真. 塔底温度在工况改变后基于截断式的阶梯式DMC和本文方法的仿真结果比较如图 4、 5所示.
 |
| 图 4 工况改变时塔底温度输出响应曲线 Fig. 4 The output response curves of tower bottom temperature as working condition change |
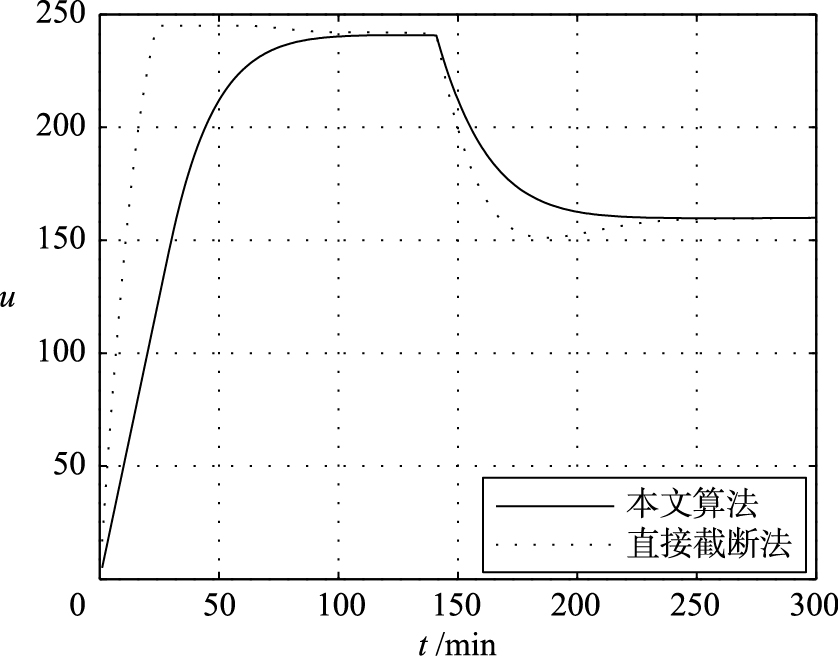 |
| 图 5 工况变化时控制输入变化曲线 Fig. 5 The change curves of control input as working condition change |
工况改变后,在图 4、 5仿真中可以看出,基于二次插值法的阶梯式DMC算法与直接截断方法相比,可以更快地回到期望值,调节时间变短. 而且在工况改变过程中,波动明显小于直接截断式,保证了生产过程的平稳过渡,提高了硫化氢与胺液分离时的纯度.
通过MATLAB的仿真验证可以看出,本文提出的算法应对工况改变时,相比截断式能更快地回到设定值.
4.3 抗干扰效果对比系统稳定的情况下,在t =140 s时施加一个阶跃干扰,输出如图 6、 7所示. 二者控制效果稳定且时间相近,在抗干扰性方面具有相近的控制效果.
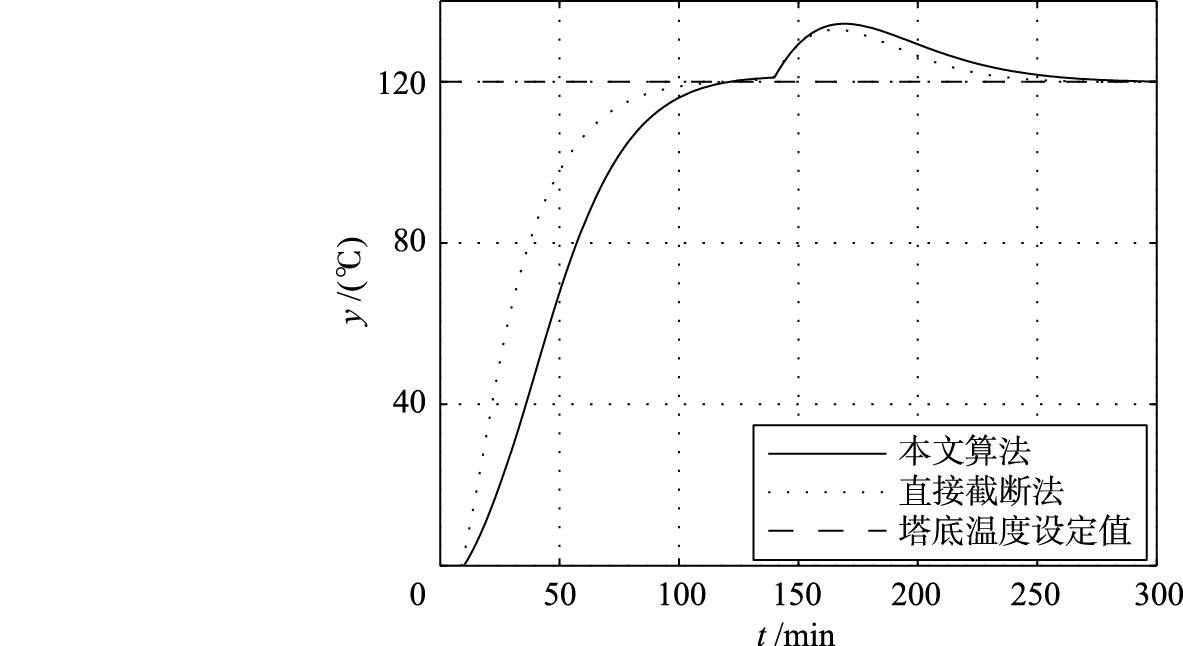 |
| 图 6 受干扰时塔底温度输出响应曲线 Fig. 6 The output response curves of tower bottom temperature as disturbed |
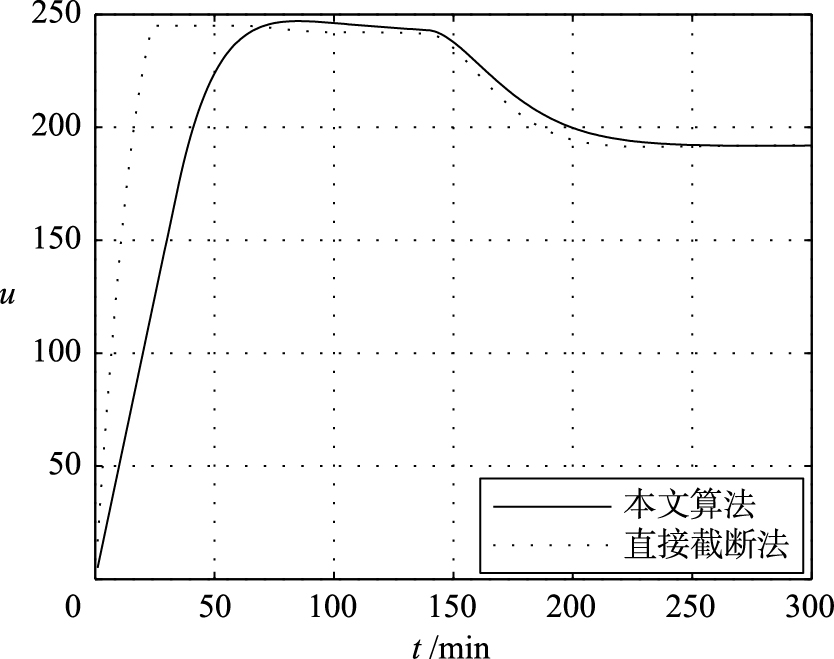 |
| 图 7 受干扰时控制输入变化曲线 Fig. 7 The change curves of control input as disturbed |
本文设计一种基于二次插值法的约束预测控制算法,处理解析塔工业控制中存在的输入输出约束问题. 该算法结合阶梯式动态矩阵控制把复杂的矩阵运算转换成标量运算,通过引进二次插值法处理约束问题,实现了系统在满足约束条件下塔底温度的平稳控制和控制输入的平缓变化. 而且,对比截断式方法,该算法在动态过程中显著降低了控制量,具有一定的节能减耗的作用. 但生产环境下带有不确定性问题的约束预测控制有待进一步研究.
| [1] | 席裕庚, 李德伟, 林姝. 模型预测控制——现状与挑战[J]. 自动化学报, 2013, 39(3):222-236. Xi Y G, Li D W, Lin M. Model predictive control-status and challenges[J]. Acta Automatica Sinica, 2013, 39(3):222-236. |
| [2] | Garcia C E, Prett D M, Morari M. Model predictive control:Theory and practice-A survey[J]. Automatic, 1989, 25(3):335-348. |
| [3] | Gao Y, Brennan J, Joseph P F, et al. A modal of the correlation function of leak noise in buried plastic pipes[J]. Journal of Sound and Vibration, 2004, 277(1/2):133-148. |
| [4] | 李少远. 工业过程系统的预测控制[J]. 控制工程, 2010, 17(4):407-415. Li S Y. Model-based predictive control for industrial process:A survey[J]. Control Engineering of China, 2010, 17(4):407-415. |
| [5] | Mayne D Q, Rawlings J B, Rao C V, et al. Constrained model predictive control:Stability and optimality[J]. Automatica, 2000, 36(6):789-814. |
| [6] | 李玉红, 刘红军, 王东风, 等. 简化的DMC-PID串级控制及其在汽温系统中的应用[J]. 电力科学与工程, 2003(4):62-64. Li Y H, Liu H J, Wang D F, et al. A simplified DMC-PID cascade control and its application in steam temperature system[J]. Electric Power Science and Engineering, 2003(4):62-64. |
| [7] | 邵克勇, 胡仲瑞, 王树峰, 等. 双曲线输入约束下一类基于斐波那契序列的变步长预测控制算法[J]. 化工自动化及仪表, 2013, 40(3):288-292. Shao K Y, Hu Z R, Wang S F, et al. Variable step size predictive control algorithm based on fibonacci sequence with hyperbolae input constraints[J]. Control and Instruments in Chemical Industry, 2013, 40(3):288-292. |
| [8] | 王国良, 阎威武, 陈世和, 等. 1000MW超超临界机组的多变约束预测控制的研究[J]. 控制理论与应用, 2012, 29(12):1573-1578. Wang G L, Yan W W, Chen S H, et al. Multivariable constrained predictive control of 1000 MV ultra supercritical once-trough boiler-turbine system[J]. Control Theory and Applications, 2012, 29(12):1573-1578. |
| [9] | 李国勇. 受约束动态矩阵控制算法的仿真研究[J]. 太原理工大学学报, 2004, 35(1):19-22. Li G Y. A constrained dynamic matrix control algorithm simulation[J]. Journal of Tai Yuan University of Technology, 2004, 35(1):19-22. |
| [10] | Camacho E F. Constrained generalized predictive control[J]. IEEE Transactions on Automatic Control. 1993, 38(2), 327-332. |
| [11] | 刘有飞, 吴刚, 魏衡华, 等. 阶梯式动态矩阵控制及在温度控制系统中的应用[J]. 中国科学技术大学学报. 2002, 32(3):347-352. Liu Y F, Wu G, Wei H H, et al. Step dynamic matrix control and its application in temperature control system[J]. Journal of University of Science and Technology of China, 2002, 32(3):347-352. |
| [12] | 刘云, 应康, 辛焕海, 等. 基于二次插值法的光伏发电系统控制策略[J]. 电力系统自动化, 2012, 36(21):29-35. Liu Y, Ying K, Xin H H, et al. Photovoltaic power generation system based on quadratic interpolation control strategy[J]. Automation of Electric Power Systems, 2012, 36(21):29-35. |
| [13] | 姚健. 群搜索算法与二次插值法的混合算法及其应用研究[D]. 太原:太原科技大学, 2010. Yao J. Group of hybrid search algorithm with quadratic interpolation algorithm and its application research[D]. Taiyuan:Taiyuan University of Science & Technology, 2010. |
| [14] | 邓建中. 加速迭代收敛的二次插值法[J]. 工程数学学报, 1998, 15(1):117-120. Deng J Z. Quadratic interpolation method to accelerate the convergence of iterative[J]. Journal of Engineering Mathematics, 1998, 15(1):117-120. |
| [15] | 席裕庚. 预测控制[M]. 北京:国防工业出版社, 1993. Xi Y G. Predictive control[M]. Beijing:National Defence Industry Press, 1993. |
| [16] | 舒迪前. 预测控制系统及其应用[M]. 北京:机械工业出版社, 1998. Su D Q. Predictive control system and its application[M]. Beijing:Mechanical Industry Publishing House, 1998. |
| [17] | 朱丰, 柏又青, 冯有前. 一种针对收敛性问题的改进进退法及其仿真验证[J]. 空军工程大学学报自然科学版, 2010, 11(2):86-90. Zhu F, BaiY Q, Feng Y Q. A kind of improvement for convergence problems in a method and its simulation[J]. Journal of Air Force Engineering University Natural Science Edition, 2010, 11(2):86-90. |
| [18] | 齐臣坤, 李少远. 基于阶跃响应测试的过程控制系统辨识与应用[D]. 上海:上海交通大学, 2004. Qi C K, Li S Y. Identification of the process control system based on step response test and application[D]. Shanghai:Shanghai Jiaotong University, 2004. |
| [19] | 梅华. 基于闭环阶跃测试的工业多变量过程分散辨识与自整定PID控制[D]. 上海:上海交通大学, 2006. Mei H. Based on the closed loop step test industrial decentralized multivariable process identification and self-tuning PID control[D]. Shanghai:Shanghai Jiaotong University, 2006. |
| [20] | 靳其兵, 蒋文春, 龙萍. 多变量时滞系统的闭环渐进辨识研究与应用[J]. 化工自动化及仪表, 2009, 36(5):74-78. Jin Q B, Jiang W C, Long P. Closed-loop multivariable systems with time delay gradual recognition research and application[J]. Journal of Chemical Industry Automation and Instrument, 2009, 36(5):74-78. |



