1 引言
电力负荷的准确、快速预测不仅有利于提高电力系统运行的经济性和可靠性，也是电力系统进行科学调度和管理的重要依据之一. 目前短期电力负荷的预测方法主要有回归分析法、模糊逻辑推理法、小波分析法、神经网络及混沌模型法等[1, 2, 3, 4, 5]. 其中，人工神经网络因其具有强大的非线性映射能力，在电力负荷领域得到了广泛应用[6, 7, 8]. 但是由于神经网络训练是基于经验风险最小化原则，故易产生过学习从而导致泛化能力下降，另外还存在诸如网络结构难以确定、易陷入局部极小和过分依赖大样本学习等缺陷. 支持向量机(support vector machines，SVM)是Vapnik等[9, 10]在统计学习理论基础上提出的一种新的机器学习方法. 由于SVM基于结构风险最小化思想，克服了神经网络学习中存在“过学习”和“维数灾难”等固有缺陷. 因此，在处理高维数、小样本和非线性问题方面体现出了独特的优势，具有很强的泛化能力，目前已成为电力负荷预测领域的研究热点 [11, 12].
尽管标准SVM具有良好的非线性性能和泛化能力，但其训练过程涉及到求解有约束二次规划问题，这将导致训练时消耗大量时间，直接影响模型的预测精度. 作为SVM的扩展，最小二乘支持向量机(least squares support vector machines，LS-SVM)将SVM中二次规划问题转化为线性方程组求解问题，大大提高了学习速度，而且算法简练[13]. 文[14]基于LS-SVM算法建立了电力负荷预测模型，仿真结果表明该模型具有良好的预测性能. 但LS-SVM算法在解决SVM计算复杂的同时，也产生了模型鲁棒性能下降的问题. Suykens等[15]在LS-SVM算法中引入加权规则，提出加权最小二乘支持向量机(weighted least squares support vector machines，WLS-SVM)算法. WLS-SVM算法采用依据样本训练的重要性分别赋予其不同权重的方法，从而改善标准LS-SVM鲁棒性能欠佳的问题. 文[16]基于该算法建立了电力负荷预测模型.
由于受到人为因素或突发事件以及某些特殊工况的影响，电力负荷数据常常含有异常值，直接影响电力负荷预测模型的精度和可靠性. 因此，本文提出一种基于自适应加权最小二乘支持向量机(adaptive weighted least squares support vector machines，AWLS-SVM)的短期电力负荷预测算法. 该算法继承了LS-SVM快速学习的优点，并利用改进的正态分布加权规则自适应地为每个建模样本分配不同的权值，以消除异常样本点对模型性能的影响，提高模型的鲁棒性能. 考虑到LS-SVM中正则化参数和核宽度参数对模型预测精度和泛化能力有较大的影响，故采用一种具有动态惯性权重和随机杂交相结合的粒子群优化遗传算法(particle swarm optimization genetic algorithm，PSO-GA)对参数进行优化选择，以减少参数选择的盲目性，最后以北方地区某城市电力负荷为例检验AWLS-SVM算法在短期电力负荷预测中的有效性.
2 自适应加权最小二乘支持向量机 2.1 最小二乘支持向量机支持向量机是以统计学习理论为基础而发展起来的一种机器学习方法，最小二乘支持向量机则是把标准支持向量机中的误差ξi的二范数定义为损失函数，并将不等式约束改为等式约束，从而有效提高模型的训练速度. 假定训练样本集合为｛(xi， yi)|i=1，2，…，N｝，其中， xi∈Rd为d维输入样本，yi∈R为输出样本，则优化问题可描述为[13, 17]
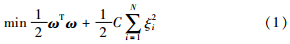
式中，ω是权系数向量，φ(·)是输入空间到高维空间的映射，C是正则化参数，b是阈值，ξi是拟合误差. 通过引入拉格朗日函数：
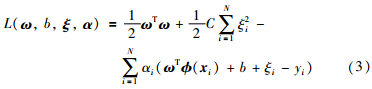
式中，αi(i=1，2，…，N)为拉格朗日乘子，根据优化条件引入核函数：
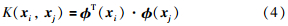
则式(3)的优化问题可变为以下线性方程组的求解问题：
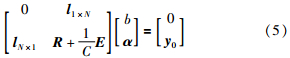
式中，l1×N是1×N的单位行向量，lN×1是N×1的单位列向量，E是N×N单位阵，
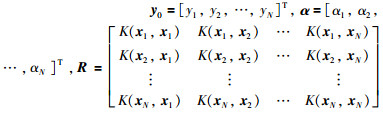
这样就可以得到回归函数的形式如下：
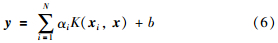
LS-SVM算法在解决了SVM计算复杂的同时，也产生了算法鲁棒性能下降的问题. Suykens等在LS-SVM算法的基础上提出加权最小二乘支持向量机(WLS-SVM)算法，改善了LS-SVM算法鲁棒性能欠佳的问题. 现对式(1)中误差的2范数ξ2i进行加权处理，设ξ2i的权值为vi，则对应的优化问题可以描述为
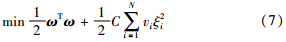
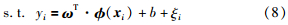
引入拉格朗日函数：
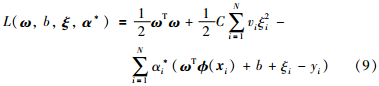
式中，αi*(i=1，2，…，N)为拉格朗日乘子，根据优化条件，同样引入核函数如式(4)，则式(9)的优化问题变为以下线性方程组的求解问题：
式中，对角阵V=diag(v1-1，v2-1，…，vN-1)，α*=[α1*，α2*，…，αN*]T，其它的参数同前，如此可得回归函数的形式如下：
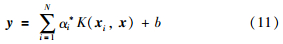
显然，与LS-SVM相比，WLS-SVM在建模过程中考虑了样本数据对回归模型的影响，并根据模型拟合误差的大小，赋予建模样本不同的权重，使得权值能够决定每个样本点对建模过程贡献的大小，以提高模型的抗干扰能力和鲁棒性能. 具有代表性的加权因子确定方法是由Suykens等[15]提出，权值表达式如下：
式中，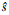
是LS-SVM样本误差ξi的标准方差的鲁棒估计：
IQR是样本误差ξi的四分位差； s1和s2根据样本误差大小分布来决定.
由于式(12)所确定的权值是线性分布的，因此对样本的取舍存在一定的错误判断，文[18]在式(12)基础上提出了新的权值表达式：
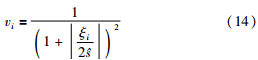
以上两种加权方法的本质都是根据建模样本的预测误差来进行加权. 如果误差大，则表明该样本对模型的贡献小，相应的权值则小，反之亦然. 然而在对具有强非线性的过程系统进行建模过程中，建模数据对过程模态的描述往往不是很充分，信息重复出现在几个工作点附近，用于建模的样本具有冗余的特性. 此外由于样本所包含的“异常点”和“拐点”的量不多，模型对于这些特殊点的表达不明显，数据模型易出现过度拟合. 如果按照上述两种方法进行加权，模型对这些特殊点的表达反而更加恶化.
为了兼顾异常点对数据模型的贡献及削弱冗余数据造成模型的“过度拟合”，根据具有全局特性的正态分布概率密度函数的特性，本文提出基于改进正态分布的加权方法，权值表达如下：
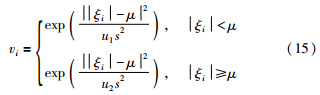
式中，μ为误差绝对值丨ξi丨的平均值：
u1和u2为宽度调整参数，s为误差绝对值丨ξi丨的标准差：
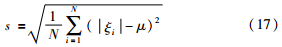
采用正态分布的权值表达式，拟合误差处于中间的样本所赋予的权值较大，而拟合误差很小或很大时，相应的权值则很小. 因此基于正态分布加权方法更注重训练样本的实际特性，同时也能削弱异常点对模型的影响. 然而，标准正态曲线在调整参数过程中，其对称轴两侧分布曲线总是同时发生变化，无法合理区分样本有效特征点和异常点对模型影响的程度. 因此，本文通过设置式(15)中宽度调整参数u1和u2，使加权因子对支持向量具有调优的功能. 其权值分布图形如图 1所示.
 |
| 图 1 改进的WLS-SVM权值分布 Fig. 1 Distributing chart of improved WLS-SVM weights |
图 1中虚线为正态分布的曲线，实线为式(15)所表示的曲线，与正态分布加权规则相比，本文提出的改进正态分布加权规则能够实现权值在对称轴两侧自由调整，使得权值分配机制更加合理，从而有效处理建模过程中异常点和过拟合问题对模型的影响.
综上所述，本文提出的自适应加权最小二乘支持向量机算法步骤如下：
1) 选取训练样本数据，根据式(5)求解b、α，建立LS-SVM模型，再根据模型重新计算各个样本的拟合误差ξi；
2) 计算权值. 根据LS-SVM模型拟合误差ξi，按式(15)计算各个样本的权值vi；
3) 根据各个样本的权值vi，由式(10)求解b、α*，建立WLS-SVM模型，并再次计算各个样本的拟合误差ξi；
4) 利用得到的拟合误差ξi，根据式(15)重新计算各个样本的权值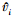
；
5) 定义权值平均变化量Ve：
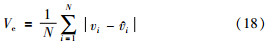
如果权值已经收敛，即满足Ve<Vemin，则迭代终止，并把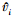定为AWLS-SVM模型的权值； 否则，更新各个样本的权值vi，并返回步骤3)；
6) 按最终得到的权值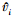建立AWLS-SVM模型.
高斯径向基函数具有良好的处理样本输入与输出之间复杂非线性关系的能力，而且需要确定的参数少，计算效率高，因此本文定义LS-SVM的核函数为高斯径向基函数：
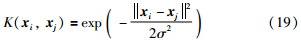
式中，σ为核宽度参数.
相关研究表明，最小二乘支持向量机的正则化参数C及核宽度参数σ对模型的预测精度及泛化能力都有比较大的影响[19]. 文献中关于参数的选择大多依靠试算和经验的方法进行确定，这不仅计算耗时且结果不够准确. 采用群智能优化算法对参数进行优化选择不仅可以缩短时间，也降低了对初值选取的依赖性.
PSO是一种通用的启发式搜索技术，该算法虽具有简单易行、优化效率高和鲁棒性好等优势，但其易陷入局部最优解. 为了提高标准PSO算法的全局寻优能力，文[20]提出一种具有动态惯性权重和随机杂交相结合的粒子群遗传优化算法，该算法充分利用遗传算法中交叉变异和种群移动均匀特性，从而有效克服PSO局部最优和早熟收敛的缺陷. 因此，具有良好的寻优速度和计算精度. 采用该算法对LS-SVM的正则化参数C和核宽参数σ进行优化选择，优化关键步骤如下：
1) 建立待优化目标函数：
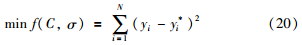
式中，yi为第i个样本实际值，yi*为第i个样本预测值. 设定约束集C∈(Cmin，Cmax)和σ∈(σmin，σmax)；
2) 初始化种群中各粒子的位置和速度，将参数(C，σ)的值表示为粒子的位置；
3) 计算粒子适应度值，以更新粒子位置和速度；
4) 根据杂交概率选取指定数量的粒子随机杂交产生子代粒子；
5) 评价粒子种群是否满足最优解条件，如果满足则输出最优参数(Cbest，σbest)，否则返回步骤3)再次计算粒子适应度.
在式(15)中，u1、u2用于调节权值分布范围，其值的选择是否合适对模型的预测精度亦有较大的影响，这里同样使用粒子群遗传算法优化参数u1和u2的值.
3 数值仿真实验为了验证上述算法的有效性，本文选择1维函数作为数值仿真测试：
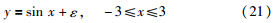
式中，ε是服从正态分布N(0，0.06)的噪声. 现在输入变量域内随机产生76组数据，选择其中的41组作为训练样本，余下的35组作为测试样本. 在训练样本数据中，对第10、12、30和32个样本加入1.3倍的扰动，这些数据可以视为异常点.
基于41个训练样本，分别采用AWLS-SVM、WLS-SVM和LS-SVM建立模型，进而对35个测试样本进行预测，结果如图 2和图 3所示.
 |
| 图 2 3种建模方法训练结果比较 Fig. 2 Comparison of training results among three modeling methods |
 |
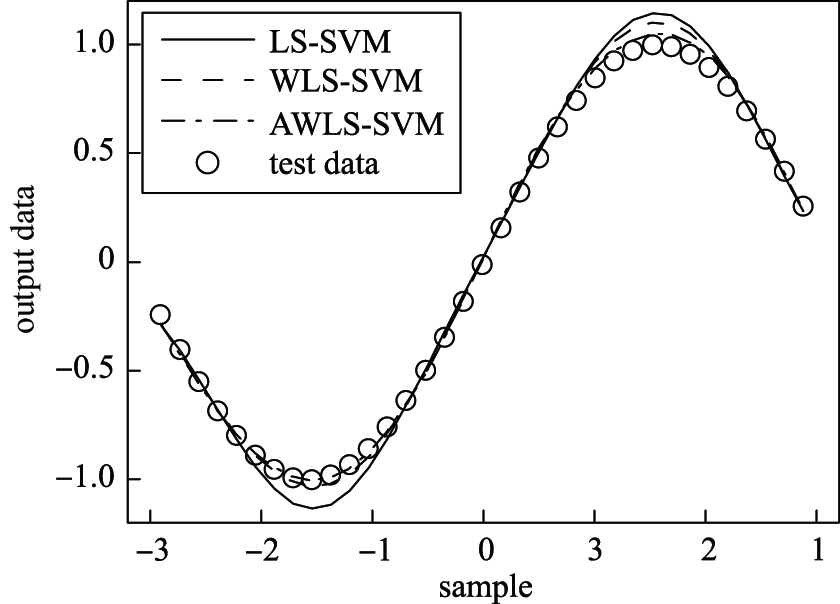| 图 3 3种建模方法测试结果比较 Fig. 3 Comparison of testing results among three modeling methods |
从图 2和图 3的拟合结果及预测结果可以看出，AWLS-SVM和WLS-SVM算法对每个样本进行了加权处理，都能有效消除异常样本点的影响，具有较好的鲁棒性及预测精度； 但WLS-SVM的权值没有进一步调整，所以其预测效果不如AWLS-SVM算法. 而LS-SVM未进行加权处理，使得模型受到异常样本点的影响比较严重而偏离真实值，从而降低了模型的预测精度.
图 4所示为基于AWLS-SVM和WLS-SVM模型的各个训练样本点的权值. 从中可以看出，基于AWLS-SVM和WLS-SVM模型的正常样本点的权值都在0.8以上，而4个异常样本点的权值均小于0.8，可知4个异常点和正常样本点的权值具有明显差距，从而有效降低了异常样本点对模型性能的影响； 同时，基于WLS-SVM模型的4个异常样本点的权值在0.7左右，而基于AWLS-SVM模型的4个异常样本点的权值均不超过0.4. 这说明，相比于WLS-SVM模型，AWLS-SVM模型通过权值自适应调整，将异常样本点区分得更加明显，进而降低异常点对建模过程的影响，提高模型的可靠性及预测精度.
 |
| 图 4 训练样本权值 Fig. 4 Weights of training sample |
为了进一步比较模型的性能，采用最大误差(MaxEr)、平均绝对误差(MAE)和均方根误差(RMSE)作为评价指标来对模型的预测性能进行评价，3种指标定义分别为
式中，N为样本数量，yi为实际值，yi*为预测值.
表 1给出了基于41个含异常点的训练样本数据，分别采用AWLS-SVM、WLS-SVM和LS-SVM建立的模型，对35个测试样本数据预测的最大误差(MaxEr)、平均绝对误差(MAE)和均方根误差(RMSE)的比较结果. 从表 1可以看出采用AWLS-SVM模型预测的结果优于另外两种模型.
| Models | C | σ | MaxEr | MAE | RMSE |
| LS-SVM | 502.1 | 0.35 | 0.146 | 0.061 7 | 0.078 1 |
| WLS-SVM | 502.1 | 0.35 | 0.103 | 0.038 4 | 0.048 9 |
| AWLS-SVM | 502.1 | 0.35 | 0.052 | 0.025 8 | 0.031 4 |
电力系统负荷预测是指在充分考虑一些重要的系统运行特征、增容决策、自然条件与社会影响的条件下，利用一套系统处理过去与未来负荷的数学方法，在满足一定精度要求的意义下，确定未来某特定时刻的负荷数值[21].
4.1 建模步骤由于人为因素或突发事件及某些特殊原因的存在，采样得到的负荷数据常常含有异常值，将影响预测结果的精度及可靠性. 为了降低负荷数据异常值对模型性能的影响，提高预测精度，采用本文第2节所讨论的AWLS-SVM的建模方法，建立短期电力负荷预测模型，建模关键步骤如下：
1) 构造样本集. 短期电力负荷有着明显的时段波动特性，而且还与气象参数(温度)有一定的关系，这里选择时段属性x1、星期属性x2、温度x3和前一时刻负荷值x4所构成的特征向量作为训练样本集.
电力负荷数据为每隔0.5 h采样一次的值，所以定义时段属性：
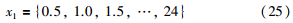
用于对应时刻值00∶30，01∶00，01∶30，…，24∶00； 定义星期属性：
用于对应一个星期中的周一，周二，…，周日；
2) 数据归一化处理. 为了避免计算出现饱和现象，并充分发挥模型的预测功能，提高其预测精度，需要对样本数据进行归一化处理：
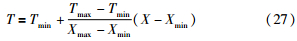
式中，X是原样本数据，Xmax和Xmin分别代表样本数据中最大值和最小值，T是目标数据，Tmax是目标数据的最大值，取Tmax=7，Tmin是目标数据的最小值，取Tmin=0.1. 这里按式(27)对样本数据进行归一化.
3) 按2.2.2小节步骤1)～6)建立AWLS-SVM模型，输入新的样本数据可得到模型输出；
4) 反归一化. 按式(28)对模型输出进行反归一化处理：
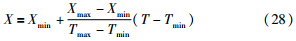
可得到电力负荷对应的预测值.
4.2 实例分析本文选取北方地区某城市电网夏季、冬季的部分数据作为验证AWLS-SVM模型方法的数据. 其中，夏季的训练样本选择2007年6月4日15∶00～11日14∶30每隔0.5 h的负荷数据和相应的气象数据，测试样本为11日15∶00～12日14∶30每隔0.5 h的负荷数据； 冬季的训练样本选择同年度12月3日15∶00～10日14∶30每隔0.5 h的负荷数据及相应的气象数据，测试样本为10日15∶00～11日14∶30的负荷数据.
以夏季的训练样本数据建立基于AWLS-SVM的短期电力负荷预测模型，对测试样本数据进行预测. 为比较该方法建模的预测效果，同时也建立WLS-SVM模型及LS-SVM模型，图 5为这3种模型的训练结果； 图 6中为这3种模型的预测结果对比.
 |
| 图 5 3种模型方法的训练结果 Fig. 5 Training results of three modeling methods |
 |
| 图 6 3种模型方法的预测结果 Fig. 6 Predictive results of three modeling methods |
从图 6可知，AWLS-SVM模型具有较强的抗干扰能力及较高的预测精度，经过对误差平方的权值自适应调整，进一步减小了预测数据的误差，其预测误差均小于WLS-SVM模型和LS-SVM模型. 总体预测性能优于WLS-SVM模型及LS-SVM模型.
按式(22)～式(24)所示的3种评价指标： 最大误差(MaxEr)、平均绝对误差(MAE)和均方根误差(RMSE)对以上3种模型进行比较，结果如表 2所示.
| Models | C | σ | MaxEr | MAE | RMSE |
| LS-SVM | 3 249.1 | 6.2 | 37.816 | 8.721 | 12.361 |
| WLS-SVM | 3 249.1 | 6.2 | 36.686 | 8.512 | 12.100 |
| AWLS-SVM | 3 249.1 | 6.2 | 36.255 | 8.214 | 11.632 |
由表 2可知，AWLS-SVM模型预测的平均绝对误差为8.214，较WLS-SVM模型的8.512及LS-SVM模型的8.721都要小. 另外，通过计算对比，AWLS-SVM模型预测的均方根误差比LS-SVM模型降低了5.90％，比WLS-SVM模型降低了3.87%. 可见，AWLS-SVM模型方法在短期电力负荷预测方面较WLS-SVM模型及LS-SVM模型有更高的预测精度.
以冬季的训练样本分别建立AWLS-SVM、WLS-SVM及LS-SVM的短期电力负荷预测模型，并用于测试样本的预测，其预测输出对比如图 7所示.
 |
| 图 7 3种模型方法的预测结果 Fig. 7 Predicting results of three modeling methods |
由图 7可知，将AWLS-SVM模型方法应用于冬季的短时电力负荷预测，能很好地跟踪负荷变化，保持良好的预测效果. AWLS-SVM方法通过赋予每个样本数据合适的权值，减小了预测数据的误差，使得模型具有较高的预测精度及鲁棒性能.
5 结论本文提出一种基于自适应加权最小二乘支持向量机的短期电力负荷预测算法，通过自适应加权规则赋予每个样本不同的权重值，降低了异常训练样本点对模型性能的影响，并采用粒子群遗传算法对模型重要参数进行优化选择，进一步提高模型的预测精度. 数值仿真实验表明，当使用含噪声样本训练模型时，AWLS-SVM模型预测效果优于WLS-SVM模型和LS-SVM模型.
使用北方地区某城市电网的负荷数据作为样本数据，建立基于AWLS-SVM短期电力负荷预测模型，并进一步对该模型和WLS-SVM及LS-SVM模型的预测性能进行比较. 结果表明AWLS-SVM模型具有较高的预测精度、抗干扰能力及泛化能力. 因此，AWLS-SVM算法在短期电力负荷预测中是有效的.
| [1] | Zhang K, Wang Y H. Short-term load forecasting for electric power system based on DB wavelet and regression BP neural networks[J]. Applied Mechanics and Materials, 2013, 380/381/382/383/384:3018-3021. |
| [2] | Bashir Z A, El-Hawary M E. Applying wavelets to short-term load forecasting using PSO-based neural networks[J]. IEEE Transactions on Power Systems, 2009, 24(1):20-27. |
| [3] | Nose-Filho K, Lotufo A D P, Minussi C R. Short-term multinodal load forecasting using a modified general regression neural network[J]. IEEE Transactions on Power Delivery, 2011, 26(4):2862-2869. |
| [4] | Kavousi-Fard A. A new fuzzy-based feature selection and hybrid TLA-ANN modelling for short-term load forecasting[J]. Journal of Experimental & Theoretical Artificial Intelligence, 2013, 25(4):543-557. |
| [5] | Zhao Y H, Zhao X C, Cheng W. The application of chaotic particle swarm optimization algorithm in power system load forecasting[J]. Advanced Materials Research, 2013, 614/615:866-869. |
| [6] | Adepoju G A, Ogunjuyigbe S O A, Alawode K O. Application of neural network to load forecasting in nigerian electrical power system[J]. The Pacific Journal of Science and Technology, 2007, 8(1):68-72. |
| [7] | Yalcinoz T, Eminoglu U. Short term and medium term power distribution load forecasting by neural networks[J]. Energy Conversion and Management, 2005, 46(9/10):1393-1405. |
| [8] | Guan C, Luh P B, Michel L D, et al. Very short-term load forecasting:Wavelet neural networks with data pre-filtering[J]. IEEE Transactions on Power Systems, 2013, 28(1):30-41. |
| [9] | Vapnik V. The nature of statistical learning theory[M]. Berlin, Germany:Springer, 1999. |
| [10] | Cortes C, Vapnik V. Support-vector networks[J]. Machine Learning, 1995, 20(3):273-297. |
| [11] | Wang J M, Ren G Q. A improved SVM and its using in electric power system load forecasting[C]//Proceedings of the 13th International Conference on Neural Information Processing. Berlin, Germany:Springer, 2006:847-855. |
| [12] | Niu D X, Wang Y L, Duan C M, et al. A new short-term power load forecasting model based on chaotic time series and SVM[J]. Journal of Universal Computer Science, 2009, 15(13):2726-2745. |
| [13] | Suykens J A K, Vandewalle J. Least squares support vector machines classifiers[J]. Neural Processing Letters, 1999, 9(3):293-300. |
| [14] | Liu B Y, Yang R G. Short-term load forecasting model based on LS-SVM with PCA[J]. Electric Power Automation Equipment, 2008, 28(11):13-17. |
| [15] | Suykens J A K, de Brabanter J, Lukas L, et al. Weighted least squares support vector machines:Robustness and sparse approximation[J]. Neurocomputing, 2002, 48(1/2/3/4):85-105. |
| [16] | 王晓红, 吴德会. 基于WLS-SVM回归模型的电力负荷预测[J]. 微计算机信息, 2008, 24(4):312-314. Wang X H, Wu D H. Power load forecasting based on the WLS-SVM regression model[J]. Microcomputer Information, 2008, 24(4):312-314. |
| [17] | Ding L Z, Liao S Z. Approximate model selection for large scale LSSVM[J]. Journal of Machine Learning Research-Proceedings Track, 2011(20):165-180. |
| [18] | 陶莉莉, 钟伟民, 罗娜, 等. 基于粗差判别的参数优化自适应加权最小二乘支持向量机在PX氧化过程参数估计中的应用[J]. 化工学报, 2012, 63(12):3943-3950. Tao L L, Zhong W M, Luo N, et al. Adaptive weighted least square support vector machine regression with gross error detection and its application to estimate kinetic parameters for industrial oxidation of p-xylene[J]. CIESC Journal, 2012, 63(12):3943-3950. |
| [19] | 樊晓雪. 最小二乘支持向量机的参数选择[D]. 保定:河北大学, 2012. Fan X X. Least squares support vector machine parameter selection[D]. Baoding:Hebei University, 2012. |
| [20] | 韩富春, 刘利红, 岳永新. 基于改进粒子群算法的电力系统无功优化研究[J]. 电气技术, 2011(7):6-13. Han F C, Liu L H, Yue Y X. Research of particle improved swarm algorithm in power system reactive power optimization[J]. Electrical Engineering, 2011(7):6-13. |
| [21] | 冉启文, 单永正, 王骐, 等. 电力系统短期负荷预报的小波-神经网络-PARIMA方法[J]. 中国电机工程学报, 2003, 23(3):38-42. Ran Q W, Shan Y Z, Wang Q, et al. Wavelet-neural networks-PARIMA method for power system short term load forecasting[J]. Proceedings of the CSEE, 2003, 23(3):38-42. |