2. 哈尔滨工业大学计算机科学与技术学院, 黑龙江 哈尔滨 150001
2. School of Computer Science and Technology, Harbin Institute of Technology, Harbin 150001, China
1 引言
自从Shapiro在EZW(embedded zero-tree wavelet)算法中提出零树编码思想,尤其是ISO JPEG2000标准的建立,使得小波图像编码当之无愧地成为图像压缩技术的主流. 而随着多尺度几何分析(multiscale geometric analysis,MGA)概念的提出,将小波与MGA结合形成新的编码方案吸引了很多研究人员的注意力[1, 2]. 其中,Do和Vetterli提出的Contourlet变换[3]是一种多分辨率、 多方向的几何分析方法,能够很好地刻画高维信息特性. 但由于该变换中采用了LP(Laplacian pyramid)变换,在处理高频信息时没有进行下采样操作,导致Contourlet较Mallat塔式分解存在1/3冗余. 为此,Eslami和Radha提出基于小波的Contourlet变换(wavelet-based Contourlet transform,WBCT)[4],用小波变换中的Mallat塔式分解代替Contourlet中的LP分解,去除了LP滤波器结构引入的数据冗余,形成了非冗余且完全重构的滤波器组,能够有效地逼近图像,更适合于图像压缩.
作为WBCT的提出者,Eslami和Radha采用改进的SPIHT(set partitioning in hierarchical trees)算法结合零树对包含较多纹理和轮廓的图像进行编码[4],其重构图像的PSNR值与SPIHT算法相近,但在视觉效果上明显好于后者. 考虑到WBCT系数父子关系与小波系数的不同,Eslami和Radha又提出了一种WBCT系数定位算法[5],使得压缩算法(CSPIHT)可以采用与原始SPIHT算法类似的方向树结构,从而提高了富含方向特征图像的压缩效率. 这两种算法奠定了基于小波的Contourlet变换编码的基础. 此后的研究人员围绕小波和Contourlet开展了更为广泛的研究工作. 王力[6]在对原始图像进行小波分解后,对中高频小波子带进一步实施Contourlet自适应方向分解,以构造扩展空间方向树结构,并根据系数重要性,对低频系数重新排列,最后采用SPIHT编码思想完成图像压缩. Hung[7]则提出一种短长度2-D滤波器进行方向变换,并且方向变换仅对选定的子带进行,而子带的选择由基于均值—平移的决策过程实现. Fan[8]在Contourlet变换过程中采用了分类隐马尔可夫树(classified hidden Markov tree,CHMT),并通过计算系数间的统计关系来优化编解码过程. Tamilarasi[9]采用C均值算法选择感兴趣区并进行Contourlet变换,而对非感兴趣区则采用小波变换,并采用改进的嵌入式零树小波算法实现编码. 白璘[10]对高光谱图像的每一个波段进行基于小波的Contourlet变换,然后用前一波段的变换系数预测当前波段,最后对预测误差进行SPIHT编码,形成嵌入式码流.
以上算法存在2个主要问题: (1) 从变换本身来看,Contourlet在进行方向滤波的时候,为避免能量流失,对最低频子带未进行分解; 而对高频子带,采取不同子带方向滤波分解数目固定的方式,没有充分考虑图像本身的特性. (2) 从编码方法上看,以上方法均采用树结构组织系数,对Contourlet变换的方向滤波分解有一定约束,否则将破坏有效树结构的形成,需要进行复杂的系数重排操作. 由于决定图像质量的关键因素往往体现在图像的纹理和边缘等细节特征上,而这些特征主要分布在图像的高频区域,为此本文引入熵[11]作为控制小波高频子带方向分解的依据,提出利用子带熵最小化原则实现Contourlet方向滤波分解的优化. 在此基础上将其与基于块的SPECK图像编码算法相结合,并根据视觉敏感度带通特性对不同子带进行加权处理. 实验结果表明,算法的峰值信噪比得到明显提高,而且对局部纹理的失真明显减小.
2 Contourlet方向滤波优化处理 2.1 Contourlet变换简介Contourlet变换主要包括2个过程: (1)对原始图像进行低通滤波,获得低频近似图像和高频细节部分; (2)对所获得的高频部分进行方向滤波,这种滤波方式各向异性且可以在任意方向上进行分解. 图 1给出了Contourlet变换对图像进行多尺度及方向分解的示意图.
 |
| 图 1 Contourlet变换Fig. 1 Contourlet transform |
Contourlet变换低通近似图像通过采用LP变换实现. Do和Vetterli用框架理论和过采样滤波器组研究了LP变换,证明用正交滤波器组实现的拉普拉斯金字塔变换是一个框架界为1的紧框架. 对于高频细节部分进行方向滤波分解,即将高频部分分解于各个频带方向上,每一层频域分解为2l个子带. 图 2给出了8方向的频域子带分解示意图.
 |
| 图 2 楔型频域子带分解Fig. 2 Wedge-shaped sub-band decomposition in frequency domain |
实现方向滤波的关键是使用良好的方向滤波器. 最大抽样条件下可完全重建的方向滤波器组(direction filter bank,DFB)由Bamberger和Smith提出[12],它对图像进行l级二叉树状结构分解,将频域划分为2l个锲形(wedge shape)子带. 但构造DFB时所采用的调制器和重采样矩阵会导致频谱平移和几何变换失真,严重影响了DFB的方向选择特性. 此外,使用菱形滤波器对输入信号进行调制,需要进行一个非常复杂的树结构扩展,所得的方向子带也需要重新进行排列. Do和Vetterli等[13]在继承DFB多方向分解理论的基础上,提出了使用扇形结构的共轭镜像DFB构造方法,避免了对输入信号的调制. 同时将l层二叉树状结构的方向滤波器构成2l个并行通道结构,表现出良好特性[14].
2.3 基于熵的Conturlet方向滤波优化基于以上对Conturlet变换特性的分析,子带的方向分解数目对图像重构质量有很关键的影响. 首先低频子带不进行方向分解,否则将会造成能量的流失,从而严重影响图像的重构质量. 高频子带的分解数目和其细节纹理/边缘信息有较大关系,需要尽可能符合其本身的特点. 根据文[15],描述高频子带纹理/边缘特征的一个重要指标是熵. 由于Contourlet根据方向信息将临近的奇异点连接成轮廓且使用一个系数表示,因此方向分解必然引起子带熵的变化且熵的大小与分解的方向数目有关. 根据熵的定义,如果方向分解后小波系数分布更加有规律(对编码有利),其熵值必定减小. 因此,最佳的方向分解数应使小波子带的熵达到最小值.
设s为经Contourlet方向分解后的任意一个子带,定义该方向子带的熵:

其中,p(i)为像素灰度值为i的概率,p(i)=ni/ns,ni为灰度值为i的像素数目,ns为子带s的像素总数.
当对小波子带进行不同数目的方向分解时,其熵值发生变化. 熵值变大,表明有“轮廓”被打散; 反之,熵值变小,则表明有系数被合并成为“轮廓”. 为此,对某一小波高频子带S,若其分解方向数目为2j(j=0,1,2,…),则其平均熵为

算法1 基于熵的Contourlet方向滤波分解优化算法步骤为:
(1) 对图像进行L级小波变换,得到3L个高频子带和1个低频子带.
(2) 选取某一待分解小波高频子带S,假定其为第i(1≤i≤L)级,确定其初始方向分解数为2j=2L-i+1.
(3) 若  ,则选取方向分解数为2j,转步骤(6); 否则,转步骤(4).
,则选取方向分解数为2j,转步骤(6); 否则,转步骤(4).
(4) 若j≤1,选取方向分解数为1,转步骤(6); 否则转步骤(5).
(5)令j=j-1,返回步骤(3).
(6) 如果所有小波高频子带处理完毕,则算法结束; 否则,返回步骤(2).
算法1流程如图 3所示.
 |
| 图 3 算法1流程图Fig. 3 The flow chart of the algorithm 1 |
人类视觉系统(human vision system,HVS)是现有最精细最复杂的图形图像处理系统. 很多实验结果证实,基于HVS的图形图像处理算法往往能在主观和客观两个方面都取得较好的结果[16].
HVS具有很多特性,诸如视觉非线性特性、 视觉敏感度带通特性、 视觉多通道及掩盖效应等. 其中,视觉敏感度带通特性模型由对比度敏感函数(contrast sensitivity function,CSF)表示. CSF能较全面、 客观地评价视觉功能. 一般情况下,不同实验所得的CSF函数形式并不相同,这取决于图像本身的属性. 但可以确定的是HVS的对比度是空间频率的函数且具有带通滤波器的性质,为各向异性. 目前常用的CSF函数表达式由Miloslavski和Ho给出[17],表示为
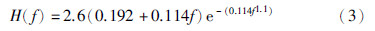
其中f为空间频率. CSF函数的频率响应曲线如图 4所示,它代表了人类视觉的带通特性. 可以看出,人类视觉对于低频部分对比度变化最为敏感,在高于一定频率成分后,视觉敏感度逐渐降低且具有明显的方向性.
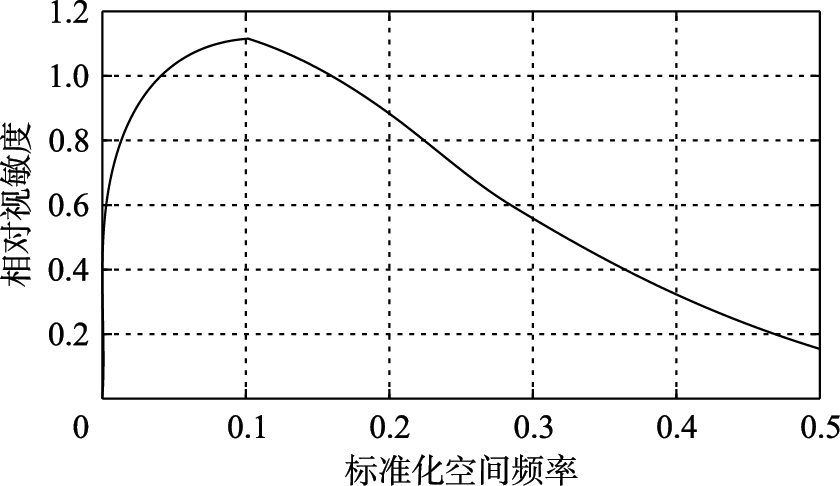 |
| 图 4 CSF频率响应曲线Fig. 4 Frequency response curve of CSF |
图像经过小波变换后所得到的子带与HVS十分吻合,在图像编码中利用HVS的掩盖效应,对不同子带内的小波系数赋予不同的视觉权值(human visual weight,HVW),保证优先传输视觉上的重要信息,可以进一步提高图像重构质量. 假定对图像进行5级小波分解,用类似于Kim的计算[18],可得16个子带的视觉加权,如表 1所示. 其中,根据CSF的频率特性,对中低频子带分配了较高的权重,对最高频子带的加权系数最低. 根据CSF的方向特性,在同一级分辨率中,分配给LH和HL子带的加权系数相同,而对角方向子带的权重相对较低.
| LH1 | HL1 | HH1 | LH2 | HL2 | HH2 | LH3 | HL3 |
| 0.362 | 0.362 | 0.082 | 0.843 | 0.843 | 0.516 | 0.981 | 0.981 |
| HH3 | LH4 | HL4 | HH4 | LH5 | HL5 | HH5 | LL5 |
| 0.938 | 0.962 | 0.962 | 0.849 | 0.798 | 0.798 | 0.684 | 1.00 |
由于WBCT采用小波变换中的Mallat塔式分解代替Contourlet变换中的LP分解,形成了非冗余且完全重构的滤波器组,继承了小波变换和Contourlet变换的优点,更容易捕捉图像的几何结构和纹理特性. 鉴于WBCT的高频子带可以在任意方向上进行分解,给构建合理的系数树结构带来了一定困难,因此不宜采用基于树结构的编码算法. SPECK[19]是一种采用块结构的图像编码算法,该方法充分利用了小波系数的能量集中性和能量随尺度增加而衰减的特性,并结合子带内部不重要系数的相关性,将四叉树和位平面编码方法相结合,具有较好的压缩性能. 为此本文提出基于WBCT的SPECK图像编码算法,描述如下:
算法2 基于优化WBCT的SPECK图像编码算法(OW-SPECK算法)
(1) 选择合适的小波基(双正交小波基D9/7)对待压缩图像进行L级小波分解;
(2) 对获得的每个子带按照表 1进行视觉加权处理;
(3) 按照算法1确定每个小波子带的最优方向滤波分解数目;
(4) 按最优方向分解数目对每一小波子带进行方向滤波分解;
(5) 对分解后的各子带进行SPECK编码;
(6) 算法结束.
算法2流程图如图 5所示.
 |
| 图 5 算法2流程图Fig. 5 The flow chart of the algorithm 2 |
最后对得到的码流进行自适应算术编码. 解码时进行方向滤波分解逆运算和小波反变换并用视觉加权数据除对应子带得到重构图像.
4 实验结果及分析 4.1 编码效果对比实验为验证本文算法的有效性,以512×512的标准灰度图像Boat和Babara为例进行压缩实验. 小波基选取双正交小波基D9/7,分解级数L=4,方向分解重构滤波器则采用了pkva滤波器[20].
图 6给出了不同码率下本文算法和SPECK算法Boat重构图像的对比. 可以看出Boat图像具有明显的几何特征,由于本文算法对高频部分采用了基于熵的方向滤波优化分解,使得图像中的边缘和纹理等细节信息得到了很好的保留,因此在较高压缩比下重构图像依然保持了较清晰的效果. 当码率为0.25 b/p时,PSNR达到30 dB以上. 表 2给出了不同码率下本文算法和SPECK算法的PSNR对比.
 |
| 图 6 本文算法和SPECK算法Boat重构图像效果对比Fig. 6 Comparison of the reconstructed Boat images by the proposed algorithm and SPECK |
 | 0.05 | 0.10 | 0.125 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 |
| OW-SPECK | 24.34 | 26.58 | 27.37 | 28.21 | 29.37 | 30.26 | 31.05 | 31.78 | 32.42 |
| SPECK | 24.30 | 26.34 | 26.99 | 27.74 | 28.85 | 29.81 | 30.51 | 31.46 | 32.16 |
为进一步说明本文算法的优势,将本文算法分别与SPECK算法和CSPIHT算法[5]进行对比. 图 7给出了Babara图像不同码率下本文算法和SPECK算法重构图像的对比. 表 3给出了不同码率下本文算法和SPECK及CSPIHT算法的PSNR对比. 可以看出,本文算法在主观质量和PSNR两方面都明显好于SPECK算法. 这是由于本文算法采用基于熵的方向滤波优化分解,使得方向子带内部相关性增强,保留了更多的纹理特征. 与CSPIHT算法相比,由于Contourlet在方向滤波后,削弱了树形结构子带间系数的相关性,从而使CSPIHT的编码效率降低,而本文算法采用基于块的编码方式,因此表现出更好的压缩性能.
 |
| 图 7 本文算法和SPECK算法Babara重构图像效果对比Fig. 7 Comparison of the reconstructed Babara images by the proposed algorithm and SPECK |
此外,本文算法在局部的纹理细节上也表现出了良好的主观特性. 图 8为压缩码率等于0.25 b/p时SPECK算法和本文算法解压后的局部细节图像. 可以看出,SPECK算法的桌布纹理较为模糊,而本文算法的桌布纹理保留较好,更加清晰.
 |
| 图 8 局部压缩效果对比Fig. 8 Comparison of local compression effect |
SPECK与SPIHT是目前比较主流的两种低复杂度小波图像编码算法,二者核心的编码思想都是在比特平面上通过比较某一集合内的元素是否超过给定阈值,决定该比特平面输出的比特码流. 不同点在于SPECK算法以块状结构组织集合,而SPIHT以树状结构组织集合,二者编解码执行的主要操作都是比较判断,其算法复杂度均为O(n),具体耗时对于不同的图像会有一定差异. 本文提出的OW-SPECK算法是以SPECK算法为框架,编解码时间复杂度仍为O(n). 而文[5]提出的CSPIHT是以SPIHT算法为框架,编解码时间复杂度同样为O(n). 因此本文算法OW-SPECK没有增加复杂度,与SPECK、 SPIHT、 CSPIHT的复杂度在同一等级上.
为具体验证算法耗时情况,针对本文OW-SPECK算法,分别与SPECK和CSPIHT两种算法进行实验对比. 实验所用计算机硬件环境为: CPU型号为Intel Core i3双核2.2 GHz,内存容量4.0 GB; 软件环境为: 操作系统为Windows 7,Matlab软件版本为R2012b. 表 4给出了压缩码率为0.50 b/p时的耗时情况对比. 可以看出,由于引入基于熵的方向滤波优化分解,本文OW-SPECK算法较原始SPECK算法耗时略有增加,但低于同样采用Contourlet变换的CSPIHT算法.
| (单位: s) | |||
| (unit: s) | |||
 | CSPIHT | SPECK | OW-SPECK |
| Boat | 6.224 | 5.943 | 6.075 |
| Babara | 4.545 | 4.287 | 4.396 |
Contourlet将小波的优点延伸到高维空间,具有多分辨率、 局部化和各向异性等优良特性,是一种真正意义上的图像2维表示方法. 然而由于Contourlet变换具有冗余特性,给图像编码带来一定困难. 本文针对Contourlet方向滤波分解过程没有考虑子带内系数分布特性的问题,提出基于能量熵的子带方向滤波分解优化算法,使得各方向子带内部的局部相关性加强,而子带间相关性减弱. 在此基础上采用SPECK算法,按照集合分裂方式组织系数,并根据人眼视觉特性进行加权处理. 编码实验结果表明重构图像不仅峰值信噪比得到提高,而且对局部纹理失真明显减小,这说明将能量熵作为方向分解的依据是正确的. 本文算法的进一步改进应是根据方向优化分解后的小波系数分布情况按方向子带组织系数.
| [1] | 王相海, 孙强, 宋传鸣, 等. 基于多尺度几何分析的图像编码研究进展[J]. 计算机研究与发展, 2010, 47(6): 1132-1143. Wang X H, Sun Q, Song C M, et al. Advances in image coding based on multiscale geometric analysis[J]. Journal of Computer Research and Development, 2010, 47(6): 1132-1143. |
| [2] | Zhang S Y, Xue X C, Shi J X. Image compression based on Contourlet and no lists SPIHT[C]//IEEE International Conference on Computer, Mechatronics, Control and Electronic Engineering. Piscataway, NJ, USA: IEEE, 2010: 211-214. |
| [3] | Do M N, Vetterli M. Contourlets: A directional multiresolution image representation[C]//Proceedings of IEEE International Conference on Image Processing. Piscataway, NJ, USA: IEEE, 2002: 357-360. |
| [4] | Eslami R, Radha H. Wavelet-based Contourlet transform and its application to image coding[C]//Proceedings of IEEE International Conference on Image Processing. Piscataway, NJ, USA: IEEE, 2004: 3189-3192. |
| [5] | Eslami R, Radha H. Wavelet-based Contourlet coding using an SPIHT-like algorithm[C]//Proceedings of International Conference on Information Sciences and Systems. Piscataway, NJ, USA: IEEE, 2004: 784-788. |
| [6] | 王力, 王向阳. 应用人眼视觉特性的Contourlet 域图像压缩编码算法[J]. 计算机工程与应用, 2011, 47(22): 168-171. Wang L, Wang X Y. Image coding scheme based on Contourlet transform and human visual system[J]. Computer Engineering and Applications, 2011, 47(22): 168-171. |
| [7] | Hung C H, Hang H M. A reduced-complexity image coding scheme using decision-directed wavelet-based Contourlet transform[J]. Journal of Visual Communication & Image Representation, 2012, 23(2012): 1128-1143. |
| [8] | Fan Y H, Wang G, Liang X. A static image coding algorithm based on Contourlet classified hidden Markov tree model[J]. Engineering Computations: International Journal for Computer-Aided Engineering and Software, 2011, 28(2): 172-183. |
| [9] | Tamilarasi M, Palanisamy V. A novel embedded coding for medical image compression using Contourlet transform[J]. Internalional Journal of Signal and Imaging Systems Engineering, 2012, 5(3): 204-212. |
| [10] | 白璘, 刘盼芝, 李光. 一种基于Contourlet变换的高光谱图像压缩算法[J]. 计算机科学, 2012, 39(11A): 395-427. Bai L, Liu P Z, Li G. Hyperspectral images compression algorithm based on Contourlet transform[J]. Computer Science, 2012, 39(11A): 395-427. |
| [11] | Aul-Llins F. Entropy-based evaluation of context models for wavelet-transformed images[J]. IEEE Transactions on Image Processing, 2015, 24(1): 57-67. |
| [12] | Bamberger R H, Smith M J T. A filter bank for the Directional decomposition of images: Theory and design[J]. IEEE Transactions of Signal Processing, 1992, 40(4): 882-893. |
| [13] | Do M N, Vetterli M. Pyramidal directional filter banks and curvelets[C]//IEEE International Conference on Image Processing. Piscataway, NJ, USA: IEEE, 2001: 158-161. |
| [14] | Tobias G, Thomas G, Wolfgang R. Image content matched directional filters for image coding based on Contourlet transform[C]//IEEE Xplore-Picture Coding Symposium (PCS). Piscataway, NJ, USA: IEEE, 2013: 237-240. |
| [15] | Pham T D. Geostatistical entropy for texture analysis: An indicator kriging approach[J]. International Journal of Intelligent Systems, Special Issue: Advances in Intelligent Systems, 2014, 29(3): 253-265. |
| [16] | Adzic V, Hock H S, Kalva H. Visually lossless coding based on temporal masking in human vision[J]. Proceedings of SPIE-The International Society for Optical Engineering, 2014, 9014(10): 2458-2462. |
| [17] | Miloslavski M, Ho Y S. Zerotree wavelet image coding based on the human visual system model[C]//IEEE Asia-Pacific Conference on Circuits and Systems. Piscataway, NJ, USA: IEEE, 1998: 57-60. |
| [18] | Kim J Y, Kim L S. An advanced contrast enhancement using partially overlapped sub-block histogram equalization[J]. IEEE Transactions on Circuits and Video Technology, 2001, 11(4): 475-484. |
| [19] | Pearlman W A, Islam A, Nagaraj N, et al. Efficient, low-complexity image coding with a set-partitioning embedded block coder[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2004, 14(11): 1219-1235. |
| [20] | Duncan D Y, Do M N. Directional multiscale modeling of images using the Contourlet transform[C]//IEEE Workshop on Statistical Signal Processing. Piscataway, NJ, USA: IEEE, 2003: 262-265. |




