2. 东北大学流程工业综合自动化国家重点实验室, 辽宁 沈阳 110819
2. National Key Laboratory of Integrated Automation for Process Industries, Northeastern University, Shenyang 110819, China
1 引言
众所周知,模型预测的精确性直接决定了优化结果的可靠性,为了更好地实现采油过程的优化控制,需对优化起关键作用的指标——吨油综合能耗——进行精确预测. 刘潭等[1]建立的吨油综合能耗混合模型在一定程度上提高了吨油综合能耗的预测精度,但由于油气生产过程中一些不确定信息的影响,该模型仍存在误差. 因此,如何实现对采油过程吨油综合能耗混合模型的误差补偿是目前亟待解决的问题.
为实现对吨油综合能耗混合模型的误差补偿,需对误差的分布特性进行准确描述[2],由于实际生产过程误差不一定服从正态分布,故单高斯(正态)模型不能很好地描述误差分布特性. 作为单高斯模型的延伸,高斯混合模型(GMM)可用来估计任意分布的概率密度函数[3],且已经在语音、 图像识别等领域,取得了较为显著的效果[4, 5, 6, 7]. 因此,本文在文[1]所建立的模型基础上,从一个较新角度出发,利用GMM模型描述模型的误差特性. 基于传统期望最大化(EM)算法[6]估计GMM的参数时,参数估计的性能受初始化影响大,易于陷入局部极值[8],且在样本有限时,易出现过拟合问题,使得泛化能力降低. 为了解决这些问题,一些研究者已经将模拟自然进化过程来搜索最优解的遗传算法[9, 10, 11, 12]应用到GMM的参数估计中,并在实践中取得了一定的效果. 但这些成果均是单独采用遗传算法,导致寻优能力和收敛速度不佳,特别是局部寻优能力不足.
针对传统算法估计GMM参数时存在的不足,本文进行了如下改进:
(1) 将对GMM泛化能力起决定作用的结构尺寸和参数作为整体进行优化;
(2) 在已有的参数辨识算法[12]基础上,融入了局部优化方法的思想,对EM算法做了以下改进: 首先将梯度算子引入到遗传算法(GA)中,与交叉、 变异算子组成混合算子,构成基于梯度的混合遗传算法(GGA). 然后将GGA引入到EM算法形成GGA-EM算法. 进而提出了一种基于GGA-EM算法的GMM误差补偿方法. 最后,将提出的模型误差补偿方法应用到某个采油作业区的一个区块油气生产过程中,结果表明该方法可以有效地提高模型的预测精度,为作业区采油过程的优化控制奠定了坚实基础.
2 油气生产吨油综合能耗混合模型本文以某个采油作业区某一个整体区块为背景,其油气生产过程如图 1所示.
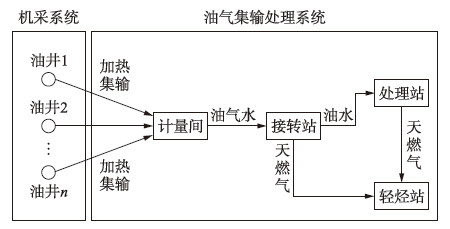 |
| 图 1 油气生产过程基本流程图Fig. 1 Basic flow chart of oil and gas production process |
从图中可以看出,该生产过程主要包括机采系统和油气集输处理系统. 基本流程为: 油井产出的油气水混合液体经过井口加热炉加热后通过集输管道被送至计量间进行计量,然后输送到接转站进行气液分离. 分离出来的天然气经输气管道被输送至轻烃站进行处理回收,而分离出来的油水混合液经输油管道被输送至原油处理站进行原油脱水、 原油稳定等相应处理,最终脱水原油入库或外输. 其中,综合能耗主要指机采系统的动力消耗(电耗)和集输系统的热力消耗(天然气消耗)和动力消耗(电耗).
吨油综合能耗即为整个采油系统生产1吨原油的能源消耗,由于整个采油过程较为复杂,且一些假设条件的存在,使得建立采油过程吨油综合能耗机理模型存在较大误差,混合模型[1]是将机理模型与基于最小二乘支持向量机的数据模型相结合而成的,其结构图如图 2所示.
 |
| 图 2 混合模型结构图Fig. 2 Structure of hybrid model |
该模型是利用机理模型对油气生产过程的整体特性进行描述,再利用最小二乘支持向量机(LS-SVM)模型对未建模部分的误差进行补偿,模型输出表示如下:

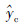 为混合模型预测输出,
为混合模型预测输出,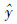 为机理模型输出,
为机理模型输出,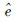 是LS-SVM模型对实际值与机理模型输出的误差估计.
是LS-SVM模型对实际值与机理模型输出的误差估计.
对于LS-SVM误差模型,选取 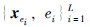 为样本集,其中
为样本集,其中 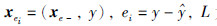 为样本数. xe-为相应的操作向量,由采油区块平台中每口抽油机井冲程、 冲次、 井口加热温度和输油泵扬程组成,y为相应的吨油综合能耗实际输出值.
为样本数. xe-为相应的操作向量,由采油区块平台中每口抽油机井冲程、 冲次、 井口加热温度和输油泵扬程组成,y为相应的吨油综合能耗实际输出值.
混合模型不仅充分考虑了过程的物理特性也利用了相关的数据信息,可对油气生产过程综合能耗较为准确预测,但仍然存在模型误差. 为进一步提高模型的预测精度,提出了基于GGA-EM算法的GMM的吨油综合能耗混合模型误差补偿方法.
3 基于改进高斯混合模型(GMM)的预测误差补偿GMM是一种能够对误差分布特性进行描述,进而实现对模型校正的一种方法. 通过对油气生产过程综合能耗混合模型描述可以看出混合模型能够较好地跟踪过程输出,但仍存在一定误差. 因此,为了进一步提高模型的预测准确性,本文采用GMM对模型误差特性进行描述,并针对传统EM算法在GMM参数估计时存在的不足,提出了一种基于改进算法的GMM模型误差补偿方法.
3.1 高斯混合模型描述假设一批数据每个点均由一个单高斯分布生成(具体参数μj,Σj未知),而这一批数据共由M个单高斯模型生成,具体某个数据xi属于哪个单高斯模型未知,且每个单高斯模型在混合模型中占的比例αj未知,将所有来自不同分布的数据点混在一起,该分布称为高斯混合分布如图 3所示.
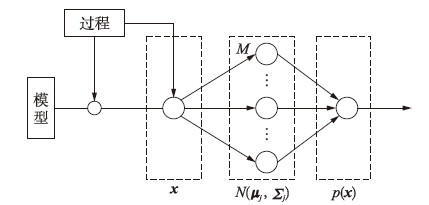 |
| 图 3 高斯混合模型原理图Fig. 3 GMM principle diagram |
从数学上讲,我们认为这些数据的概率分布密度函数可以通过加权函数表示[13]:
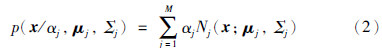
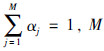 为高斯混合模型中包含单高斯模型的个数,其中
为高斯混合模型中包含单高斯模型的个数,其中 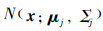 为
为
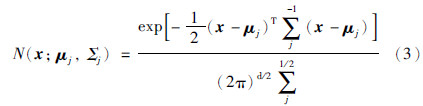
令模型的参数θj={αj,μj,Σj,j=1,2,…,M},可通过样本集X来估计高斯混合模型的所有参数: θ=(θ1,…,θM)T,根据极大似然准则构造相应的似然函数为

(1) 初始化: 由K均值聚类算法对样本进行聚类,利用各类的均值作为μj0,并计算Σj0,αj0取各类样本占样本总数的比例.
(2) 估计步骤(E-step): 令αj的后验概率为
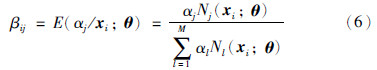
对于每个单高斯模型分别用式(3)计算每个样本点xi在该模型下的概率密度值Nj(xi; θ),对于所有样本,得到一个n×1的向量,计算M次,得到n×M的矩阵,每一列为所有点在该模型下的概率密度值,实现 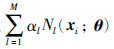 时,即得到每个点在所有单高斯模型下的概率密度分布函数.
时,即得到每个点在所有单高斯模型下的概率密度分布函数.
(3) 最大化步骤(M-step): 将期望最大化,更新混合权值,均值及方差矩阵如下:

(4) 收敛条件: 不断地迭代E和M步骤,重复更新式(7)~(9),直到参数的变化不显著,即|θ-θ|′<ε,或达到最大迭代次数,θ′为更新后的参数,这里ε=10-5.
高斯混合模型中单高斯模型个数M的选择非常重要,如果M过大,会导致过度拟合,M过小往往导致欠拟合. 对于M的优化,一些性能准则被提出,如:Akaike信息准则[16]、 贝叶斯信息准则[17]等. 一般通常采用贝叶斯准则对M进行优化求解,其公式为
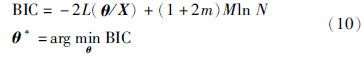
由于希望求解函数最小值,根据实际需要,目标函数[18]可由式(11)构成:
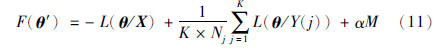
从式(11)可知,由于在目标函数中加入了有关模型复杂度的惩罚项αM. 该项可以保证在求解模型参数同时,自动找到合适的单高斯模型个数,使M不至过大,从而获得一个鲁棒性好、 抗噪能力强的GMM结构,有效克服过拟合问题.
应用提出的GGA-EM算法对F(θ′)优化,进而实现对GMM的参数估计,其对应的估计流程如图 4所示.
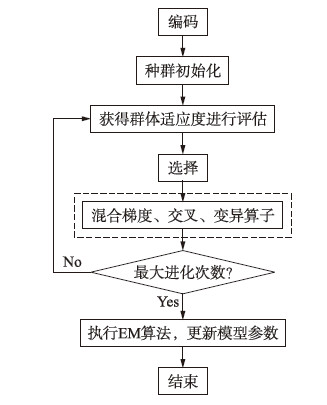 |
| 图 4 基于GGA-EM算法的参数估计流程图Fig. 4 Flow chart of parameter estimation based on GGA-EM algorithm |
对于编码,在遗传训练的过程中采用实数编码方式; 对于种群初始化,首先使用K均值算法产生的初始参考模型θ0,其次,在参考模型θ0的基础上对种群进行初始化; 在选择操作中,采用抽样误差最小、 应用无回放余数随机采样选择法(RSSR)对个体进行选择,同时采用最优个体保留法,以保证算法的收敛性; 在遗传操作中,本文提出了基于梯度、 交叉、 变异混合操作算子,可由式(12)表示:
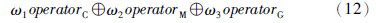
式(12)表示新一代种群分别由概率为ω1的交叉算子,概率为ω2的变异算子和概率为ω3梯度算子产生. 对于交叉、 变异算子及相应的交叉和变异概率,采用文[19]中方法进行计算,且相关参数设置与参考文献保持一致,而对于梯度算子,计算公式如下:
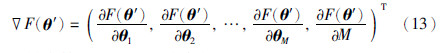
由梯度算子进而可得搜索方向为

则由梯度操作算子产生的新一代种群可以表示为
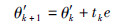
tk为相应的步长,可由式(15)计算:

式中,t0为初始步长,gen为迭代次数. 如果函数F(θ′)有界,即{θ′∈RnF(θ′)≤F(θ′*)},则由梯度下降法产生的序列θ′(k)保持有界,且至少有一个点为Pareto临界点[20]. 显然容易得到本文的函数可以收敛到一个全局最优点.
由式(12)不难看出,由于混合算子中交叉、 变异算子的存在,不仅维持群体的多样性,而且由于梯度算子的加入,很大程度提高了算法的局部搜索能力.
上述遗传过程将一直进行直至到达预定的最大迭代次数为止. 在遗传优化结束后,最优的GMM模型再将所有的训练样本应用EM算法进行训练直至收敛.
3.3 基于GGA-EM算法的高斯混合模型预测误差补偿将混合模型误差和过程的操作变量作为GMM输入变量向量,即:
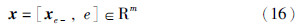
其中,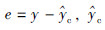 为混合模型预测输出值,xe-=[xe1,xe2,…,xem]⊂[x1,x2,…,xn]为除模型误差外的过程操作变量.
为混合模型预测输出值,xe-=[xe1,xe2,…,xem]⊂[x1,x2,…,xn]为除模型误差外的过程操作变量.
相应的条件误差概率分布函数:
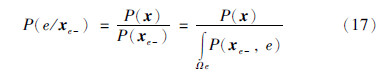
其中,P(xe-)为式(2)定义的高斯混合模型联合概率密度分布; P(e/xe-)为xe-下偏差的条件概率分布. 通过计算可得到条件误差均值μe/xe-和条件误差方差σ2e/xe-由式(18)、式(19)所示:

μe/xe-表明预测输出的偏移量,σ2e/xe-可以指示模型预测结果的可靠性.
由于预测偏差为模型预测值和实际测量值之间的偏差,直接利用条件误差均值对模型输出进行校正,可以提高整个模型预测结果的准确性.
基于GGA-EM算法的GMM对综合能耗混合模型的预测误差进行补偿采用如图 5所示的并行结构,两者输出迭加后作为整个模型输出:
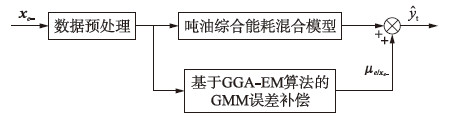 |
| 图 5 基于GGA-EM算法的高斯混合模型输出误差补偿Fig. 5 Output error compensation of GMM based on GGA-EM algorithm |

 即为基于GMM误差补偿后模型输出值.
4 仿真验证
即为基于GMM误差补偿后模型输出值.
4 仿真验证
为了验证基于GGA-EM算法的GMM误差补偿模型的预测效果,以某个采油作业区中由6口抽油机井构成的一个区块生产过程为例进行仿真验证. 将收集到的现场数据经过预处理得到700组有效数据,其中600组作为训练样本,100组作为测试样本. 其中,x=[xe-,e]=[si,ni,Twi,H,ei=1,2,…,6]为GMM输入变量向量,即过程测量变量和吨油综合能耗混合模型预测误差组成,共25个变量.
GGA算法参数设置如下: 种群数量N′p=20,进化代数gen=20,种群初始化时随机产生单高斯模型个数低于30的高斯混合模型. 梯度操作算子执行概率ω3=1,梯度操作初始步长t0=0.1.
首先采用传统EM算法和贝叶斯信息准则优化GMM结构,EM最大迭代次数tMAX=20,得到当M=17时BIC的值最小,此时,最佳的混合高斯模型由17个单高斯模型组合而成. 当M=17时,最终采用EM算法对GMM参数θ估计收敛时,最大迭代次数为39.
在同样条件下,采用提出的GGA-EM算法优化目标函数式(11),得到M=14.
为了验证基于GGA-EM算法的GMM误差补偿模型具有较好的预测性能,将混合模型、 基于GMM误差补偿模型以及基于GGA-EM算法的误差补偿模型分别应用该区块进行仿真,结果如图 6所示.
 |
| 图 6 吨油综合能耗预测结果比较Fig. 6 Comparison of comprehensive energy consumption for per ton oil prediction results |
由图 6可以看出,虽然混合模型能对过程的趋势有较好的预测效果,但仍存在一定的误差,而基于GMM误差补偿和基于GGA-EM算法的GMM误差补偿后,预测效果显著提高.
为了进一步验证基于GGA-EM算法的GMM误差补偿模型具有较优的预测性能,对3种方法的预测平均绝对误差(MAE)、 均方根误差(RMSE)和平均绝对百分比误差(MAPE)性能指标进行计算,并对结果进行比较,见表 1.
| 模型 | MAE | RMSE | MAPE |
| 混合模型 | 1.685 5 | 1.114 9 | 1.596 8 |
| GMM误差补偿模型 | 0.551 3 | 0.798 4 | 0.842 8 |
| 基于GGA-EM算法的GMM误差补偿模型 | 0.386 0 | 0.546 5 | 0.593 0 |
由表 1知,本文提出的基于GGA-EM算法的GMM误差补偿模型的各性能指标明显小于混合模型,并在一定程度上优于采用传统的EM算法优化的GMM误差补偿模型. 同时,本文提出的误差补偿方法得到的最佳单高斯模型个数少于基于传统EM算法的GMM误差补偿方法,提高了计算效率. 进而证明了本文提出的误差补偿模型具有更高的预测精度和高效性.
5 结论吨油综合能耗是采油过程一个重要的经济指标,为了获得更为精确的综合能耗预测值,本文利用高斯混合模型(GMM)来实现对综合能耗混合模型的误差补偿. 并针对传统EM算法在GMM的参数估计时易于陷入局部极小值且存在过拟合的问题,对GMM的结构与参数共同进行优化,可有效地避免过拟合,增强模型在小训练样本集下的泛化能力,且提出了一种GGA-EM的参数估计算法,该算法弥补了传统EM算法在参数估计时存在的不足. 最后,将提出的模型误差补偿方法应用到某采油作业区的一个区块采油过程中,结果表明该方法可以有效地提高模型的预测精度和可靠性,并与标准的GMM误差补偿方法相比,不仅预测性能上有一定优势,且同时提高了计算效率.
| [1] | 刘潭, 高宪文, 王丽娜. 油气生产过程综合能耗混合建模方法[J]. 东北大学学报: 自然科学版, 2013, 34(11): 1525-1528. Liu T, Gao X W, Wang L N. Hybrid modeling method of comprehensive energy consumption for oil and gas production process[J]. Journal of Northeastern University: Natural Science, 2013, 34(11): 1525-1528. |
| [2] | 田中大, 李树江, 王艳红, 等. 基于ARIMA补偿ELM的网络流量预测方法[J]. 信息与控制, 2014, 43(6): 705-710. Tian Z D, Li S J, Wang Y H, et al. Network traffic prediction method based on extreme learning machine with ARIMA compensation[J]. Information and Control, 2014, 43(6): 705-710. |
| [3] | Yang Y Y, Mahdi M. Probabilistic characterization of model error using Gaussian mixture model-with application to Charpy impact energy prediction for alloy steel[J]. Control Engineering Practice, 2012, 20(1): 82-92. |
| [4] | He Y, Pan W, Lin J Z. Cluster analysis using multivariate normal mixture models to detect differential gene expression with microarray data[J]. Computational Statistics & Data Analysis, 2006, 51(2): 641-658. |
| [5] | Zivkovic Z, van der Heijden F. Efficient adaptive density estimation per image pixel for the task of background subtraction[J]. Pattern Recognition Letters, 2006, 27(7): 773-780. |
| [6] | Huang Z K, Chau K W. A new image thresholding method based on Gaussian mixture model[J]. Applied Mathematics and Computation, 2008, 205(2): 899-907. |
| [7] | Kinnunen T, Saastamoinen J, Hautamki V, et al. Comparative evaluation of maximum a Posteriori vector quantization and Gaussian mixture models in speaker verification[J]. Pattern Recognition Letters, 2009, 30(4): 341-347. |
| [8] | Li Y, Li L. A novel split and merge EM algorithm for Gaussian mixture model[C]//Proceedings of the 5th International Conference on Natural Computation. Piscataway, NJ, USA: IEEE, 2009: 479-483. |
| [9] | Tang K S, Man K F, Kwong S, et al. Genetic algorithm and their applications[J]. IEEE Signal Processing Magazine, 1996, 13(6): 22-37. |
| [10] | Gabrys B, Ruta D. Genetic algorithms in classifier fusion[J]. Applied Soft Computing, 2006, 6(4): 337-347. |
| [11] | Hong Q Y, Kwong S. A genetic classification method for speaker recognition[J]. Engineering Applications of Artificial Intelligence, 2005, 18(1): 13-19. |
| [12] | Pernkopf F, Bouchaffra D. Genetic-based EM algorithm for learning Gaussian mixture models[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(8): 1344-1348. |
| [13] | Bishop C M. Pattern recognition and machine learning[M]. Berlin, Germany: Springer, 2007: 10. |
| [14] | Reynolds D A, Rose R C. Robust text 2 independent speaker identification using Gaussian mixture speaker models[J]. IEEE Transactions Speech Audio Processing, 1995, 3(1): 72-83. |
| [15] | Stauffer C, Grimson W. Learning patterns of activity using real-time tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(8): 747-757. |
| [16] | Akaike H. A new look at the statistical model identification[J]. IEEE Transations on Automatic Control, 1986, 34(3): 276-280. |
| [17] | Knoishi S, Kitagawa G. Information criteria and statistical modeling[M]. Berlin, Germany: Springer, 2007. |
| [18] | 崔玉红, 胡光锐, 何旭明. 基于混合进化计算的GMM优化方法及其在说话人辨认中的应用[J]. 应用科学学报, 2002, 20(2): 142-143. Cui Y H, Hu G R, He X M. Optimization of GMM based on hybrid evolutionary algorithm and its application in speaker identification[J]. Journal of Applied Sciences, 2002, 20(2): 142-143. |
| [19] | Lin L, Wang S X. A new genetically optimized GMM for speaker recognition[C]//Proceedings of the 6th World Congress on Intelligent Control and Automation. Piscataway, NJ, USA: IEEE, 2006: 10236-10239. |
| [20] | JoÉrg F, Benar F S. Steepest descent methods for multi-criteria optimization[J]. Mathematical Methods of Operations Research, 2000, 51(3): 479-494. |



