1 引言
网络化控制系统(networked control system,NCS)是指通过数字网络形成的空间分布式闭环控制系统[1, 2, 3]. 在NCS中,控制器与传感器、 执行器等系统组件通过通信网络进行数据交换. 由于网络通信带宽限制,在每个采样周期只有部分传感器和执行器可获得网络资源与远程控制器进行通信,这称为介质访问约束. 介质访问约束现象主要存在于具有数量众多的传感器/执行器(或子系统)和有限通信网络的大系统中,如海面溢油监测系统、 复杂工业过程控制系统等[4, 5, 6]. 介质访问约束使得系统无法及时获取测量信息和执行控制命令,从而导致系统性能下降甚至不稳定.
目前,具有介质访问约束的NCS得到广泛的研究[7, 8, 9, 10]. 文[11]采用静态周期通信序列来描述传感器和执行器的介质访问状态,并通过求解一个组合优化问题得出最优的通信序列. 文[12]研究了带有访问约束和数据包丢失的网络化系统H∞控制问题. 而文[13]针对具有介质访问约束的网络化系统,研究了最优线性滤波器的设计问题. 近来,文[14]研究了周期通信调度的实现方式,提出了一种反馈控制器与调度策略的协同设计方法. 随后,这种协同设计方法在文[15]中被扩展到同时具有访问约束和常数时延的网络化系统. 然而,上述周期性的调度策略虽然很容易实现,但不利于提高网络的利用率. 基于这个问题,文[16]针对访问约束、 时延和量化等多种通信限制共存的网络化系统,首次在非解耦的情况下研究了控制器与传感器/执行器通信调度的联合设计问题. 文[17]针对一类具有通信约束的随机时延网络控制系统,提出了一种基于最大加权误差优先传输的动态调度策略与鲁棒状态反馈控制器的协同设计方法. 文[16, 17]中的通信调度都是基于状态信息在线确定的,因此可以实现网络通信资源的充分利用.
由于网络通信协议、 网络负载分布等多种因素的复合影响,网络访问约束常常呈现出复杂的随机特性. 此时,现存的控制器与网络通信调度的联合设计研究结果已不再适用. 基于此,文[18]针对具有访问约束和时延的NCS,在执行器的介质访问状态由马尔可夫过程驱动的情况下,给出了模式及时滞依赖的状态反馈控制器设计方法. 但该文的研究主要集中在网络化系统的稳定化控制方面,没有对系统的控制性能产生足够的重视. 文[19]考虑了网络化系统中的随机信道访问约束,提出了有限及无限时域内最优控制器设计方法,实现系统的均方指数稳定. 然而,该文仅仅考虑执行器端的访问约束情况,并且假设系统状态是直接可测量的,这在大多数控制系统中很难实现.
本文针对随机事件驱动通信的NCS,假设介质访问约束同时存在于输入和输出信道,根据控制器与执行器/传感器的随机通信机制将系统建模为马尔可夫线性跳变系统; 然后基于分离原理,分别给出了状态估计和最优控制器的设计方法,通过卡尔曼滤波器对状态进行估计,然后利用状态估计值构造最优控制律使得闭环系统渐近稳定. 最后,通过算例验证了本文方法的正确性和有效性.
符号说明: Rn表示实数域上的n维Euclidean空间; P>0(P≥0)表示P为对称正定(半正定)矩阵; Cβα为从α个元素中选取β个元素的组合数; XT与X-1分别表示矩阵X的转置和逆; tr X表示求矩阵X的迹; {Xi}i=1N表示矩阵X1,X2,…,XN的集合; E(γ)和P(γ)分别表示随机过程γ的数学期望和概率; 定义Z={0,1,2,…}为非负整数的集合; 定义T={0,1,…,T-1},N1={1,2,…,N1},N2={1,2,…,N2},其中T、 N1和N2都为正整数.
2 系统描述本文研究的NCS结构如图 1所示,介质访问约束存在于传感器与控制器、 控制器与执行器之间.
 |
| 图 1 网络化控制系统结构Fig. 1 The structure of the NCS |
图 1中,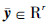 和
和  分别为控制器的输入和输出. 该NCS共有m个执行器和r个传感器. 由于网络带宽的限制,每个采样周期仅有p个执行器和q个传感器可以接入网络并进行数据传输,其中,1≤p
分别为控制器的输入和输出. 该NCS共有m个执行器和r个传感器. 由于网络带宽的限制,每个采样周期仅有p个执行器和q个传感器可以接入网络并进行数据传输,其中,1≤p
被控对象的数学模型为
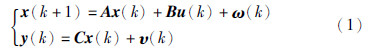
其中,x∈Rn、 u∈Rm、 y∈Rr分别表示被控对象的状态变量、 控制输入和测量输出; ω(k)∈Rn和υ(k)∈Rr是零均值的高斯过程,其方差矩阵分别为Q>0,R>0; 系统初始状态x0是均值为 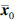 和方差阵为S0≥0的高斯随机向量,而且ω(k)、 υ(k)和x0是相互独立的; A、 B、 C是常数矩阵.
和方差阵为S0≥0的高斯随机向量,而且ω(k)、 υ(k)和x0是相互独立的; A、 B、 C是常数矩阵.
在NCS的执行器端,引入一个二值函数δi(k)来表示k时刻执行器的介质访问状态:

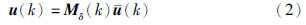
假设在相邻的两个采样周期Mδ(k)的切换服从马尔可夫随机过程,并且Mδ(k)从有限集{Miδ}i=1N1中取值,满足以下条件概率:

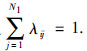 各个模态的初始概率分布为λ0=[λ1(0),…,λN1(0)]T,各个模态在k时刻的概率分布为λ(k)=[λ1(k),…,λN1(k)]T,且有λ(k+1)=λTλ(k). 为了简化问题描述,定义一个马尔可夫链{τ(k); k∈Z},满足τ(0)=τ0,τ(k)∈N1. 当Mδ(k)=Miδ时,有τ(k)=i. 则由式(2)可得
各个模态的初始概率分布为λ0=[λ1(0),…,λN1(0)]T,各个模态在k时刻的概率分布为λ(k)=[λ1(k),…,λN1(k)]T,且有λ(k+1)=λTλ(k). 为了简化问题描述,定义一个马尔可夫链{τ(k); k∈Z},满足τ(0)=τ0,τ(k)∈N1. 当Mδ(k)=Miδ时,有τ(k)=i. 则由式(2)可得
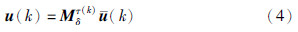
在NCS的传感器端,同样引入另一个二值函数θs(k)来表示k时刻传感器的介质访问状态:


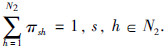 同理,可定义另一个独立的马尔可夫链{σ(k); k∈Z},σ(k)∈N2,来描述Mθ(k)的切换过程. 则控制器得到的被控对象输出为
同理,可定义另一个独立的马尔可夫链{σ(k); k∈Z},σ(k)∈N2,来描述Mθ(k)的切换过程. 则控制器得到的被控对象输出为

假设在第k个采样周期内,输入和输出信道获得介质访问权的执行器和传感器的模态是可检测的. 因此,可定义在k时刻已知的信息集为
 显然,
显然, .
.
联立式(1),式(4),式(6)可得NCS的广义被控对象模型为
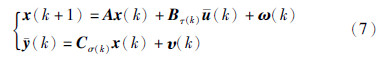
本节主要为系统(7)设计一个最优状态估计器. 令  表示k时刻系统状态x(k)的估计值,e(kk)表示估计误差,S(kk)表示估计误差方差阵,即
表示k时刻系统状态x(k)的估计值,e(kk)表示估计误差,S(kk)表示估计误差方差阵,即
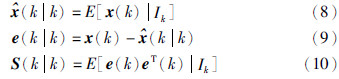
定理1 对于系统(7),存在如下递推的最优线性估计器:
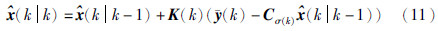
其中,

且有

证明 定义状态一步预测值为
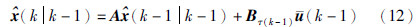
则状态一步预测误差为
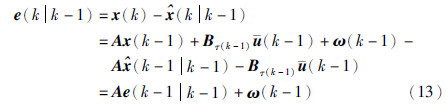
状态一步预测误差方差阵为
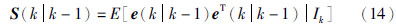
定义状态估计器为
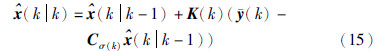
接下来的任务是在最小化目标函数J=E[e(k)eT(k)Ik]的基础上确定最优滤波增益矩阵K(k).
综合考虑式(9)、 式(13)和式(15),可得
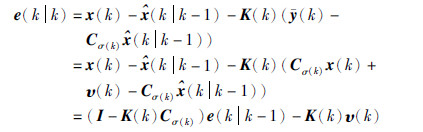
考虑到e(kk-1)和υ(k)线性无关,由式(10)和式(14)可得
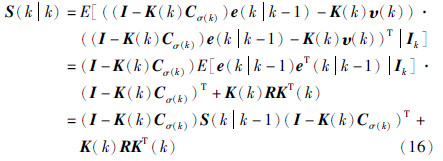
给式(16)加上和减去 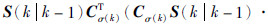
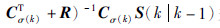 并进行整理,可得
并进行整理,可得
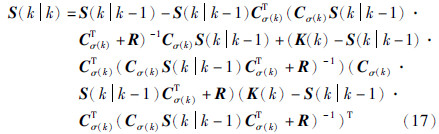
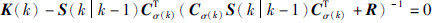 即可,于是可得
即可,于是可得

此时,估计误差方差阵


定理得证.
4 最优状态反馈控制器
得到系统状态x(k)的最优线性估计值 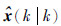 后,接下来的工作就是在初始条件为
后,接下来的工作就是在初始条件为  时,为系统(7)设计最优控制序列
时,为系统(7)设计最优控制序列 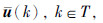 最小化二次型性能指标
最小化二次型性能指标
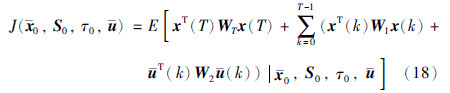
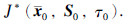
在给出系统(7)的最优控制器前,首先介绍一个预备引理[20].
引理1 对于矩阵F,G≥0,且满足G,F∈Rn×n,有以下等式成立
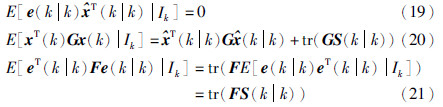
定理2 对于系统(7),使得性能指标(18)式最小化的控制律由式(22)给出

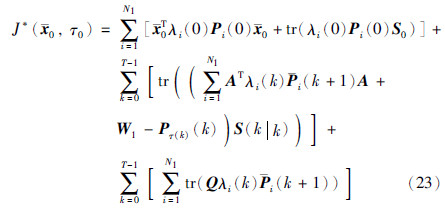


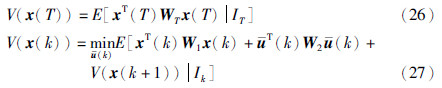

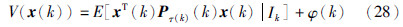
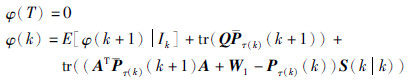
接下来通过推导式(28)成立来证明定理2. 已知在k=T时刻,Pτ(T)(T)=WT,τ(T)∈N1,φ(T)=0,式(28)显然成立; 假设在k+1时刻式(28)仍然成立,即
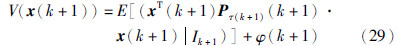
那么在k时刻,最优值函数为

将式(29)代入式(30),并考虑条件均值的平滑特性,可得


假设对于任意的测量函数f和g,有以下等式成立
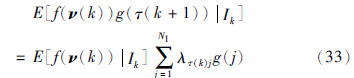
考虑过程噪声ω(k)的独立性,对式(32)求取数学期望,并应用引理1和式(33),可得


考虑到控制输入  无约束,令
无约束,令
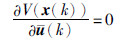
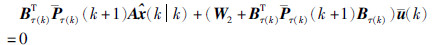
显然,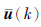 的系数矩阵为正定的,因此可得最优控制律为
的系数矩阵为正定的,因此可得最优控制律为
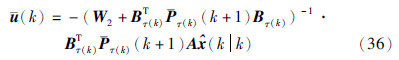
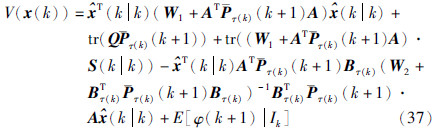
对式(37)再次应用引理1,可得
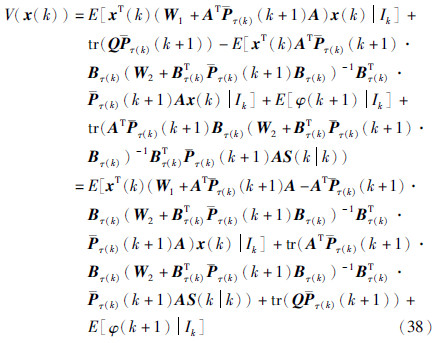
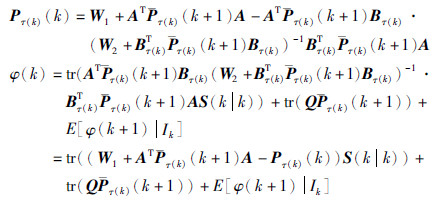

这说明在k时刻式(28)仍然成立. 由 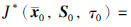 V(x(0)),可得
V(x(0)),可得

考虑一个开环不稳定的被控对象,其线性离散状态方程具有如下参数:
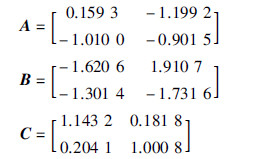
这里考虑最极端的介质访问约束情形,在控制器和执行器、 传感器和控制器之间分别只有一个通信信道可以进行数据传输,即有p=1,q=1. 此时执行器和传感器的介质访问序列集分别为
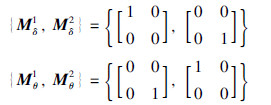
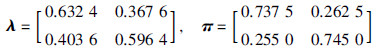
本文的目的是设计状态反馈控制器,使得系统(7)渐近稳定,并且最小化二次型性能指标式(18). 选择系统初始状态x0的期望值为 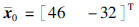 ,其方差阵S0=0.25I2×2; 选取WT=5I2×2,W1=5I2×2,W2=2I2×2. 图 2和图 3分别给出了执行器和传感器采用的马尔可夫介质访问序列,其中“1”和“2”为介质访问序列矩阵的编号. 最后,利用定理1和定理2进行状态估计并求取最优控制序列,可得系统状态响应和估计误差曲线分别如图 4和图 5所示. 仿真结果表明在本文设计的最优状态估计和控制器作用下,系统是渐近稳定的.
,其方差阵S0=0.25I2×2; 选取WT=5I2×2,W1=5I2×2,W2=2I2×2. 图 2和图 3分别给出了执行器和传感器采用的马尔可夫介质访问序列,其中“1”和“2”为介质访问序列矩阵的编号. 最后,利用定理1和定理2进行状态估计并求取最优控制序列,可得系统状态响应和估计误差曲线分别如图 4和图 5所示. 仿真结果表明在本文设计的最优状态估计和控制器作用下,系统是渐近稳定的.
 |
| 图 2 执行器随机介质访问序列Fig. 2 Stochastic medium access sequence of actuators |
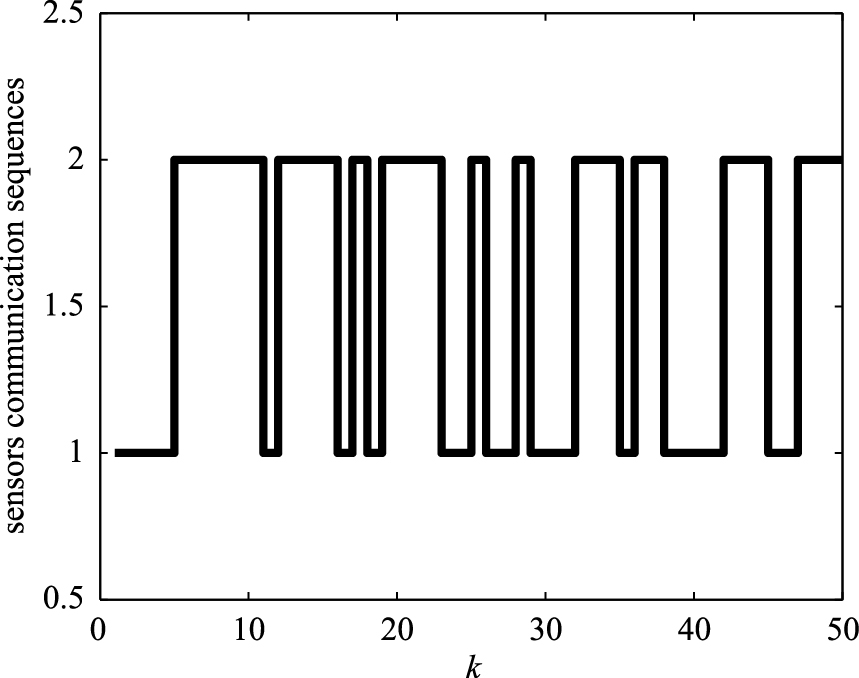 |
| 图 3 传感器随机介质访问序列Fig. 3 Stochastic medium access sequence of sensors |
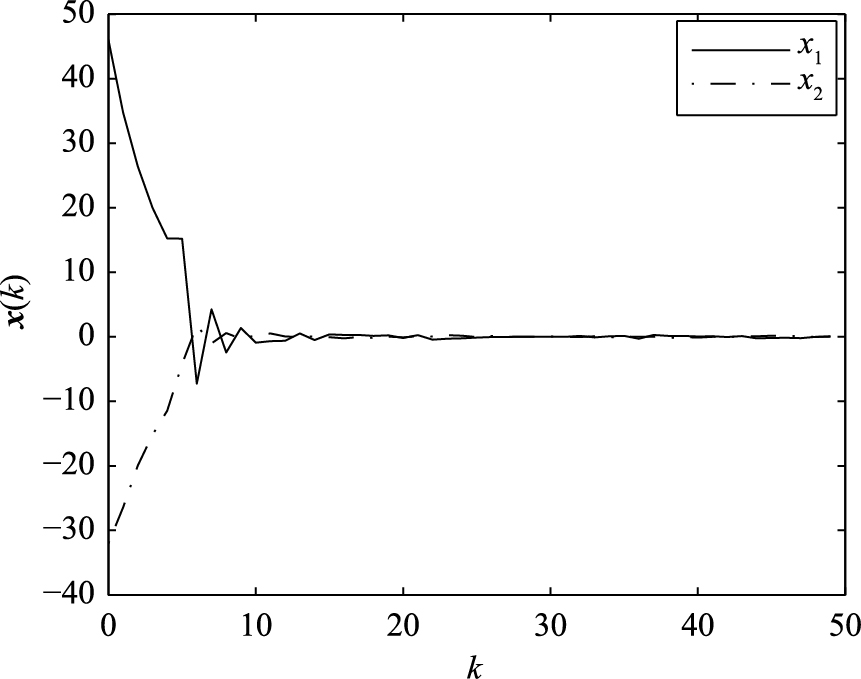 |
| 图 4 NCS的状态响应Fig. 4 State response of NCS |
 |
| 图 5 状态估计误差轨迹Fig. 5 Trajectories of state estimation errors |
本文针对随机事件驱动通信的网络化系统,研究了系统建模及最优估计和状态反馈控制器的设计问题. 根据执行器/传感器与控制器的随机通信机制将系统建模为马尔可夫线性跳变系统,在此基础上提出了最优估计器和状态反馈控制器的设计方法以保证闭环网络化控制系统的渐近稳定. 仿真结果表明,本文所提出的方法是有效的. 下一步的工作重点是在随机介质访问条件下,针对时延、 量化等通信约束共存的NCS,进行系统稳定性分析与控制综合; 此外,在多包数据传输条件下进行稳定控制器的设计,也是一个值得深入研究的方向.
| [1] | Hespanha J P, Xu Y G. A survey of recent results in networked control systems[J]. Proceedings of the IEEE, 2007, 95(1): 138-162. |
| [2] | Gupta R A, Chow M Y. Networked control system: Overview and research trends[J]. IEEE Transactions on Industrial Electronicsp, 2010, 57(7): 2527-2535. |
| [3] | 游科友, 谢立华. 网络控制系统的最新研究综述[J]. 自动化学报, 2013, 39(2): 101-108. You K Y, Xie L H. Survey of recent progress in networked control systems[J]. Acta Automatica Sinica, 2013, 39(2): 101-108. |
| [4] | Guo G, Lu Z B. Control with Markov sensors/actuators assignment[J]. IEEE Transactions on Automatic Control, 2012, 57(7): 1799-1804. |
| [5] | Meier L, Peschon J, Dressler R. Optimal control of measurement subsystems[J]. IEEE Transactions on Automatic Control, 1967, 12(5): 528-536. |
| [6] | Yang T C. Networked control system: A brief survey[J]. IET Proceedings-Control Theory and Applications, 2006, 153(4): 403-412. |
| [7] | Xue B, Li N, Li S, et al. Moving horizon scheduling for networked control systems with communication constraints[J]. IEEE Transactions on Industrial Electronics, 2013, 60(8): 3318-3327. |
| [8] | Gaid B M M, Cela A, Hamam Y. Optimal integrated control and scheduling of networked control systems with communication constraints: Application to a car suspension system[J]. IEEE Transactions on Control Systems Technology, 2006, 14(4): 776-787. |
| [9] | Longo S, Herrmann G, Barber P. Robust scheduling of sampled-data networked control systems[J]. IEEE Transactions on Control Systems Technology, 2012, 20(6): 1613-1621. |
| [10] | 孙连坤, 万振凯, 张桂玲. 具有随机通信逻辑的网络控制系统稳定性分析[J]. 控制与决策, 2010, 25(9): 1302-1306. Sun L K, Wan Z K, Zhang G L. Stability for networked control systems with stochastic communication logic[J]. Control and Decision, 2010, 25(9): 1302-1306. |
| [11] | Rehbinder H, Sanfridson M. Scheduling of a limited communication channel for optimal control[J]. Automatica, 2004, 40(3): 491-500. |
| [12] | Ishii H. H∞ control with limited communication and message losses[J]. Systems & Control Letters, 2008, 57(4): 322-331. |
| [13] | Zhang W A, Yu L, Feng G. Optimal linear estimation for networked systems with communication constraints[J]. Automatica, 2011, 47(9): 1992-2000. |
| [14] | Zhang L, Hristu-Varsakelis D. Communication and control co-design for networked control systems[J]. Automatica, 2006, 42(6): 953-958. |
| [15] | Hristu-Varsakelis D, Zhang L. LQG control of networked control systems with access constraints and delays[J]. International Journal of Control, 2008, 81(8): 1266-1280. |
| [16] | Guo G, Jin H. A switching system approach to actuator assignment with limited channels[J]. International Journal of Robust and Nonlinear Control, 2010, 20(12): 1407-1426. |
| [17] | 杜明莉, 周川, 陈庆伟, 等. 具有通信约束的网络控制系统动态调度与H∞控制协同设计[J]. 控制理论与应用, 2012, 29(9): 1132-1138. Du M L, Zhou C, Chen Q W, et al. Coordinate design of dynamic scheduling and H∞ control for networked control systems with communication constraints[J]. Control Theory & Applications, 2012, 29(9): 1132-1138. |
| [18] | Zhu C Q, Guo G. Optimal control for event-triggered networked control systems[J]. Control and Decision, 2014, 29(5): 802-807. |
| [20] | Schenato L, Sinopoli B, Franceschetti M, et al. Foundations of control and estimation over lossy networks[J]. Proceedings of the IEEE, 2007, 95(1): 163-187. |



