1 引言
经典控制理论在一定程度上能较方便地处理单变量控制系统的相关问题,但它所提供的方法有明显的凑试性,仅限于系统存在微小摄动的不确定性情况. 状态空间方法能较好地解决多变量控制系统的分析和综合问题[1, 2, 3, 4, 5, 6, 7],改善得到的LQG(linear quadratic Gaussian)状态反馈线性控制系统具有很好的稳定裕度. 然而以上两种方法对被控对象摄动的鲁棒性不够理想[8]. Zames[9]首次提出了利用控制系统内某些信号间的传递函数的H∞范数作为优化指标的设计思想. 随后,Doyle等[10]提出直接状态空间法,这是H∞控制理论的最大突破,他们将标准H∞控制问题归结为两个代数Riccati方程的求解问题.
Iwasaki等[11, 12]把H∞控制问题的求解进一步归结为线性矩阵不等式的求解,提出了广义KYP(GKYP)引理,从而将H∞控制问题转化为一个凸优化问题来处理. 在传统的z域法和状态空间法的基础上,Hara等[13]根据所设计的连续PID控制器的传递函数离散化得到了数字PID控制器,尽管得到的闭环控制系统能在采样时间取得较小时达到预期的性能指标,但随着采样时间的进一步减小,系统的所有极点向z平面稳定边界移动,反之随着采样时间的增大,阶跃响应的性能变差,甚至会出现系统振荡及不稳定的现象. Mochizuki等[14]针对板球系统利用GKYP引理提出了一种PID控制器设计方法. 文[15]提出了线性参数变化系统的一种新型控制器设计方法,基于GKYP引理设计了线性参数变化系统的降阶控制器,且干扰输入的谱信息可以由一个矩阵值积分二次约束标征. 最近,文[16]简要综述了KYP引理和GKYP引理的进展及应用. 然而,上述研究主要集中在线性连续系统的时域分析和控制器设计,且缺乏对系统鲁棒性分析,具有一定的局限性.
本文将GKYP引理应用于线性离散控制系统,根据系统频率和采样周期的乘积范围划分离散系统的z域,并利用模型匹配原则[17]将PID控制器的设计问题转化为求解相应区域内H∞范数构成不等式的最优解问题. 然后,将此不等式的求解问题转化为控制器和被控对象状态空间表达式各系数所组成线性矩阵不等式(linear matrix inequality,LMI)[18]的求解问题. 这种方法综合考虑了频率与采样周期的取值,使控制系统提高了对频率和采样周期取值的鲁棒性,使设计的数字PID控制器有更大的适用范围,在满足系统性能要求及确保系统稳定性的同时,使采样周期的取值范围变宽.
2 预备知识 2.1 近似模型匹配图 1所示为离散控制系统.
 |
| 图 1 离散控制系统结构图Fig. 1 Configuration chart of discrete-time control system |
图 1中,D(z)表示数字PID控制器; Kc(z)表示被控对象进行z变换后的传递函数. 根据模型匹配原则,先选择一个参考模型,其开环传递函数记作Kε(z). 这样就可以通过解以下不等式来完成对D(z)的设计:

其中,ε是给定的正实数. ε取值越小,模型匹配的效果越好[19].
2.2 GKYP引理对于矩阵Μ,其转置矩阵及共轭转置矩阵分别记作ΜT和Μ*. Μ是Hermitian矩阵,即满足Μ=Μ*. 对于矩阵Φ和P,它们的张量积记作Φ⊗P.
引理1[12] 给定复矩阵
 其中
其中 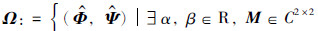 使得
使得 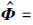

定义  假设(A,B)是可控的,且A不含特征值λ使得
假设(A,B)是可控的,且A不含特征值λ使得  成立. 那么以下陈述是等价的:
成立. 那么以下陈述是等价的:
1) 对于A的所有特征值λ∈Λ下述不等式成立
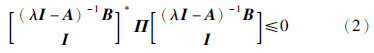
2) 存在Hermitian矩阵P和Q,满足Q>0,且

一个线性连续时间系统的状态空间表达式为

对其进行离散化处理,取采样周期为T,采样时间表示为kT(k=0,1,2,…). 设控制输入u(t)只在采样时刻发生变化,在相邻两采样时刻之间,u(t)是通过零阶保持器保持不变的,且等于前一采样时间之值,即在kT和(k+1)T之间,u(t)=u(kT)=常数,则式(4)离散化得到的状态空间表达式为

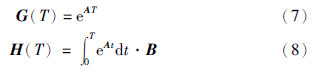
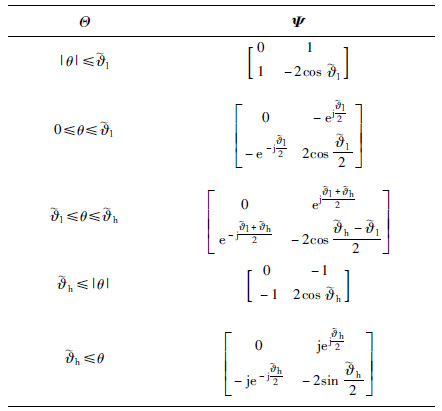
根据文[12]中按频域对Ψ进行划分的方法及z=esT=ejωT的转换关系,可得表 1.
为便于讨论,将Θ表示为
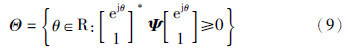


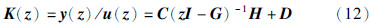
推论1 给定G∈Rn×n和H∈Rn×m(G和H可由连续系统中A和B唯一确定)以及Hermitian矩阵Π∈C(n+m)×(n+m),设K(ejθ)=(ejθI-G)-1H,当det(ejθI-G)≠0(∀θ∈Θ)时,下列条件等价:
1) ∀θ∈Θ,

2) 存在Hermitian矩阵P和Q,满足Q>0,且

证明 令ejθ=λ,则有ejθe-jθ-1=0,其等价的矩阵形式为  .
.
根据引理1可得  ,又由θ∈Θ,可知λ∈Λ. 进而,根据实矩阵的转置与共轭转置等价的事实,可得此推论成立.
,又由θ∈Θ,可知λ∈Λ. 进而,根据实矩阵的转置与共轭转置等价的事实,可得此推论成立.
推论2 给定G∈Rn×n和H∈Rn×m(G和H可由连续系统中A和B唯一确定)以及Hermitian矩阵Π∈C(n+m)×(n+m),设K(ejθ)=(ejθI-G)-1,则当det(ejθI-G)≠0(∀θ∈Θ)时,下列条件等价:
1) ∀θ∈Θ,

2) 存在Hermitian矩阵P和Q>0,且

证明 因为  为标量,所以有
为标量,所以有


令  则
则



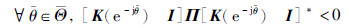

 . 根据推论1,推论2中1)成立的等价条件为: 存在Hermitian矩阵P和Q>0,使得式(16)成立,所以结论2)成立. 证毕.
. 根据推论1,推论2中1)成立的等价条件为: 存在Hermitian矩阵P和Q>0,使得式(16)成立,所以结论2)成立. 证毕.
由推论1可得以下定理:
定理1 当det(ejθI-G)≠0(∀θ∈Θ)时,不等式  成立的充要条件是存在Hermitian矩阵P和Q>0使得
成立的充要条件是存在Hermitian矩阵P和Q>0使得
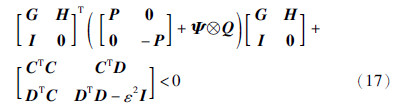
证明 根据H∞范数的定义,可得 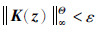 等价于
等价于  ,其中σmax为最大奇异值. 根据K(z)定义有
,其中σmax为最大奇异值. 根据K(z)定义有

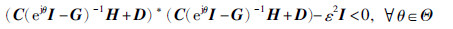
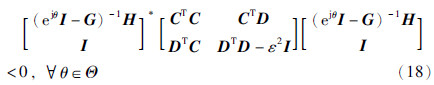
取 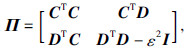 ,根据推论1,当det(ejθI-G)≠0(∀θ∈Θ)时,式(18)成立的充要条件是存在Hermitian矩阵P和Q>0使得式(17)成立,即此定理成立. 证毕.
,根据推论1,当det(ejθI-G)≠0(∀θ∈Θ)时,式(18)成立的充要条件是存在Hermitian矩阵P和Q>0使得式(17)成立,即此定理成立. 证毕.
定理1的对偶形式如定理2所示,定理2的形式在实际问题中应用范围更为广泛.
定理2 当det(ejθI-G)≠0(∀θ∈Θ)时,则不等式 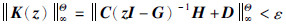 成立的充要条件是存在Hermitian矩阵P和Q>0使得下述不等式成立:
成立的充要条件是存在Hermitian矩阵P和Q>0使得下述不等式成立:

证明 类似于定理1的证明,根据无穷范数及奇异值的定义可得




定理3 当det(ejθI-G)≠0(∀θ∈Θ)时,则不等式 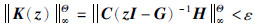 成立的充要条件是存在Hermitian矩阵P和Q>0使得下述不等式成立:
成立的充要条件是存在Hermitian矩阵P和Q>0使得下述不等式成立:


证明 由定理2知,当D=0时,不等式



因此,结合Schur补引理,便可得式(20),证毕.
4 数值仿真例 考虑连续线性控制系统被控对象:

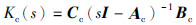 转化为状态空间形式可得
转化为状态空间形式可得

由式(12)可得Kc(z)=Cc(zI-Gc)-1Hc+Dc,其中Gc和Hc可由Ac和Bc求得.
我们的目的是设计数字PID控制器使得在单位阶跃输入下,输出响应没有静态误差; 且使最终串联上控制器的系统的超调量不大于30%,上升时间tr不大于0.5 s,调节时间ts不大于1 s; 系统频率变化及采样时间变大或变小时,系统具有一定鲁棒性,能保持其输出性能并且稳定.
在s域内PID控制器的传递函数可表示为


则z域内的PID控制器可表示为

根据系统性能指标的设计要求得到参考模型的传递函数为

记K(z)=D(z)Kc(z)-Kε(z)=C(zI-G)-1H,经推导得到G和H可表示如下:
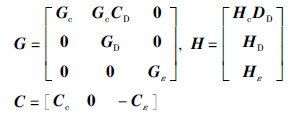
从而,可将不同频率及采样时间对应下的离散控制系统的PID控制器优化设计的问题转化为通过  计算状态空间表达式各项系数矩阵中不同参数的问题.
计算状态空间表达式各项系数矩阵中不同参数的问题.
对于被控对象Kc(s),其单位负反馈系统的阶跃响应曲线如图 2所示.
 |
| 图 2 原闭环系统阶跃响应曲线Fig. 2 Step response curve of the original closed loop system |
Iwasaki等[12, 13]提出的z域数字PID控制器设计是在计算出D(s)的基础上利用Tustin差分法将其离散化,即

基于该方法得出在不同采样时间下的阶跃响应曲线如图 3所示.
 |
| 图 3 基于式(21)控制器的阶跃响应曲线Fig. 3 Step response curves based on formula (21) controller |
当采样周期T较小时,这种方法还可达到预期的性能指标. 随着采样周期降低,最小相位系统的离散时间模型会变成具有不稳定零点的非最小相位系统,且极点向稳定边界移动; 反之,随着采样周期增大,由于此方法并没有考虑采样时间与原连续系统频率间的关系,即没有考虑其乘积所在的区间. 因此,阶跃响应的性能变差,甚至会出现系统振荡及不稳定的现象.
在给定误差限  及TD=0.001 s后,根据本实例所研究系统的频率取值及采样时间的取值范围,按表 1中格式可把角度划分为0≤θ≤0.2,θ≥0.2和|θ|≥1.5这3种情况,再应用本文方法设计PID控制器,只需将上述推导及数据代入定理3中不等式(20),进一步根据求得的
矩阵G和H可得控制器参数为: KP=0.31,KI=0.1,KD=0.04. 该控制器的设计方法综合考虑了ω,T,ωT的取值,这样使θ落在更为合适的区间,从而使得Ψ的取值更符合实际情况的需求. 只要选取合适的参考模型,就可提高控制系统性能,即提高控制系统对频率及采样时间的鲁棒性. 利用所设计的控制器作用于系统进行仿真,获得阶跃响应曲线如图 4所示. 由图 4可知,随着采样时间的增加,系统依然保持了良好性能,并未出现振荡及不稳定现象.
及TD=0.001 s后,根据本实例所研究系统的频率取值及采样时间的取值范围,按表 1中格式可把角度划分为0≤θ≤0.2,θ≥0.2和|θ|≥1.5这3种情况,再应用本文方法设计PID控制器,只需将上述推导及数据代入定理3中不等式(20),进一步根据求得的
矩阵G和H可得控制器参数为: KP=0.31,KI=0.1,KD=0.04. 该控制器的设计方法综合考虑了ω,T,ωT的取值,这样使θ落在更为合适的区间,从而使得Ψ的取值更符合实际情况的需求. 只要选取合适的参考模型,就可提高控制系统性能,即提高控制系统对频率及采样时间的鲁棒性. 利用所设计的控制器作用于系统进行仿真,获得阶跃响应曲线如图 4所示. 由图 4可知,随着采样时间的增加,系统依然保持了良好性能,并未出现振荡及不稳定现象.
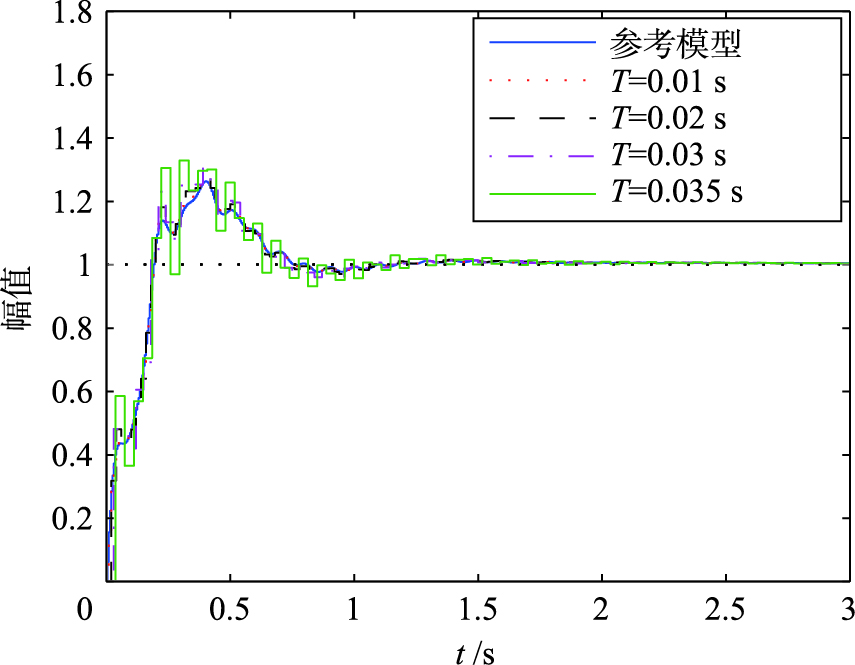 |
| 图 4 基于模型匹配PID控制器的阶跃响应曲线Fig. 4 Step response curves based on approximate model matching PID controller |
本文提出利用系统频率和采样周期划分z域来改进数字PID控制器的设计方法,结合GKYP引理、 H∞范数和模型匹配原则,提出了频域下控制器设计和解线性矩阵不等式之间的等价关系. 该方法减小了采样周期对系统性能的影响,从而提高了控制系统的鲁棒性,所设计的数字PID控制器也具有更广的应用范围.
| [1] | 李大字, 焦军胜, 靳其兵. 基于对角关联矩阵的广义多变量控制系统性能评价[J]. 信息与控制, 2013, 42(2): 157-161. Li D Z, Jiao J S, Jin Q B. Performance assessment of generalized multivariable control systems based on diagonal interactors[J]. Information and Control, 2013, 42(2): 157-161. |
| [2] | Al-Hadithi B M, Jiménez A, López R G. Fuzzy optimal control using generalized Takagi-Sugeno model for multivariable nonlinear systems[J]. Applied Soft Computing, 2015, 30: 205-213. |
| [3] | Zhang R D, Gao F R. An improved decoupling structure based state space MPC design with improved performance[J]. Systems & Control Letters, 2015, 75: 77-83. |
| [4] | Paduart J, Schoukens J, Pintelon R. Nonlinear state space modelling of multivariable systems[C]//2005 International Symposium on Nonlinear Theory and its Applications (NOLTA2005), Bruges, Belgium, 2005: 614-617. |
| [5] | Mercère G, Bako L. Parameterization and identification of multivariable state-space systems: A canonical approach[J]. Automatica, 2011, 47(8): 1547-1555. |
| [6] | 乔俊飞, 王莉莉, 韩红桂. 基于ESN的污水处理多变量自适应预测控制[J]. 信息与控制, 2014, 43(3): 368-373, 380. Qiao J F, Wang L L, Han H G. Multivariable adaptive predictive control for wastewater treatment process based on ESN[J]. Information and Control, 2014, 43(3): 368-373, 380. |
| [7] | 郭伟, 王汉杰, 夏友亮, 等. 基于状态空间方程的多变量PID-MAC在锅炉燃烧控制系统中的应用[J]. 热力发电, 2014, 43(9): 48-53, 59. Guo W, Wang H J, Xia Y L, et al. Application of state space equation based multivariable PID-MAC in boiler combustion control system[J]. Thermal Power Generation, 2014, 43(9): 48-53, 59. |
| [8] | 褚健, 俞立, 苏宏业. 鲁棒控制理论及应用[M]. 杭州: 浙江大学出版社, 2000. Chu J, Yu L, Su H Y. The theory and application of robust control[M]. Hangzhou: Zhejiang University Press, 2000. |
| [9] | Zames G. Feedback and optimal sensitivity: Model reference transformations, multiplicative seminorms and approximation inverses [J]. IEEE Transactions on Automatic Control, 1981, 26(2): 301-320. |
| [10] | Doyle J C, Glover K, Khargonekar P P, et al. State-space solutions to standard H2 and H∞ control problems[J]. IEEE Transactions on Automatic Control, 1989, 34(8): 831-847. |
| [11] | Iwasaki T, Hara S. Generalized KYP lemma: Unified frequency domain inequalities with design applications[J]. IEEE Transactions on Automatic Control, 2005, 50(1): 41-59. |
| [12] | Iwasaki T, Hara S. Generalization of Kalman-Yakubovic-Popov lemma for restricted frequency inequalities[C]//Proceedings of the 2003 American Control Conference. Piscataway, NJ, USA: IEEE, 2003: 3828-3833. |
| [13] | Hara S, Iwasaki T, Shiokata D. Robust PID control using generalized KYP synthesis: Direct open-loop shaping in multiple frequency ranges[J]. IEEE Control Systems, 2006, 26(1): 80-91. |
| [14] | Mochizuki S, Ichihara H. Generalized Kalman-Yakubovich-Popov lemma based I-PD controller design for ball and plate system[J]. Journal of Applied Mathematics, 2013, 854631, 1-9. |
| [15] | Sun G H, Ge D M, Wang S J. Induced L2 norm control for LPV system with specified class of disturbance inputs[J]. Journal of the Franklin Institute, 2013, 350(2): 331-346. |
| [16] | Iwasaki T. Generalized KYP lemma and applications[J]. Encyclopedia of Systems and Control, 2014, 1-7. |
| [17] | Dehghani A, Lanzon A, Anderson B D O. A two-degree-of-freedom H∞ control design method for robust model matching[J]. International Journal of Robust and Nonlinear Control, 2006, 16(10): 467-483. |
| [18] | 惠俊军, 张合新, 周鑫, 等. 含非线性扰动的区间变时滞系统鲁棒稳定新判据[J]. 信息与控制, 2014, 43(5): 529-533. Hui J J, Zhang H X, Zhou X, et al. New robust stability criteria for interval time-varying delay systems with nonlinear perturbations[J]. Information and Control, 2014, 43(5): 529-533. |
| [19] | Dehghani A, Lanzon A, Anderson B D O. An H∞ model referencing design utilizing a two degree of freedom controller scheme [C]//The 44th IEEE Conference on Decision and Control and 2005 European Control Conference. Piscataway, NJ, USA: IEEE, 2005: 2302-2307. |