1 引言
随着风力发电大型化的发展,减小机组本身不平衡载荷[1]显得尤为重要. 传统的统一变桨距控制方法(collection pitch control,CPC)没有考虑风剪切效应、 湍流效应和塔影效应等因素对风轮的影响,随着风轮半径的不断加大,风切效应对风机的影响越来越大. 因此,独立变桨距控制(individual pitch control,IPC)成为目前各国风电控制研究的热点. 独立变桨控制策略能较好地应对不平衡的气动载荷对风机产生的不良影响,使风机桨叶的受力更稳定均衡,从而安全稳定地控制风机运行[2].
国内针对独立变桨距控制技术的研究工作起步较晚,而统一变桨距技术已日趋成熟. 统一变桨距技术的研究针对统一变桨距机组的控制特点以及风能的多变性因素,主要着力于恒功率控制过程中的功率波动问题. 传统的前馈模糊PI(proportional-integral)复合变桨距控制、 LQG(linear quadratic Gaussian)控制、 准滑模变结构控制和RBF(radial basis function)神经网络控制等策略在统一变桨距控制技术中的应用对于独立变桨距控制技术的研发具有一定的参考价值[3, 4, 5, 6, 7, 8].
目前,对于风电机组独立变桨距中桨距角控制,多数使用传统的PI控制器及其复合控制[13]、 模糊PID控制、 LQG控制器[9, 10, 11, 12]等. 风能具有随机性和不稳定性的特点以及实际运行过程中还会遇到风切变、 塔影效应、 湍流和阵风等情况,加之风力发电机组的特性会随着时间和空间发生变化,往往使得传统的控制系统偏离设计时所依据的标称特性[13],因而难以达到较好的控制性能和稳定性.
模糊权系数独立变桨距控制[13]具有实现简单和可靠运行的特点,而支持向量机(support vector machine,SVM)是一种依据统计学习理论和结构风险最小化原理的新型学习机[14]. 与神经网络相比,支持向量机方法,可以有效地解决有限样本条件下的高维数据模型构建问题,并具有泛化能力强、 收敛到全局最优和维数不敏感等优点[15]. 本文将支持向量机和权系数控制相结合,提出一种基于在线支持向量机学习的权系数的独立变桨距学习控制方案,在实现功率稳定输出的同时,可以对参数在线适时调整,并进一步减小不平衡载荷干扰机组的恶劣影响,延长机组寿命.
2 风力发电系统建模 2.1 风力机数学模型风力发电系统风轮将风能转化为风机动能是一个复杂的气动力过程. 为了表示风轮在不同风速中的状态,用叶片的叶尖圆周速与风速之比来衡量,称为叶尖速比λ:
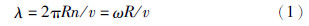
风力机的捕捉功率可表示为
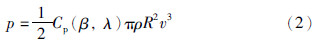
式中: ρ为空气的密度; Cp为风能利用系数; β为叶片的桨距角; Cp(β,λ)为叶尖速比和桨叶节距角的函数.
叶片上的载荷包括空气动力载荷、 重力载荷、 惯性载荷、 操纵载荷和其他载荷等.
作用在叶片上的空气动力载荷包括摆振方向剪力Qyb和弯矩Mxb、 挥舞方向(轴向)剪力Qxb和弯矩Myb以及变桨距时与变桨距平衡的叶片俯仰力矩Mzb,如图 1所示.
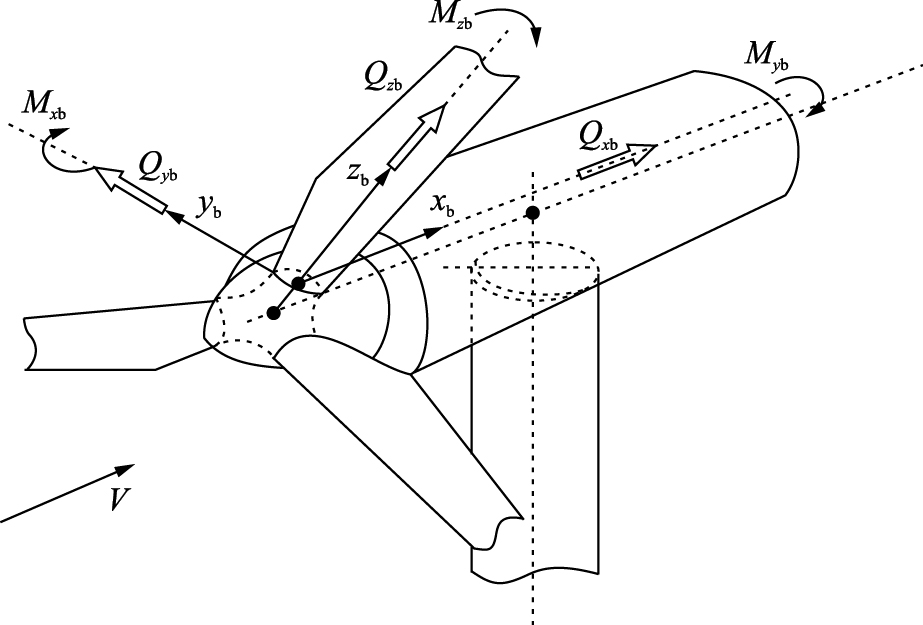 |
| 图 1 叶片坐标系Fig. 1 Blade coordinate system |
由图 1及分析叶素受力可知,作用在叶素上的法向力dFn和切向力dFt为
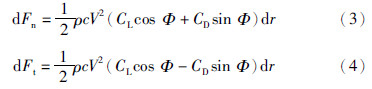
利用积分的方法即可计算得到作用在风轮上的旋转驱动力矩Ta、 轴向力Fa、 倾斜力矩Mt和偏转力Fg:
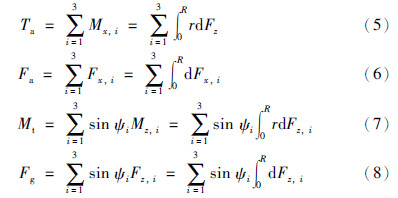
假设发电机d轴和q轴的电感相等,直驱式永磁同步发电机的电磁转矩表达式为

由于采用直驱永磁风电系统的风力机和发电机无需经增速齿轮箱而直接联接. 假设在整个变速范围内有恒定的机械传动效率,并对结构特性进行一些简化假设,传动系统的动态模型可以用一个一阶运动方程表示:
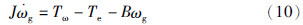
变桨的灵敏度与精确度对功率输出影响很大. 变桨距执行机构通过液压装置或电机驱动系统实现,可以等效为一个一阶惯性环节:

基于SVM模糊权系数独立变桨距控制系统框图如图 2所示. 控制策略分为2个部分,第一部分是功率控制器,采用模糊控制器对系统进行控制,以得到系统的统一桨距角给定值. 第二部分是SVM权系数独立变桨距控制器,包括权系数分配单元、 SVM优化补偿和权系数调整运算单元. 权系数分配单元得到优化设计的权系数. SVM优化补偿将叶片方位角和桨叶轴向气动力结合后形成SVM模糊权系数控制器的训练样本进行训练,SVM权系数控制器通过支持向量机学习算法对样本数据按照目标函数进行离线学习得到控制器的结构和初步参数. 然后进行在线学习校正. 权系数调整运算单元根据前两部分的输出探索需要合成独立变桨控制输出.
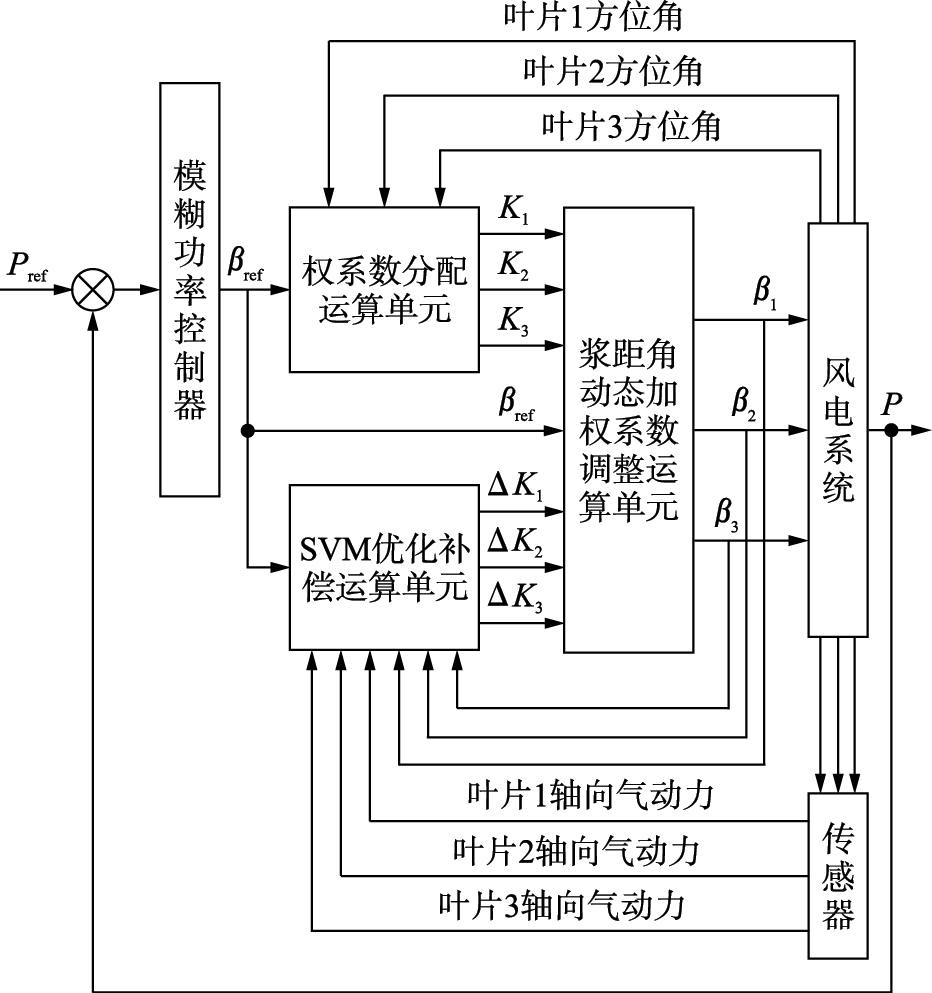 |
| 图 2 SVM模糊权系数独立变桨距控制系统Fig. 2 The individual pitch control system based on SVM fuzzy weight coefficient |
根据风资源模型,每个叶片受到的平均风速为
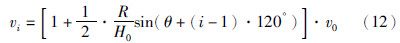

根据支持向量机的原理,支持向量机获取知识只能从样本中学习得到,因此学习样本的数量和质量是影响支持向量机学习效果和学习速度的重要因素. 设给定训练样本为(x1,y1),…,(xn,yn),xi∈Rn,yi∈Rn,n为数据的总数. 对于线性回归,考虑用线性回归函数式(14)估计数据.
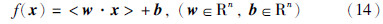
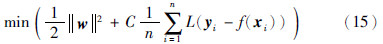
约束条件: | yi-f(xi)≤ε|.
其中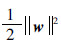 称作正则化风险,它控制模型的复杂度;
称作正则化风险,它控制模型的复杂度; 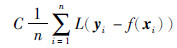 称作经验风险,参数C称为正则化参数.
称作经验风险,参数C称为正则化参数.
回归函数f(x)形式上类似于一个神经网络,如图 3所示. 输出是中间节点的线性组合,它与传统径向基函数RBF方法的基本区别是其每一个基函数的中心对应一个支持向量,这些支持向量以及输出权值都是由结构风险最小化算法自动确定的.
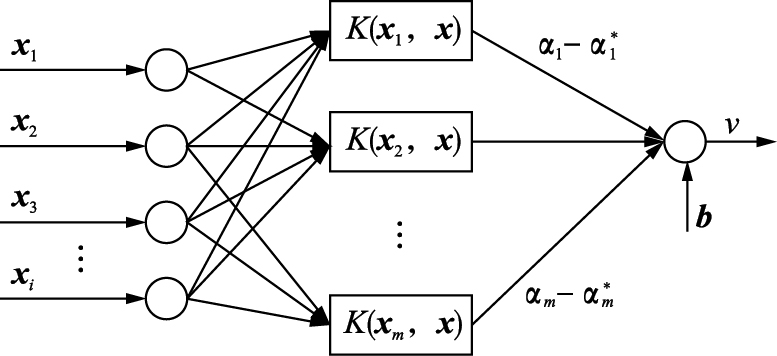 |
| 图 3 支持向量机补偿Fig. 3 Support vector machine compensation |
取径向基函数(RBF)核:
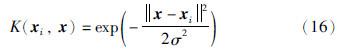
其中: 中心为支持向量,σ为高斯核函数的宽度.
3.3.2 离线学习离线学习阶段采用模型数据批量学习得到的变桨距控制器的初步参数和结构,保证在控制初期就可以满足系统控制品质的要求,减轻控制器在线学习的负担.
3.3.3 在线学习
由于风力发电系统处在不断变化的环境中,所以采用在线学习的方法实现对环境的不断自适应. 采用增量式在线学习算法[16],并以KKT(Karush-Kuhn-Tucker)条件为基础,当有新样本加入时,通过修改拉格朗日乘子和偏置值来更新SVM变桨控制器的结构和参数. 在线学习算法实现部分主要包括递增算法和递减算法. 根据KKT条件和拉格朗日乘子把训练的样本数据分成3个子集: 错误支持向量集: E={i=(|θi|=C,|h(xi)|≥ε)},边界支持向量集: B={i=(0<|θi|
训练目标是将新样本(xc,yc)加入上述3个集合之一,同时使所有样本仍满足KKT条件. 核函数K(xi,x)为满足Mercer定理的任意对称正定函数,不需要知道非线性变换的具体形式,就可用核函数来实现算法线性化.
主要控制目标就是通过调整拉格朗日乘子α和修改偏置项b来确保新增加的样本都满足KKT条件. 为提高函数逼近性能,增量式在线SVM模糊权系数独立变桨距控制实现过程如下:
Step 1: 获取新的数据样本(Fic,βic);
Step 2: 根据设定的评估周期判断数据是否有效,若有效则加入训练样本集; 否则丢弃数据转Step 1;
Step 3: 根据KKT条件和拉格朗日乘子,得到边界支持向量集B、 错误支持向量集E和保留样本集R;
Step 4: 计算SVM优化补偿单元输出Δβi;
Step 5: 计算以Δβi输出为均值、 按正态分布用于探索的扰动值;
Step 6: 以功率控制器、 权系数单元和SVM补偿单元输入得到的动态加权系数控制值作为桨距角参考值,对变桨距对象进行控制;
Step 7: 使用递减算法,删除训练集中所需要遗忘的样本,得到新的支持向量集BD、 错误支持向量集ED和保留样本集RD;
Step 8: 等待数据在线更新,转Step 1.
递减部分: 从训练集D删除样本时,在保持其它训练样本的KKT条件不变的前提下,调整要去除样本的对应参数αc. 递增算法与递减算法类似,只是过程相反.
上述算法有选择性地将新数据加入到支持向量机训练集,通过对每次迭代过程中增加的样本进行学习,在线调整SVM模糊权系数控制器参数,实现系统的不断优化. 在线学习方法能利用前面运算的结果,在保证在线支持向量非线性逼近能力的基础上,降低在线训练过程的计算量. 这样不但能缩短其训练时间,而且能提高控制器的自适应性.
3.4 在线学习算法训练数据的获取训练样本的质量决定了学习得到的SVM模糊权系数补偿器参数的优劣,期望训练样本既能反映被控对象在控制过程中的变化规律,又能使系统具有良好的响应特性. 从稳定功率输出和减轻机械负荷两方面定义判定有效学习数据的阈值条件:
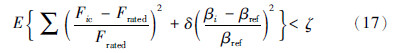
为验证上述独立变桨距控制策略的正确性和合理性,本文在加拿大Opal-RT公司RT-LAB实时仿真系统上,对1台2 MW直驱永磁同步风电机组进行独立变桨距控制系统仿真研究,并对SVM模糊权系数独立变桨距控制策略和模糊权系数独立变桨距控制策略进行比较,机组主要参数见表 1.
| 风轮半径/m | 桨叶数 | 风轮转动惯量/(kg·m2) | 电机转动惯量/(kg·m2) | 额定功率/MW | 定子电阻/Ω | d、 q轴电感/H | 定子额定电压/V |
| 40 | 3 | 411 183 | 18 904.7 | 2 | Ra=6.7e-3 | Ld=Lq=2.7 | 660 |
| 电机极对数 | 额定轴转矩/(kN·m) | 发电机额定转速/(r/m) | 发电机最大转速/(r/m) | 额定风速/(m/s) | 切入切出风速/(m/s) | 空气密度/(kg/m3) | |
| 30 | 940 | 9~22.5 | 29 | 14 | 3, 25 | 1.29 | |
风速是风电系统主要的外部信号,并决定风电系统的运行状态. 仿真中采用阶跃风和丹麦Ris国家实验室建立的基于凯马(Kaimal)频谱的随机风速模型,如图 4所示,随机风基本风速为14 m/s,湍流强度为12%.
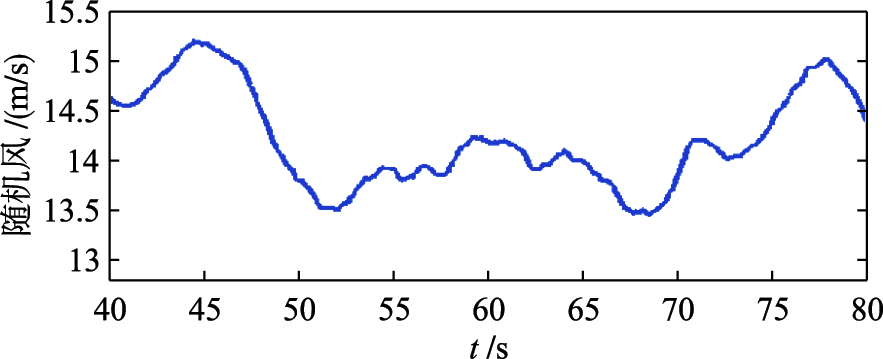 |
| 图 4 基本速度为14 m/s的随机风曲线Fig. 4 Radom wind curve with mean speed 14 m/s |
由图 5和图 6可知,基于支持向量机权系数的独立变桨距控制在阵风之后具有更快的响应速度,功率波动程度也明显减小. 同时,桨距角的变化幅值也相比权系数独立变桨距控制没有那么大,说明SVM权系数控制器不断地对新样本实时进行学习,在线校正控制器参数,随着时间的推移,控制器拟合效果越来越好,最后实现优化输出功率的目的.
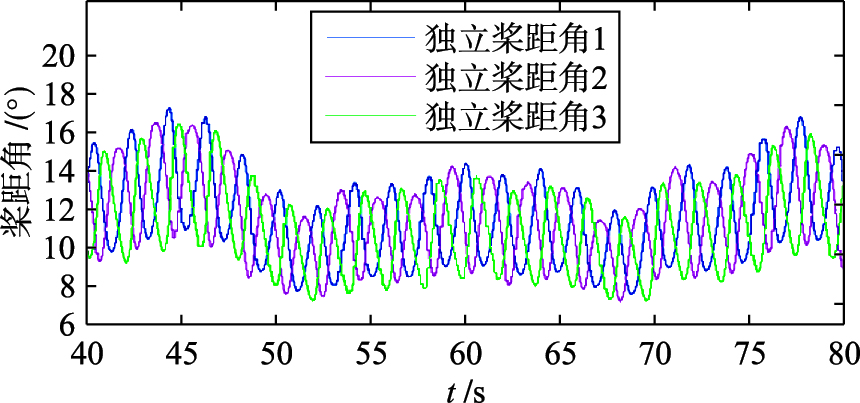 |
| 图 5 权系数桨距角变化曲线Fig. 5 Curves of pitch angle based on weight coefficient |
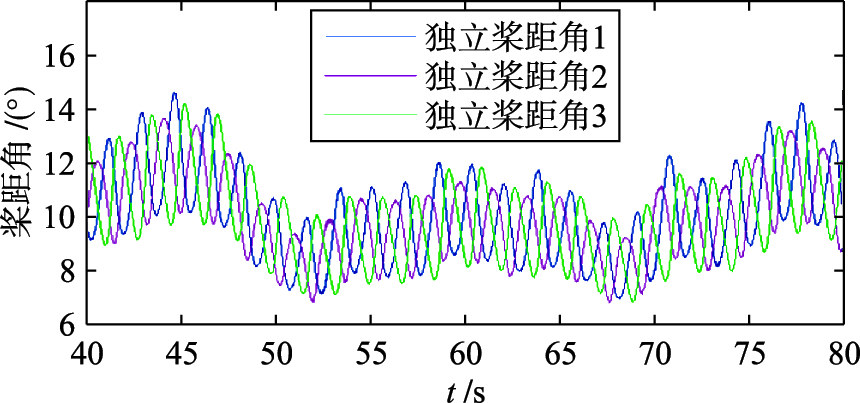 |
| 图 6 SVM权系数桨距角变化曲线Fig. 6 Curves of pitch angle based on SVM weight coefficient |
由图 7可知,基于支持向量机模糊权系数独立变桨距控制下的功率输出相对权系数独立变桨距能更快地平滑到额定功率附近,输出没有出现较高的频率振荡,具有较好的抑制功率波动的效果. 由于SVM模糊权系数控制器前期是采集样本学习并对学习样本进行有效性判断,使得功率输出的波动幅值变化不大. 利用在线学习机制,随着时间的增加,控制器精度会不断增强,稳态后功率波动较小,表现出更好的稳定性.
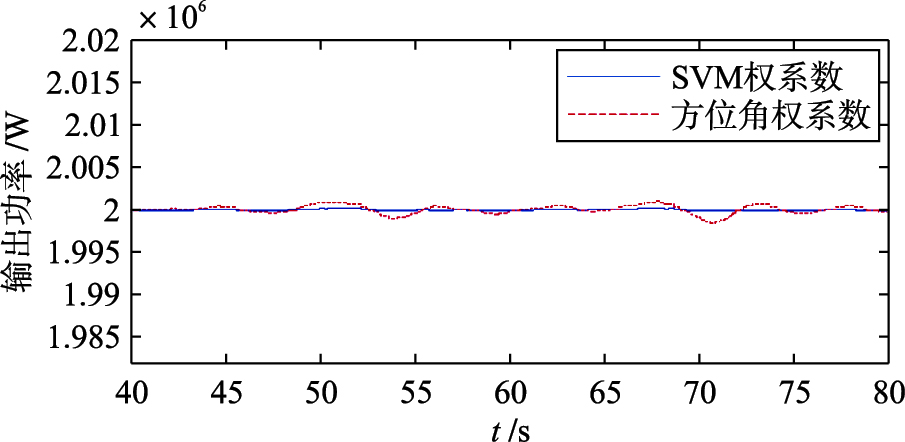 |
| 图 7 输出功率曲线Fig. 7 Curves of the out power |
由图 8可知,在SVM权系数独立变桨距控制下,风力机的轮毂载荷明显减小,并且载荷波动限制在±3.2%之内,小于权系数独立变桨距控制下的±7.7%,故能更好地抑制不平衡载荷的波动情况,表明SVM在解决非线性问题上表现出更好的控制特性. 因此,基于SVM权系数独立变桨距控制在减轻单个叶片疲劳载荷的同时,大大改善了整个机组载荷波动,使风电机组能够正常安全稳定地运行,保证对电能质量的要求.
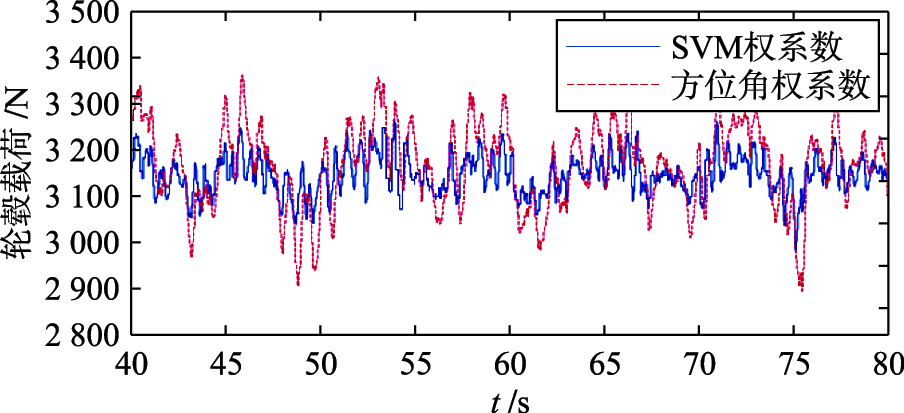 |
| 图 8 轮毂载荷曲线Fig. 8 Curves of wheel load |
本文针对永磁直驱风力发电系统的独立变桨距控制问题,设计了基于支持向量机模糊权系数独立变桨距控制器. 通过对控制器的输入输出映射得到控制器初步参数和结构,在此基础上利用在线支持向量机算法实现控制器自学习功能. 然后构建永磁直驱风力发电系统独立变桨距控制系统模型并在RT-LAB实时仿真系统上进行仿真. 仿真结果表明,在随机风速条件下,该控制策略不仅能满足输出功率稳定和减少不平衡载荷的要求,而且具有较好的控制快速性和强鲁棒性,同时又能实时校正模型参数而未产生频繁的动作,从而满足控制器更高的精度要求,延长桨叶寿命,达到较好的控制效果. 因此这对风力发电系统中难以精确建模和运行过程中外部扰动强烈的控制问题具有重要意义.
| [1] | 戴巨川, 胡燕平, 刘德顺, 等. 大型风电机组变桨距载荷计算与特性分析[J]. 中国科学: 技术科学, 2010, 40(7): 778-785. Dai J C, Hu Y P, Liu D S, et al. Calculation and characteristics analysis of blade pitch loads for large scale wind turbines[J]. Science China: Technological Sciences, 2010, 40(7): 778-785. |
| [2] | 叶杭冶. 风力发电机组的控制技术[M]. 北京: 机械工业出版社, 2007. Ye H Z. Control strategies of wind turbine generators[M]. Beijing: China Machine Press, 2007. |
| [3] | Jelavic M, Petrovic V, Peric N. Individual pitch control of wind turbine based on loads estimation[C]//34th Annual Conference of IEEE Industrial Electronics Society. Piscataway, NJ, USA: IEEE, 2008: 228-234. |
| [4] | 高峰, 徐大平, 吕跃刚. 大型风力发电机组的前馈模糊PI变桨距控制[J]. 动力工程, 2008, 28(4): 537-542, 588. Gao F, Xu D P, Lu Y G. Feed forward fuzzy-PI pitch-control for large-scale wind turbines[J]. Chinese Journal of Power Engineering, 2008, 28(4): 537-542, 588. |
| [5] | Prats M A M, Carraseo J M, Galvan E, et al. Improving transition between power optimization and power limitation of variable speed, variable pitch wind turbines using fuzzy control[C]//26th Annual Conference of the IEEE Industrial Electronics Society. Piscataway, NJ, USA: IEEE, 2000: 1497-1502. |
| [6] | 姚兴佳, 张雅楠, 郭庆鼎. 大型风电机组三维模糊控制器设计与仿真[J]. 中国电机工程学报, 2009, 29(26): 122-127. Yao X J, Zhang Y N, Guo Q D. Design and simulation of the three-dimensional fuzzy controller for large wind turbine[J]. Proceedings of the CSEE, 2009, 29(26): 122-127. |
| [7] | 张雷, 李海东, 李建林, 等. 基于LQR方法的风电机组变桨距控制的动态建模与仿真分析[J]. 太阳能学报, 2008, 29(7): 781-785. Zhang L, Li H D, Li J L, et al. Dynamic modeling and simulation of pitch control strategy for wind turbines based on LQR method[J]. Acta Energiae Solaris Sinica, 2008, 29(7): 781-785. |
| [8] | 秦斌, 周浩, 杜康, 等. 基于RBF网络的风电机组变桨距滑模控制[J]. 电工技术学报, 2013, 28(5): 37-41. Qin B, Zhou H, Du K, et al. Sliding mode control of pitch angle based on RBF neural-network[J]. Transactions of China Electrotechnical Society, 2013, 28(5): 37-41. |
| [9] | 林勇刚, 李伟, 陈晓波, 等. 大型风力发电机组独立桨叶控制系统[J]. 太阳能学报, 2005, 26(6): 780-786. Lin Y G, Li W, Chen X B, et al. The research on large scale wind turbine individual blade pitch control system[J]. Acta Energiae Solaris Sinica, 2005, 26(6): 780-786. [ZK)] |
| [10] | Lu X P, Gu H G, Ling Y G, et al. Research on the load control of wind turbines based on Individual pitch technology[J]. Acta Energiae Solaris Sinica, 2011, 32(11): 1591-1598. |
| [11] | Yao X J, Liu Y, Guo Q D. A control method for split range individual pitch based on feed-forward azimuth angle weight number assignment[J]. Acta Energiae Solaris Sinica, 2011, 33(4): 532-539. |
| [14] | Zheng X X, Qian F. An SVM-based on-line modeling method and its application[J]. Information and Control, 2005, 34(5): 636-640. |
| [16] | Parrella F. Online support vector regression[D]. Genoa, Italy: University of Genoa, 2007. |



