2. 交通运输部水运科学研究院, 北京 100088
2. China Waterborne Transport Research Institute, Beijing 100088, China
1 引言
目前,随着跨海大桥、 钻井平台等海上大型工程的繁荣发展,海上实施土木工程建设的需求越来越广,无动力土建设施的运输量也越来越大,这些无动力设施由于自身没有任何动力,需要依靠船舶拖带辅助其海上浮运. 这些无动力目标设施往往需要配置多艘拖船才可以保证其运输的可靠性,拖带船舶之间的协调主要依靠人工操纵,在调整时需要清楚每一艘拖带船舶的状况,不仅要考虑单艘拖带船舶的操纵影响,还要协调其它拖带船舶的操纵,使之整体配合拖运目标的运动. 造成整个拖带系统的操纵时间加长、 速度变慢很大程度是受人为因素影响,而自适应能力弱也相应地增大了拖带的风险概率. 如果任何一艘拖船不能及时配合或者出现差错,就有可能导致无动力设施的倾覆或沉没,很难挽救,会造成巨大损失.
近年来,无人驾驶智能船舶的研发逐渐成熟,智能控制技术已应用于航海领域,对于拖带系统的拖航控制方面,重点偏重于拖航稳定性的研究,周正同[1]讨论无舵驳船拖航时横摇加速度对拖航安全的影响,给出无舵驳船提高稳定性的方法,使用风筝式拖尾巴解决,林大钦[2]对拖航中偏荡问题进行分析,并提出应对措施,上述两者都是针对拖带轨迹中的偏移问题,从实际操纵方面给出建议,并没有改善拖航控制方面出现的问题. Jiang[3]使用三自由度操纵模型结合状态方程仿真拖船上的PID(proportion integration differentiation)自动舵的动力响应过程,讨论拖航参数对系统稳定效应的影响,Fitriadhy[4]通过建立缆绳运动方程得到拖带时的系统轨迹变化状况,但没有考虑拖带船舶和被拖船舶之间的关联影响,周江华在文[5]中考虑了此联系,通过找出拖船与被拖船航向偏差之间的关联,设计采用非线性控制器,使得被拖船横向运动限制在一个很小的范围,从而保证拖航的稳定性,这种思路目前并没有太多的研究.
综上所述,国内外大都是研究拖带操纵运动模式以及运动轨迹稳定性,关于拖航控制方面,还只是关注拖带船舶的单船控制,而对于整体系统来说,没有过多关注,大多是一些人工如何操纵方面的描述,很多涉及拖带系统中拖船间如何相互智能控制,本文针对拖带系统研究拖船间的智能协调方式,使得无动力目标拖带系统通过某种控制技术,可以自动地带动系统运动,并且拖带船舶之间可以根据目标的移动轨迹智能调节各自的运动,使得目标可以保证稳定的浮运路线.
2 协同控制策略分析协同学是复杂性科学的代表理论之一,探讨整个复杂系统最终形成的总体模式,它由赫尔曼·哈肯[6]在20世纪70年代首次提出,协同即协调合作,可以看作在普遍规律支配下的有序的、 自组织的集体行为. 赫尔曼·哈肯从序参数和支配角度研究协同作用,支配原理调动着整体的运动,整体中各个部分的行为影响着序参数的变化,对于拖带系统,支配原理是指控制系统转向运动的总体策略,序参数是指拖带船舶和被拖目标个体的影响参数. 利用协同学思想,进行拖带系统间的协同控制.
文中以两个拖带船舶拖带无动力被拖目标组成的拖带系统为研究对象,重点研究拖带系统在协同控制策略下的智能转向,使之自动运动到指定的转向航向方位上,在运动过程中,既要保证3个个体的航向达到转向航向,又要减少拖带中被拖目标的左右偏移和震荡,尽量保持平稳转向.
由于被拖目标是无动力控制的,它影响着整个拖带系统的转向运动,拖船与被拖目标之间受到缆绳的牵引,对其施加不同力度和方向的拖力控制着运动轨迹,同时拖船船位的变化,会影响着缆绳拖力和航向角之间的变化,因此,选取拖船拖力和转向角度两大因素联合控制,构建协同策略,进而支配拖带船舶和被拖目标的相互运动,达到稳定转向的目的.
由图 1可得,两个拖船的运动轨迹通过拖力协同控制之后影响着无动力目标的运动轨迹,侧拖拖船的航向经过航向协同控制后影响着运动轨迹,因此,拖船和被拖目标的船位决定着协调控制策略,针对它们设计协调控制算法,通过拖带系统的位置变化趋势控制着拖力和航向角,进而调整整个系统的变化轨迹,达到智能协调的目的.
 |
| 图 1 拖带系统构造Fig. 1 Towing system construction |
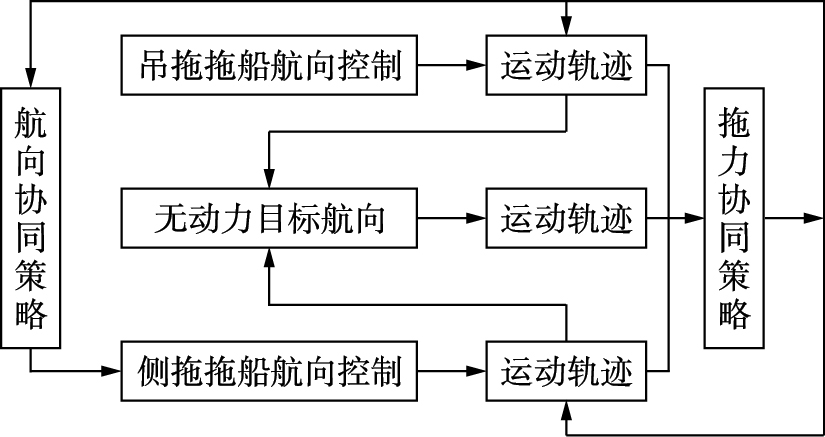 |
| 图 2 协同控制策略结构Fig. 2 Structure of coordinated control strategy |
图 1所示的拖带系统中,吊拖拖船主要是向前牵引无动力目标,侧拖拖船主要用来辅助无动力目标的转向,无动力目标在两个拖船的拖带下进行浮运,当系统转向时吊拖拖船首先进行转向,通过缆绳带动着无动力目标运动,由于拖带物体没有动力,会造成一定幅度的横向偏移,而侧拖拖船用来减少这种横向震荡,辅助无动力目标尽快地到达转向角度.
图 3所示,虚线位置表示无动力目标的理想位置,实际中必然会产生图中dp标识的横向偏移,而且在转向过程中,会产生一定的波动,根据第2节的协同策略中可控因素有航向角和拖力两个方面,通过智能协调这两个方面,调整拖船和被拖目标的船位,使之减少偏移影响,到达稳定转向目的.
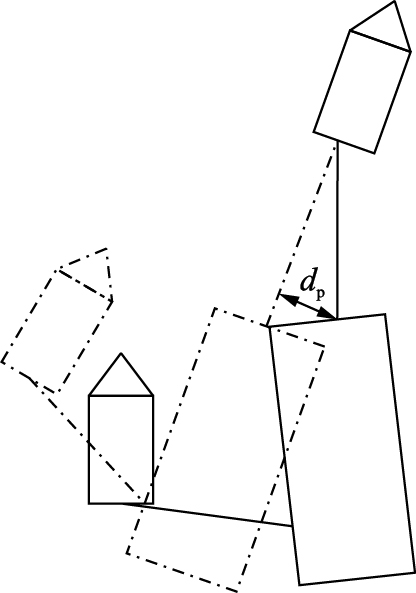 |
| 图 3 拖带系统转向示意图Fig. 3 Steering schematic diagram of towing system |
根据第2节所述,系统的协同控制与船位信息紧密相关,现根据图 3所示的转向系统,构建拖带的船位模型[7, 8, 9, 10, 11].
根据图 4中信息,有如下等式:
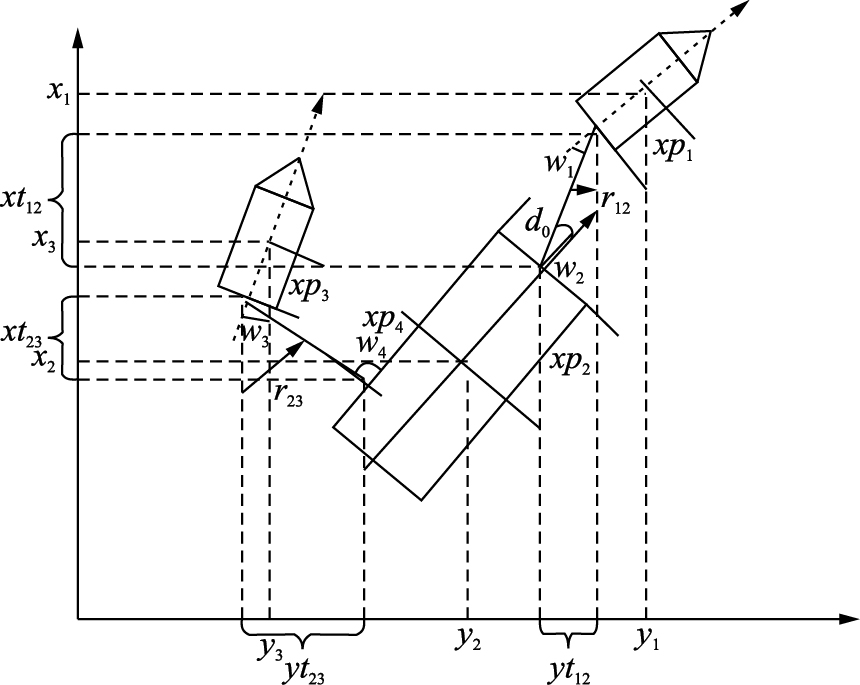 |
| 图 4 拖带系统船位信息Fig. 4 Towing system position information |

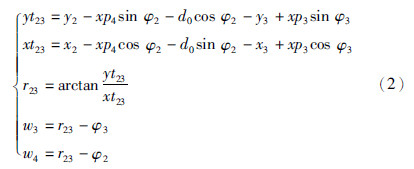
式(1)、式 (2)分别描述了拖带系统中船舶位置和航向之间的变化影响,考虑了缆绳之间的耦合关联,得出了缆绳的长度和角度变化趋势,是进行协同调控的前提和条件.
3.2 航向角协同控制在航向控制中,吊拖拖船起主导作用,按照设定的转向角度值进行转向,而系统间通过缆绳的耦合关系,得出合适的转向幅度,赋予侧拖拖船,使其航向随着吊拖拖船的航向协同变化,将原来独立的两个拖船航向变化关联起来,实现智能调控.
当无动力目标产生横向偏移dp时,对应着航向与缆绳的夹角w1(见图 4),关系如下:


在系统转向调控下,此时侧拖拖船的转向航向即为r12,结合2.1节的船位模型,r12的值由吊拖拖船与无动力目标的船位信息决定,可根据式(1)求解.
因此,给定系统转向角度φd时,吊拖拖船以φd值进行转向,在缆绳牵引作用下,造成系统的船位变化,进而根据船位变化,控制侧拖拖船的转向角度,形成航向角的协同控制. 当转向结束系统稳定时,无动力目标逼近理想状态,r12值逼近φ1值,系统中的整体航向趋势趋于φd.
3.3 拖力协同控制当航向角控制系统姿态时,系统间主要通过缆绳力传递变化,缆绳力强度受到拖船提供的拖力影响,在系统转向过程中,拖船船位和被拖目标的位置不断改变,会影响拖带时所需拖力大小,在实际操纵时,可以通过调整车钟,改变主机转速,进而改变提供拖力的大小.
在智能控制中,需要自行判断何时改变拖力大小,以及改变程度.
由于拖带系统是3个个体所组成,可将它看做一个群,使用群集概念,在群中个体与个体之间的相对运动,以及群整体在外界环境中的宏观运动,都来源于周边“势场”中的吸引和排斥,这里的势场可以是数学意义上的虚拟力场——人工势能函数[12, 13],个体之间可以互相作用,使得整个群体形成一个固定的网络拓扑.
群内部人工势场函数Vij,是一个关于距离rij的非负、 可微、 无界的函数,rij=ri-rj,并满足以下条件:
(1) 当||rij||→0时,Vij(||rij||)→∞.
(2) 当个体i与个体j之间的距离||rij||达到一定值时, Vij存在最小值.
根据定义构造如下势场函数[14]:
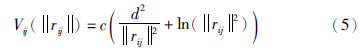
其中,||rij||是两个相邻个体间的距离,c>0为增益系数,d是预先设定的两个相邻个体间的平衡距离,在||rij||=d处势场函数取得最小值,当相邻个体之间距离大于d时,它们会相互吸引,反之,相互排斥. 因此,群体中个体的聚集及分离行为可通过上述势场函数进行调节. 引斥力可用势场力表示[15, 16]:
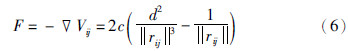
人工势能函数的思想常常运用于队形控制、 编队跟踪[17, 18]中,然而在拖带系统中,个体之间使用缆绳进行连接,船舶之间也不需要精准定位跟踪,考虑到系统间船位关系影响到拖力的调整,所以,可以利用势能力思想辅助判断拖船和被拖目标之间的聚集和分离.
借助人工势能法,系统在转向时,个体船位的变化引发系统间势能力引斥的变化,以图 3中系统的理想状态为参照,设定平衡距离d,当个体之间距离保持平衡时,不受任何势场力影响,不需要调整,一旦脱离平衡,个体间受到引或斥力的影响,使得所需拖力大小发生变化. 在拖力协同控制中,主要是吊拖拖船与无动力目标、 侧拖拖船与无动力目标之间力的调配,通过计算它们之间船位距离,代入式(6)中,得出势场力的正负,当F<0时,为引力,拖力应变大,F>0时为斥力,拖力应变小,然而考虑到系统间转动惯量大、 滞延性等特点,还需加强判断拖力调整的条件,利用2.1节中缆绳与航向夹角的变化角度进行趋势判断.
对于吊拖拖船与无动力目标之间,当图 4中的|w1|偏离一定幅度,且其变化趋势增大时,即满足|w1|>θ,dw1>0时,如果体现为引力则拖力上调,反之下降. 对于侧拖拖船与无动力目标之间,当图 4中的|w1|偏离一定幅度,且w3变化趋势增大时,即满足w1>θ,dw3>0时,如果此时体现为引力则拖力上调,反之下降.
因此,通过拖力之间的调控,使得系统间个体尽可能地减少相互偏移,维持在稳定的幅度内,平稳过渡,快速完成转向目标.
3.4 稳定性验证对于水面船舶,其定常状态为匀速直线航行,当系统转向后其航向转变,重心轨迹最终恢复为一条直线,称之为直线运动稳定性[7, 8, 19, 20],即
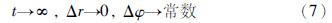
拖带系统中无动力目标的航向和轨迹受到吊、 侧拖拖轮的影响,在转向过程中进行协同控制策略调整,关注无动力目标航向变化.
MMG(mathematical model group)模型公式:
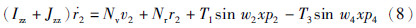
由式(1)、 式(2)、 式(4)得到

将式(9)代入式(8)中,随着时间增加,进入转向结束状态,此时φ3→φ2,w1、 w2、 w3、 w4状态趋于固定,则sin w2→0,Nvv2-T3sin w4xp4近似为常数,这里用M表示,由于  ,可将式(8)转化为
,可将式(8)转化为
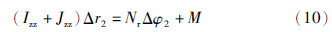
当进入转向结束状态时,协同控制调整完毕,拖船不再对无动力目标进行调整,Δr2→0,根据式(10)得到Δφ2→常数,满足式(7)稳定条件,因此,系统在协同控制转向后可以达到稳定状态.
4 仿真验证 4.1 协同控制技术运用船舶MMG模型进行运动建模,将无动力目标看成无动力的MMG模型,结合2.1节的船位模型得到拖带系统运动趋势,并对吊拖和侧拖拖船进行协同控制. 吊拖拖船航向直接采用PID控制,设定转向角度30°,侧拖拖船航向按照式(4)进行航向协同控制,此时航向控制律为
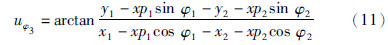
根据式(6)由拖船和无动力目标间距离判断势能力,进而调节两个拖船的拖力. 参照实际拖船情况,设置全速、 半速、 慢速、 微速4个车钟档,则吊拖和侧拖拖船拖力变化律为


初始车钟档设在半速档上,假设每个档上对应的缆绳受力固定,依据式(12)进行拖力调控.
拖船和无动力目标参数信息见表 1、 表 2.
| 船长/m | 船宽/m | 型深/m | 吃水/m | 方形系数 | 排水量/t | 最大系柱拖力/t |
| 60.22 | 11.6 | 5.7 | 4.16 | 0.51 | 1 472 | 20 |
使用Matlab的Simulink平台实施模型搭建进行仿真测试. 在转向过程中,利用协同控制技术,在不考虑风浪干扰情况下,得到运动轨迹如图 5所示.
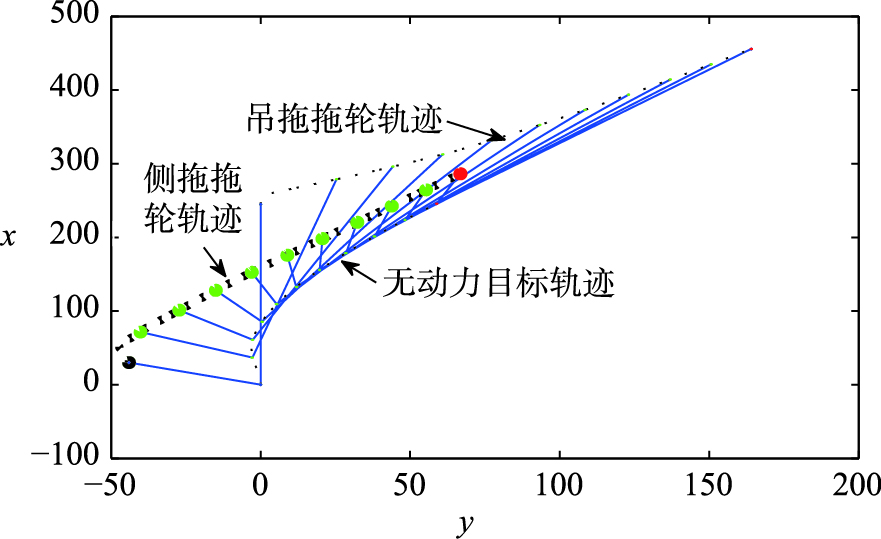 |
| 图 5 拖带系统轨迹图Fig. 5 Towing system track diagram |
图 5是按图 3所示系统得出的转向轨迹,以船舶重心位置为轨迹采样点,在轨迹图中选取一定采样间隔并加上缆绳以作显示. 由整体趋势可以看出,初期航向变化有波动不稳定,随着航向转变慢慢趋于设定航向,侧拖船舶与无动力目标间的距离逐渐缩短,转向后期系统轨迹趋势渐渐平缓,实现转向目标.
图 6是未加协同控制和加上控制之后的无动力目标航向变化趋势,可以看出未加调控的航行浮动趋势明显,加上调控之后航向幅度变化平缓,基本呈上升趋势. 图 7是未加协同控制和加上控制之后的吊拖拖船缆绳与其航向之间夹角幅度变化,对比得出调控后的目标偏离幅度减小,趋势变缓,降低了系统的震荡程度,因此协调控制技术在一定程度上改善了拖带系统的运动品质.
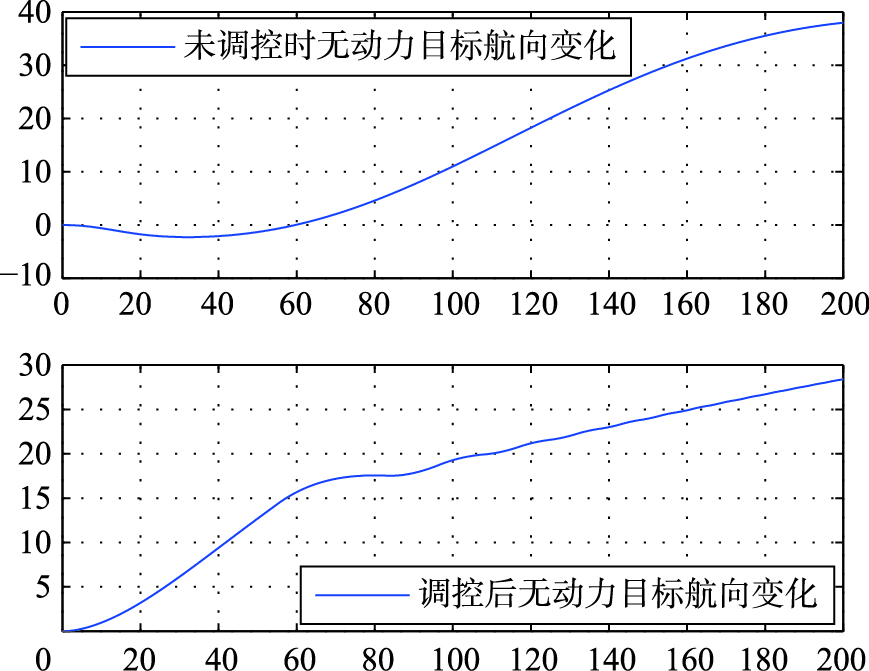 |
| 图 6 航向变化趋势比较Fig. 6 Course changing trend |
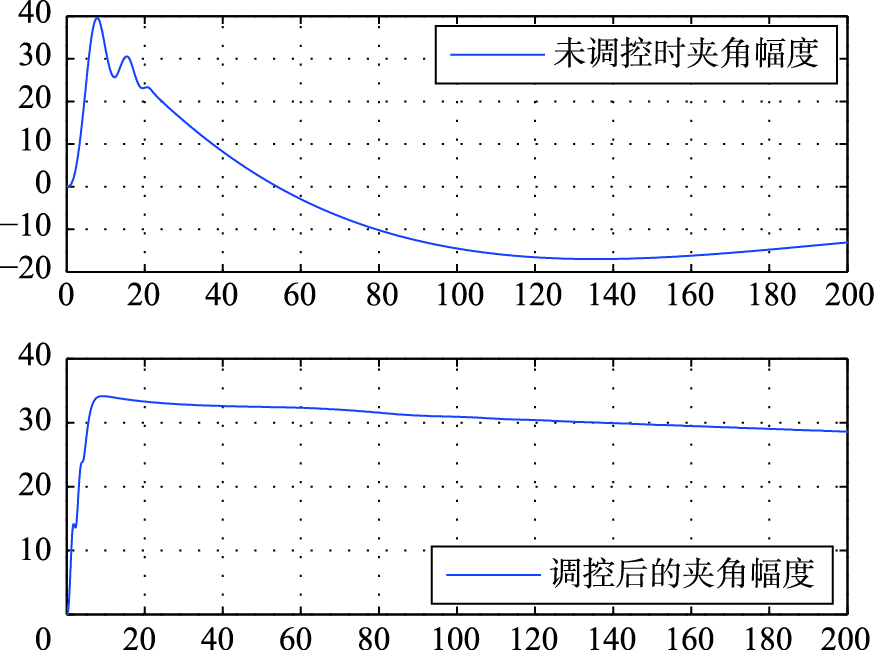 |
| 图 7 夹角变化趋势比较Fig. 7 Angle changing trend |
图 8分别显示的是无动力目标和侧拖拖船的航向变化,由图可知,无动力目标受到两个拖船影响航向变化较大,随机性较强,在控制过程中,部分时段超过了设定的转向航向,后来经过控制调整后逐渐接近于设定航向,此时转向结束,慢慢到达稳定趋势,侧拖拖船航向受到系统角度变化影响,协同控制后逐渐趋于转向目标,到后期与无动力目标都达到航向稳定.
 |
| 图 8 航向协同控制趋势Fig. 8 Course coordinated control trend |
图 9所示的是吊拖拖船缆绳与其航向之间夹角w1的趋势,转向初始阶段无动力目标惯性大,控制滞缓,致使角度变化较大,随着调控作用,大小慢慢减小,最终接近于零度,逼近理想状态.
 |
| 图 9 夹角变化趋势Fig. 9 Angle changing trend |
仿真时要对缆绳受力长度做出限制,当缆绳长度超过设定上限时发生断缆,当短于设定下限时虽保持连接,但是缆绳呈不受力状态拖力此时为0. 图 10中上、 下图分别是吊拖拖船和无动力目标之间缆绳长度与侧拖拖船和无动力目标之间缆绳长度的变化,没有出现断缆的情况,仍在一定缆绳受力范围内,总体变化趋势为减小,到最后维持在设定的下限周边小幅度浮动,几乎不再变化,意味着系统转向达到稳定,转向过程结束,接下来开始系统的直航,需要进行新的调控.
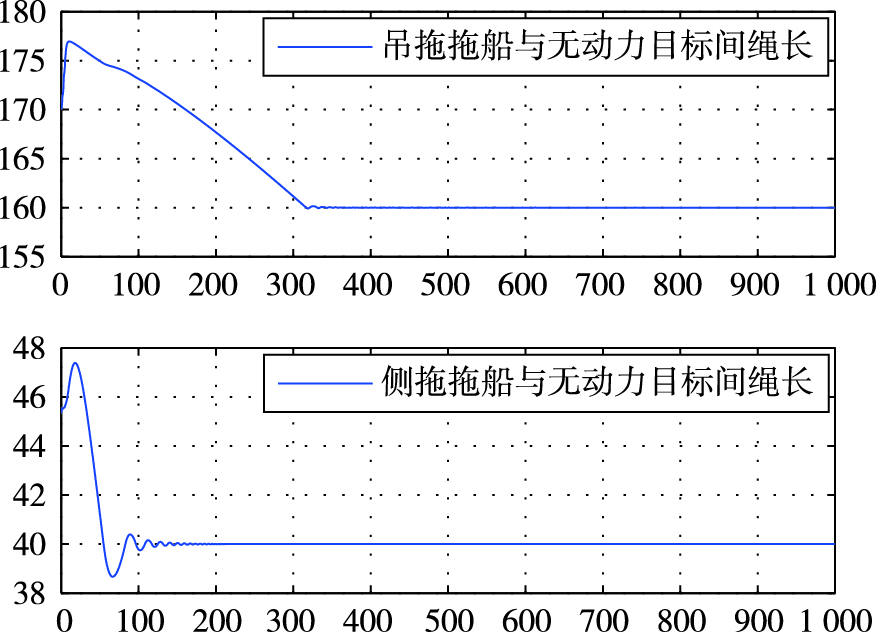 |
| 图 10 缆绳变化趋势Fig. 10 Rope changing trend |
图 11显示转向过程中吊拖、 侧拖拖船对无动力目标的拖力变化,结合图 10来看,仿真初期,绳长变化在设定范围内,两个拖力都按照判断策略进行调整,后期绳长到达边界时,拖力在0边界往复波动,这主要是由于仿真中设置的绳长限制影响,而此时系统已经基本完成转向目标,逐渐进入新的直航状态,需重新设计调控策略以符合直航要求,在此文中没有涉及到此阶段,因此到转向完成后期会出现拖力频繁波动状况.
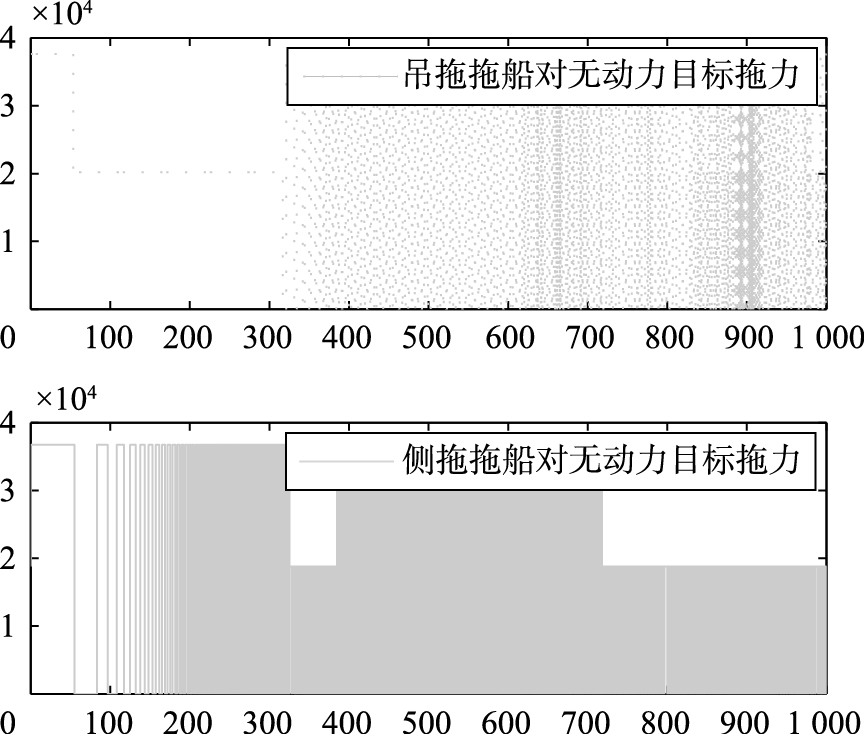 |
| 图 11 拖力协同控制趋势Fig. 11 Drag coordinated control trend |
综上所述,系统经过协同控制转向后可以达到稳定的状态,由于系统间个体是由柔性物质缆绳所连接,在转向时绳长不断变化,具有随机性,会影响受力状况,而整个系统仍能保持稳定性.
5 结论针对拖带系统的控制首次提出了智能协同控制策略,通过系统间的关联自发地调节航向和拖力大小,进而实现智能转向,得到了良好的效果,有一定的应用前景. 文中忽略了缆绳的形变对施加拖力产生的影响,假定受力固定,而且对只含有两个拖船的系统进行了研究,今后可以对更复杂的情况以及更多配置的拖船进行探索.
| [1] | 周正同. 无舵驳船拖航稳性及稳定性[J]. 江苏船舶, 2003, 20(4): 5-7. Zhou Z T. Without rudder barge towing stability and stability[J]. Jiangsu Ship, 2003, 20(4): 5-7. |
| [2] | 林大钦. 拖航中偏荡分析及其应对措施[C]//北京, 海洋出版社: 第五届中国国际救捞论坛论文集: 82-86. Lin D Q. Towing the yawing analysis and its countermeasures[C]//The Fifth China International Salvages BBS. Beijing, China Ocean Press: 82-86. |
| [3] | Jiang T, Sharma S D. Stabilization and control of the dynamic behavior of a tug tanker tow[J]. Ocean Engineering, 2008(34): 135-145. |
| [4] | Fitriadhy A, Yasukawa H, Koh K K. Course stability of a ship towing system in wind[J]. Ocean Engineering, 2013(64): 135-145. |
| [5] | 周江华. 采用非线性舵控制的海上船舶拖带稳定性和安全性动态模拟[J]. 华东船舶工业学院学报, 2005, 19(3): 25-27. Zhou J H. Using nonlinear rudder control sea ship towing stability and safety of dynamic simulation[J]. Journal of East China Shipbuilding Institute, 2005, 12(3): 25-27. |
| [6] | 赫尔曼·哈肯. 凌复华, 译. 协同学大自然构成的奥秘[M]. 上海: 上海译文出版社, 2013. Herman H. Ling F H, trans. Synergetic constitute the mysteries of nature[M]. Shanghai: Shanghai Translation Press, 2013. |
| [7] | 赵鹏举. 船舶拖航仿真研究[D]. 哈尔滨: 哈尔滨工程大学, 2008. Zhao P J. Ship towing simulation study[D]. Harbin: Harbin Engineering University, 2008. |
| [8] | 梁康乐. 拖航系统操纵性研究[D]. 上海: 上海交通大学, 2007. Liang K L. Towing system maneuverability research[D]. Shanghai: Shanghai Jiaotong University, 2007. |
| [9] | 李强. 拖航的运动建模与仿真[D]. 大连: 大连海事大学, 2009. Li Q. The modeling and simulation of the movement of the towage[D]. Dalian: Dalian Maritime University, 2009. |
| [10] | Milgram J H. Extreme tensions in open ocean towing[J]. Journal of Ship Research, 1995, 39(4): 328-346. |
| [11] | Yoshiyuki N, Yasukawa H, Hirata N. Time domain simulation of wave-induced motions of a towed ship in head seas[J]. Journal of the Japan Society of Naval Architects and Ocean Engineers, 2013, 15(1): 91-100. |
| [12] | 魏然. 基于人工势场理论的多移动机器人的协同控制研究[D]. 武汉: 华中科技大学, 2007. Wei R. Based on the theory of the artificial potential field about the coordinated control of multiple mobile robots research[D]. Wuhan: Huazhong University of Science and Technology, 2007. |
| [13] | 杨永明, 田彦涛, 陶军, 等. 基于社会势场的群体机器人聚集队形控制[J]. 系统仿真学报, 2009, 21(4): 1106-1110. Yang Y M, Tian Y T, Tao J, et al. Swarm robots aggregation formation control based on social potential fields[J]. Journal of System Simulation, 2009, 21(4): 1106-1110. |
| [14] | 俞辉. 多智能体机器人协调控制研究及稳定性分析[D]. 武汉: 华中科技大学, 2007. Yu H. Multi-agent robot coordinated control study and stability analysis[D]. Wuhan: Huazhong University of Science and Technology, 2007. |
| [15] | Ren W, Beard R W. Consensu seeking in multiagent systems under dynamically changing interaction topologies[J]. IEEE Transactions on Automatic Control, 2005, 50(5): 655-661. |
| [16] | Nakazawa K, Takahashi K, Kaneko M. Movement control of accompanying robot based on artificial potential field adapted to dynamic environments[J]. IEEE Transactions on Electronics, Information and Systems, 2014, 134(2): 293-302. |
| [17] | Ghommem J, Mnif F, Poisson G, et al. Nonlinear formation control of a group of underactuated ships[C]//Proceedings of the OCEANS 2007. Piscataway, NJ, USA: IEEE, 2007: 1-8. |
| [18] | 秦宇翔, 李一平, 徐红丽. 基于人工势场和模糊规则的多水下机器人队形控制方法[J]. 计算机测量与控制, 2012, 20(8): 2105-2107. Qin Y X, Li Y P, Xu H L. Based on artificial potential field and fuzzy rules of underwater robot formation control method[J]. Computer Measurement and Control, 2012, 20(8): 2105-2107. |
| [19] | Fang M C, Lin Y H, Kao Y C. Applying the optimized PD controller to the towing system in waves[J]. Journal of Taiwan Society of Naval Architects and Marine Engineers, 2014, 33(3): 135-144. |
| [20] | Fitriadhy A, Yasukawa H, Koh K K. Turning ability of a ship towing system[J]. Ship Technology Research, 2011, 58(2): 112-124. |



