1 引言
永磁同步电机(permanent magnet synchronous motor,PMSM)在许多重要领域得到了广泛应用,但在电压源逆变器驱动的PMSM控制系统中采用逆变器是容易出现故障的环节. 因此,为了提高控制系统的可靠性,对逆变器进行容错控制具有重要意义. 许多不同的逆变器容错方法已被提出[1],其中将三相六开关逆变器切换为三相四开关逆变器的容错方案由于具有易操纵、 结构简单和低成本等特点,可对单相开路或短路故障进行容错,逐渐成为逆变器容错研究的热点[2, 3, 4, 5, 6, 7, 8]. 已有研究者对三相四开关逆变器在矢量控制或直接转矩控制系统中的控制进行了研究[2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14].
在四开关逆变器控制中,由于电容分压的不均衡现象导致驱动系统的控制性能降低,在文[14]中详细介绍了出现电容电压不平衡现象的原因. 如何改善电容电压不平衡带来的不利影响成了四开关逆变器控制需要解决的问题之一.
近年来,由于模型预测控制(model predictive control,MPC)具有动态响应快、 易实现、 在线滚动优化和固有的鲁棒性等控制优点越来越受到研究者的重视[15, 16, 17, 18, 19, 20]. 其中基于磁链和转矩控制的模型预测转矩控制(model predictive toque control,MPTC)是将MPC应用到交流电机控制的成功案例,MPTC通过PMSM数学模型预测下一时刻的转矩和磁链,并进一步通过对目标函数的评估选取逆变器开关状态,从而控制电机.
为了利用MPTC对转矩和磁链快速、 灵活控制的特点,以及三相四开关逆变器容错方案的优点,本文在考虑电容分压不平衡因素下,对不平衡电压进行抑制,应用模型预测转矩控制策略对基于三相四开关逆变器的PMSM驱动系统进行控制.
2 容错逆变器拓扑及数学模型 2.1 四开关容错逆变器PMSM拓扑容错逆变器供电的PMSM系统结构如图 1所示,母线间两个串联电容的中点通过3个双向晶闸管TRn(n=a,b,c)分别连接到绕组输入端. 要实现逆变器的容错控制,根据对应的故障开关位置,断开熔断丝Fi(i=1,2,3),隔离故障桥臂,触发相应的双向晶闸管导通,故障桥臂将由串联电容取代.
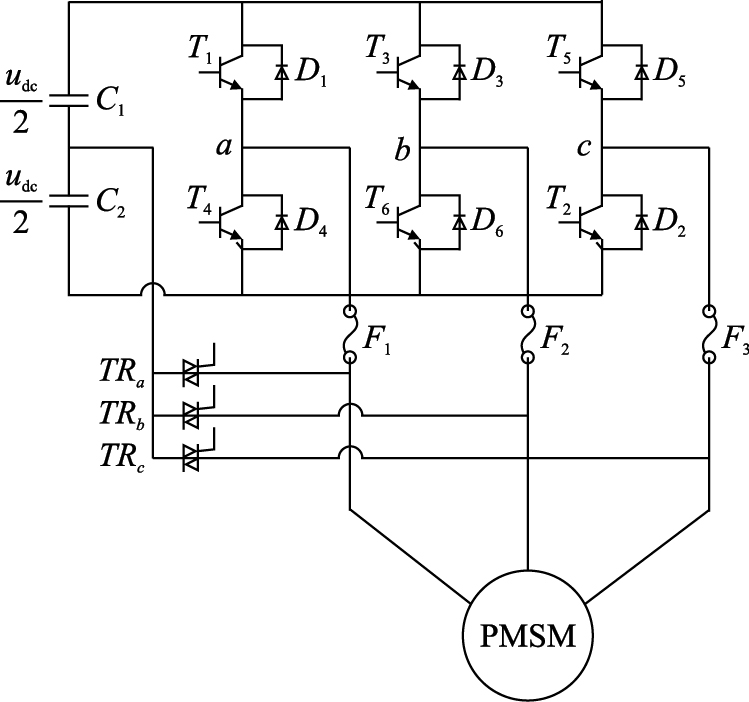 |
| 图 1 容错拓扑Fig. 1 Fault-tolerant topology |
不失一般性,本文以a相桥臂容错为例,此时四开关容错逆变器和电机的等效结构如图 2所示.
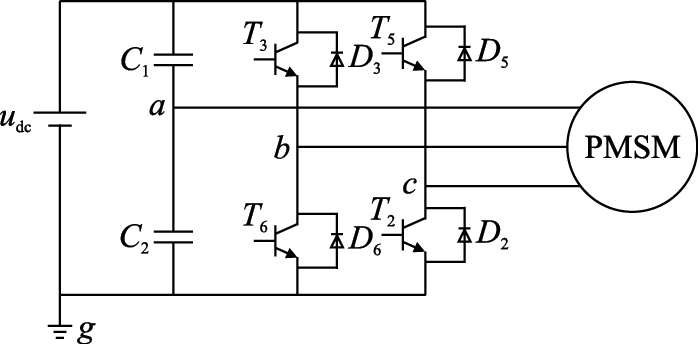 |
| 图 2 容错逆变器和电机的等效结构图Fig. 2 Equivalent structure of fault-tolerant inverter and motor |
在三相静止abc坐标系下可以列出连续时间永磁同步电机数学模型,三相电流方程表达式为
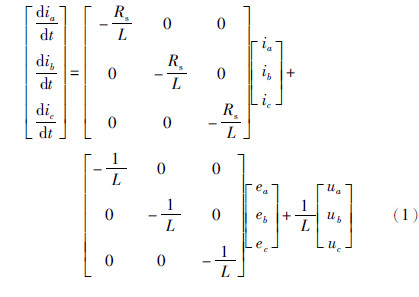
定子绕组各相电压为
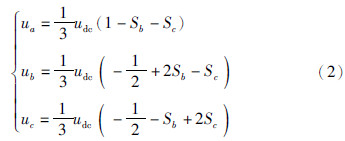
αβ坐标系下的定子磁链表达式为
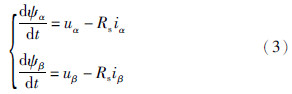
定子磁链的幅值方程为

永磁同步电机在二相静止αβ坐标系下的电磁转矩方程为
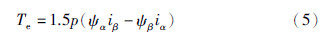
式(2)给出的绕组电压方程是在假设母线电容C1、C2电压平衡的基础上提出的. 对于三相四开关逆变器的控制,在实际系统中存在着电容电压的不平衡现象,即电容两端的电压将随着流过的电流产生波动.
由文[21]可知,假设不平衡电压为Δu,且C1=C2=C,则母线电容C1、 C2端电压为
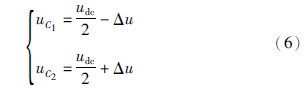
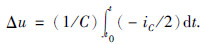
此时,定子绕组的各相电压为
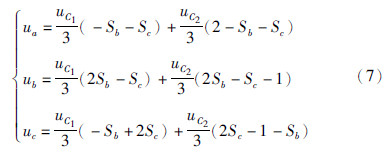
MPTC和直接转矩控制(direct torque control,DTC)都要选择电压矢量,但是选择电压矢量的方法有所不同,DTC通过预测值和给定值之间的差值从开关表中选择矢量; MPTC的基本思想是基于系统的模型来预测状态变量将来时刻的变化,通过评估定义的目标函数来选择相应的电压矢量. 由文[22]可知,MPTC在继承DTC快速动态响应的基础上,比DTC具有更小的转矩脉动. 本文所采用的MPTC由3部分组成: 预测模型,磁链、 转矩估计,目标函数最小化,整个控制系统结构如图 3所示.
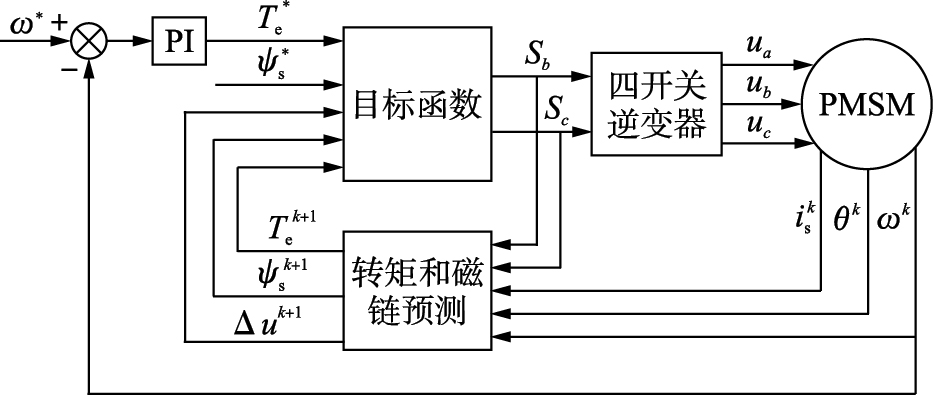 |
| 图 3 四开关容错逆变器控制系统Fig. 3 Four-switch fault-tolerant inverter control system |
根据离散化式(1)可得三相定子电流在下一时刻的预测值表达式:

通过离散化方程(3)可得k+1时刻αβ坐标系下的定子磁链表达式为
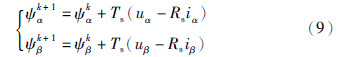
则k+1时刻定子磁链的幅值和电磁转矩方程为
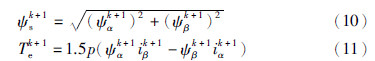
通过式(10)和式(11)可得定子磁链和电磁转矩的预测值.
目标函数通常根据控制目标来定义,为使电磁转矩和磁链收敛到给定值附近,同时抑制母线电容的不平衡电压,本文在MPTC中所定义的目标函数如下:
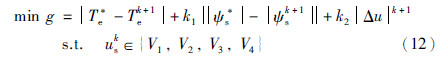
在数字控制系统中,由于控制策略的执行过程占用了一定的时间,导致在k时刻选择的电压矢量无法直接应用到k+1时刻,从而造成延时. 而延时将会对模型预测控制器性能造成较大的影响,因此为了消除延时对数字系统带来的不利影响,需对延时进行补偿. 因此,本文重新选取目标函数如下:
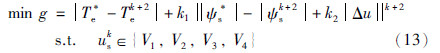
MPTC控制流程如图 4所示.
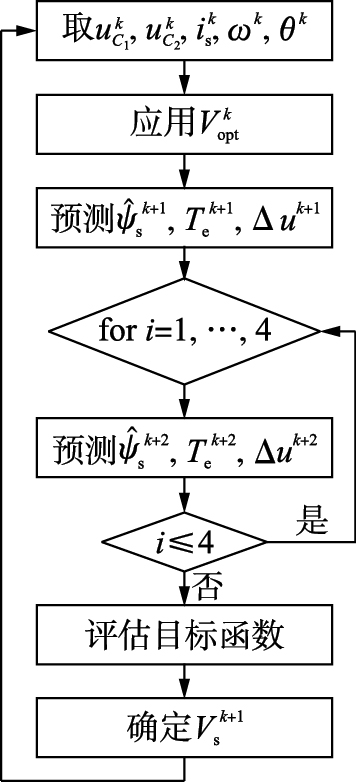 |
| 图 4 MPTC控制过程原理Fig. 4 Principle of MPTC control process |
为验证所提出的三相四开关容错逆变器模型预测转矩控制的正确性,利用Matlab/Simulink建立控制系统的仿真模型,驱动系统参数设置如表 1所示. 系统采样周期为10 μs,权重因子kl取值为33,k2取值为55,控制系统中的PI控制器参数设置为kp=0.1,ki=0.1. 在模型预测转矩控制下PMSM驱动系统带载启动.
| 符号 | 物理量 | 数据 |
| Rs | 定子电阻 | 2.875 Ω |
| L | 绕组电感 | 0.008 5 H |
| ψf | 永磁磁链 | 0.175 Wb |
| Bm | 摩擦系数 | 0 |
| J | 转动惯量 | 0.000 8 kg·m2 |
| T | 额定转矩 | 1.05 N·m |
| uc | 直流电源 | 350 V |
| ψ*s | 参考磁链 | 0.175 Wb |
| C | 母线电容 | 2 040 μF |
为验证采用不平衡电压抑制策略对系统性能的改善程度,将未采用抑制策略控制系统(系统1)和采用抑制策略控制系统(系统2)的输出响应曲线进行对比,图 5和图 6分别为系统1和系统2的转速响应图,图 7和图 8分别为其电磁转矩响应曲线,图 9和图 10分别为其三相定子电流响应. 图 11和图 12分别为其定子磁链响应.
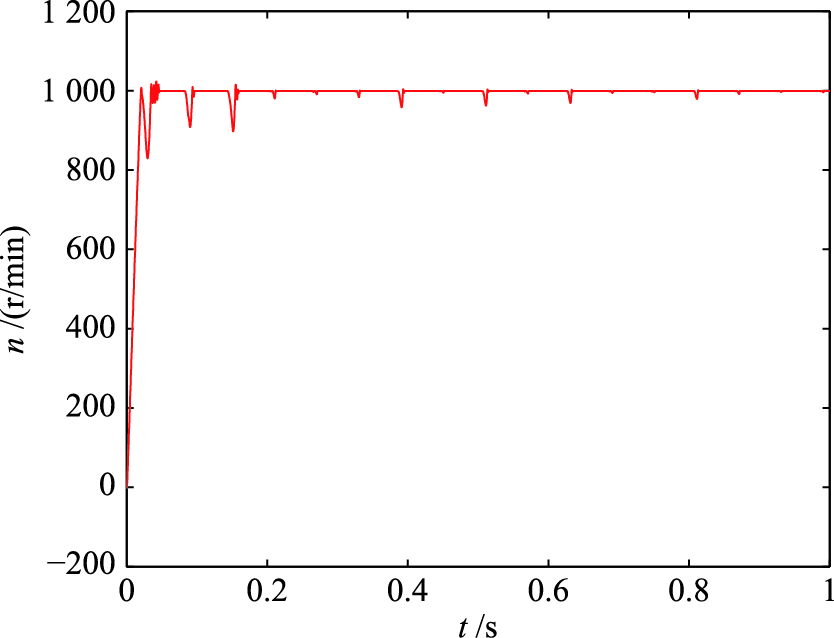 |
| 图 5 系统1转速响应Fig. 5 Speed response of system 1 |
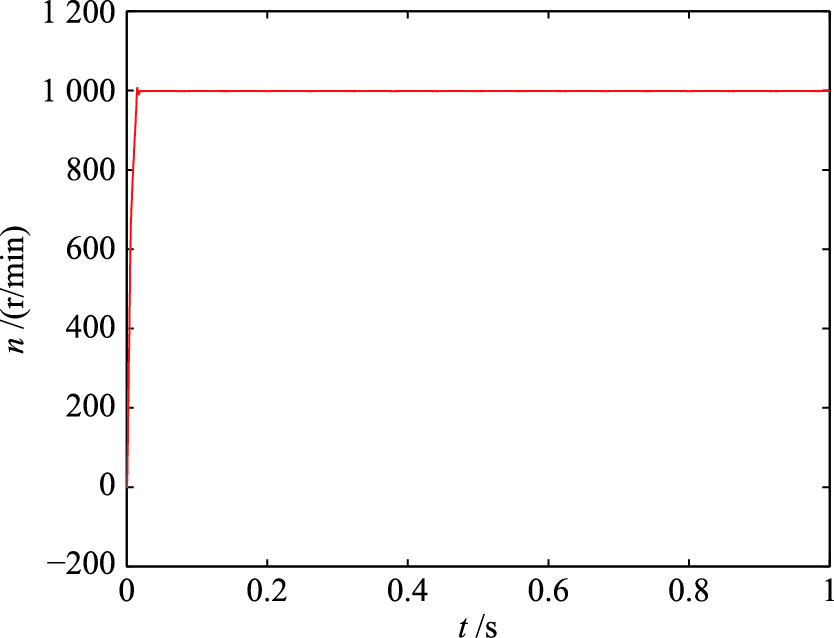 |
| 图 6 系统2转速响应Fig. 6 Speed response of system 2 |
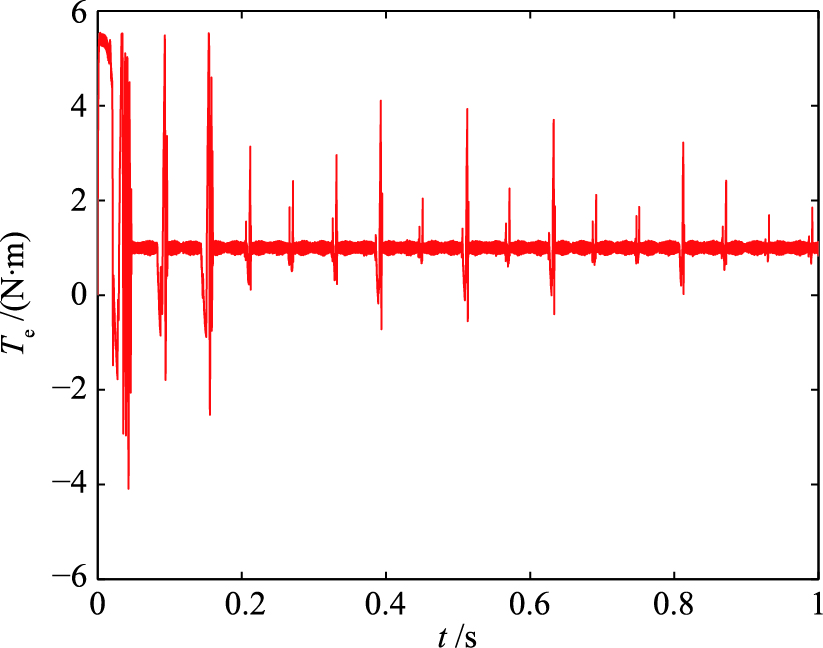 |
| 图 7 系统1转矩响应Fig. 7 Torque response of system 1 |
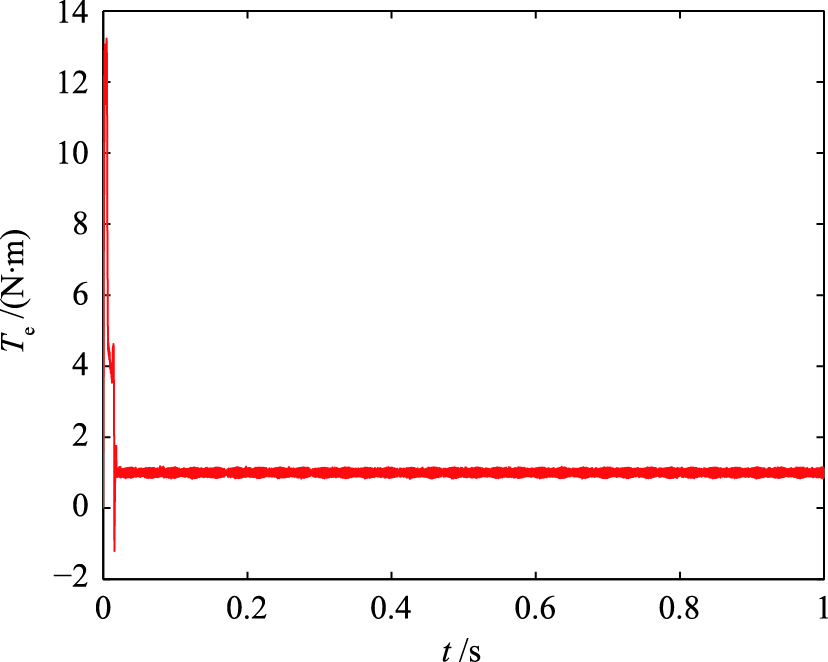 |
| 图 8 系统2转矩响应Fig. 8 Torque response of system 2 |
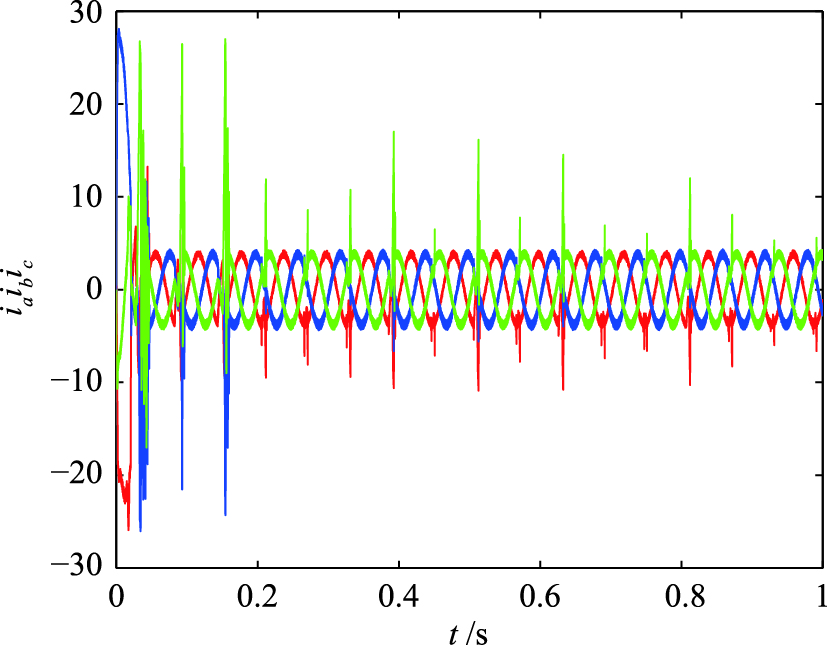 |
| 图 9 系统1三相定子电流响应Fig. 9 Three phase stator current response of system 1 |
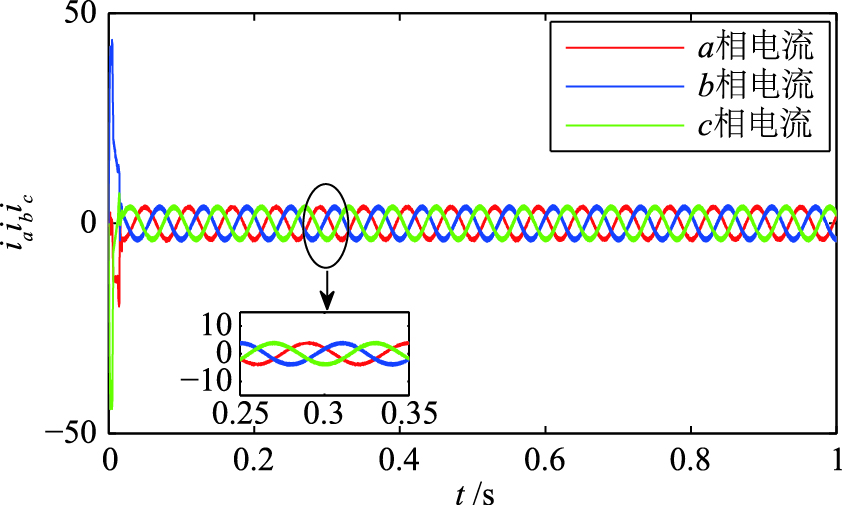 |
| 图 10 系统2三相定子电流响应Fig. 10 Three phase stator current response of system 2 |
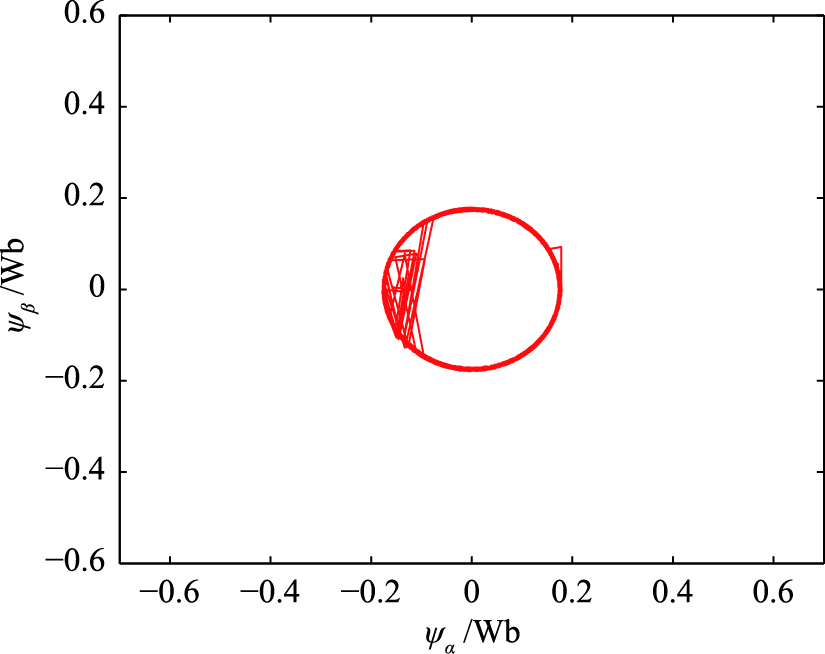 |
| 图 11 系统1定子磁链响应Fig. 11 Stator flux response of system 1 |
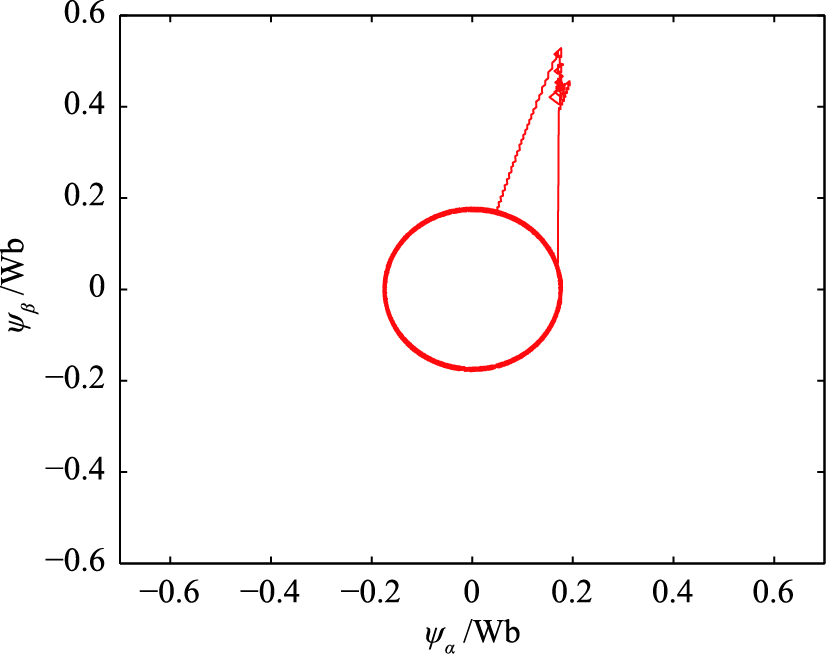 |
| 图 12 系统2定子磁链响应Fig. 12 Stator flux response of system 2 |
仿真结果表明,当电容电压不平衡时,未经过电压补偿的驱动系统的转速、 转矩和三相电流将会产生一些谐波,而电压抑制策略可以对这些谐波进行有效地滤除. 因此,抑制后的系统转速、 转矩和三相电流响应曲线具有良好的运行性能. 整个模型预测转矩控制系统能够使PMSM连续平稳运行. 系统1和系统2的三相定子电流谐波失真(total harmonic distortion,THD)如表 2所示,THD公式定义为
| 相电流 | a相电流 | b相电流 | c相电流 |
| 系统1 | 27.76% | 10.88% | 30.37% |
| 系统2 | 3.13% | 4.55% | 4.61% |
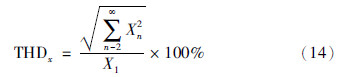
由表 2可知,与不平衡电压未抑制的控制系统相比,采用抑制策略的控制系统三相电流具有更小的THD值. 但是由于模型预测转矩控制权重因子的取值尚未形成完整
的理论,且本文在目标函数中增加的不平衡电压成分无疑对磁链和转速的权重分配产生了影响,因此导致启动时刻的磁链、 三相定子电流与转矩的幅值较大.
5 结论引用三相四开关逆变器作为容错拓扑具有重要的应用价值,本文首先在考虑母线电容分压不平衡的因素下,对容错后的逆变器进行了建模分析; 然后应用模型预测转矩控制策略对三相四开关容错逆变器进行不平衡电压抑制;
最后仿真结果证明基于四开关容错逆变器的模型预测转矩控制策略可以使故障后的驱动系统稳定运行. 而如何解决目标函数的取值,以及降低驱动系统参数对预测精度的影响仍有待进一步研究.
| [1] | Behrooz M. Survey of fault-tolerance techniques for three-phase voltage source inverters[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10): 5192-5202. |
| [2] | 安群涛, 孙醒涛, 赵克, 等. 容错三相四开关逆变器控制策略[J]. 中国电机工程学报, 2010, 30(3): 14-20. An Q T, Sun X T, Zhao K, et al. Control strategy for fault-tolerant three-phase four-switch inverters[J]. Proceedings of the CSEE, 2010, 30(3): 14-20. |
| [3] | Campos-Delgado D U, Espinoza-Trejo D R, Palacios E. Fault-tolerant control in variable speed drives: A survey[J]. IET Electric Power Applications, 2008, 2(2): 121-134. |
| [4] | Mendes A M S, Cardoso A J M. Fault-tolerant operating strategies applied to three-phase induction-motor drives[J]. IEEE Transactions on Industrial Electronics, 2006, 53(6): 1807-1817. |
| [5] | 张兰红, 胡育文, 黄文新. 容错型四开关三相变换器异步发电系统的直接转矩控制研究[J]. 中国电机工程学报, 2005, 25(18): 140-145. Zhang L H, Hu Y W, Huang W X. Research on direct torque control of tolerant type four-switch three-phase converter induction generation system[J]. Proceeding of the CSEE, 2005, 25(18): 140-145. |
| [6] | 孙丹, 贺益康, 何宗元. 基于容错逆变器的永磁同步电机直接转矩控制[J]. 浙江大学学报, 2007, 41(7): 1101-1106. Sun D, He Y K, He Z Y. Fault tolerant inverter based direct torque control for permanent magnet synchronous motor[J]. Journal of Zhejiang University, 2007, 41(7): 1101-1106. |
| [7] | Welchko B A, Lipo T A, Jahns T M, et al. Fault tolerant three-phase AC motor drive topologies: A comparison of features, cost, and limitations[J]. IEEE Transactions on Power Electronics, 2004, 19(4): 1108-1116. |
| [8] | 林海, 严卫生, 李宏. 无刷直流电机驱动控制容错方案研究[J]. 西安交通大学学报, 2009, 43(2): 53-57. Lin H, Yan W S, Li H. Inverter fault-tolerant operation of brushless DC motor drives[J]. Journal of Xi'an Jiaotong University, 2009, 43(2): 53-57. |
| [9] | Hoang K D, Zhu Z Q, Foster M P. Influence and compensation of inverter voltage drop in direct torque-controlled four-switch three-phase PM brushless AC drives[J]. IEEE Transactions on Power Electronics, 2011, 26(8): 2343-2357. |
| [10] | Blaabjerg F, Neacsu D O, Pedersen J K. Adaptive SVM to compensate DC-link voltage ripple for four-switch three-phase voltage-source inverters[J]. IEEE Transactions on Power Electronics, 1999, 14(4): 743-752. |
| [11] | Masmoudi M, El Badsi B, Masmoudi A. DTC of B4-inverter-fed BLDC motor drives with reduced torque ripple during sector-to-sector commutations[J]. IEEE Transactions on Power Electronics, 2014, 29(9): 4855-4865. |
| [12] | Xia C L, Xiao Y W, Chen W, et al. Three effective vectors-based current control scheme for four-switch three-phase trapezoidal brushless DC motor[J]. IET Electric Power Applications, 2013, 7(7): 566-574. |
| [13] | 安群涛. 三相电机驱动系统中逆变器故障诊断与容错控制策略研究[D]. 哈尔滨: 哈尔滨工业大学, 2011. An Q T. Diagnosis and fault-tolerant control strategies of inverters in three-phase motor drive systems[D]. Harbin: Harbin Institute of Technology, 2011. |
| [14] | 蒋志坚, 徐殿国, 朱香娟. 感应电动机四开关低成本逆变器的磁链轨迹改进控制研究[J]. 中国电机工程学报, 2004, 23(11): 74-79. Jiang Z J, Xu D G, Zhu X J. An improved development of four-switch low cost inverter on induction motor with magnetic-flux control method[J]. Proceedings of CSEE, 2003, 23(11): 74-79. |
| [15] | Zhang Y C, Xie W, Li Z X, et al. Model predictive direct power control of a PWM rectifier with duty cycle optimization[J]. IEEE Transactions on Power Electronics, 2013, 28(11): 5343-5351. |
| [16] | Teng Q F, Bai J Y, Zhu J G, et al. Fault tolerant model predictive control of three-phase permanent magnet synchronous motors[J]. WSEAS Transactions on Systems, 2013, 8(12): 385-397. |
| [17] | Preindl M, Bolognani S. Model predictive direct torque control with finite control set for PMSM drive systems, Part 1: Maximum torque per ampere operation[J]. IEEE Transactions on Industrial Informatics, 2013, 9(4): 1912-1921. |
| [18] | Preindl M, Bolognani S. Model predictive direct torque control with finite control set for PMSM drive systems, Part 2: Field weakening operation[J]. IEEE Transactions on Industrial Informatics, 2013, 9(2): 648-657. |
| [19] | Preindl M, Bolognani S. Model predictive direct speed control with finite control set of PMSM drive systems[J]. IEEE Transactions on Power Electronics, 2013, 28(2): 1007-1015. |
| [20] | Sguarezi A J, Ruppert E. Model-based predictive control applied to the doubly-fed induction generator direct power control[J]. IEEE Transactions on Sustainable Energy, 2012, 3(3): 398-406. |
| [21] | Kim J, Hong J, Nam K. A current distortion compensation scheme for four-switch inverters[J]. IEEE Transactions on Power Electronics, 2009, 24(4): 1032-1040. |
| [22] | Wang F X, Zhang Z B, Davari A, et al. An experimental assessment of finite-state predictive torque control for electrical drives by considering different online-optimization methods[J]. Control Engineering Practice, 2014, 31(SI): 1-8. |
| [23] | Sanchez P M, Machado O, Pena E J B, et al. FPGA-based implementation of a predictive current controller for power converters[J]. IEEE Transactions on Industrial Informatics, 2013, 9(3): 1312-1321. |



