1 引言
脑控系统是一种与人的意念和思维相关的新型控制系统,它以人脑为中心,以脑电信号为基础,通过脑—机接口(brain-computer interface,BCI)来实现控制[1]. 脑控系统在残疾人的生活辅助、 肢体损伤者的康复训练、 游戏娱乐、 智能家居和军事等领域都具有很大的研究和应用价值[2, 3, 4, 5, 6]. 基于脑电信号的脑—机接口系统的关键技术就是实现对脑电信号的特征提取和分类.
BCI应用中最常用的脑电信号特征提取方法包括: 时域特征提取(如带通滤波[7]),频域特征提取(如AAR[8]、 小波变换[9]),空域特征提取(如ICA[10]、 CSP[11]). 但是脑控系统中EEG信号却包含多维数据信息,这些算法难以从多维脑电数据中挖掘出更有效的脑电特征. 脑电特征分类算法主要包括贝叶斯分类器[12]、 神经网络[13]、 支持向量机(SVM)[14, 15]等. 目前SVM是在各种BCI系统中应用最广泛的算法,并取得了良好的分类效果.
通常脑电信号识别所采用的方法是: 先对脑电数据进行预处理,然后对经处理后的脑电数据进行特征提取,最后对提取的特征向量进行模式分类. 这种方法的缺陷是: 脑电信号的识别过程复杂,为了方便提取特征,在数据处理过程中剔除的数据有可能隐含着有用的特征信息.
针对这一问题,本文提出利用深度信念网络(DBN)模型[16]进行脑电信号的识别. 深度信念网络(DBN)模型结合了无监督学习和有监督学习的优点,是一种对高维特征向量具有强大分类能力的神经网络,能从粗糙数据中学习到有利于分类的特征. 本文采用DBN模型对脑电信号的粗糙数据进行特征学习并实现正确识别,并与支持向量机(SVM)等方法比较. 实验结果表明深度信念网络(DBN)模型能够学习到有效的特征并提高识别率,相比传统方法,提供了一种新颖高效的算法.
2 基于Emotiv的脑电信号采集系统脑电信号采集是研究脑电信号的处理与应用的必备环节,一般是通过带有电极的脑电帽获取. 目前研究运动想象脑电信号,如果电极按国际10-20标准分布,一般选取5个相关通道来采集脑电信号,如图 1(a)所示的Fz、 C3、 Cz、 C4、 Pz等通道. 本文所使用的脑电信号采集仪器是由美国Emotiv System公司开发的Emotiv脑电采集仪. 电极是按照国际10-20标准电极安放法安放,其安放位置如图 1(b)所示. Emotiv脑电采集仪的14个电极的安放位置分别是AF3、 F7、 F3、 FC5、 T7、 P7、 O1、 O2、 P8、 T8、 FC6、 F4、 F8、 AF4,参考电极“CMS”和“DRL”是在P3和P4位置,经过多次试验,发现选取4个相关通道的脑电信号效果明显,即选取FC5、 T7、 T8、 FC6等4个通道. 该脑电采集仪的采样频率为128 Hz.
 |
| 图 1 脑电信号通道分布Fig. 1 Channel distribution of EEG |
本文设计了采集这些脑电信号的实验,并在一个较安静的环境下,选取了6名受试者分别进行实验. 其中某个受试者的单次实验过程如图 2所示,具体过程如下: 在实验开始(t=0)时,受试者静坐在椅子上,并保持放松状态; t=2 s时,受试者将听到一个左手或者右手的声音,然后受试者将进行相应的想象左手或者右手运动的实验任务; 当t=4 s时,受试者将听到一个停止的声音,然后受试者才能停止实验任务,并在短暂的休息之后,准备下次实验.
 |
| 图 2 单次实验过程Fig. 2 An experimental process |
在整个实验过程中,对每个受试者的左手运动想象和右手运动想象两类任务采集实验数据. 对于这些采集到的脑电信号,本文只选取了实验第3 s到第4 s时间段的脑电信号作为实验样本,即每组实验样本只有128个数据. 对于每类脑电信号的实验样本按一定比例分为两部分,一部分作为训练数据,一部分作为测试数据. 图 3给出了其中一名受试者想象左右手运动时,FC5通道的脑电信号波形图.
 |
| 图 3 FC5通道脑电信号的波形Fig. 3 EEG waveform of FC5 channel |
受限玻尔兹曼机(RBM)是构建深度信念网络(DBN)的基本结构,它是一个具有两层结构的无向图模型,如图 4所示.
 |
| 图 4 受限玻尔兹曼机Fig. 4 Restricted Boltzmann machine |
在RBM中,可视层为二进制随机单元v∈{0,1}D,隐藏层为二进制随机单元h∈{0,1}F,可视层和隐藏层是全连接的,状态{v,h}的能量表示义为

其中θ={W,b,a}是模型参数: Wij是可视单元i与隐藏单元j之间的连接权重; bi和aj是偏置项.
在第一层即第一个可视层(即为输入层),将采集的脑信号作为输入. 在堆叠的RBM结构中,第一层和第二层为一个RBM,其中第一层为可视层,第二层为隐藏层. 在第二层和第三层组成的第二个RBM中,第二层为可视层,而第三层为隐藏层,以此类推. 因此每一个隐藏层的神经元节点是伯努利随见变量,由可视层激活:

可视单元和隐藏单元的联合分布被定义为


Z(θ)被称为归一化常数,可视向量v的模型分布概率为

由于RBM特殊的结构,隐藏单元可以被显式地边缘化为
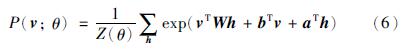
从式(3)中很容易得出隐藏单元h和可视单元v的条件概率分布:



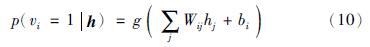
其中g(x)=1/(1+exp(-x))是S型激活函数.
3.2 对比散度(CD)快速学习算法在实际中,权值的更新是通过目标函数的梯度的近似来完成的,这种算法被称为对比散度(CD)[18],Hinton指出,当使用训练数据来初始化观测数据v0时,只需要通过k(通常k=1)步Gibbs采样就能得到足够好的近似. 在进行初始化时,将可视单元的状态设置为一个训练样本,通过式(9)计算所有隐藏单元的激活状态,再根据式(10)计算出第i个可视单元vi取值为1的概率,由此便产生了一个可视层的重构. 这时,参数的更新准则变为



其中α为学习率,Precon表示一步重构后模型定义的一个分布. 脑电信号的多层RBM的重构过程可描述为图 5.
 |
| 图 5 脑电信号重构过程Fig. 5 Reconstruction process of EEG |
CD快速算法的流程:
Step 1 初始化可视单元的状态为v1=x0,W、 a、 b为随机的较小数值;
Step 2 计算隐藏单元的状态分布p(h1j=1丨v1)=g Wijv1i+aj,从条件分布P(h1丨v1)中抽取h1j∈{0,1};
Wijv1i+aj,从条件分布P(h1丨v1)中抽取h1j∈{0,1};
Step 3 计算可视单元的状态分布p(v2i=1丨h1)=g Wijh1i+bi,从条件分布P(v2丨h1)中抽取v2i∈{0,1};
Wijh1i+bi,从条件分布P(v2丨h1)中抽取v2i∈{0,1};
Step 4 计算隐藏单元的状态分布p(h2j=1丨v2)=g Wijv2i+aj;
Wijv2i+aj;
Step 5 按照式(11)~式(13)参数更新准则更新各个参数.
3.3 深度信念网络结构深度信念网络(DBN)由多个限制玻尔兹曼机(restricted Boltzmann machines)组成,是一个包含多个隐藏层的概率生成模型,一个典型的深度信念网络如图 6所示.
 |
| 图 6 DBN网络结构图Fig. 6 The structure of deep belief network |
深度信念网络的训练可以分成两个阶段[17],最开始的时候,通过一个非监督贪婪逐层训练方法去预训练每一层以获得生成模型的权值,再用有监督的BP算法对整个网络进行微调.
深度信念网络的每层含多个神经元,计算时将每层的输出作为下层网络的输入,通过CD来学习每层RBM的参数. 最底层的输入是脑电信号数据. 可视层与第一层隐藏层形成一个RBM,通过贪婪逐层训练算法,使得RBM达到能量平衡. 然后将这个RBM的输出,即第1层隐藏层作为下一个RBM的输入,并单独进行参数调整,使得第2个RBM也达到能量平衡,后面的每一层都用同样的方法进行训练,直到最后一个RBM训练完成.
BP网络将RBM提取的特征向量进行分类,并微调DBN网络. 其训练过程是: 先通过前向传播,将输入特征向量沿输入端传播到输出端; 然后是反向传播,将BP的输出结果与正确结果相比得到的误差从输出端反向传播至输入端,以修改DBN的参数.
4 实验与分析 4.1 参数设置参数的设置对RBM的训练效果具有很大的影响,对于特定的RBM结构和数据集,不合理的参数设置会导致建模困难.
(1) 小批量数据及其容量. 由于式(11)~式(13)更新时计算量很大,为了提高计算效率,将训练集分成小批量的数据进行处理.
(2) 学习率. 如果学习率设置得太大,则重构误差会随之增大,权重也会变化很快,一般设权重的更新值为权重的10-3倍左右. 当有一个单元的输入值很大的时候,为了避免同一方向上较多小的波动引起梯度符号的改变,权重的更新速度应该更慢一些. 此处学习率设置为0.1.
(3) 动量学习率. 选择合适的学习率α非常重要,如果学习率太大,权重更新得太快可能导致算法不稳定,但如果学习率太小,收敛速度就会很慢. 为了解决这一问题,可以在参数更新公式中添加动量项(momentum)k,再加上本次似然函数的梯度方向来更新本次的参数增量. 这样能够避免过早地收敛到局部最优点. 这时参数W的更新公式为

参数a和b的更新方法与W一样,这里的k就称为动量学习率,此处设置为0.6.
(4) 权重衰减. 为了避免出现过拟合现象,通常需要在梯度项后面增加一项惩罚函数来惩罚较大的参数值,这就是权值衰减策略. (λ/2)
 Wij2是最简单的惩罚函数,需要注意的是,为了避免学习率发生变化时优化的目标函数也发生变化,惩罚项前面也应该乘上学习率,这时权值更新的公式为
Wij2是最简单的惩罚函数,需要注意的是,为了避免学习率发生变化时优化的目标函数也发生变化,惩罚项前面也应该乘上学习率,这时权值更新的公式为
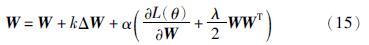
实验采集了120组数据,选取60组数据作为训练样本,剩下的60组样本作为测试样本. 为了便于对比分析,实验中用到了两种数据,一是直接采集的粗糙数据,二是用共同空间模式(CSP)算法提取的特征数据. 深层网络、 极限学习机和支持向量机的参数通过5-fold交叉验证的方法确定. 为了将深度学习的方法与传统的先经过特征提取,再进行分类的方法进行对比. 采用了4种识别方法.
方法1 粗糙数据+DBN. 由于神经网络节点数的增多可以提高网络的逼近能力,但会使得网络的泛化能力降低,所以节点数应该逐层降低维度,提高神经网络的泛化能力,且降维的幅度不宜过大,否则容易丢失重要信息,导致结果剧烈震荡[19]. 因此用试探法,通过多次试验找出一个最优的深度信念网络结构,即有3个隐含层,隐层节点为500-200-30(DBN).
方法2 粗糙数据+自动编码机(AE). AE设置为与DBN相同的层数三层. 其第一层的节点数必须和数据的输入维度保持一致,此处为128. 最后一层也必须和输出维度保持一致,此处为1. 即其结构为128-14-1(AE).
方法3 特征数据+极限学习机(ELM). 极限学习机[20]是一种高效的前馈神经网络,具有良好的分类能力. 此处用极限学习机对脑电数据进行特征分类. 其隐藏层最佳节点为20,核函数采用Sigmoid函数.
方法4 特征数据+SVM. SVM被广泛应用于脑电数据特征分类,且效果较好. 此处SVM的核函数采用RBF核函数. SVM最优的参数为C=2 048和γ=2.
对于不同的受试者在不同方法下的正确识别率如表 1所示.
| 方法 | DBN | AE | CSP+ELM | CSP+SVM |
| 受试者1 | 94.91% | 90.36% | 89.17% | 88.33% |
| 受试者2 | 90.89% | 89.76% | 82.50% | 83.33% |
| 受试者3 | 89.24% | 85.42% | 83.33% | 81.67% |
| 受试者4 | 90.55% | 88.33% | 83.33% | 85.00% |
| 受试者5 | 95.00% | 89.17% | 88.33% | 88.88% |
| 受试者6 | 90.89% | 88.88% | 85.00% | 83.33% |
| 训练时间 | 2.279 3 s | 1.839 2 s | 0.031 2 s | 1.583 7 s |
| 测试时间 | 0.019 2 s | 0.011 5 s | 0.000 1 s | 0.009 8 s |
从表 1可以看出,在对左右手运动想象脑电信号的识别中,不同的受试者脑电正确识别率有一些差异. 这是因为脑电采集对象不同,和采集过程中噪声大小的不同造成的. 但是仍能看出,采用深度学习方法,可以得到很好的脑电信号的识别率,其中采用深度信念网络学习脑电信号特征的方法可以获得最好的识别效果. DBN相对传统的方法,识别的正确率有很大的提高,以受试者1为例,分别超过CSP+ELM的识别率5.74%,超过CSP+SVM的识别率6.58%.
表 1中,训练时间和测试时间值是通过计算6个受试者得训练时间和测试时间的平均值. 尽管脑机接口控制系统对在线实时处理单个样本信号的处理时间要求很严格,但是通常采取离线训练模型在线使用的方式,因此对模型的训练时间不敏感,更侧重的是测试的时候对信号的处理时间. 虽然DBN算法的测试时间相比其他算法是最大的,但是也只有0.019 2 s,也能达到一个很快的速度,可以满足控制系统的要求.
但是对于DBN而言,由于这一新兴领域目前还没有完整的调节各个参数的理论,很大程度上取决于自身的经验,通过调节获得较优的参数,才能构造出一个优秀的网络结构.
5 结论与展望将深度信念网络(DBN)用于脑电信号的识别是一种全新的思路,DBN对高维特征向量具有很强的特征学习能力,其深层结构有助于提取出更抽象、 更具可分类性的特征. 本文设计的实验证明了DBN能够从运动想象脑电信号的粗糙数据中学习到有用特征并实现正确分类,通过对不同受试者的测试表明,基于DBN方法的脑电识别,其分类效果优于先通过CSP进行特征提取,再用ELM、 SVM等进行分类的方法. 对采集到的粗糙脑电数据不需要数据预处理和特征提取等复杂流程,直接运用DBN就能得到很好的识别效果. 然而,本文还只是对左右运动想象脑电信号的识别,将来的工作可以在以下几个方面继续进行: 通过实验采集更多种类的实验样本数据,将深度信念网络用于识别复杂的脑电信号; 通过进一步研究优化网络的结构和参数的理论,不断优化网络结构和参数,从而提高脑电信号的识别能力.
| [1] | 王行愚, 金晶, 张宇, 等. 脑控: 基于脑—机接口的人机融合控制[J]. 自动化学报, 2013, 39(3): 208-211. Wang X Y, Jin J, Zhang Y, et al. Brain control: Human-computer integration control based on brain-computer interface[J]. Acta Automatica Sinica, 2013, 39(3): 208-211. |
| [2] | Kao J C, Stavisky S D, Sussillo D, et al. Information systems opportunities in brain-machine interface decoders[J]. Proceedings of IEEE, 2014, 102(5): 666-682. |
| [3] | Yao L, Meng J J, Zhang D G, et al. Combining motor imagery with selective sensation toward a hybird-modality BCI[J]. IEEE Transactions on Biomedical Engineering, 2014, 61(8): 2304-2312. |
| [4] | Chae Y W, Jeong J S, Jo S H. Toward brain-actuated humanoid robots: Asynchronous direct control using an EEG-based BCI[J]. IEEE Transactions on Robotics, 2012, 28(5): 1131-1144. |
| [5] | Tomita Y, Vialatte F B. Bimodal BCI using simultaneously NIRS and EEG[J]. IEEE Transactions on Biomedical Engineering, 2014, 61(4): 1274-1284. |
| [6] | Kim M, Kim B H, Jo S. Quantitative evaluation of a low-cost noninvasive hybrid interface based on EEG and eye movement[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2015, 23(2): 159-168. |
| [7] | Citi L, Poli R, Cinel C, et al. P300-based BCI mouse with genetically-optimized analogue control[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2008, 16(1): 51-61. |
| [8] | Schlogl A, Lee F, Bischof H, et al. Characteriza-tion of four-class motor imagery EEG data for the BCI-competition 2005[J]. Journal of Neural Engineering, 2005, 2(4): 14-22. |
| [9] | Wu Z H, Yao D H. Frequency detection with stability co-efficient for steady-state visual evoked potential (SSVEP)-based BCIs[J]. Journal of Neural Engineering, 2008, 5(1): 36-43. |
| [10] | Chuang C H, Ko L W, Lin Y P, et al. Independent component ensemble of EEG for brain-computer interface[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2014, 22(2): 230-238. |
| [11] | Wang X H. Optimizing spatial filters for single-trial EEG classification via a discriminate extension to CSP: the Fisher criterion[J]. Medical and Biological Engineering and Computing, 2011, 49(9): 997-1001. |
| [12] | Lemm S, Schafer C, Curio G. BCI competition 2003-Data set III: Probabilistic modeling of sensorimotor mu rhythms for classification of imaginary hand movements[J]. IEEE Transactions on Biomedical Engineering, 2004, 51(6): 1077-1080. |
| [13] | Balakrishnan D, Puthusserypady S. Multilayer perceptrons for the classification of brain computer interface data[C] //Proceedings of the IEEE 31st Annual Northeast on Bio-engineering Conference. Piscataway, NJ, USA: IEEE, 2005: 118-119. |
| [14] | Gu Z H, Yu Z L, Shen Z F, et al. An online semi-supervised brain-computer interface[J]. IEEE Transactions on Biomedical Engineering, 2013, 60(9): 2614-2623. |
| [15] | Berta R, Bellotti F, De Gloria A, et al. Electroencephalogram and physiological signal analysis for assessing flow in games[J]. IEEE Transactions on Computational Intelligence and AI in Games, 2013, 5(2): 164-175. |
| [16] | Hinton G, Salakhutdinov R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(504): 504-507. |
| [17] | Hinton G, Osindero S, Teh Y. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527-1554. |
| [18] | Hinton G E. Training products of experts by minimizing contrastive divergence[J]. Neural Computation, 2002, 14(8): 1711-1800. |
| [19] | Xia K W, Li C B, Shen J Y. An optimization algorithm on the number of hidden layer nodes in feed-forward neural network[J]. Computer Science, 2005, 32(11): 143-145. |
| [20] | Huang G B, Zhou H M, Ding X J, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2012, 42(2): 513-529. |



