2. 中国石油天然气管道第二工程公司第六管道安装分公司, 江苏 徐州 221000;
3. 大庆油田有限责任公司天然气分公司, 黑龙江 大庆 163318
2. The Sixth Pipe Installation Branch Company, the Second Engineering Company of China Petroleum Natural Gas Pipeline, Xuzhou 221000, China;
3. Natural Gas Branch Company of Daqing Oilfield Co. Ltd, Daqing 163318, China
1 引言
确定机采井的检泵策略,最重要的是合理地预防检泵周期. 确定机采井检修周期的主要依据是其磨损故障规律. 当机采井的检泵周期不符合实际需求时,会出现因没有得到及时检修而造成失修,增加事后检修的工作量; 或者出现因得到不必要的检修而造成过修,从而提高检修的总体成本. 因此,一个合理的预防性检泵周期对于机采井检泵策略至关重要,确定机采井最佳预防性检泵周期的核心是确定其故障率函数[1, 2, 3].
复杂设备故障率曲线是设备故障率预测和故障诊断的重要参数依据,因此研究复杂设备故障率曲线的变化规律具有重要意义和应用价值[4]. Rodrigo[5]指出设备故障率曲线的形状能揭示设备的故障机理或者对应于设备特定的使用阶段,因此对故障率的预测和控制有积极效果; Xie[6]运用扩展威布尔模型建立故障率曲线并给出参数估计方法,为故障率曲线建模提供了新的思路和方法; Savsar[7]对基于恒定故障率的柔性制造单元的运行数据进行数学建模研究. 机采井是集机、 电、 液于一体的复杂设备,采用基础分布模型建模不能全面呈现出机采井故障率曲线规律. 由于威布尔分布被广泛应用于各类故障分布数据处理中,且其主要适用于机电类复杂设备的磨损累计故障的分布建模,因此本文采用3参数的威布尔分布模型对机采井检泵周期数据进行建模分析.
在对机采井检泵周期数据进行分析时,首先假设其检泵周期服从威布尔分布,并运用基于模糊粒子群模拟退火算法的相关系数法对威布尔分布的3个参数进行估计,通过K-S检验法对假设进行验证,得出其检泵周期服从威布尔分布,并通过可靠度函数得出其故障率函数; 然后考虑安全最高、 经济费用最少和可用度最大等影响因素,运用模糊决策法计算得出其最佳预防性检泵周期; 最后结合最佳预防性检泵周期和目前油田机采井的检泵策略,确定机采井的最佳预防性检泵策略.
2 油田机采井故障率函数确定为确定机采井的故障率函数,首先分析其检泵周期数据,得出机采井故障发生的概率密度图,并根据曲线趋势假设其故障规律服从威布尔分布; 然后建立机采井检泵周期分布模型,运用基于智能算法对威布尔分布参数进行估计; 最后利用数理统计检验法对提出的假设进行检验,进而确定机采井检泵周期服从的分布函数、 概率密度函数及其可靠度函数. 通过计算机采井故障概率密度函数与可靠度函数的比值[8],从而得到机采井的故障率函数. 机采井故障率函数确定流程如图 1所示.
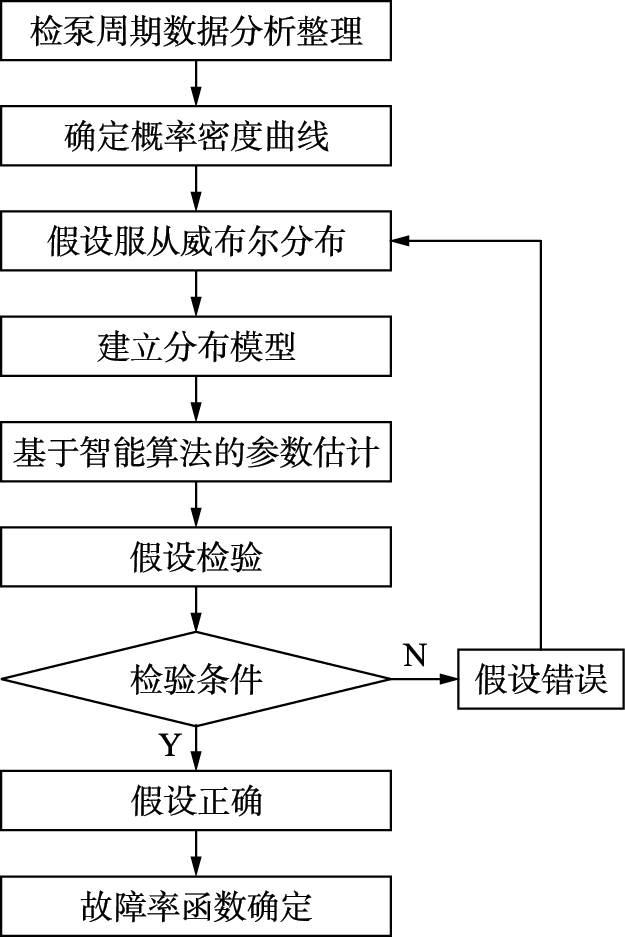 |
| 图 1 机采井故障率函数确定流程图Fig. 1 Determination flow diagram of failure rate function of the pump recovery well |
机采井检泵周期主要是指机采井相邻两次故障检泵停泵日期之间的无故障采油的天数,也就是机采井的无故障工作时间. 本文采集同一区块15台机采井,这些机采井均为2000年11月下泵的新井,数据来自从2000年11月到2013年11月这13年间采集的检泵周期.
机采井检泵周期数据共有150组现场数据,设n=150. 将样本数据均分成m组,并从小到大排序,分组数[9]k=1+ln n/ln2=1+3.32lnn=8.228 8,因此取k=9. 把样本数据分为9组,选取T0=30,Tk=1 290,则每组时间区间的间隔Δt=(Tk-T0)/k=140 d. 数据如表 1所示. 由表 1中第1组数据可知,在第一时间区间中有3个数据,经与现场人员核实,这3个数据是抽查部分井各部件而进行的调查检泵,由于这3个数据不属于故障检泵周期,因此将不考虑这3组数据. 根据统计各组的频数和频率,分别以表 1中的区间中值为横坐标,每组频率和累计频率为纵坐标,拟合出检泵周期的分布函数F(t)的曲线离散点图,如图 2所示; 概率密度函数f(t)的曲线离散点图,如图 3所示.
| 序号 | 时间区间/d | 区间中值 | 频数 | 频率 | 累计频率 |
| 1 | 30, 170 | 100 | 3 | 0.020 0 | 0.020 0 |
| 2 | 170, 310 | 240 | 46 | 0.306 7 | 0.326 7 |
| 3 | 310, 450 | 380 | 32 | 0.213 3 | 0.540 0 |
| 4 | 450, 590 | 520 | 21 | 0.140 0 | 0.680 0 |
| 5 | 590, 730 | 660 | 17 | 0.113 3 | 0.793 3 |
| 6 | 730, 870 | 800 | 13 | 0.086 7 | 0.880 0 |
| 7 | 870, 1 010 | 940 | 9 | 0.060 0 | 0.940 0 |
| 8 | 1 010, 1 150 | 1 080 | 6 | 0.040 0 | 0.980 0 |
| 9 | 1 150, 1 290 | 1 220 | 3 | 0.020 0 | 1.000 0 |
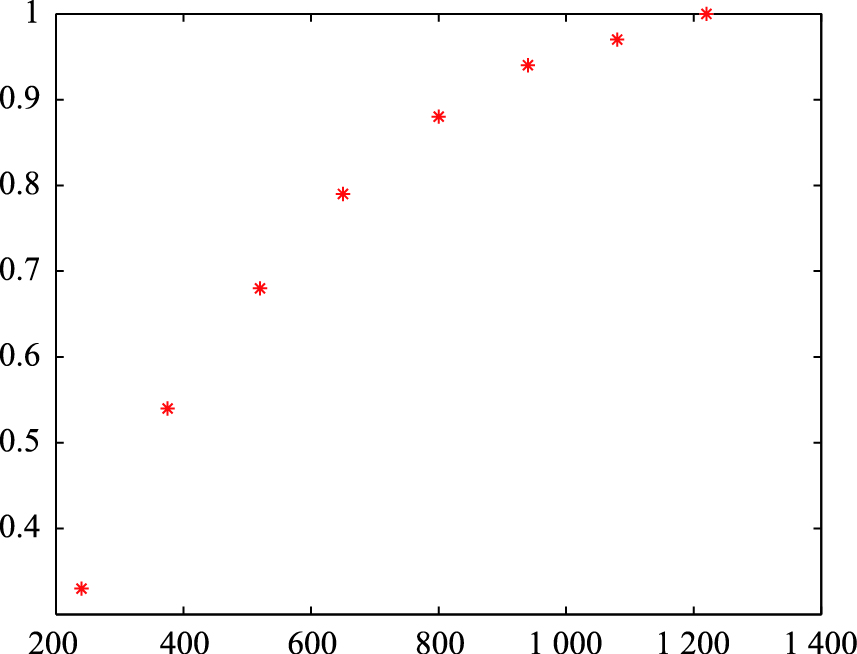 |
| 图 2 F(t)散点图Fig. 2 Scatter diagram of F(t) |
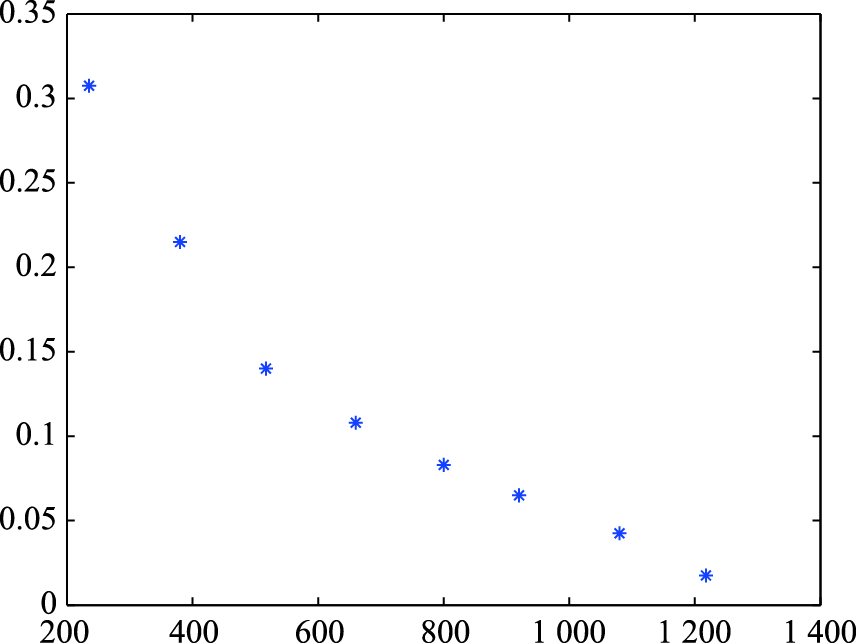 |
| 图 3 f(t)散点图Fig. 3 Scatter diagram of f(t) |
由图 3可知,机采井的检泵周期概率密度函数是单调下降. 在数理统计中,该曲线呈单调下降趋势的只有威布尔分布和指数分布,由于当3参数威布尔分布中位置参数为0、 形状参数为1时,威布尔分布可以简化为指数分布[10],因此可假设该样本数据服从威布尔分布.
2.2 机采井故障率分布模型参数估计假设机采井的检泵周期服从3参数威布尔分布,而威布尔分布的参数估计比较复杂[11, 12, 13, 14],因此采用基于模糊粒子群—模拟退火(fuzzy particle swarm optimization-simulated annealing,FPSO-SA)算法的威布尔分布参数估计[15].
2.2.1 FPSO-SA算法在粒子群寻优过程中,惯性权值因子直接影响粒子群的全局和局部搜索能力,标准粒子群算法处理粒子群的“聚集”现象效果不明显,因此将模糊理论引入粒子群算法中得到FPSO算法. 从粒子个体纵向和横向运动的特性出发,引入粒子个体的进化度因子和离散度因子,运用这两个参数因子通过模糊规则和模糊推理实现惯性权值因子的动态调整. 将FPSO算法与SA算法相结合得到FPSO-SA算法,从而解决粒子群的“早熟”问题,利用降温策略和迭代步数使FPSO算法收敛到全局最优值.
FPSO-SA算法的状态生成机制是将FSPO算法的更新公式作为SA算法的状态生成函数,根据粒子群向全局最优位置运动的轨迹特性产生FPSO-SA算法的新状态,以便提高新状态的有效性,降低无效状态出现的频率. FPSO-SA算法的状态选择机制是Metropolis算法反复以状态迁移概率接受FPSO-SA算法产生的新状态,直到粒子群到达全局最好位置. 同时Metropolis算法允许FPSO-SA算法产生的状态充分震荡,并能以一定的概率接受粒子个体向非全局最好位置方向移动.
FPSO-SA算法的实现过程如下:
Step 1: 初始化SA算法的冷却进度表,其中包括初始温度T0、 终止温度Tend、 降温策略和每个温度下迭代代数L; 同时初始化FPSO算法的粒子群规模m、 迭代代数n、 各粒子的初始速度Vi、 位置Xi和适应度函数-|ρ(γ)|;
Step 2:令分组数k=1;
Step 3: 运用FPSO算法产生一个新状态,即各粒子搜索到新的位置X′i(k);
Step 4: 将各粒子当前位置的适应值-|ρ(X′i(k))|与其经过的个体最好位置Xipbest(k)的适应值-|ρ(Xipbest(k))|进行比较,令ΔS=-|ρ(X′i(k))|-(-|ρ(Xipbest(k))|);
Step 5: 运用Metropolis算法,若ΔS<0,无条件接受当前位置为最好位置,令Xipbest(k)=X′i(k); 若ΔS≥0,则以概率p=exp(-ΔS/T0)接收当前位置为最好位置Xipbest(k)=X′i(k); 同理,对粒子群的全局最好位置进行更新;
Step 6:判断是否满足算法终止条件,如果满足,输出当前最好位置Xgbest(k)和当前位置所对应的最优线性相关系数-|ρ(Xgbest(k))|; 如果不满足令k=k+1;
Step 7:判断当前迭代代数,若k≤L,转到Step 3; 若k>L,对当前温度进行降温,转到Step 2,直到满足算法终止条件为止.
2.2.2 基于FPSO-SA算法的威布尔分布参数估计若随机变量t服从3参数威布尔分布,记为t~W(α,β,γ),其概率密度函数[16, 17, 18]如式(1)所示,分布函数如式(2)所示.
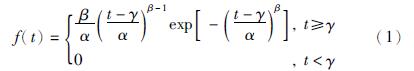
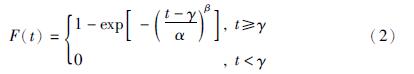
先假定位置参数γ已知,通过最小二乘法将威布尔分布转化为线性方程,并将其线性相关系数ρ表示为γ的函数,γ的值必须满足线性相关系数的绝对值取最大,即
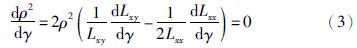
由于上式直接计算复杂,因此采用FPSO-SA算法确定威布尔分布的线性相关系数和最优位置参数的最优值.
将威布尔分布线性相关系数函数ρ(γ)的绝对值取负作为FPSO-SA算法的适应度函数,取值范围满足-1≤-|ρ(γ)|≤0. γ作为算法寻优变量,通过算法的粒子群寻找全局最好位置γ,使适应度函数-|ρ(γ)|取最小值. 当适应度函数取-1时,算法输出当前粒子群的全局最好位置即为最优位置参数估计值,再通过线性方程和待定系数法计算得出威布尔分布另外两个参数的估计值.
通过Matlab软件编写程序实现FPSO-SA算法确定线性相关系数,各参数取值为c1=c2=2.494 45,m=20,ω0=0.6,T0=100,Tend=0.01,L=300,降温策略取T(k)=0.95T(k-1),算法终止条件是连续5次全局最好位置没有变化,适应度函数取-|ρ(γ)|,位置参数取值范围满足0≤γ≤171. 采用FPSO-SA算法得到的参数估计结果为: |ρ|=0.927 6,α=378.731 5,β=1.619,γ=147.230 6.
为了验证线性方程中X和Y之间是否真的线性相关,需要对其进行线性相关性验证. 只要满足|ρ|>ρα,则认为X和Y之间是线性相关的,其中ρα是相关系数临界值,可以通过查找相关系数临界值表获得. 当显著性水平α=0.1时,相关系数临界值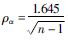 ; 当n=147,显著性水平α=0.1时,相关系数临界值ρα=0.136 1,而|ρ|=0.927 6,满足|ρ|>ρα,因此认为X和Y之间是线性相关的.
; 当n=147,显著性水平α=0.1时,相关系数临界值ρα=0.136 1,而|ρ|=0.927 6,满足|ρ|>ρα,因此认为X和Y之间是线性相关的.
统计法是假设检验的方法之一,是基于大量实验数据统计得出的[19],符合对机采井检泵周期分布假设的检验思路,由于K-S检验法适用于小样本假设检验,检验精度相对较高,因此采用K-S检验法对机采井检泵周期分布函数进行检验.
K-S检验法是将n组样本数据从小到大排序,根据原假设计算每个数据对应的F0(ti),然后与经验分布函数Fn(ti)进行比较,找出这些差值中的绝对值的最大值,再将这个最大值作为检验统计量Dn的样值. 然后将Dn的每一个样值与临界值Dn,α进行比较,满足式(4)则接受假设,否则拒绝假设[20].
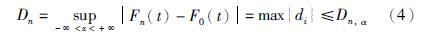
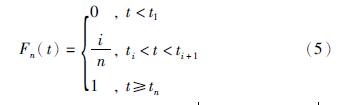
由式(4)和式(5)推出 其中Dn,α表示临界值,当n=147,显著性水平α=0.1时,K-S检验临界值为
其中Dn,α表示临界值,当n=147,显著性水平α=0.1时,K-S检验临界值为 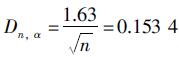
由K-S检验法得到的假设检验数据可知,Dn的每一个样值都小于Dn,α,满足式(4),因此假设成立,机采井检泵周期服从威布尔分布.
2.4 机采井故障率函数确定经上述分析可得,机采井检泵周期服从尺度参数α=378.731 5、 形状参数β=1.619和位置参数γ=147.230 6的参数威布尔分布,其概率密度函数f(t)和分布函数F(t)分别如式(6)和式(7)所示.
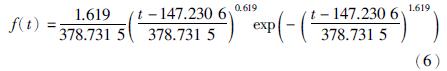
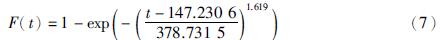
根据机采井检泵周期概率密度函数和分布函数推导出机采井可靠度函数和故障率函数,机采井可靠度函数曲线如图 4所示,机采井故障率函数曲线如图 5所示. 机采井可靠度函数R(t)和故障率函数λ(t)分别如式(8)和式(9)所示.
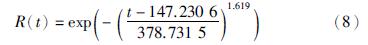
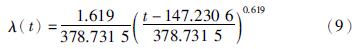
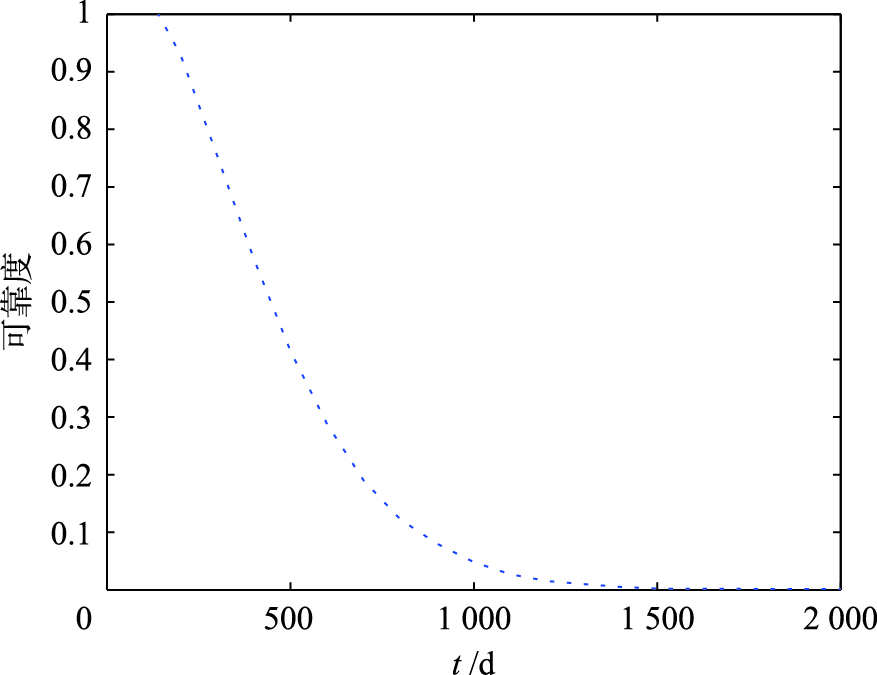 |
| 图 4 机采井可靠度曲线Fig. 4 Reliability curve of the pump recovery well |
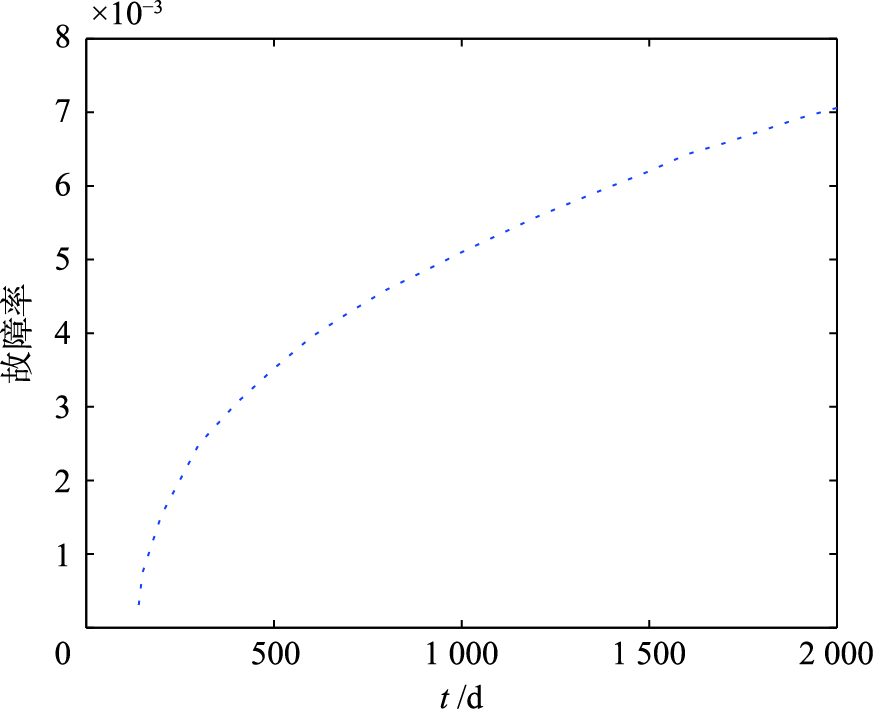 |
| 图 5 机采井故障率曲线Fig. 5 Failure rate curve of the pump recovery well |
由于形状参数值大于1,说明机采井随时间的增加,可靠度会逐渐降低,故障率会逐渐升高,且其故障率随着时间增加变化逐渐缓和,即故障率的变化率逐渐变小. 由图 4可知,机采井起初可靠度较高,可是前期下降很快,但随着时间增加,可靠度下降缓慢且曲线趋于平稳,最终无限趋于最小值0. 由图 5可知,机采井起初故障率较小,但上升速率较快,中后期曲线趋于平稳上升,总体故障率曲线呈现前陡峭后平稳的态势.
3 机采井最佳预防性检泵周期确定 3.1 3类预防性检泵周期分析机采井的预防性检泵,合理的预防性检泵周期是关键. 以下将从安全最高、 经济费用最少和可用度最大这3方面定性分析和确定机采井预防性检泵周期.
3.1.1 安全性最高预防性检泵周期机采井因故障产生危险,此时预防性检泵周期称为安全检泵周期,其公式为

其中,MTTF为机采井平均故障时间(mean time to failure),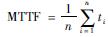 ; Nf为安全分散度,一般取1.5~2,可根据机采井故障严重程度取值.
; Nf为安全分散度,一般取1.5~2,可根据机采井故障严重程度取值.
在检泵周期T内,用cn表示机采井作业检泵维修费用

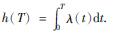 .
.
考虑事后检泵和预防性检泵所消耗的时间,式(11)对T求导,令导数等于0,得式(12),计算机采井在T内检泵成本最低的检泵周期,如式(13)所示.
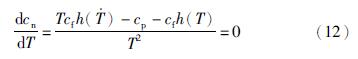

针对机采井出现的故障,常采用更换或维修部件的方法,所以在机采井作业期内,假设其故障率分布不变,则式(13)可以改写为
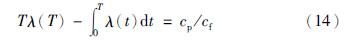
将服从3参数威布尔分布的机采井故障率函数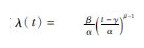 代入式(14)则推导出经济费用最少的预防性检泵周期为
代入式(14)则推导出经济费用最少的预防性检泵周期为
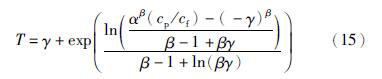
其中,α=378.731 5,β=1.619,γ=147.230 6.
3.1.3 可用度最大预防性检泵周期
在机采井定期检泵的情况下,令Tp为平均预防性检泵时间, Tf为平均事后检泵时间,则在一个周期T内,机采井的平均不能工作时间为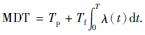 在一个周期内,平均可能工作时间为MUT=T. 根据可用度的概念,可得
在一个周期内,平均可能工作时间为MUT=T. 根据可用度的概念,可得
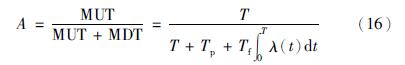
为使可用度最大,将式(16)对T求导,并令其等于0得:
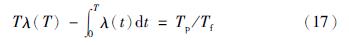
将服从3参数威布尔分布的机采井故障率函数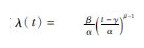 代入式(17),则得到最大可用度的预防检泵周期为
代入式(17),则得到最大可用度的预防检泵周期为
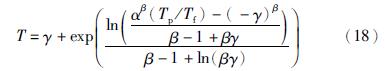
其中,α=378.731 5,β=1.619,γ=147.230 6.
3.2 模糊决策法确定最佳预防性检泵周期机采井最佳预防性检泵周期的确定方法有很多,在实际应用中,模糊决策法可以规范地分析评价含有模糊性因素的问题,适用于评价多因素综合的实际问题.
定义因素集U={u1,u2,u3},其中u1为安全性因素、 u2为经济性因素、 u3为最大可用度因素. 选定3位机采井设计人员、 3位机采井工程造价评估人员和4位具有10年机采井检泵经验的工人作为评分者: P={p1,p2,…,p10}. 以十分制对3种因素进行评分,定义评分集M={M(ui,pj)}(i=1,2,3; j=1,2,…,10),每位专家对于不同因素的评分记为M(ui,pj),计算每个因素的平均分数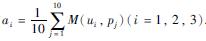 然后对a1,a2,a3做数据归一化处理,便可以得到3个影响因素对机采井最佳预防性检泵周期的影响权重A(ui)和模糊评价权重向量A={A(ui)}(i=1,2,3),其中
然后对a1,a2,a3做数据归一化处理,便可以得到3个影响因素对机采井最佳预防性检泵周期的影响权重A(ui)和模糊评价权重向量A={A(ui)}(i=1,2,3),其中 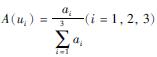 将3个因素单独计算得到的预防性检泵周期Ti乘以其影响权重A(ui),再求和得到模糊评价结果,即机采井最佳预防性检泵周期
将3个因素单独计算得到的预防性检泵周期Ti乘以其影响权重A(ui),再求和得到模糊评价结果,即机采井最佳预防性检泵周期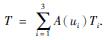
对于安全性因素,10位专家全都评满分10分,即M(u1,pj)=10,(j=1,2,…,10);
对于经济性因素,10位专家评分结果为
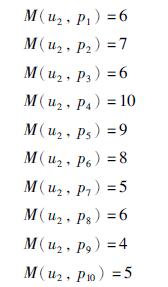
对于可用度最大因素,10位专家评分结果为
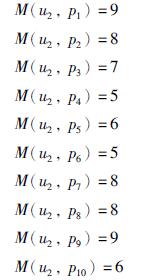
根据评分结果分别计算出3个因素的平均分为
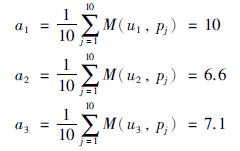
对3个因素平均分进行数据归一化,得到每个因素的影响权重为
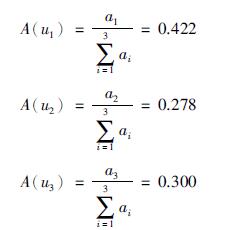
按照式(10)、 式(15)和式(18)分别计算出3个因素的预防性检泵周期为: T1=497.884 4 d,T2=279.403 1 d,T3=304.715 5 d. 机采井最佳预防性检泵周期为: T=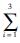 A(ui)Ti=379.195 9 d.
A(ui)Ti=379.195 9 d.
在复杂设备检修策略的发展过程中,预防性检修一直都是最重要的,起着主导作用. 合理的预防性检修策略可以提高机采井的可靠度,降低其故障发生率.
4.1 现有机采井检泵策略分析目前,在机采井实际检泵中,根据检泵的措施不同(更换故障部件和修复故障部件),将预防性检泵分成两类: 修复性预防检泵和更换性预防检泵.
4.1.1 修复性预防检泵修复性预防检泵时间图如图 6所示,其中T为预防性检泵周期、 Tp为预防性检泵时间、 Tf为故障检修时间. 由图 6可知,当机采井工作到预防性检泵周期T时,进行预防性检泵. 但如在一段时间T1(T1<T)内发生故障,修复发生故障的部件,使机采井恢复到故障前的采油状态,此时预防性检泵周期T=T1+T2,且继续工作T2时间后,进行预防性检泵.
 |
| 图 6 机采井修复性预防检泵时间图Fig. 6 Repairable preventive pump inspection time chart of the pump recovery well |
更换性预防检泵时间图如图 7所示,其中为预防性检泵周期、 Tp为预防性检泵时间、 Tf为故障检修时间. 由图 7可知,机采井如果在预防性检泵周期内没有发生故障,则等待机采井工作到预防性检泵周期进行预防性检泵. 如在一段时间T1(T1<T)内发生故障,需要对发生故障的部件进行更换,更换部件后机采井恢复到机采井初始的采油状态. 此时机采井预防性检泵周期清零,并将更换时刻作为周期的起点时间,直到机采井采油工作T时间后,进行预防性检泵.
 |
| 图 7 机采井更换性预防检泵时间图Fig. 7 Replaceable preventive pump inspection time chart of the pump recovery well |
根据确定的机采井最佳预防性检泵周期,并考虑机采井结构的复杂性和部件的昂贵性,将机采井发生的故障分为两类: 需更换部件的故障和可修复部件的故障. 制定最佳预防性检泵周期380 d的最佳预防性检泵策略,将其分为两部分,一是上述两类故障不同时出现在一个最佳预防性检泵周期,即单独检泵策略; 二是上述两类故障同时出现在一个最佳预防性检泵周期,即混合检泵策略.
4.2.1 机采井单独检泵策略机采井单独检泵策略时间图如图 8所示,其中T为机采井预防性检泵周期且T=T1+T2,Tp为预防性检泵时间,Tf为修复检泵时间,Te为更换检泵时间.
 |
| 图 8 机采井单独检泵策略时间图Fig. 8 Single pump inspection strategy time chart of the pump recovery well |
在T内如果没有发生任何故障,则到达T后进行预防性检泵; 经T1(T1<T)时间后,如果发生部件可修复故障,则进行修复性检泵操作,修复该部件后机采井正常工作,经T2(T2=T-T1)时间后,对机采井进行下一次预防性检泵; 如果某一时刻发生需更换部件故障,则进行更换性检泵操作,更换新的部件后使机采井正常工作, T清零,将此时刻作为T的起点. 机采井工作T时间后,进行预防性检泵.
4.2.2 机采井混合检泵策略机采井混合检泵策略时间图如图 9所示,其中T为机采井预防性检泵周期、 Tp为预防性检泵时间、 Tf为修复检泵时间、 Te为更换检泵时间.
 |
| 图 9 机采井混合检泵策略时间图Fig. 9 Mixed pump inspection strategy time chart of the pump recovery well |
在T内如果没有发生任何故障,则T时间后进行预防性检泵; 经T1(T1<T)时间后,如发生部件可修复故障,则进行修复性检泵操作,修复后机采井正常工作; 经T2(T2<T-T1)时间后,如出现需更换部件故障,则进行更换性检泵操作,更换后机采井正常工作,T清零,将此时刻作为T的起点. 机采井工作T(T>T1+T2)时间后,进行下一次预防性检泵.
4.3 机采井预防性检泵策略的对比分析在最佳预防性检泵周期的基础上确定最佳预防性检泵策略,将机采井的故障类别分为需更换部件故障和可修复部件故障. 根据两类故障给出机采井单独检泵策略和机采井混合检泵策略,使预防性检泵策略更具系统性和实用性.
根据上述分析,最佳预防性检泵策略比现有检泵策略具有以下几点优势:
(1) 通过模糊分析法得出最佳预防性检泵周期,并将其作为最佳预防性检泵策略的确定基础,更具科学性和合理性;
(2) 根据机采井故障类别及发生情况,将最佳预防性检泵策略分为单独检泵策略和混合检泵策略,更具综合性;
(3) 结合现有的检泵策略和检泵经验,系统地给出不同检泵策略的预防性检泵周期计算方法,更具实用性.
5 结论本文首先对机采井检泵周期数据进行威布尔分布建模分析,假设机采井检泵周期服从威布尔分布,并运用基于FPSO-SA算法的相关系数法对威布尔分布的3个参数进行估计; 然后运用K-S检验法做假设检验,从而验证机采井检泵周期服从威布尔分布,进而确定机采井故障率函数. 根据不同的实际因素定性分析机采井的预防性检泵周期,并通过应用模糊决策法确定机采井最佳预防性检泵周期,最后根据得到的最佳预防性检泵周期以及现有油田机采井的检泵策略,研究和确定机采井的最佳预防性检泵策略. 最佳预防性检泵周期和最佳预防性检泵策略对于机采井的检泵具有实际的应用价值.
| [1] | 马纪明, 万蔚, 曾声奎. 基于浴盆曲线故障率函数的FFOP预计方法[J]. 航空学报, 2012, 33(9): 1664-1670. Ma J M, Wan W, Zeng S K. FFOP prediction method based on bathtub-shaped failure rate function[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(9): 1664-1670. |
| [2] | 鹿鸣明. 油浸式变压器故障率模型及故障诊断研究[D]. 杭州: 浙江大学, 2014. Lu M M. Failure rate model and fault diagnose of oil-immersed transformers[D]. Hongzhou: Zhejiang University, 2014. |
| [3] | 鹿鸣明, 王逸飞, 郭创新, 等. 一种基于PHM考虑老化和设备状态的油浸式变压器故障率模型[J]. 电力系统保护与控制, 2014, 42(18): 66-71. Lu M M, Wang Y F, Guo C X, et al. Failure rate model for oil-immersed transformer based on PHM concerning aging process and equipment inspection information[J]. Power System Protection and Control, 2014, 42(18): 66-71. |
| [4] | 杨毅. 基于故障率特性的数控机床预防维修决策技术研究[D]. 重庆: 重庆大学, 2013. Yang Y. Study on preventive maintenance decision technology of CNC machine tools based on performance of fault rate[D]. Chongqing: Chongqing University, 2013. |
| [5] | Silva R B, Barreto-Souza W, Cordeiro G M, et al. A new distribution with decreasing, increasing and upside-down bathtub failure rate[J]. Computational Statistics and Data Analysis, 2010, 54(4): 935-944. |
| [6] | Xie M, Tang Y, Goh T N. A modified Weibull extension with bathtub-shaped failure rate function[J]. Reliability Engineering and System Safety, 2002, 76(3): 279-285. |
| [7] | Savsar M. Reliability analysis of a flexible manufacturing cell[J]. Reliability Engineering & System Safety, 2000, 67(2): 147-152. |
| [8] | 张志华. 可靠性理论及工程应用[M]. 北京: 科学出版社, 2012. Zhang Z H. Reliability theory and engineering application[M]. Beijing: Science Press, 2012. |
| [9] | 陈传海. 面向可靠性概率设计的数控机床载荷谱建立方法研究[D]. 吉林: 吉林大学, 2013Chen C H. Study on load spectrum for probability-reliability design of NC machine tools[D]. Jilin: Jilin University, 2013. |
| [10] | 张英芝, 申桂香, 吴甦, 等. 随机截尾数控机床三参数威布尔分布模型[J]. 吉林大学学报工学版, 2009, 39(2): 378-381. Zhang Y Z, Shen G X, Wu S, et al. 3-parameter Weibull distribution for random truncated NC machine tool fault data[J]. Journal of Jilin University Engineering and Technology Edition, 2009, 39(2): 378-381. |
| [11] | 薛玉霞, 申桂香, 张英芝, 等. 基于粒子群优化理论的可靠性分布模型的极大似然参数估计法[J]. 吉利大学学报: 工学版, 2009, 39(S1): 219-221. Xue Y X, Shen G X, Zhang Y Z, et al. Maximum likelihood method for parameter estimation of reliability distribution model based on particle swarm optimization theory[J]. Journal of Jilin University: Engineering and Technology Edition, 2009, 39(S1): 219-221. |
| [12] | Krink T, Vesterstrom J S, Riget J. Particle swam optimization with spatial particle extension[C]//Proceedings of the 2002 Congress on Evolutionary Computation. Piscataway, NJ, USA: IEEE, 2002: 1474-1497. |
| [13] | Xie X F, Zhang W J, Yang Z L. A dissipative particle swam optimization[C]//Proceedings of the IEEE International Conference on Evolutionary Computation. Piscataway, NJ, USA: IEEE, 2002: 1456-1461. |
| [14] | Higashi N, Iba H. Particle swarm optimization with Gaussian mutation[C]//Proceedings of the 2003 IEEE Swam Intelligence SymPois. Piscataway, NJ, USA: IEEE, 2003: 72-79. |
| [15] | 王琼, 王磊, 任伟建. 基于FPSO-SA算法的威布尔分布参数估计研究[J]. 吉林大学学报: 信息科学版, 2014, 32(5): 476-483. Wang Q, Wang L, Ren W J. Research on estimating parameters of Weibull distribution model based on FPSO-SA[J]. Journal of Jilin University: Information Science Edition, 2014, 32(5): 476-483. |
| [16] | Wang Z X, Chen Z S. Comparative analysis on the parameter estimation methods of Weibull distribution of extreme wave heights[J]. Marine Science Bulletin, 2013, 32(2): 127-132. |
| [17] | Dong S, Han Y, Tao S S, et al. Parameters estimation for Weibull distribution with particle swarm optimazition[J]. Periodical of Ocean University of China, 2012, 42(6): 120-125. |
| [18] | Luo H, Wang H J, Huang J G, et al. Method of united estimation to the parameters of three-parameter Weibull distribution based on PSO[J]. Chinese Journal of Scientific Instrument, 2009, 30(8): 1604-1612. |
| [19] | Pan H, Zhang X Y, Wu Y M. Applied statistics[M]. Beijing: People's Posts and Telecommunications Press, 2011. |
| [20] | Nan B. Statistical analysis of snow load based on K-S inspection method[J]. Journal of Lanzhou University of Technology, 2012, 38(1): 115-119. |



