求解双层应急物资调度的改进蜂群算法

文章快速检索

引用本文

宋晓宇, 张卿, 常春光. 求解双层应急物资调度的改进蜂群算法[J]. 信息与控制, 2015, 44(6): 729-738 复制到剪切板

SONG Xiaoyu, ZHANG Qing, CHANG Chunguang. Improved Bee Colony Algorithm for Solving Double Layer Emergency Resource Scheduling[J]. INFORMATION AND CONTROL, 2015, 44(6): 729-738. 复制到剪切板

求解双层应急物资调度的改进蜂群算法

宋晓宇¹, 张卿¹, 常春光²

1. 沈阳建筑大学信息与控制工程学院, 辽宁沈阳 110168;
2. 沈阳建筑大学管理学院, 辽宁沈阳 110168

收稿日期: 2014-09-23; 录用日期: 2014-12-11; 修回日期: 2015-02-03

基金项目:国家科技支撑计划资助项目（2006BAJ06B08-03）；教育部人文社会科学研究规划基金资助项目（2015-1274）；辽宁省自然科学基金资助项目（2015-604）.

作者简介: 宋晓宇（1963-），男，博士，教授.研究领域为应急管理，计算智能，模式识别，数据挖掘等.
张卿（1989-），女，硕士生.研究领域为应急管理，计算智能.
常春光（1973-），男，博士，教授.研究领域为应急管理，计算智能.

通讯作者:宋晓宇，sxy@sjzu.edu.cn

摘要：目前大多数的应急调度模型多以一层出救点来建立，而现实应急物资调度中，出救点不仅仅只有一层，而存在双层甚至是多层. 本文以非线性连续供给与消耗应急物资调度为背景，以物资调度总成本最小和整体反应时间最早为目标，建立由受灾点、分配中心和储备库组成的双层应急物资调度模型. 针对多目标多层级之间联动的应急物资调度模型的特点，采用基于反向学习策略和广泛学习策略的改进人工蜂群算法，得到Pareto最优解集，并分析Pareto前沿解集中解的个数与均匀性测度. 通过仿真实验验证了该模型的合理性和算法的有效性，实验结果表明该算法只需较少的成本和较早整体反应时间.

关键词：非线性连续供给与消耗双层应急物资调度人工蜂群算法反向学习广泛学习

Improved Bee Colony Algorithm for Solving Double Layer Emergency Resource Scheduling

SONG Xiaoyu¹ , ZHANG Qing¹ , CHANG Chunguang²

1. School of Information and Control Engineering, Shenyang Jianzhu University, Shenyang 110168, China;
2. School of Management, Shenyang Jianzhu University, Shenyang 110168, China

Abstract:At present, most emergency scheduling models are constructed on single-layer rescue points, but these points may double or even become multilayer rescue points in actual emergency resource scheduling. Based on nonlinear continuous supply and consumption of emergency resource scheduling, we developed an emergency resource scheduling model with two layers of affected points, i.e., distribution centers and reserve bases, to minimize total cost and reaction times. Based on the characteristics of multi-targets and multi-layers of the emergency resource scheduling model, our improved artificial bee colony algorithm uses opposition-based and comprehensive learning concepts to obtain Pareto-optimal solution sets and then analyzes the number of solutions for a Pareto front and uniformity measure. The simulation results show the model to be reasonable and the algorithm to be effective. Therefore, the proposed algorithm can minimize costs and achieve quicker overall reaction times.

nonlinear continuous supply and consumption double layer emergency resources scheduling artificial bee colony algorithm opposition-based learning comprehensive learning

1 引言

近年来，全球发生了多起重大自然灾害，从2008年的汶川地震、 2010年的玉树地震、 2011年的日本福岛地震到2014年的云南鲁甸地震. 为了降低自然灾害带来的后续损失，建立有效的应急物资调度方案显得尤为重要.

对于应急物资调度模型和智能优化算法领域已有大量相关研究，针对受灾点和出救点的数量，文[1, 2]将应急物资调度问题从单受灾点推广到多受灾点，并建立多出救点的应急物资调度模型，实现单资源到多资源的调度模型研究. 文[3, 4, 5]针对连续消耗应急物资调度问题，建立多资源的应急物资调度模型，实现应急物资一次性消耗向连续性消耗的转变. 文[6]建立应急物资在多目标多阶段条件下的组合优化模型. 文[7]根据每一个阶段变化的物资需求，建立以运输时间为目标的多阶段应急物资分配动态模型. 在智能优化算法方面，文[8, 9]将人工蜂群算法应用到车间和作业调度优化问题上. 文[10, 11, 12, 13, 14]提出人工蜂群算法，通过与其它智能算法对比来研究该算法的性能. 文[15, 16, 17]提出外部档案和Pareto支配概念并使用拥挤距离来保证外部档案中解的合理分布，同时采用广泛学习策略使算法能够找到更均匀的解. 文[18, 19]提出基于Pareto的多目标优化问题和使用非支配解排序的多目标进化算法. 文[20]在DE(differential evolution)算法初始解的产生和寻优过程中加入反向学习策略，经过实验验证反向学习策略使算法在收敛速度和求解精度上有很大提高.

本文从应急物资非线性连续消耗的实际出发，根据受灾点消耗速度曲线将整个救援过程划分为3个阶段，建立多受灾点和多出救点的多目标双层应急物资调度模型. 模型以物资调度总费用最小化和整体最早反应时间最小化为优化目标，不仅考虑节省物资调度费用，还对起始救援时间进行优化，使得模型更具有实际意义. 根据人工蜂群算法的优势与不足，将反向学习策略、广泛学习策略与人工蜂群算法相结合，提出一种基于Pareto支配的多目标人工蜂群(multi-objective artificial bee colony，MOABC)算法用于求解多目标应急物资调度问题. 仿真实验证明，本文提出的模型合理，多目标人工蜂群算法是一种求解多目标应急物资调度问题的有效方法.

2 应急调度模型建立 2.1 问题描述

非线性连续供给与消耗下的双层应急调度问题模型描述如下：假定A_j为受灾点，B_i为分配中心，C_q为储备库. 从自然灾害发生开始时刻到分配中心送达物资的理想时刻T₀(即待反应时刻)期间所造成的损失是不可避免的，假定这一阶段为第0阶段. 根据受灾点A_j的消耗速度曲线划分为3个独立曲线，即将受灾点A_j的消耗过程平均划分为3部分： [t_j⁽ⁱ⁾，T₁]为救援前期(第Ⅰ阶段)、 [T₁，T₂]为救援中期(第Ⅱ阶段)和[T₂，T]为救援后期(第Ⅲ阶段)，这3个阶段受灾点A_j的消耗速度曲线分别为v_j⁽¹⁾(t)=lb(t+1)、和每个阶段的开始时刻与结束时刻即为分配中心B_i为受灾点A_j供应物资的起始时刻与结束时刻，各阶段之间转换的时间忽略不计. 实时判断分配中心的实时库存量是否低于其临界库存量，若低于临界库存量，则储备库C_q开始为分配中心B_i供应物资，阶段结束时刻即储备库C_q供应物资结束时刻.

2.2 模型变量符号说明

A_j、 B_i和C_q分别为第j个受灾点(j=1，2，…，n)、第i个分配中心(i=1，2，…，m)和第q个储备库(q=1，2，…，w)；

v_j^(k)(t)和K分别为受灾点A_j在第k个阶段物资消耗速度，即单位时间内受灾点A_j的消耗物资量和阶段数；

v_i ^(j)(t)和v_q⁽ⁱ⁾(t)分别为单位时间内分配中心B_i向受灾点A_j供应物资量和单位时间内储备库C_q向分配中心B_i供应物资量；

Q_A₀^(j)、 Q_B₀⁽ⁱ⁾和Q_C₀^(q)分别为受灾点A_j的最大库存量、分配中心B_i的最大库存量和储备库C_q的最大库存量，且储备库物资量充足；

E_{A_j}^(k)和E_{B_i}^(k)分别为第k阶段，受灾点A_j的物资超额量和分配中心B_i的物资超额量；

L_j^(k)为第k阶段受灾点A_j的物资缺失量；

I_i^(k)(t_j⁽ⁱ⁾)和I₀⁽ⁱ⁾分别为第k阶段，分配中心B_i在阶段开始时刻的库存量和分配中心B_i的临界库存量；

c_ij和c_qi分别为分配中心B_i向受灾点A_j运送物资的单价和储备库C_q向分配中心B_i运送物资的单价；

e_A、 e_B和l分别为受灾点A_j单位物资超额费用、分配中心B_i单位物资超额费用和受灾点单位物资缺失费用；

S_ij^(k)和S_qj^(k)分别为第k阶段，分配中心B_i向受灾点A_j和储备库C_q向分配中心B_i供应物资的数量；

t_j⁽ⁱ⁾和t_qi^(k)分别为分配中心向受灾点运送物资的起始时刻即第Ⅰ阶段开始时刻和第k阶段储备库C_q向分配中心B_i运送物资起始时刻；

t_j^(E_k)、 t_j^(L_k)和t_i^(F_k)分别为第k阶段，受灾点A_j物资超额临界时刻、受灾点A_j物资缺失临界时刻和分配中心B_i物资超额临界时刻；

T₀、 T₁、 T₂和T分别为待反应时刻即B_i理想供给时刻、第Ⅰ阶段结束时刻、第Ⅱ阶段结束时刻和救援活动结束时刻.

2.3 模型建立

根据上节的问题描述，建立非线性连续供给与消耗的应急物资调度的数学模型如下：

其中，式(1)表示应急物资调度的总费用Z，包括3部分：第1部分是分配中心向受灾点和储备库向分配中心供应物资的成本费用；第2部分是超出受灾点最大库存量和超出分配中心最大库存量所产生的超额费用之和；第3部分是受灾点物资缺失导致的缺失费用. 式(2)表示分配中心向受灾点供应物资的整体最早反应时间. 式(3)表示从总量上来看，分配中心和储备库的最大库存量应满足整个救灾活动中受灾点的总物资消耗量. 式(4)引入0-1判断变量表示一个分配中心只能给一个受灾点供应物资. 式(5)引入0-1判断变量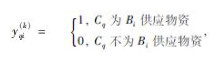表示一个储备库只能给一个分配中心供应物资. 式(6)表示当B_i的库存量小于等于其临界库存量时，存在时刻t_qi^(k)，t_qi^(k)∈[t_j⁽ⁱ⁾，T)使得储备库C_q开始向分配中心B_i供应物资. 式(7)表示分配中心B_i不允许出现物资缺失. 式(8)表示分配中心B_i向受灾点A_j供应物资的起始反应时间范围.

每个阶段的应急物资调度是以前一阶段的结果为基础，由于应急物资有供应时刻的限制，应急物资调度未必能够保障受灾点在任一阶段的非线性连续消耗，因此会出现物资部分缺失，甚至完全缺失. 在第0阶段，由于物资供给不及时，受灾点A_j存在物资缺失，则A_j在此时的物资消耗累计量，即物资需求量为物资缺失费用为由此得知在此阶段受灾点A_j不存在物资超额情况，即不产生超额费用，分配中心B_i不能给受灾点A_j供应物资，即A_j的物资消耗停止，分配中心B_i优先补偿第0阶段受灾点A_j的缺失物资. 根据第Ⅰ阶段物资消耗情况将整个救援过程分为3类：物资完全缺失型、物资部分缺失型和物资供应充足型，并分别分析第Ⅱ、 Ⅲ阶段物资消耗情况，共分为10种类型，如图 1所示.

图 1 应急调度模型分类Fig. 1 Emergency dispatch model classification

图选项

3 多目标人工蜂群算法设计 3.1 算法思想

以基本人工蜂群算法为基础，通过Pareto支配^[15]的概念比较解的优劣，并采用外部档案来保存Pareto中的非劣个体. 外部档案中所有解都看作是食物源的位置，使用带约束的Pareto支配关系更新最佳个体位置，当人工蜂群完成当代的搜索后，采用拥挤距离判断机制来维护外部档案解的分布. 由于初始种群的质量能够直接或间接地影响算法的寻优，本文采用随机均匀策略产生初始种群，采用反向学习策略进化初始种群，然后在当前的种群和进化后的种群中进行选择，保留较好种群. 为了更好地平衡ABC(artificial bee colony)算法的“探索”与“开发”的能力，在算法寻优阶段加入广泛学习策略^[16]和反向学习策略^[19]，目的是维持种群的多样性，提高算法搜索效率.

3.2 多目标人工蜂群算法 3.2.1 外部档案的更新

多目标问题在多个目标之间存在权衡问题，存在多个解，所以多目标问题的解是一个解集，而这个解集即为Pareto解集. 为了把应急调度模型中的约束加到算法中，在一般Pareto支配关系的基础上定义带约束的Pareto支配关系，如果下列情况之一成立，则认为个体x_i约束支配个体x_j：

(1)个体x_i是可行解，但个体x_j不可行；

(2)个体x_i和个体x_j均可行，但个体x_i按照一般Pareto支配关系要优于个体x_j；

(3)个体x_i和个体x_j均不是当前最优解，但个体x_i按照一般Pareto支配关系要优于个体x_j.

外部档案随着算法的迭代在每一代都进行更新. 每一个新解都需要与外部档案中非支配解进行比较以决定这个新解是否可以留在外部档案中. 随着算法的进化，越来越多的解将进入外部档案，算法运行时间会随着比较次数的增加而增加，因此必须对外部档案的大小加以限定. 完成当代搜索后会产生新解，如果有新解进入外部档案，需要更新，同时检查外部档案中是否有重复的解，如果有则只保留一个；如果外部档案中的非支配解的个数n没有达到外部档案的最大容量N，则进行下一代搜索；若当外部档案中非支配解的个数n超出了外部档案所能容纳解的数量N，则拥挤距离将会作为一个度量来移除外部档案中过于拥挤的成员，同时维持外部档案中解的良好分布.

3.2.2 广泛学习策略

ABC算法在单目标优化领域里已被证实具有优异的优化性能. 但新解的产生仍旧采用原来的策略只在1个维度上进行更新，显然产生更优解的概率会很低，这样将极大地影响算法的收敛速度. 因此为了使ABC算法能更好地应用于多目标优化问题，加入广泛学习策略，以扩展算法求解的多样性.

每次迭代中，蜜蜂随机选择一个食物源位置，对应当前食物源随机生成随机数r，r∈[0, 1]，广泛学习概率为J_s. 若r≤J_s则采用广泛学习策略产生新解v_i，每个蜜蜂x_i随机挑选m个维度向其在外部档案EA中随机选择非支配解x_k进行学习. 同时其他每一个维度随机向外部档案中其它非支配解x_l所对应的维度学习^[15]. 根据式(14)，x_i的m维向x_k的m维学习，其它维度根据式(15)进行学习：

式(14)中，EA_k是外部档案中第k个解，k∈{1，2，…，n}是随机选择的索引，n是当前外部档案中支配解的个数； f(m)决定x_i中哪些维度向EA_k学习； φ(m)产生m个^{[0, 2]}之间的随机数，且这m个随机数与上述m相对应. 式(15)中，φ_ij是[0, 1]之间的随机数，l≠k，j∈{1，2，…，n}，j

f(m). 产生的新解v_i与原解进行比较，根据Pareto约束决定其是否可以进入外部档案中. 如果新解v_i不被原解所支配，则v_i可以进入外部档案中；否则不允许放入外部档案中.

3.2.3 反向学习策略

标准的群搜索优化算法在处理问题时易陷入局部最优，在优化后期收敛速度明显变慢，甚至处于停滞状态，难以获得较好的全局最优解. 由于ABC算法随机产生初始种群，这样的随机猜测值作为初始种群对算法的影响很大. 若随机猜测值离最优解很近，算法也许能很快地收敛；相反则会耗费很多时间. 所以在搜索过程中，同时搜索当前解和反向解，选择较好的解作为猜测解，则会大大提高算法的效率. 本文在种群初始化时采用反向学习策略，而在蜜蜂觅食阶段则按照一定的学习概率进行反向学习. 一般反向学习策略中反向数(opposite number)^[19]的定义为：若x∈[a，b]且x∈R，则其反向数x^*为x^*=a+b-x. 本文将反向数进行如下改变：将分配中心B_i向受灾点A_j供应物资的速度v_i(t)进行反向，即：

式中，v为当前速度的平均数， v′_i(t)为当前速度v_i(t)的反向数. 反向数具体情况为

(1)当v_i(t)>v，则v′_i(t)=v_i(t)-2Δ；

(2)当v_i(t)<v，则v′_i(t)=v_i(t)+2Δ；

(3)当v_i(t)=v，则v′_i(t)=v_i(t)；

(4)若v′_i(t)<LL，则取v′_i(t)=LL；

(5)若v′_i(t)>UL，则取v′_i(t)=UL.

其中，Δ为反向距离，即当前速度与平均速度差，LL和UL分别为速度的下限值和上限值.

3.2.4 拥挤距离的计算

为了估计外部档案中一个个体周围其它个体的密集程度，需要计算个体的拥挤距离d_i ，计算步骤如下：

(1) 初始化外部档案中每个个体的拥挤距离d_i=0；

(2) 外部档案中的个体分别将对应的目标函数值Z_i和τ_i进行归一化，将归一化后的目标函数值的大小升序排列，归一化公式如下：

(3) 排序后，边界个体的拥挤距离设为无穷大，其余个体的拥挤距离的具体计算公式如下：

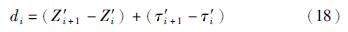
其中，Z′_i、 Z′_i+1、 τ′_i和τ′_i+1为归一化后个体目标函数值，且均在[0, 1]之间； Z_max和τ_max为当前外部档案中两个目标函数的最大值. 计算可知拥挤距离越小，个体越密集，解的多样性越差；反之说明个体越稀疏，多样性越好，从而维持外部档案中解的一个良好分布.

3.3 算法步骤

基于以上算法思想的描述，多目标人工蜂群算法步骤如下：

步骤1：完成算法相关参数的设置，随机生成供给关系并产生初始解，基于反向学习策略得到一组反向种群，根据适应度值对当前种群与反向种群进行精英选择，得到新的种群，即初始解x_i(i=1，2，…，S₀)，评价种群中的所有个体.

步骤2：根据Pareto支配关系筛选出初始解中的非劣个体，用于初始化外部档案.

步骤3：引领蜂阶段：每一个引领蜂对应一个食物源，并对食物源x_i进行一次邻域搜索，同时对应当前食物源随机生成[0, 1]之间的随机数r. 若r∈[0，J_s]，则采用广泛学习策略产生新解v_i；否则采用随机学习策略产生新食物源. 计算v_i的适应度值，并与原解进行比较，根据贪婪算法选择较好的一个作为其对应的食物源位置，结束对引领蜂的处理. 同时根据Pareto支配关系比较新解与原解，决定新解是否进入外部档案. 若超出设定的外部档案容量时，则根据拥挤距离来排除过于拥挤的解.

步骤4：计算每个食物源被选择的概率p_i.

步骤5：跟随蜂阶段：对每个跟随蜂进行处理. 根据p_i选择一个食物源的位置，同时对应当前食物源随机生成[0, 1]之间的随机数r. 若r∈[0，J_s]，则采用广泛学习策略产生一个新的食物源v_i；否则采用随机学习策略产生新食物源. 计算新食物源的适应度值，应用贪婪机制进行选择，结束对观察蜂的处理. 同时根据引领蜂阶段完成外部档案的更新.

步骤6：经过跟随蜂阶段得到新解，并生成[0, 1]之间与之对应的随机数r，反向学习概率为J_r，若r∈[0，J_r]，则采用反向学习策略产生新解. 对个体进行评价，完成外部档案更新.

步骤7：侦察蜂阶段：当一个食物源适应值经过l₀次循环之后没有得到改善，该食物源被抛弃，与之对应的引领蜂变为侦察蜂，并重新随机搜索一个新位置来代替原食物源，结束对侦察蜂的处理.

步骤8：未达到调用评价次数N₀次，则转到步骤3；若达到调用评价次数N₀次时，则停止算法.

步骤9：算法停止，输出外部档案，获得Pareto解集.

4 仿真算例

根据应急物资的需求特征，应急物资的消耗过程分为3阶段：初期，要求受灾点全面覆盖，物资消耗速度极大，容易出现物资供不应求；中期，救助对象相对确定，物资消耗量相对较大；后期，受灾点生产生活自理，物资消耗速度相对平稳. 为验证上述应急物资调度模型的合理性和算法的有效性，对该应急物资的调度过程进行仿真实验. 针对反向学习概率J_r、广泛学习概率J_s和种群大小M的取值对实验的影响进行分析，并对Pareto前沿解集中解的个数和解的均匀性进行分析和对比. 实验结果证明MOABC算法更加高效，为用户提供了更多解决方案的选择.

本文数据采用随机方法分别生成2种规模下每种10组应急物资调度问题的实验数据，具体数据随机生成范围如表 1所示.

表 1 2种规模实验数据随机生成规则Tab. 1 Randomly generated rules of two kinds of scale experimental data

	Q_A₀^(j)	Q_B₀⁽ⁱ⁾	I₀⁽ⁱ⁾	v_i(t)^(j)	v_q(t)⁽ⁱ⁾	t_j⁽ⁱ⁾	c_ij	c_qi
较小规模	[300， 400]	[300， 550]		[5， 20]	[5， 50]	[0， 50]	[0.10， 0.50]	[0.10， 0.40]
较大规模	[300， 500]	[300， 600]		[5， 20]	[5， 60]	[0， 50]	[0.10， 0.50]	[0.10， 0.40]

表选项

本文的实验结果都是通过Visual Studio 2010使用C++语言编程运行所得，本文算法的实验参数设置为：种群大小M为100，外部档案大小N为200，解被更新次数l₀为10，采用相同次数的调用评价次数N₀作为算法终止条件.

4.1 算例1

某地区有4个受灾点急需物资，并有4个分配中心为受灾点提供应急物资，受灾点和分配中心具体信息如表 2所示. 同时该周围还有4个储备库为分配中心提供应急物资，供需网络参数信息如表 3和表 4所示.

表 2 受灾点和分配中心信息Tab. 2 Information of the affected points and distribution centers

	A₁	A₂	A₃	A₄	B₁	B₂	B₃	B₄
Q_A₀^(j)/Q_B₀⁽ⁱ⁾	382	369	400	347	536	328	546	365
I_m⁽ⁱ⁾	-	-	-	-	179	109	182	122
T₀	1	1	1	1	-	-	-	-
T	900	900	900	900	-	-	-	-
l	10	10	10	10	-	-	-	-
e_A、 e_B	0.08	0.08	0.08	0.08	0.02	0.02	0.02	0.02

表选项

表 3 供需网络1参数信息Tab. 3 Parameters information of the supply and demand network 1

	A₁			A₂			A₃			A₄
	v_i⁽¹⁾(t)	t₁⁽ⁱ⁾	c_i1	v_i⁽²⁾(t)	t₂⁽ⁱ⁾	c_i2	v_i⁽³⁾(t)	t₃⁽ⁱ⁾	c_i3	v_i⁽⁴⁾(t)	t₄⁽ⁱ⁾	c_i4
B₁	5	45	0.10	15	23	0.19	10	7	0.48	18	9	0.45
B₂	7	26	0.15	19	5	0.48	5	42	0.35	10	10	0.40
B₃	5	25	0.30	14	11	0.45	17	12	0.40	6	40	0.22
B₄	20	2	0.50	11	9	0.41	16	14	0.20	14	17	0.34

表选项

表 4 供需网络2参数信息Tab. 4 Parameters information of the supply and demand network 2

	B₁		B₂		B₃		B₄
	v_q⁽¹⁾(t)	c_q1	v_q⁽²⁾(t)	c_q2	v_q⁽³⁾(t)	c_q3	v_q⁽⁴⁾(t)	c_q4
C₁	50	0.36	23	0.23	9	0.15	17	0.20
C₂	13	0.17	7	0.10	37	0.30	19	0.22
C₃	31	0.24	14	0.17	7	0.10	14	0.24
C₄	11	0.12	16	0.15	19	0.20	20	0.27

表选项

4.1.1 与标准人工蜂群算法对比

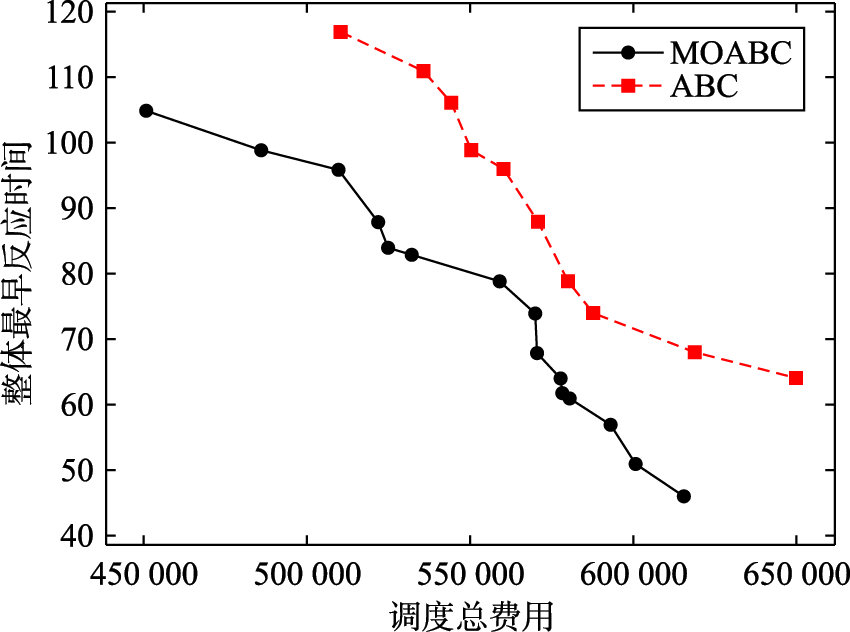
根据上述模型与算法，对较大规模应急物资调度过程进行实验，将MOABC算法和标准ABC算法进行对比得到Pareto前沿如图 2所示. 从中能够看到MOABC算法所得的解都是最优解，且Pareto前沿分布均匀. 任意两个调度方案之间在物资调度总费用和整体反映时间上不存在Pareto支配关系.

图 2 多目标人工蜂群算法Pareto解的分布Fig. 2 The distributions of Pareto solutions for multi-objective artificial bee colony algorithm

图选项

分析和对比MOABC算法和标准ABC算法结果，由表 5可知，最小整体反应时间由64 min降低为46 min，同比降低了28.13％；而所搜索到的最大整体反应时间由117 min降低为105 min，减少率为10.26％；同时平均整体反应时间降低了17.44％. 对于应急物资调度总成本，算法改进前、后Pareto前沿中最小总成本减少率为11.78％，最大总成本的减少率为5.35％，同理所得平均应急物资调度总成本由571 117.73元降低到551 203.81元，降低率为3.49％. 对于Pareto前沿中最优解的个数，算法改进后由改进前10个最优解增加到了15个最优解，并由图 2可知，算法改进后的任一方案在应急物资调度总费用和整体反应时间上都要优于算法改进前的方案.

表 5 MOABC算法与ABC算法数据结果对比Tab. 5 Comparison of data results between MOABC algorithm and ABC algorithm

	M	N₀	J_r	J_s	min τ_i/min	max τ_i/min	min Z	max Z	τ_i/min	Z	n_Pareto
MOABC	100	650 000	0.3	0.6	46	105	450 566.855	615 428.251	74.47	551 203.805	15
ABC	100	650 000	0	0	64	117	510 746.375	650 210.354	90.20	571 117.730	10

表选项

4.1.2 反向学习概率

根据上述模型与算法，在MOABC算法中只加入反向学习策略(ABC+OBL)，并针对反向学习概率J_r的取值进行以下实验对比：当反向学习概率J_r分别为0.4、 0.3、 0.2、 0.1和0.0时，对比结果如表 6所示.

表 6 不同J_r取值数据结果对比Tab. 6 Comparison of the results of data in different J_r

	M	N₀	J_s	min τ_i/min	max τ_i/min	min Z	max Z	τ_i/min	Z	n_Pareto
J_r=0.4	100	700 000	0	51	108	477 948.678	627 275.198	83.31	557 316.329	13
J_r=0.3	100	700 000	0	46	106	450 566.855	619 164.329	75.43	555 841.377	14
J_r=0.2	100	700 000	0	57	111	489 103.716	638 319.913	85.85	559 953.631	13
J_r=0.1	100	700 000	0	57	111	510 465.376	644 025.247	87.92	567 979.873	12
J_r=0.0	100	700 000	0	64	112	510 880.021	646 040.186	89.30	570 796.980	10

表选项

分析和对比不同J_r取值与未加入反向学习策略的ABC算法结果，由表 6可知，当J_r=0.3时得到最优解集. 最小整体反应时间降低了28.13％，最大整体反应时间降低5.36％，最小调度总费用减少11.81％，最大调度总费用减少4.16％. 同时所得平均整体反应时间降低了15.53％，所得平均应急物资调度总成本减少了2.62％. 对于所得到的Pareto解个数相对于未改进算法的Pareto解的个数增加了4个.

4.1.3 广泛学习概率

根据上述模型与算法，在实验4.1.2的基础上(J_r=0.3)加入广泛学习策略，并针对广泛学习概率J_s的取值进行以下实验对比：当广泛学习概率分别为0.3、 0.4、 0.5、 0.6和0.0时，对比结果如表 7所示.

表 7 不同J_s取值数据结果对比Tab. 7 Comparison of the results of data in different J_s

	M	N₀	J_r	min τ_i/min	max τ_i/min	min Z	max Z	τ_i/min	Z	n_Pareto
J_s=0.4	100	650 000	0.3	53	111	473 942.408	638 319.913	79.46	566 551.901	13
J_s=0.5	100	650 000	0.3	51	108	467 127.269	627 275.198	76.79	560 859.958	14
J_s=0.6	100	650 000	0.3	46	105	450 566.855	615 428.251	74.47	551 203.805	15
J_s=0.7	100	650 000	0.3	46	106	458 752.718	620 160.008	75.36	55 6762.948	14
J_s=0.0	100	650 000	0.3	57	112	479 245.292	644 025.247	81.00	569 765.770	12

表选项

基于实验5.1.2，分析和对比加入广泛学习策略后的算法，针对不同J_s取值与未加入广泛学习策略的实验5.1.3中算法的结果，由表 7可知，当J_s=0.6时得到最优解集. 最小整体反应时间降低了19.30％，最大整体反应时间降低了6.25％. 将调度总成本所得结果进行对比，最小调度总费用减少了5.98％，同时最大调度总费用降低了4.44％，并且所得平均整体反应时间降低了8.06％，所得平均应急物资调度总成本减少了3.26％. 对于搜索到的Pareto解的个数相对于未改进算法的Pareto解的个数增加了3个.

4.1.4 种群大小

针对上述模型与算法，使用MOABC算法(J_r=0.3、 J_s=0.6)对种群大小M进行讨论，实验对比如下，当M分别为50、 100和200时，数据结果对比如表 8所示.

表 8 不同M取值数据结果对比Tab. 8 Comparison of the results of data in different M

	N₀	J_r	J_s	min τ_i/min	max τ_i/min	min Z	max Z	τ_i/min	Z	n_Pareto
M=50	1 300 000	0.3	0.6	46	105	458 752.718	638 245.292	73.79	559 947.524	14
M=100	1 300 000	0.3	0.6	43	99	431 732.225	610 231.370	69.82	523 521.043	17
M=200	1 300 000	0.3	0.6	43	99	441 150.052	615 548.145	72.60	542 253.897	15

表选项

分析和对比针对应急物资调度模型的算法种群大小分别为50、 100和200的结果，由表 8可知，当M=100时得到Pareto最优解集，其最小整体反应时间为43 min，与之对应的最大调度总费用下降了4.39％；其最大整体反应时间减少5.71％，与之对应的最小调度总费用成本最低；平均整体反应时间减少了5.38％；平均调度总费用减少了6.51％； Pareto前沿中得到的最优解个数最多，同时，随着调用评价次数N₀由650 000增加到1 300 000，搜索到的Pareto最优解也由15个增加到了17个.

4.2 算例2

某地区有8个受灾点急需物资，并有8个分配中心为受灾点提供应急物资，受灾点和分配中心具体信息如表 9所示. 同时该周围还有8个储备库为分配中心提供应急物资，供需网络参数信息如表 10和表 11所示.

表 9 受灾点和分配中心信息Tab. 9 Information of the affected points and distribution centers

	A₁	A₂	A₃	A₄	A₅	A₆	A₇	A₈	B₁	B₂	B₃	B₄	B₅	B₆	B₇	B₈
Q_A₀^(j)/Q_B₀⁽ⁱ⁾	500	342	468	379	357	477	354	495	591	302	568	369	337	479	345	575
I_m⁽ⁱ⁾	-	-	-	-	-	-	-	-	302	100	189	123	112	159	115	191
T₀	1	1	1	1	1	1	1	1	-	-	-	-	-	-	-	-
T	900	900	900	900	900	900	900	900	-	-	-	-	-	-	-	-
l	10	10	10	10	10	10	10	10	-	-	-	-	-	-	-	-
e_A、 e_B	0.08	0.08	0.08	0.08	0.08	0.08	0.08	0.08	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.02

表选项

表 10 供需网络1参数信息Tab. 10 Parameters information of the supply and demand network 1

	A₁			A₂			A₃			A₄			A₅			A₆			A₇			A₈
	v_i⁽¹⁾(t)	t₁⁽ⁱ⁾	c_i1	v_i⁽²⁾(t)	t₂⁽ⁱ⁾	c_i2	v_i⁽³⁾(t)	t₃⁽ⁱ⁾	c_i3	v_i⁽⁴⁾(t)	t₄⁽ⁱ⁾	c_i4	v_i⁽⁵⁾(t)	t₅⁽ⁱ⁾	c_i5	v_i⁽⁶⁾(t)	t₆⁽ⁱ⁾	c_i6	v_i⁽⁷⁾(t)	t₇⁽ⁱ⁾	c_i7	v_i⁽⁸⁾(t)	t₈⁽ⁱ⁾	c_i8
B₁	20	8	0.49	5	45	0.10	15	23	0.19	10	22	0.20	10	7	0.48	7	32	0.15	6	44	0.12	18	9	0.45
B₂	5	50	0.12	7	26	0.15	19	5	0.48	5	35	0.14	10	13	0.49	5	42	0.35	10	10	0.40	20	5	0.50
B₃	5	25	0.30	5	39	0.14	18	14	0.40	14	11	0.45	19	5	0.49	17	12	0.40	20	8	0.43	6	40	0.22
B₄	20	2	0.50	7	22	0.35	19	6	0.48	11	9	0.41	16	14	0.20	12	32	0.19	14	17	0.34	19	35	0.12
B₅	7	33	0.19	7	27	0.15	11	12	0.20	9	19	0.22	17	11	0.30	18	47	0.12	6	29	0.22	13	13	0.39
B₆	15	23	0.20	17	36	0.17	19	10	0.42	11	5	0.49	16	26	0.25	12	2	0.50	17	19	0.29	9	28	0.27
B₇	9	29	0.50	7	38	0.20	11	15	0.40	19	11	0.35	16	5	0.42	9	23	0.25	7	37	0.20	5	44	0.15
B₈	11	17	0.30	7	12	0.35	12	31	0.20	5	37	0.19	6	29	0.21	18	6	0.50	19	3	0.50	14	15	0.22

表选项

表 11 供需网络2参数信息Tab. 11 Parameters information of the supply and demand network 2

	B₈		B₁		B₂		B₃		B₄		B₅		B₆		B₇
	v_q⁽¹⁾(t)	c_q1	v_q⁽²⁾(t)	c_q2	v_q⁽³⁾(t)	c_q3	v_q⁽⁴⁾(t)	c_q4	v_q⁽⁵⁾(t)	c_q5	v_q⁽⁶⁾(t)	c_q6	v_q⁽⁷⁾(t)	c_q7	v_q⁽⁸⁾(t)	c_q8
C₁	9	0.10	54	0.15	6	0.30	23	0.10	11	0.20	9	0.15	17	0.21	40	0.21
C₂	10	0.12	20	0.10	15	0.13	47	0.22	14	0.14	8	0.15	19	0.10	37	0.20
C₃	33	0.14	22	0.10	9	0.11	27	0.21	7	0.22	36	0.13	11	0.10	49	0.15
C₄	13	0.17	31	0.10	19	0.18	12	0.31	45	0.22	14	0.15	77	0.13	20	0.12
C₅	12	0.12	16	0.15	13	0.10	7	0.30	19	0.20	17	0.21	5	0.10	15	0.23
C₆	19	0.11	12	0.21	7	0.14	9	0.10	16	0.13	17	0.17	11	0.11	15	0.23
C₇	11	0.15	10	0.30	7	0.14	15	0.20	12	0.15	17	0.21	14	0.24	16	0.10
C₈	17	0.21	6	0.12	16	0.24	19	0.30	18	0.10	7	0.17	9	0.18	5	0.13

表选项

根据上述模型，对应急物资调度过程进行测试，将MOABC算法和标准ABC算法进行对比得到Pareto前沿如图 3所示.

图 3 多目标人工蜂群算法Pareto解的分布Fig. 3 The distribution of Pareto solutions for MOABC algorithm

图选项

综上2个算例实验结果，针对本文非线性连续供给与消耗的双层应急物资调度模型特点，提出MOABC算法，由实验结果可知反向学习概率建议取值在[0.3，0.4]之间，广泛学习概率建议取值在[0.6，0.7]之间，初始种群大小建议取值在100左右. 实验结果证明加入广泛学习策略与反向学习策略后得到的Pareto解的个数得到了明显增加.

4.3 性能评价

对于多目标问题而言，分布均匀的非支配解集是优化的关键，为了更好地评价算法性能，本文从Pareto前沿解数量和Pareto前沿解均匀性测度指标两方面进行分析评价.

4.3.1 Pareto前沿解数量

Pareto前沿解的数量决定解的多样性，数量越多，解的多样性越好，针对应急调度实际问题为用户提供的调度方案就越多. ABC算法、 ABC+CL算法、 ABC+OBL算法和MOABC算法的Pareto前沿解的个数对比如表 12所示.

表 12 Pareto前沿解个数Tab. 12 The numbers of the Pareto front solutions

规模大小		4×4×4				8×8×8
算法		ABC	ABC+CL	ABC+OBL	MOABC	ABC	ABC+CL	ABC+OBL	MOABC
运行次数	1	8	10	12	14	10	13	19	20
	2	6	9	11	13	11	14	17	19
	3	8	9	10	15	9	10	15	20
	4	7	8	13	14	11	12	18	19
	5	10	11	14	13	12	15	19	18
	6	9	11	14	15	10	13	19	20
	7	9	10	11	14	11	14	16	19
	8	8	9	13	14	8	11	19	20
	9	10	11	13	15	11	13	18	19
	10	9	10	12	15	11	13	19	20
	平均	8.4	9.8	12.3	14.2	10.4	12.8	17.9	19.4

表选项

由表 12可知，在规模大小为4×4×4的应急调度问题的求解中，ABC+CL算法求解的Pareto前沿解个数提高了16.67％，ABC+OBL算法求解的Pareto前沿解个数提高了46.43％，而MOABC算法求解的Pareto前沿解个数提高了69.05％；在规模大小为8×8×8的应急调度问题的求解中，ABC+CL算法求解的Pareto前沿解个数提高了23.08％，ABC+OBL算法求解的Pareto前沿解个数提高了72.12％，而MOABC算法求解的Pareto前沿解个数提高了86.54％. 综上所述，本文提出的MOABC算法求解具有更好的多样性.

4.3.2 Pareto前沿解均匀性测度

对于多目标优化问题而言，Pareto前沿解的个数固然重要，但是Pareto前沿解的均匀性也很重要. 本文采用NSGAⅡ算法中定义的基于Pareto前沿解之间连续距离的评价指标Δ^[19]对算法所求出的Pareto前沿解分布的均匀程度进行分析，其值越小，说明其解分布越均匀. 为了更好地计算评价指标Δ，先将各个解的目标函数值(如式(19))进行归一化，评价指标Δ计算如式(20)所示. ABC算法、 ABC+CL算法、 ABC+OBL算法和MOABC算法的Pareto前沿解的均匀性测度结果如表 13所示.

表 13 Pareto前沿解集均匀性测度ΔTab. 13 The uniformity measure Δ of the Pareto front solutions

规模大小		4×4×4				8×8×8
算法		ABC	ABC+CL	ABC+OBL	MOABC	ABC	ABC+CL	ABC+OBL	MOABC
运行次数	1	0.158 922	0.113 161	0.058 512	0.022 154	0.139 065	0.116 330	0.078 425	0.023 175
	2	0.212 138	0.089 157	0.078 793	0.036 255	0.144 294	0.123 131	0.087 312	0.003 634
	3	0.156 860	0.132 073	0.121 321	0.005 252	0.180 122	0.112 612	0.100 168	0.026 663
	4	0.162 031	0.132 083	0.059 993	0.030 395	0.129 959	0.140 215	0.097 959	0.045 677
	5	0.209 924	0.161 085	0.013 787	0.013 057	0.154 159	0.114 376	0.091 099	0.029 989
	6	0.174 022	0.126 868	0.059 512	0.007 438	0.125 054	0.131 386	0.045 123	0.000 711
	7	0.123 424	0.103 641	0.056 913	0.010 638	0.119 830	0.106 366	0.064 751	0.011 054
	8	0.109 517	0.108 966	0.073 028	0.053 484	0.270 324	0.097 738	0.031 516	0.025 978
	9	0.151 937	0.143 511	0.169 843	0.012 868	0.120 403	0.100 323	0.010 868	0.015 306
	10	0.110 534	0.109 234	0.067 451	0.010 638	0.144 433	0.111 924	0.048 194	0.001 527
	平均	0.156 930 9	0.121 977 9	0.075 915 3	0.020 217 9	0.152 764 3	0.115 440 1	0.065 541 5	0.018 371 4

表选项

其中，f′₁和f′₂分别为目标函数f₁和目标函数f₂归一化后的值，f_1max和f_2max分别为目标函数f₁和目标函数f₂中的最大值.

其中，N₁为Pareto前沿解所得个数，d_i为在Pareto前沿解集上2个解的欧氏距离，d为这些欧氏距离的平均距离.

由表 13可知，在规模大小为4×4×4的应急调度问题的求解中，ABC+CL算法求解的Pareto前沿解集均匀性测度Δ指标降低了22.27％，ABC+OBL算法求解的Pareto前沿解集均匀性测度Δ指标降低了51.63％，MOABC算法求解的Pareto前沿解集均匀性测度Δ指标降低了87.12％；在规模大小为8×8×8的应急调度问题的求解中，ABC+CL算法求解的Pareto前沿解集均匀性测度Δ指标降低了24.43％，ABC+OBL算法求解的Pareto前沿解集均匀性测度Δ指标降低了57.10％，MOABC算法求解的Pareto前沿解集均匀性测度Δ指标降低了87.97％. 综上所述，本文提出的MOABC算法在Pareto前沿解集均匀性测度Δ方面也优于其它算法.

5 结论

本文从非线性连续供给与消耗的客观事实出发，根据受灾点的消耗速率曲线将整个过程划分为3个阶段，获得了较早的整体最早反应时间和较低的应急物资调度总成本. 通过实时判断分配中心的库存量与其临界库存量的关系，实现了双层应急物资调度之间的联动问题，具有较强的实际应用背景. 同时本文采用基于反向学习策略和广泛学习策略的多目标人工蜂群算法，更好地平衡了算法的“探索”与“开发”能力，并获得了较好的Pareto最优解集. 通过对Pareto前沿解集个数和均匀性指标的分析，得出MOABC算法求得的解更具有多样性，且Pareto前沿解更均匀. 实际应急物资调度问题中大量信息是不确定的，在不确定信息条件下非线性连续供给与消耗应急物资调度问题的研究将会是未来主要研究的方向之一.

参考文献

[1]	李进, 张江华, 朱道立. 灾害链中多资源应急调度模型与算法[J]. 系统工程理论与实践, 2011, 31(3): 488-495. Li J, Zhang J H, Zhu D L. Multi-resource emergency scheduling model and algorithm in disaster chain[J]. Systems Engineering-Theory & Practice, 2011, 31(3): 488-495.

[2]	刘春林, 何建敏, 盛昭瀚. 多出救点应急系统最优方案的选取[J]. 管理工程学报, 2000, 14(1): 13-15. Liu C L, He J M, Sheng Z H. Selection of optimal scheme for multi-depot emergency systems[J]. Journal of Industrial Engineering and Engineering Management, 2000, 14(1): 13-15.

[3]	潘郁, 余佳, 达庆利. 基于粒子群算法的连续性消耗应急资源调度[J]. 系统工程学报, 2007, 22(5): 556-560. Pan Y, Yu J, Da L Q. Emergency resources scheduling on continuous consumption system based on particle swarm optimization[J]. Journal of Systems Engineering, 2007, 22(5): 556-560.

[4]	柴秀荣, 王儒敬. 多出救点、多物资应急调度算法研究[J]. 计算机工程与应用, 2010, 46(6): 224-226. Chai X R, Wang R J. Research of emergent material dispatching algorithm based on multi-depot and multimaterial[J]. Computer Engineering and Applications, 2010, 46(6): 224-226.

[5]	宋晓宇, 王建国, 常春光. 基于需求紧迫度的非线性连续消耗应急调度模型与算法研究[J]. 信息与控制, 2014, 43(6): 735-743. Song X Y, Wang J G, Chang C G. Nonlinear continuous consumption emergency material dispatching model based on demand urgency degrees and its algorithm[J]. Information and Control, 2014, 43(6): 735-743.

[6]	陈兴, 王勇, 吴凌云, 等. 多阶段多目标多部门应急决策模型[J]. 系统工程理论与实践, 2010, 30(11): 1977-1985. Chen X, Wang Y, Wu L Y, et al. Emergency decision model with multiple stages, multiple objectives, and multidivisional cooperation[J]. Systems Engineering-Theory & Practice, 2010, 30(11): 1977-1985.

[7]	Ozdamar L, Ekinci E, Kucukyazici B. Emergency logistics planning in natural disasters[J]. Annals of Operation Research, 2004, 129(1/2/3/4): 217-245.

[8]	周刚. 基于人工蜂群算法的柔性调度问题研究[D]. 北京: 清华大学, 2012. Zhou G. Research on flexible scheduling problems based on artificial bee colony algorithm[D]. Beijing: Tsinghua University, 2012.

[9]	杨海军. 云计算环境下人工蜂群作业调度算法设计[J]. 数学的实践与认识, 2012, 42(10): 115-120. Yang H J. A job scheduling algorithm based on artificial bee colony in cloud computing[J]. Mathematics in Practice and Theory, 2012, 42(10): 115-120.

[10]	Karaboga D. An idea based on honey bee swarm for numerical optimization[R]. Kayseri, Turkey: Erciyes University, 2005.

[11]	Karaboga D, Basturk B. On the performance of artificial bee colony (ABC) algorithm[J]. Applied Soft Computing, 2008, 8(2): 687-697.

[12]	Baykasoglu A, Ozbakir L, Tapkan P. Artificial bee colony algorithm and its application to generalized assignment problem[M]//Swarm Intelligence: Focus on Ant and Particle Swarm Optimization. Vienna, Austria: I-Tech Education and Publishing, 2007, 113-144.

[13]	Vural R A, Yildirm T, Kadioglu T, et al. Performance evaluation of evolutionary algorithms for optimal filter design[J]. IEEE Transactions on Evolutionary Computation, 2012, 16(1): 135-147.

[14]	高卫峰, 刘三阳, 姜飞, 等. 混合人工蜂群算法[J]. 系统工程与电子技术, 2011, 33(5): 1167-1170. Gao W F, Liu S Y, Jiang F, et al. Hybird artificial bee colony algorithm[J]. Systems Engineering and Electronics, 2011, 33(5): 1167-1170.

[15]	Raquel C R, Jr Naval P C. An effective use of crowding distance in multiobjective particle swarm optimization[C]//Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation. New York, USA: ACM Press, 2005: 257-264.

[16]	邹文平. 人工蜜蜂群优化算法研究及应用[D]. 沈阳: 中国科学院沈阳自动化研究所, 2012. Zou W P. Research and application on artificial bee colony optimization algorithm[D]. Shenyang: Shenyang Institute of Automation, Chinese Academy of Sciences, 2012.

[17]	Liang J J, Qin A K, Suganthan P N, et al. Comprehensive learning particle swarm optinizer for global optimization of multimodal functions[J]. IEEE Transactions on Evolutionary Computation, 2006, 10(3): 281-295.

[18]	Li H, Zhang Q F. Multiobjective optimization problems with complicated pareto sets, MOEA/D and NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(2): 284-302.

[19]	Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.

[20]	Rahnamayan S, Tizhoosh H R, Salama M M A. Opposition-based differential evolution[J]. IEEE Transactions on Evolutionary Computation, 2008: 64-79.

"http://dx.doi.org/10.13976/j.cnki.xk.2015.0729"
中国科学院主管，中国科学院沈阳自动化研究所、中国自动化学会共同主办。

文章信息

宋晓宇, 张卿, 常春光

SONG Xiaoyu, ZHANG Qing, CHANG Chunguang

求解双层应急物资调度的改进蜂群算法

Improved Bee Colony Algorithm for Solving Double Layer Emergency Resource Scheduling

信息与控制, 2015, 44(6): 729-738.

INFORMATION AND CONTROL, 2015, 44(6): 729-738.

http://dx.doi.org/10.13976/j.cnki.xk.2015.0729

文章历史

收稿日期：2014-09-23

录用日期：2014-12-11

修回日期：2015-02-03

文章信息

文章历史

工作空间