2. 中国科学院上海高等研究院, 上海 201210
2. Shanghai Advanced Research Institute, Chinese Academy of Sciences, Shanghai 201210, China
1 引言
导航技术是自治移动机器人研究领域的核心技术,选择合适的传感器采集周围环境信息并通过有效的检测手段确定机器人自身位姿和周围环境状态是实现机器人导航的重要前提. 目前,雷达[1]、 声纳[2]和激光传感器[3]在导航领域均取得了成功应用. 视觉传感器作为一种新型导航方法依靠获取信息量大、 分辨率高和通用性强等优势[4],得到众多学者的青睐,如学者Hyukdoo[5]和Wang[6]等开展的视觉传感器研究. 值得注意的是他们采用的观测基准均为自然特征,提取路标的难度较大、 易受环境干扰而发生路标混淆现象,严重时将导致导航失败. 若在允许条件下,合理地设计和利用人工路标,能缓解路标特征化难度,形成稳定的数据关联,为导航算法提供更可靠的观测信息. 为此,一些研究者关注于特定环境下基于人工路标的视觉辨识. 其中,以Udo Frese为代表设计的人工路标[7],已得到了广泛应用[8, 9, 10, 11]. 本文在文[7]的研究背景下,采用空间转换和灰度值方差相结合的视觉特征辨识法,开展视觉导航定位的研究.
传感器观测噪声、 控制量生成噪声及对物理过程建模的偏差引起了移动机器人导航误差,研究者通常基于贝叶斯数据融合框架,通过反复的预测与更新过程优化系统后验概率的一致性[12, 13],例如,针对线性优化问题而提出的卡尔曼滤波(Kalman filter,KF). 而在真实环境中,机器人的运动模型和传感器的观测模型都是非线性的,为了融入贝叶斯数据融合框架,处理的方法之一是对非线性模型进行线性化处理(linearization),即,对非线性模型进行泰勒级数展开,然后采用忽略二次及多次项的方式强制使模型维持为线性[14]. 这种传统的处理方法,不可避免地会在线性化近似过程中引入误差,数据融合所经历的周期越多,这种误差累积越大. 为了改进传统算法——(extened Kalman filter,EKF)的缺陷,本文提出迭代观测更新策略,通过持续优化滤波更新的初始点,提升系统联合后验概率估计的精度,进而改进对机器人位姿与环境基元的估计质量.
2 视觉特征辨识本文所阐述的视觉特征辨识算法通过分析视觉传感器采集的图像信息,从背景2D图像中识别出人造特征点,并解算出特征点相对于机器人中心坐标系下的3D坐标[7],为后续数据融合算法提供环境观测基准.
2.1 辨识算法流程人工路标通常采用易于检测,与周围环境有明显区分的特征[15, 16]. 相比直线、 三角等其它图形,圆的表征简单且具有良好的对称性和旋转不变性,因此,本文选择圆盘标志作为人工路标. 如图 1所示为本文所使用的移动机器人平台所搭载的视觉传感器采集的1帧灰度图像,以及在机器人作业环境的地面上所布置的白色圆盘特征标志,其半径均设置为10 cm,它们即为待检测的目标特征.
 |
| 图 1 本文所设置的圆盘人造视觉特征Fig. 1 Circular artificial visual features |
以1帧图像为例说明圆形特征辨识过程,算法流程如图 2所示. 首先,依据设定的数据采集周期采集并读取1帧灰度图像; 然后,按照从左至右、 从上到下的顺序遍历图像中的像素点,并将满足如下条件的像素点坐标存储于表LUT1中,即,该像素点转换为3D坐标后,其Z方向坐标为0(即,该像素点位于地面); 与此同时,以该点为圆心,在水平面上构建半径分别为6 cm和14 cm的圆(预先根据像素分辨率和观察视角确定两圆的半径,以避免像素重合现象),并依次在两个圆周上进行均匀的N点采样,待该组采样点坐标映射到2D空间后,将其存储在表LUT2中. 依次类推,直到程序遍历完所有像素点为止. 再者,按顺序从表LUT2中取出每组采样点,根据其2D坐标得到相应灰度值,并利用其计算出大小圆的灰度值方差. 通过灰度值方差准则对圆心进行判断,如果该圆心对应的像素被判为目标圆的圆心像素点,则通过查询表LUT1,找出对应于该像素点的3D坐标并存储,此即为目标圆盘圆心在机器人坐标系中的坐标值. 重复上述检测步骤至遍历计算LUT2中的所有采样点.
 |
| 图 2 特征辨识算法流程Fig. 2 Flowchart of feature perception |
相机模型采用典型的针孔模型,并引入切向畸变和径向畸变. 空间映射将机器人中心坐标系下的3D坐标转换到图像中像素点的2D相平面坐标; 而空间逆映射实现相反的功能[17]. 在机器人坐标系中,将机器人的位姿记为[0,0,0]T,设相机中心的坐标为[cx,cy,cz]T,用z=0表示水平地面. 以[cx,cy,0]T作为坐标系原点,如图 3所示,O表示坐标原点,C和P分别表示相机中心和特征圆圆心所在位置,设P点坐标为[mx,my,mz]T. CP表示从相机中心发出并与地面相交的光射线,V点坐标记为[vx,vy,vz]T. CV和CP分别向平面ZOX投影得到CD和CA,其投影平面如图 3箭头所指的图形. 由几何比例关系可得到: mx=cx+vx·cz/vz,同理可得my=cy+vy·cz/vz. 由于特征圆全部粘贴于地面上,且在坐标系中与机器人位于同一个平面,其Z轴方向的坐标均为0,因此,用二维坐标[mx,my]T即可表示特征圆与机器人的相对位置关系.
 |
| 图 3 圆盘特征圆心坐标解算Fig. 3 Calculating of the centre coordinate of the disc features |
在以光射线交点为圆心所构建的大小圆的圆周上均匀采样N个点,利用空间映射算法将其转换到二维图像中. 通过灰度值方差准则,可以判别该交点是否为圆盘目标的圆心. 这里采用的灰度值方差法类似于Otsu提出的最大类间方差法[18],其方法描述如下:
在二维图像上,将小圆的N个采样点称为前景点,将大圆的N个采样点称为后景点,把前后景点分类并按顺序标记其灰度值为{g1,g2,…,gN}、 {gN+1,gN+2,…,g2N}. 记前景点和后景点出现的概率分别为w1和w2,记小圆和大圆的平均灰度值为μ1和μ2,两圆的总平均灰度值记为μ. 则两圆类间方差、 类内方差以及总方差计算如下:
(1) 大、 小圆平均灰度值和方差分别为




(2) 两圆的总平均灰度值:
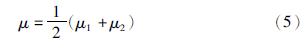
(3) 计算方差如下,分别称为类内方差和类间方差:
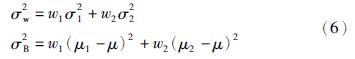
(4) 根据概率基本理论可知,总方差等于类间方差与类内方差之和,即:

在均匀材质及理想光照条件下,与目标圆盘圆心等距离处的像素灰度值变化相等. 排除两圆采样点均落在背景内导致类间方差与类内方差同为0的情况,并假设


在非理想条件下,可假设与目标圆同圆心的各圆圆周上像素灰度值方差最小,设σwmin2=p,可得:

因此,光射线交点与目标圆的圆心越接近,其类内方差越小,k值就越大,越接近η. 实际操作中,将η设为初始阈值,以仅能检测到一个圆心且误差较小为原则,通过反复实验修正阈值至效果最佳(实验中设定为0.6). 对于一个光射线交点,如果对应的2N个采样点灰度值经上述计算后,所得k值大于η,且大于其相邻像素为交点时所得的k值,则判定该像素点为目标圆圆心所在像素点. 其对应三维空间中的坐标值即为目标圆相对于机器人的位置.
3 迭代观测更新策略 3.1 概率理论移动机器人导航可等效为随机概率的状态估计问题,可将其描述为机器人基于环境观测信息,以一定的信度推理机器人和环境特征的联合后验概率[19, 20]. 假设每个时刻系统状态满足高斯分布,可用均值和方差唯一表示.
这里采用带有加性高斯噪声的状态空间方法表示迭代贝叶斯估计的运动模型和观测模型,分别表示如下:

根据条件概率知,当已知观测量{z1,z2,…,zj}时,可将系统的状态估计量和对应的方差[21]分别表示如下:

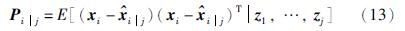
若当前时刻为t,根据式(12)对估计量的表示形式可得到:

 t|t表示在1∶t时刻所有观测量条件下得到的t时刻的状态估计量,
t|t表示在1∶t时刻所有观测量条件下得到的t时刻的状态估计量, t|t-1表示在1∶t-1时刻所有观测量条件下,对t时刻状态的预测估计量; xt表示t时刻的真实状态. 将预测的估计误差和方差分别表示如下:
t|t-1表示在1∶t-1时刻所有观测量条件下,对t时刻状态的预测估计量; xt表示t时刻的真实状态. 将预测的估计误差和方差分别表示如下:


当f(·)和h(·)为线性函数时,能形成闭合形式的迭代估计器. 但多数实际系统为非线性. 这违背了上述高斯分布闭合形式的假设. 通常采用的方法是通过线性化将系统模型强制近似为线性模型,再采用与线性模型相同的概率框架进行滤波估计,经典方法是将非线性系统模型在最佳似然估计值处进行泰勒级数展开,并忽略二次及多次项,即:


 f表示状态转移函数f(·)在xt=
f表示状态转移函数f(·)在xt= t-1|t-1处的雅可比矩阵,
t-1|t-1处的雅可比矩阵, h表示观测函数h(·)在预测状态向量xt=
h表示观测函数h(·)在预测状态向量xt= t|t-1处的雅可比矩阵.
t|t-1处的雅可比矩阵.
由于非线性的预测模型和观测模型均进行了线性化处理,由线性化而引起的误差会影响系统的估计精度. 为改进该缺陷,本文使用一次时间更新对应多次观测更新构成一次滤波周期的策略,该策略通过修正非线性观测函数的泰勒展开点的偏差,并对观测函数进行重复线性化来降低这种误差.
这里已知迭代的初始值为状态的预测估计量和方差,分别表示为 0=
0= t|t-1和P0=Pt|t-1(为简化表达式的表示方式,在本节中,省去了状态估计量和方差关于时间的下标. 例如将
t|t-1和P0=Pt|t-1(为简化表达式的表示方式,在本节中,省去了状态估计量和方差关于时间的下标. 例如将 t|t-1,i表示为
t|t-1,i表示为 i). 根据式(11),构造第i次状态更新中的伪观测量:
i). 根据式(11),构造第i次状态更新中的伪观测量:

根据式(19),可将伪观测量看作是关于xt的线性函数. 取式(19)在观测量{z1,z2,…,zt-1}下的条件均值:

定义伪新息如下:

由式(16)得到伪新息的方差为

将所求时刻的状态估计量定义为一步预测和伪观测量的线性加权和,即:

其中,K′i和Ki是表示加权矩阵.
将式(23)代入到式(15),得到状态估计量的误差:

由于E[vt]=0,E[ 0|z1,…,zt]=0和E[
0|z1,…,zt]=0和E[ i+1|z1,…,zt]=0,所以:
i+1|z1,…,zt]=0,所以:

 hi-I=0,所以:
hi-I=0,所以:

将式(26)代入式(23)和式(24)得到状态估计量的迭代表达式和误差表达式:


为使系统的状态估计误差最小,这里加权矩阵K′i的选择要使状态估计误差的方差最小. 因此首先计算估计误差的方差:
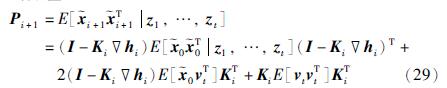


可将该式看作关于加权矩阵Ki的函数. 这里利用矩阵求导公式:

对式(31)求导并令导数为0,如下:
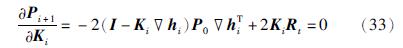
解上述等式,得出加权矩阵:

进而得到方差:

至此,得出了迭代观测更新策略的表达式,现根据式(27)、 式(34)、 式(35),总结如下:
将机器人的一步预测状态估计量作为初始状态的输入值:

状态的迭代观测更新过程如下:


这里,
式(36)、 式(37)和式(38)共同构成了迭代观测更新算法.
4 实验分析 4.1 实验设置实验引用了数据集DLR[7]. 该数据采集于德国宇航中心,通过搭载视觉传感器的移动机器人,观测并辨识29个房间中的人工圆盘路标图像信息,实验场地总面积为2 700 m2,机器人行驶轨迹全长505 m,实验过程中机器人路径包含3个闭合环路(loop). 利用第2节介绍的视觉特征辨识算法,可从图像信息中提取560个圆盘特征,并根据里程计信息解算出3 297组航位推算数据,每组数据包含世界坐标系下机器人的里程计数据和相对于机器人的人工路标观测信息. 机器人的运动模型和传感器的观测模型分别表示为式(39)和(40):


机器人在运动控制量的作用下,基于环境中的人工圆盘特征进行系统状态估计,实施闭环作业任务,出发点与终止点重合. 通过比较未加入迭代观测更新的传统算法和本文提出的加入迭代观测更新的算法,可验证迭代观测更新对系统后验概率估计质量的改善.
图 4所示为使用传统的贝叶斯滤波和本文所提出的加入了迭代观测更新的贝叶斯滤波算法所估计出的机器人轨迹对比,两种轨迹估计结果与整幢建筑的卫星影像相配准. 机器人运动的真实轨迹、 传统算法估计的机器人路径及本文所提出算法估计出的机器人路径分别在图上进行了标注. 由图可知,加入迭代观测更新后,机器人的定位路径更接近于真实路径,即,路径估计误差改善明显. 实验开展于本建筑的第1层,如图最左侧所示,机器人在控制量和运动模型的驱动下进行预测估计和运动,每4个运动间隔就对环境中的人工圆盘特征进行一次拍照观测,利用并提取人工路标信息后,对机器人的本次预测轨迹进行一次误差修正. 如此形成一个递归循环的过程,逐步完成由室内移动到室外的实时运动,具体可参见本实验的配套视频: http: //dwz.cn/iekfslam. 与室内环境相比,室外的地面平整度下降,机器人里程计数据的误差变大,因此,本文方法和传统方法的路径估计误差都明显增大. 当室外路径和室内路径共同形成了一个较大的闭合环路,即,机器人再次观测到先前的路标时,发生环路闭合(loop closure),系统的全局后验概率估计质量明显改善,因此,在图 4下部,接近起始点(即路径终止点)的部分,估计路径与真实路径间的误差显著降低.
 |
| 图 4 机器人的估计轨迹Fig. 4 Estimated trajectory of the robot |
图 5为机器人在移动过程中辨识并估计出的圆盘特征,它们构建出环境的轮廓地图,并将视觉特征的全局坐标配准到实验场地的建筑轮廓图上,比例尺及图例见图上标注. 由图可知,传统算法所辨识并估计出的视觉特征位置偏差较大. 而本文所提的加入迭代观测更新算法所估计的视觉特征点精度优于传统算法结果,能够与建筑物轮廓较好地配准.
 |
| 图 5 机器人作业过程中的视觉特征估计Fig. 5 The estimated visual features in the robot operations |
图 6中(a)、 (b)和(c)图比较了使用迭代观测更新前后机器人状态估计各维度上的绝对误差. 从3幅误差图中可知,随着时间的推移,传统的未加入迭代观测更新算法所产生的累积误差逐渐增大,而通过本文所提出的迭代观测更新的限定后,误差明显降低. 在t=2 500之后,机器人经历了由室内移动到室外又重回室内的环境变化过程,3个位姿方向上都出现了较大的误差,如前分析,这是由室外不平整的路面情况,使里程计观测混入较大的误差所致. 另外,在t =3 000时3个维度上的误差均突降,这体现出闭合环路对全局后验概率估计改善的效果.
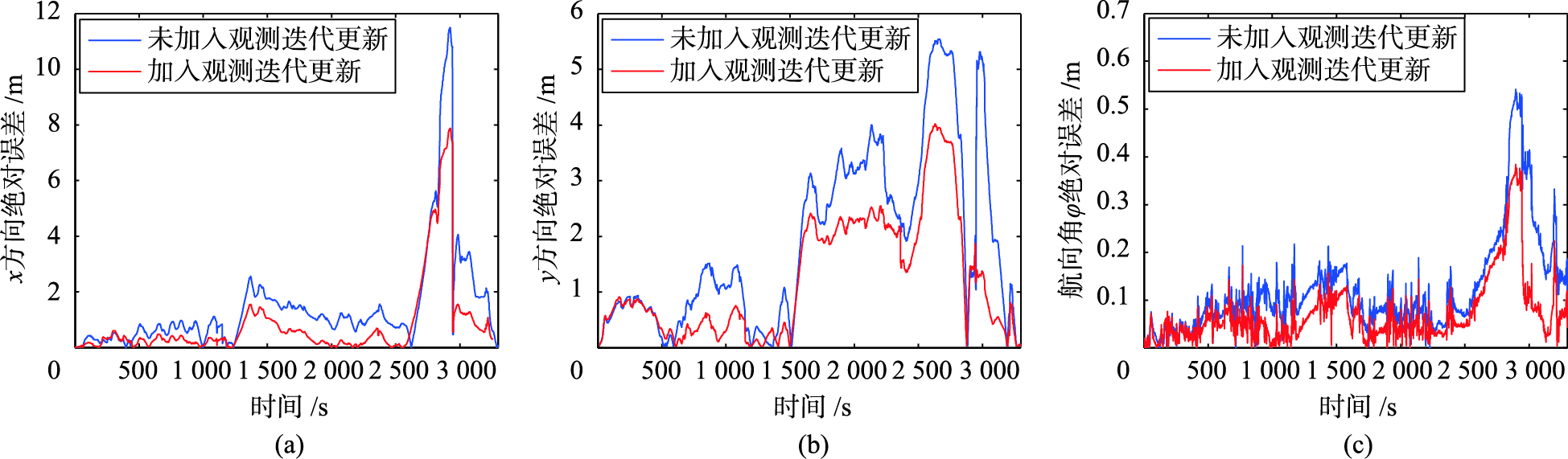 |
| 图 6 机器人状态估计的绝对误差Fig. 6 The absolute error of robot′s state estimation |
本文阐明了利用二维灰度图像解算圆形特征三维世界坐标的视觉特征辨识方法,并结合引入迭代观测更新的贝叶斯数据融合策略,提升移动机器人导航问题中全局后验概率估计的一致性. 通过实地实验,验证了本文所提算法在机器人自身位姿和视觉特征状态估计上优于传统算法的性能.
| [1] | Vivet D, Gérossier F, Checchin P, et al. Mobile ground-based radar sensor for localization and mapping: An evaluation of two approaches[J]. International Journal of Advanced Robotic Systems, 2013, 10(307): 12. |
| [2] | Fujimori A, Kubota H, Shibata N, et al. Leader-follower formation control with obstacle avoidance using sonar-equipped mobile robots[J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2014, 228(5): 303-315. |
| [3] | Sarkar B, Pal P K, Sarkar D. Building maps of indoor environments by merging line segments extracted from registered laser range scans[J]. Robotics and Autonomous Systems, 2014, 62(4): 603-615. |
| [4] | Dawadee A, Chahl J, Nandagopal D, et al. Illumination, scale and rotation invariant algorithm for vision-based UAV navigation[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2013, 27(5): DOI: 10.1142/S0218001413590039. |
| [5] | Choi H, Kim R, Kim E. An efficient ceiling-view SLAM using relational constraints between landmarks[J]. International Journal of Advanced Robotic Systems, 2014, 11(1): 4. |
| [6] | Wang Y T, Lin G Y. Improvement of speeded-up robust features for robot visual simultaneous localization and mapping[J]. Robotica, 2014, 32(4): 533-549. |
| [7] | Kurlbaum J, Frese U. A benchmark data set for data association[J]. Bremen, Germany: University of Bremen, 2009. |
| [8] | Song Y, Li Q, Kang Y. Conjugate unscented fast SLAM for autonomous mobile robots in large-scale environments[J]. Cognitive Computation, 2014, 6(3): 496-509. |
| [9] | Zhao L, Huang S, Dissanayake G. Linear SLAM: A linear solution to the feature-based and pose graph SLAM based on submap joining [C]//Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Piscataway, NJ, USA: IEEE, 2013: 24-30. |
| [10] | Ceriani S. Conditionally independent visual slam with integrated bundle adjustment[M]//Washington, USA: National Geographic Society, 2013. |
| [11] | Qayyum U, Kim J. Global optimization for 2D SLAM problem[M]//Informatics in Control, Automation and Robotics. Berlin, Germany: Springer, 2014: 35-49. |
| [12] | Huang D, Cai Z, Wang Y, et al. A real-time fast incremental SLAM method for indoor navigation[C]//Proceedings of the Chinese Automation Congress (CAC). Piscataway, NJ, USA: IEEE, 2013: 171-176. |
| [13] | de la Puente P, Rodriguez-Losada D. Feature based graph-SLAM in structured environments[J]. Autonomous Robots, 2014, 37(3): 243-260. |
| [14] | Shojaei K, Shahri A M. Experimental study of iterated Kalman filters for simultaneous localization and mapping of autonomous mobile robots[J]. Journal of Intelligent & Robotic Systems, 2011, 63(3/4): 575-594. |
| [15] | Rao T V, Rao M V V, Narasaiah P. Mobile robot self-planning and navigation based on artificial landmark localization method and binocular stereo vision[C]//Proceedings of the International Journal of Engineering Research and Technology. Tallahassee, FL, USA: ESRSA Publications, 2012. |
| [16] | Pinto M, Santos F, Moreira A P, et al. Robust and fast algorithm for artificial landmark detection in an industrial environment[J]. Journal of Automation and Control Engineering, 2013, 1(2): 125-138. |
| [17] | Nieto M, Laborda J A, Salgado L. Road environment modeling using robust perspective analysis and recursive Bayesian segmentation[J]. Machine Vision and Applications, 2011, 22(6): 927-945. |
| [18] | Otsu N. A threshold selection method from gray-level histograms[J]. Automatica, 1975, 11(285/286): 23-27. |
| [19] | Bergman N. Recursive Bayesian estiatiomn[D]. Linköping, Sweden: Linköping University, 1999, 579. |
| [20] | Thrun S, Burgard W, Fox D. Probabilistic robotics[M]. Cambridge, MA, USA: MIT Press, 2005. |
| [21] | Durrant-Whyte H F. Introduction to estimation and the Kalman filter[D]. Sydney, Australian: The University of Sydney, 2001. |



