2. 武汉理工大学交通学院, 湖北 武汉 430063
2. School of Transportation, Wuhan Uninversity of Technology, Wuhan 430063, China
1 引言
随着城市化和交通机动化进程加快,城市道路交通网络不断扩大,交通拥堵逐渐加剧,交通运行效率逐步降低,给城市交通管理带来了巨大压力. 交叉口是城市路网通行能力的瓶颈点,交叉口管控水平直接影响到路网的通行效率. 交通延误作为路网运行效率的主要衡量指标,在非拥堵路网中,交通延误主要发生在交叉口. 而交通信号控制是交叉口延误的主要来源,因此,有必要对交叉口信号控制进行优化,以提高路网运行效率. 目前,虽然有部分城市在一定范围内采用了交叉口区域协调控制,但是绝大部分的城市信号交叉口仍然采用多时段定相位或定周期的感应控制方式. 定周期或定相位的感应控制不能动态变化控制参数以适应随机波动较大的交通流,从而导致部分相位流线的绿灯损失和增加交叉口的控制延误. 随着大数据时代的到来和交通数据采集技术的发展和运用,利用采集到交叉口的实时数据,结合流线消散模型和逻辑规则,可实现交叉口按照进口各流线实时消散进行动态逻辑组合控制.
交叉口信号控制优化一直是交通控制领域的研究热点,并随着技术的革新和理论的发展在不断地进步. 早期的交叉口控制优化研究主要致力于在定周期条件下进行单目标或多目标优化[1, 2, 3],然后采用不同的方法优化动态配时[4, 5, 6],接着研究在固定相位条件下多相位及变相序控制优化模型及算法[7, 8, 9, 10]. 近年来逐步采用系统理论和方法研究交叉口的控制问题. 高海军等[11]采用集合理论对交通路口可变相位信号控制进行阐述; 赵忠杰等[12]利用模糊控制理论,提出单交通路口变相位变周期信号控制; 陈智等[13, 14]利用模糊控制理论抑制过饱和交叉口交通信号; 陈娟等[15, 16, 17]对交叉口进行自适应控制研究. 目前的研究成果奠定了交叉口复杂控制的理论基础,然而对交叉口的交通流线按照实时消散的动态逻辑组合控制的研究成果仍然较少,且未考虑更全面的相位流线组合,以及提出具体的流线动态逻辑组合控制过程.
交叉口进口转向流线的车辆到达具有随机动态特性,通过交叉口各转向流线动态组合,建立消散模型和控制模型,得到的控制方案与交通流线到达的随机性将更加协调. 从而降低交叉口的延误,提升交叉口的时空利用效率和交叉口控制智能化水平.
2 可行控制相位集合交叉口控制相位的流线组合由各转向交通流线的交通特性决定,为保证流线行驶安全,同一相位中各交通流线应具有相容关系. 所谓交通流线相容关系指各交通流在无冲突条件下能够同时获得通行权的一系列流线搭配.
以典型的十字交叉口为例,每一进口道三车道按交通流向进行车道分离,具体交叉口布局形式及检测线圈位置布置如图 1所示.
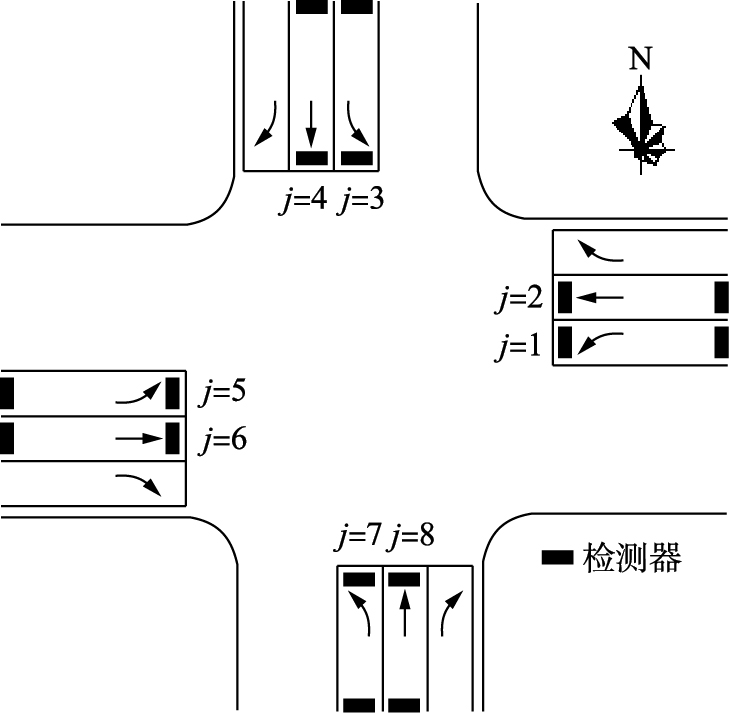 |
| 图 1 典型交叉口Fig. 1 Typical intersection |
交通流线采用σi,jl表示,其中l表示周期; i为相位序号,相位集合为{i|i=1,2,3,4}; j为交通流线,流线集合为{j|j=1,2,3,4,5,6,7,8},分别表示交叉口入口东左、 东直、 北左、 北直、 西左、 西直、 南左、 南直交通流线方向. 若某流线有多个进口车道,则该流线的车辆到达率、 消散时间和通行能力等与车道数量相关的指标按照车道组的概念进行换算.
当典型交叉口出口车道数与相容流线需要的出口车道数相匹配时,合流流线之间没有合流交织的安全隐患; 当交叉口出口车道数小于相容流线的出口车道数量需求时,理论上可能出现两股交通流的合流冲突,但根据交通规则,转向应让直行. 因此,动态流线逻辑组合的安全隐患较小,如果都按照交通规则运行,理论上是没有影响的,故可将合流流线作为相容流线考虑. 依据交叉口各交通流线之间的相容性,按两两组合可分为12组,记为Am(m=1,2,…,12),如表 1所示.
| 相容组合Am | 交通流线序号 | 相容组合Am | 交通流线序号 | |
| A1 | σi,1l σi,5l | A7 | σi,5l σi,6l | |
| A2 | σi,2l σi,6l | A8 | σi,7l σi,8l | |
| A3 | σi,3l σi,7l | A9 | σi,1l σi,4l | |
| A4 | σi,4l σi,8l | A10 | σi,3l σi,6l | |
| A5 | σi,1l σi,2l | A11 | σi,5l σi,8l | |
| A6 | σi,3l σi,4l | A12 | σi,2l σi,7l |
由表 1可知,每一流线都存在3个流线与其相容,常用十字交叉口四相位定相控制方案就是采用表 1中的4组数据进行控制. 在定相位控制条件下,相位组合中两流线的车辆到达波动大或两流线需要的消散时长差值较大时,容易产生某一流线的绿灯损失,故不能完全利用交叉口的通行能力. 因此,有必要根据车流到达情况对交叉口的相位流线组合进行动态调整,优化控制相位的流线组合方案,实现交叉口的动态控制.
根据交通流相容性以及周期内每一流线放行一次的原则,采用逻辑数学将相容组合Am作为逻辑输入变量,逻辑函数为
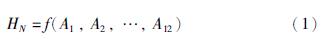
变量Am的取值为0或1,取值为0表示当前周期不采用对应交通流流向组合形式; 取值为1表示当前周期某一相位采用该组合形式. 当变量取值确定后,逻辑函数HN(N表示HN的取值个数)取值0或1由A1,A2,…,A12和逻辑函数f共同决定,逻辑函数f表示变量Am中有4个变量取值为1且该4个变量是否包含交叉口8股流线,若包含则HN=1; 若不包含则HN=0.
通过逻辑函数进行计算后,令Fn={(σi,υl σi,θl)HN=1的条件下,取Am=1所对应的流线组合},υ,θ∈{j|j=1,2,3,4,5,6,7,8},n表示HN=1的个数.
如果A1=A2=A3=A4=1,A5=A6=A7=A8=A9=A10=A11=A12=0,HN=1,则有F1={(σi,1l σi,5l),(σi,2l σi,6l),(σi,3l σi,7l),(σi,4l σi,8l)}.
3 实时消散模型研究 3.1 流线实时消散计算模型一般情况下,车辆到达率是随时间变化的,记周期l流线j的到达率为Qjl(t),实时消散过程如图 2所示[18, 19].
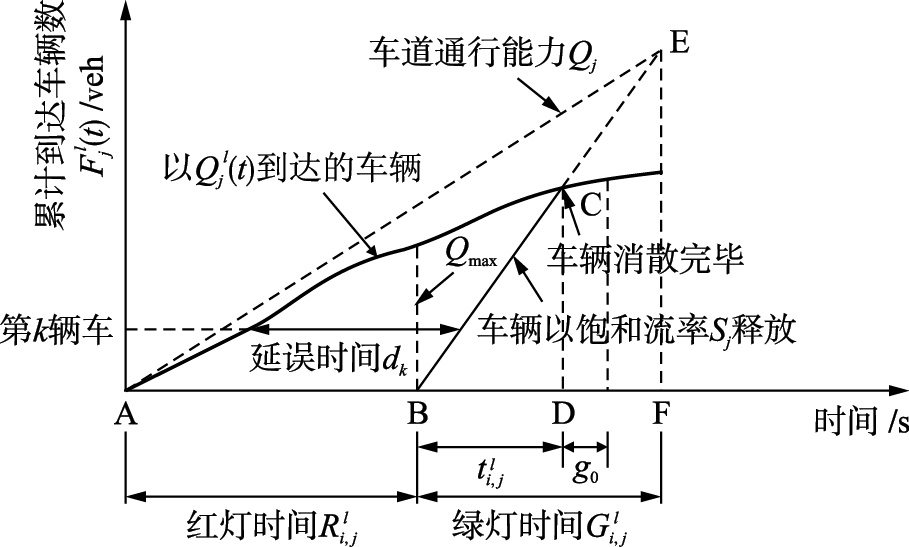 |
| 图 2 实时消散过程图Fig. 2 The process diagram of real-time dissipation |
图 2中,A点对应红灯起始时刻,B点对应绿灯起始时刻,F点对应绿灯结束时刻. AC为车辆到达曲线,BC的斜率为进口道饱和流率,交点C对应排队消失时刻D. 斜线BC的延长线与过F点的垂线相交于E,线段FE表示绿灯时间流线j最多能够放行的车辆数,斜线AE的斜率表示进口流线j的通行能力.
流线j的消散时刻累积到达车辆数为
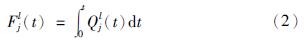
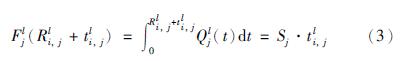
为了简化计算,假设流线j的车辆到达率在一个周期内保持不变,即Qjl(t)=Qlj,可通过排队车辆数与等待时间确定,则有

通过此消散模型,可计算各流线消散时间,进而对流线延误进行分析.
3.2 延误评价指标计算图 2中,信号周期l内,车道j全部通过车辆的总延误时间Djl即车辆延误时间dkl的总和,等于曲边三角形ABC的面积. 即:
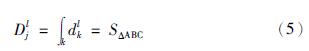
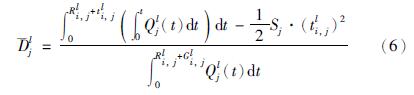
车辆在一个信号周期与另一个信号周期之间是有随机波动的,Webster提出随机波动对交叉口车辆所产生的延误称为随机平均延误,各流线随机平均延误计算公式为[20]
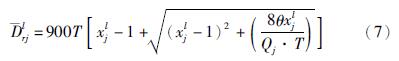
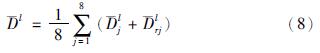
城市交叉口控制过程以消散时间最长流线作为优先选择的控制流线,以此降低交叉口车辆的平均延误. 因此,将消散时间最长流线与消散时间相近且不冲突的流线进行动态逻辑组合,生成相位实现交叉口的动态控制.
4.1 流线实时逻辑值的确定在实时消散模型求解流线消散时间过程中,必须求出流线计算时刻等待的红灯时间,为此在控制过程中流线用符号σ=(i,l, j)表示,并将流线实时消散时间作为逻辑值. 具体求解过程如图 3所示.
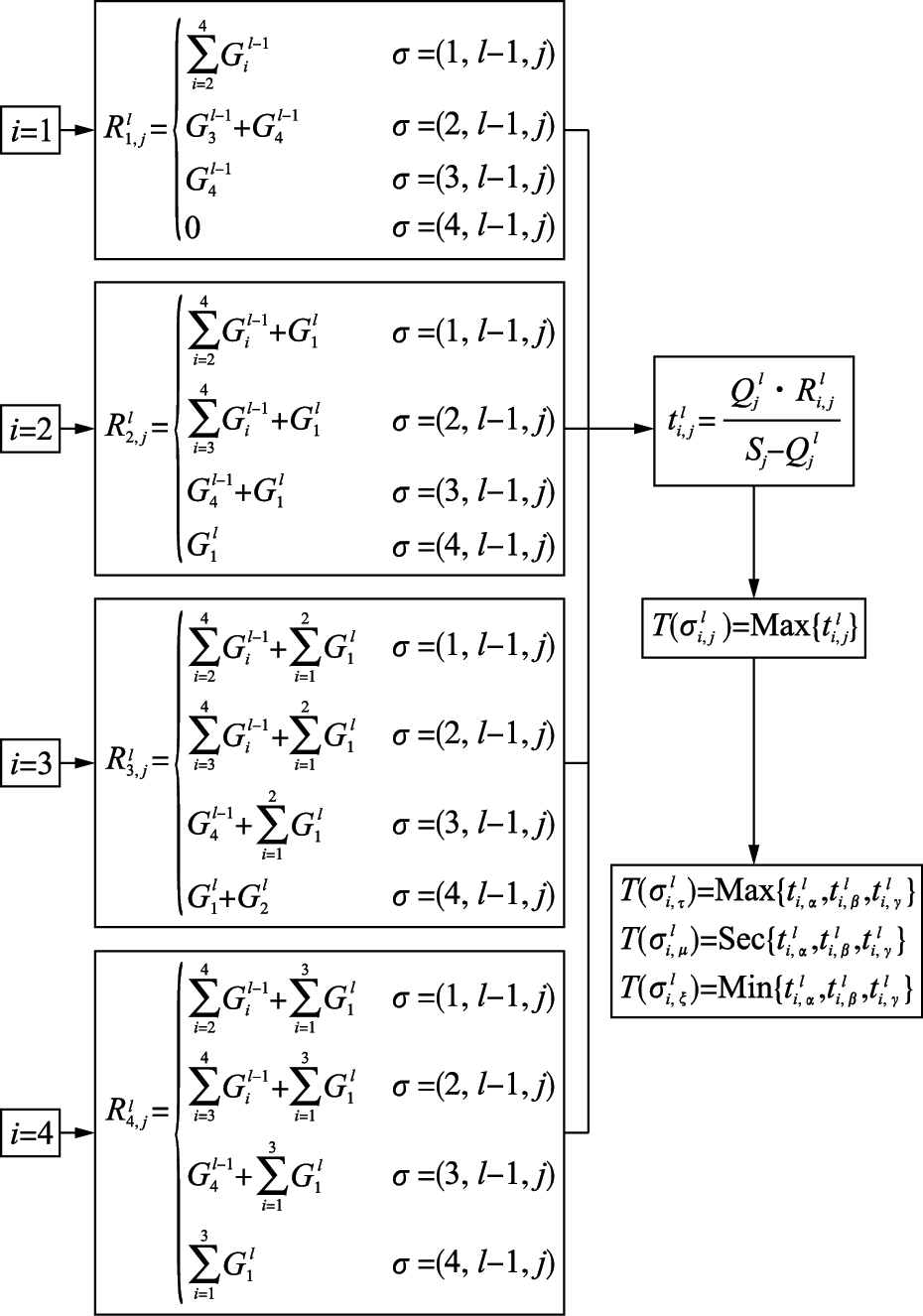 |
| 图 3 交通流线逻辑值计算流程图Fig. 3 The process diagram of calculating traffic streamline logical values |
图 3中,σ=(i,l-1,j)表示计算时刻流线j在第l-1周期作为第i相位放行; α,β,γ,τ,μ,ξ∈{j|j=1,2,…,8}且{τ,μ,ξ}={α,β,γ}; 流线σi,αl,σi,βl,σi,γl表示流线σi,jl的3条相容流线; 函数T(σi,μl)=Sec{ti,αl ,ti,βl ,ti,γl }表示流线σi,αl,σi,βl, σi,γl第二位消散时间所对应的流线σi,μl(μ=α或β或γ).
如第l周期第2相位时刻,计算流线σ=(2,l-1,j)的逻辑值. 流线σ等待的时间为R2,jl =G3l-1 +G4l-1 +G1l ,如图 4所示.
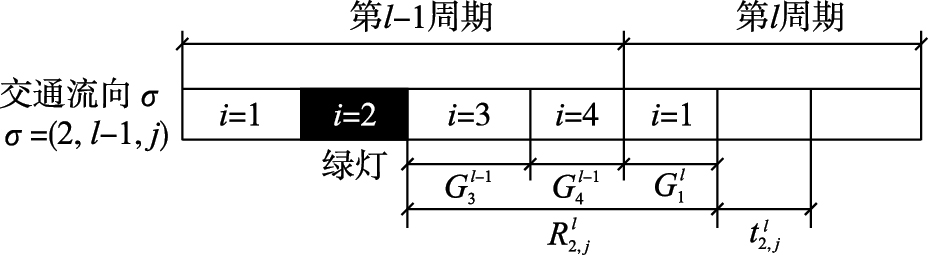 |
| 图 4 交通流线等待时间图Fig. 4 Latency time diagram of traffic streamline |
由图 5可知,消散时间计算模型为
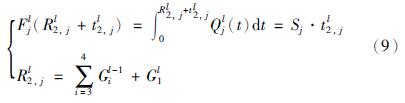
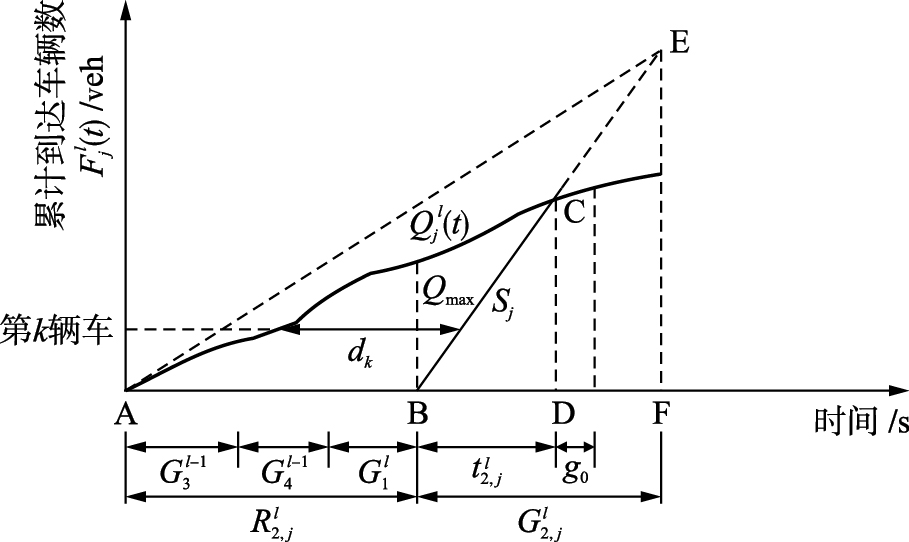 |
| 图 5 交通流线消散时间计算图Fig. 5 Dissipation time calculation diagram of traffic streamline |
为了简化计算,采用周期平均到达率Qjl(t)=Qjl ,则有
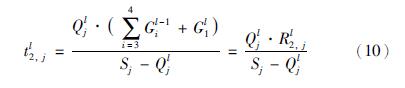
由此可以确定流线任意时刻的逻辑值,为后续流线动态逻辑组合以及配时做好铺垫. 本文目前仅考虑消散时间大小作为流线优先组合逻辑值,后续研究除考虑流线消散时间外,将增加优先选择指标作为流线逻辑值,如: 流线车辆组成、 相临车道之间车辆的影响和道路等级等指标综合考虑,使流线优先选择更加符合实际情况.
4.2 相位流线动态逻辑组合通过流线逻辑值计算流程图,能够得到相位初始计算时刻各流线的逻辑值,则将周期前3相位初始时刻中最大的逻辑值流线依次记为σ1,jl,σ2,jl,σ3,jl; 再根据逻辑值即消散时间相近且流线相容的组合原则确定相位流线组合; 最后将剩余未放行的两流线作为第4相位放行,从而实现实时动态逻辑控制. 具体实时动态逻辑组合过程如图 6所示.
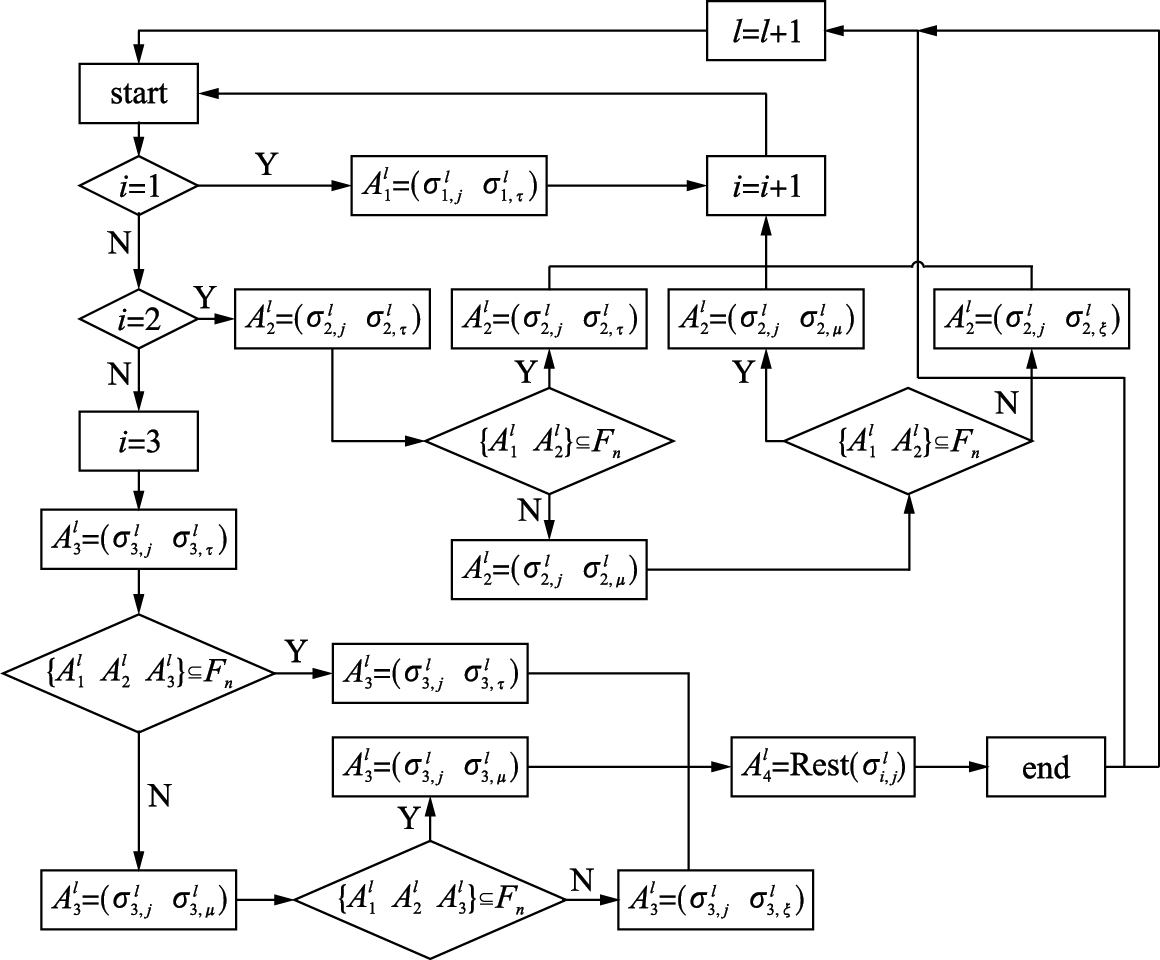 |
| 图 6 流线动态逻辑组合图Fig. 6 Dynamic logical combination diagram of the streamline |
图 6中,A1l ,A2l ,A3l , A4l 代表l周期的4个相位组合; A4l =Rest(σi,jl)代表剩下未放行流线组合为相位4.
在确定周期控制相位组合后,将计算得到的流线消散时间与Gmin和Gmax相比较以确定感应配时的起步绿灯时长. Gmax是以交通心理学中驾驶员能够忍受的最长等待时间为基础考虑,因此驾驶员所等待的时间处于可接受范围以内,目的在于考虑等待通行驾驶员的舒适性和安全性. 在信号控制中,将相位中2流线消散时间较大的作为绿灯显示时间,采用流线较短绿灯延长时间作为相位绿灯延长时间,目的在于尽量减少相位绿灯的损失时间. 则l周期各相位实际绿灯时间为Gil =max{ti,jl }+w·g0,但Gmin≤Gil ≤Gmax(w为非零正整数,g0为单位绿灯延长时间,Gmin为相位最小绿灯时间,Gmax为最大绿灯延长时间). 当延长一个单位绿灯时间后无后续来车,则实际绿灯时间Gil =max{ti,jl }+g0,若max{ti,jl }+g0<Gmin,则相位绿灯时间为Gil =Gmin; 若max{ti,jl }+w·g0>Gmax,则Gil =Gmax.
绿灯延长时间采用黄闪的形式进行控制,当流线没有后续来车或者到达最大绿灯时间时,为了保证车辆行驶的安全性,设置一定的黄灯时间,一般为3 s. 通过上述流线动态逻辑组合控制过程,可得到各周期信号控制方案,从而实现交叉口的实时动态控制.
5 实例分析重庆南岸区某十字交叉口有环形人行天桥,现状采用定相位感应控制方式,其渠化后的现状交叉口形式如图 7所示; 调查采集到的各时段流线平均到达率如表 2所示.
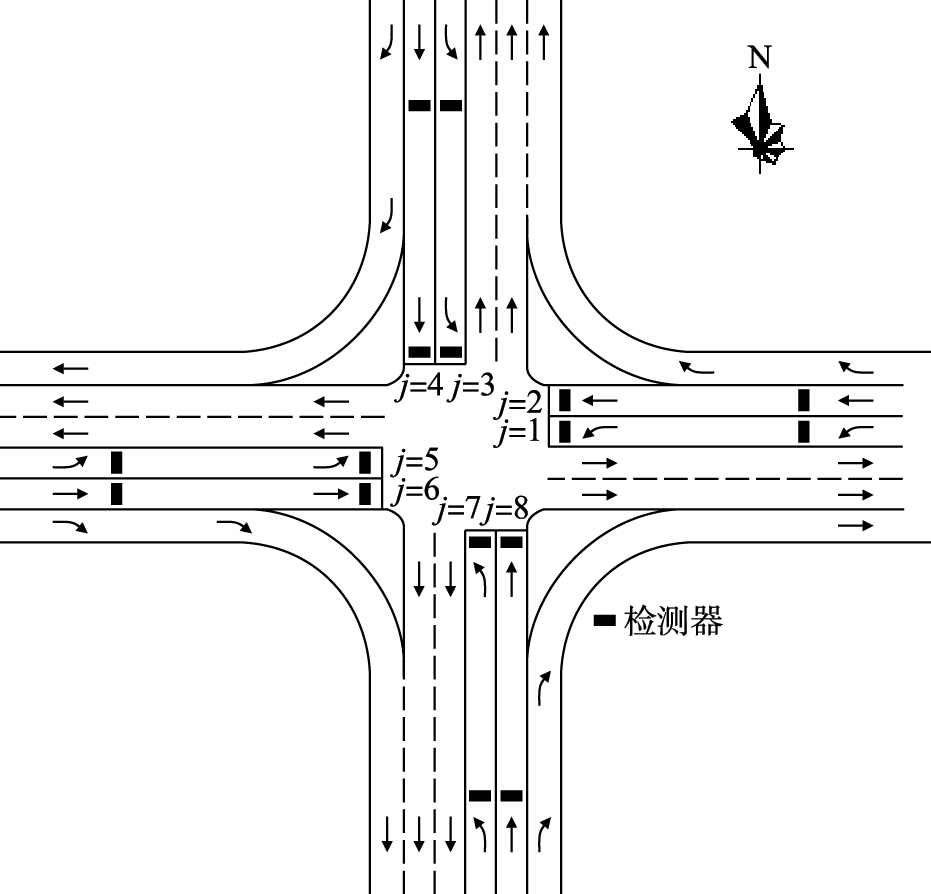 |
| 图 7 现状交叉口形式Fig. 7 The shape of existing intersection |
| 时段 | 交通流向j/(pcu/s) | |||||||
| j=1 | j=2 | j=3 | j=4 | j=5 | j=6 | j=7 | j=8 | |
| 1 | 0.184 | 0.158 | 0.159 | 0.149 | 0.098 | 0.140 | 0.135 | 0.148 |
| 2 | 0.073 | 0.107 | 0.048 | 0.105 | 0.071 | 0.103 | 0.120 | 0.068 |
| 3 | 0.088 | 0.068 | 0.073 | 0.069 | 0.056 | 0.111 | 0.121 | 0.138 |
| 4 | 0.054 | 0.052 | 0.086 | 0.100 | 0.063 | 0.070 | 0.053 | 0.091 |
| 5 | 0.112 | 0.077 | 0.157 | 0.131 | 0.106 | 0.113 | 0.106 | 0.132 |
| 6 | 0.071 | 0.113 | 0.088 | 0.123 | 0.104 | 0.122 | 0.043 | 0.125 |
| 7 | 0.050 | 0.057 | 0.105 | 0.080 | 0.073 | 0.110 | 0.069 | 0.062 |
| 8 | 0.131 | 0.144 | 0.106 | 0.184 | 0.161 | 0.118 | 0.153 | 0.165 |
| 9 | 0.104 | 0.119 | 0.128 | 0.035 | 0.073 | 0.088 | 0.137 | 0.036 |
| 10 | 0.167 | 0.090 | 0.103 | 0.114 | 0.108 | 0.058 | 0.099 | 0.103 |
| 11 | 0.057 | 0.135 | 0.099 | 0.180 | 0.110 | 0.111 | 0.083 | 0.104 |
| 12 | 0.107 | 0.053 | 0.037 | 0.041 | 0.096 | 0.101 | 0.054 | 0.048 |
| 13 | 0.070 | 0.104 | 0.105 | 0.078 | 0.123 | 0.098 | 0.119 | 0.079 |
| 14 | 0.089 | 0.087 | 0.054 | 0.091 | 0.064 | 0.075 | 0.116 | 0.122 |
| 15 | 0.119 | 0.124 | 0.127 | 0.081 | 0.116 | 0.104 | 0.121 | 0.118 |
| 16 | 0.137 | 0.095 | 0.153 | 0.112 | 0.075 | 0.092 | 0.105 | 0.099 |
| 17 | 0.074 | 0.129 | 0.104 | 0.115 | 0.088 | 0.104 | 0.137 | 0.127 |
| 18 | 0.030 | 0.056 | 0.072 | 0.144 | 0.054 | 0.141 | 0.058 | 0.107 |
| 19 | 0.121 | 0.107 | 0.074 | 0.039 | 0.130 | 0.091 | 0.116 | 0.088 |
| 20 | 0.132 | 0.115 | 0.106 | 0.108 | 0.107 | 0.042 | 0.119 | 0.134 |
该交叉口现阶段受上下游控制和交通干扰导致流线的到达率具有较大波动性,经常由于现有控制方式导致流线的绿灯损失,从而加剧交通拥堵. 运用均衡消散模型对其进行实时动态控制计算,交叉口直行流线饱和流率为1 650辆/h,左转流线的饱和流率为直行的95%; 相位的最小绿灯时间Gmin取10 s; 相位的最大绿灯时间Gmax为60 s; 对20个周期的车辆到达率进行计算,得到各周期流线组合、 相位配时以及周期平均延误,如表 3所示.
| 周期 | 最佳流线组合 | 相位配时/s | 周期时长/s | Dl/s | ||||||
| A1l | A2l | A3l | A4l | G1l | G2l | G3l | G4l | |||
| 1 | A5 | A6 | A8 | A7 | 21 | 17 | 29 | 21 | 88 | 13 |
| 2 | A5 | A6 | A8 | A7 | 31 | 26 | 33 | 27 | 117 | 28 |
| 3 | A5 | A8 | A6 | A7 | 30 | 23 | 27 | 27 | 107 | 35 |
| 4 | A8 | A5 | A6 | A7 | 21 | 26 | 19 | 12 | 79 | 32 |
| 5 | A8 | A6 | A5 | A7 | 17 | 14 | 17 | 17 | 66 | 19 |
| 6 | A4 | A3 | A2 | A1 | 20 | 22 | 18 | 20 | 81 | 30 |
| 7 | A4 | A10 | A12 | A1 | 21 | 18 | 12 | 11 | 62 | 25 |
| 8 | A4 | A10 | A12 | A1 | 13 | 13 | 17 | 27 | 70 | 24 |
| 9 | A4 | A3 | A2 | A1 | 26 | 28 | 32 | 28 | 114 | 34 |
| 10 | A3 | A5 | A4 | A7 | 26 | 26 | 25 | 24 | 101 | 35 |
| 11 | A5 | A6 | A8 | A7 | 23 | 26 | 32 | 29 | 110 | 36 |
| 12 | A5 | A6 | A7 | A8 | 30 | 31 | 18 | 18 | 98 | 43 |
| 13 | A5 | A7 | A3 | A4 | 21 | 15 | 16 | 15 | 67 | 29 |
| 14 | A5 | A7 | A8 | A6 | 14 | 14 | 17 | 11 | 55 | 27 |
| 15 | A5 | A7 | A8 | A6 | 12 | 11 | 14 | 16 | 53 | 28 |
| 16 | A5 | A7 | A3 | A4 | 17 | 17 | 18 | 20 | 72 | 26 |
| 17 | A5 | A3 | A7 | A4 | 21 | 21 | 22 | 24 | 88 | 31 |
| 18 | A12 | A10 | A9 | A11 | 21 | 19 | 19 | 19 | 79 | 38 |
| 19 | A2 | A3 | A1 | A4 | 16 | 17 | 15 | 12 | 59 | 26 |
| 20 | A12 | A10 | A1 | A4 | 14 | 14 | 17 | 19 | 65 | 23 |
交叉口现状控制方案采用的是固定相位感应配时,现状所采用的固定相位为传统的4相位控制A5、 A6、 A7、 A8,即每一进口作为一相位放行. 对于现状固定相位感应配时控制延误的计算采用的是Webster提出的计算延误的一般公式,固未在论文中详细罗列. 由于实时动态控制数据采用延误计算公式,故可求得均衡延误和随机平均延误如表 4及图 8所示. 并采用Synchro 7.0软件分别对现状感应控制相位和实时动态控制所对应的相位控制进行仿真分析,提取仿真结果中的延误示意图. 图 9和图 10中不同颜色代表着进口流线的不同车辆平均延误.
| 控制方式 | 均衡延误/(s/pcu) | 随机平均延误/(s/pcu) | 总平均延误/(s/pcu) |
| 现状感应控制 | 33.56 | 17.51 | 51.07 |
| 动态逻辑控制 | 19.67 | 10.69 | 30.36 |
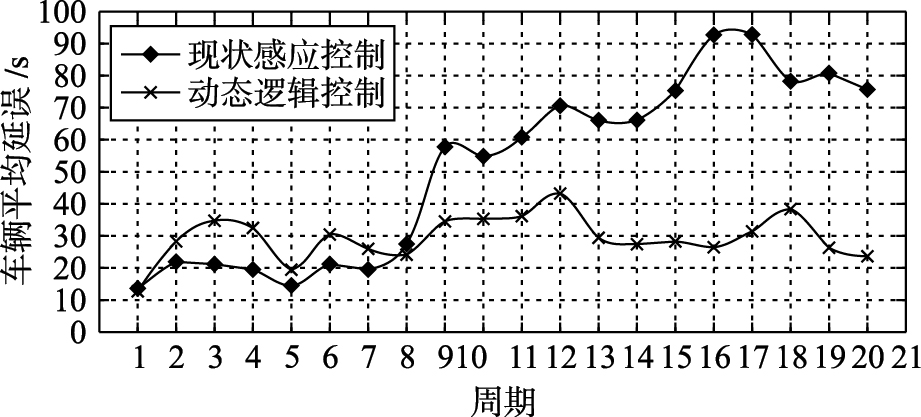 |
| 图 8 各周期延误对比图Fig. 8 The contrast figure of each cycle delay |
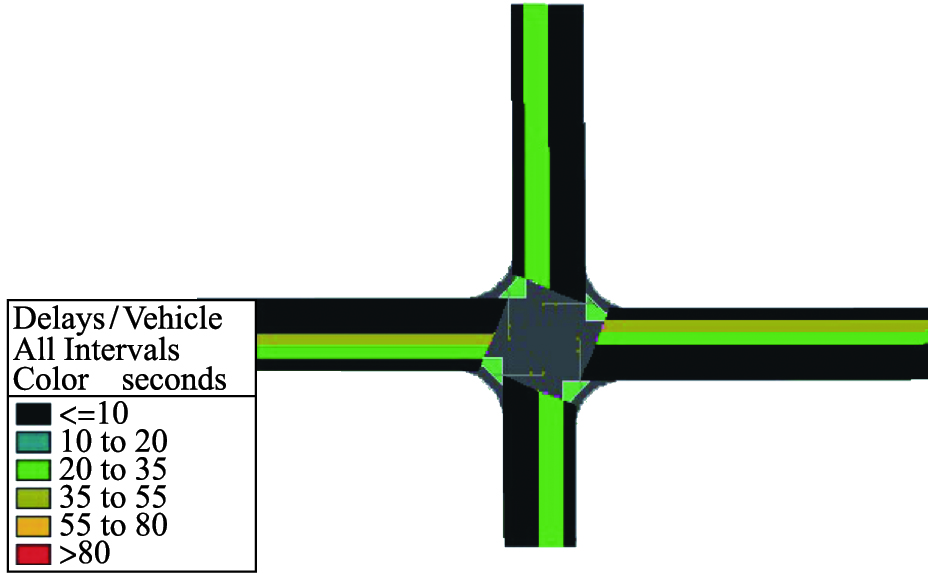 |
| 图 9 定相位感应控制Fig. 9 The sensing signal control of fixed phases |
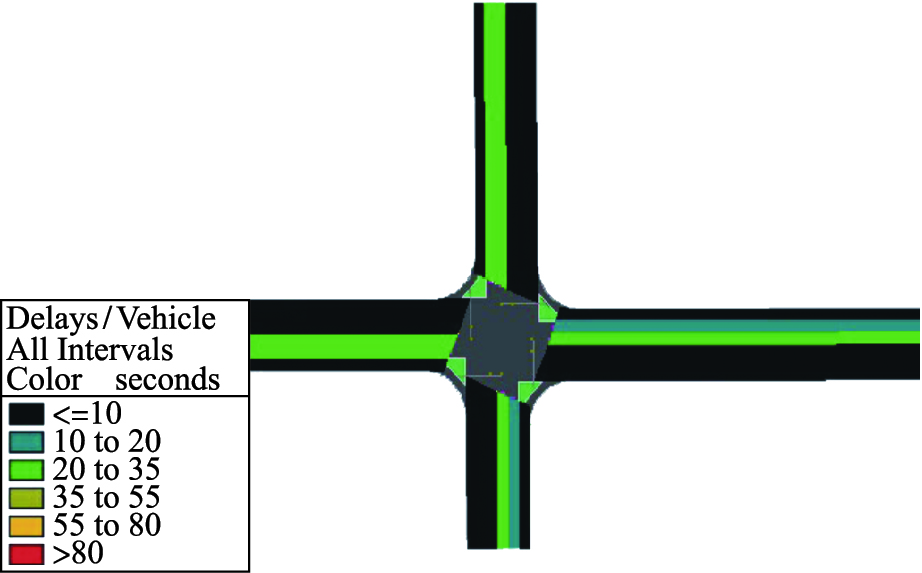 |
| 图 10 动态逻辑组合控制Fig. 10 Dynamic logical combination control |
由表 4可知,定相位控制方案中车辆平均延误为51.07 s/pcu,流线实时动态控制优化方案车辆平均延误为30.36 s/pcu,故车辆总平均延误明显降低; 图 8表明实时动态控制不仅能够减少延误也可以预防交通拥堵. 由图 9可知,感应控制下东西直行流线呈黄色,说明平均延误相对较大. 图 10表明对于同一流线到达实时动态控制下的各流线都为绿色,说明平均延误小,控制效果较好. 产生这样差异的原因在于两种控制方案的控制相位不同,在交叉口流线到达波动较大情况下,控制相位的选择直接影响交叉口的控制效果.
综上可知,实时消散的动态逻辑组合控制与交通流的随机变化协调性更好,能够显著地减少车辆行程延误,缓解交通拥堵.
6 结论以减少延误为出发点,利用交叉口采集到的交通流线的实时数据,建立部分交通流线未饱和状态下的信号交叉口均衡消散模型,以消散时间作为逻辑值,提出交叉口流线动态逻辑组合的优化控制方法. 通过实例验证流线实时消散的动态逻辑组合控制的优越性. 相比多时段定相位或定周期的感应控制,流线动态逻辑组合控制方式与交叉口各转向流量结合紧密,降低了交叉口车辆的平均延误,提升了交叉口信号控制智能化水平以及交叉口的通行能力.
| [1] | 高云峰, 徐立鸿, 胡华, 等. 交叉口定周期信号控制多目标优化方法[J]. 中国公路学报, 2011, 24(5): 82-87. Gao Y F, Xu L H, Hu H, et al. Multi-objective optimization method for fixed-time signal control at intersection[J]. China Journal of Highway and Transport, 2011, 24(5): 82-87. |
| [2] | 马莹莹, 杨晓光, 曾滢. 信号控制交叉口周期时长多目标优化模型及求解[J]. 同济大学学报: 自然科学版, 2009, 37(6): 761-765. Ma Y Y, Yang X G, Zeng Y. Multi-objective cycle length optimization model and solution[J]. Journal of Tongji University Natural: Science Edition, 2009, 37(6): 761-765. |
| [3] | Dion F, Rakha H, Kang Y S. Comparison of delay estimates at under-saturated and over-saturated pre-timed signalized intersections[J]. Transportation Research, Part B: Methodological, 2004, 38(2): 99-122. |
| [4] | 梁骁, 殷勇辉, 吴颜. 单交叉口信号配时的动态优化[J]. 公路交通技术, 2010, 2(4): 125-127. Liang X, Yin Y H, Wu Y. Dynamic optimization for signal timing a single crossings[J]. Technology of Highway and Transport, 2010, 2(4): 125-127. |
| [5] | 李明利, 赵祥模, 张利川, 等. 基于排队状态的单点交叉口动态信号配时算法[J]. 交通运输工程学报, 2008, 8(5): 100-103. Li M L, Zhao X M, Zhang L C, et al. Dynamic signal timing algorithm at single-point intersection based on queuing condition[J]. Journal of Traffic and Transportation Engineering, 2008, 8(5): 100-103. |
| [6] | 首艳芳, 徐建闽. 信号交叉口多目标动态决策模型及其优化方法[J]. 公路交通科技, 2012, 29(11): 92-97. Shou Y F, Xu J M. Multi-objective dynamic decision-making model of signalized intersection and its optimization method[J]. Journal of Highway and Transportation Research and Development, 2012, 29(11): 92-97. |
| [7] | 黄美灵, 陆百川. 基于种群小生境粒子群优化算法的交叉路口多相位信号配时优化[J]. 信息与控制, 2011, 40(1): 115-119, 123. Huang M L, Lu B C. Optimization of multiphase traffic signal timing at intersection based on species niching particle swarm optimization algorithm[J]. Information and Control, 2011, 40(1): 115-119, 123. |
| [8] | 沈国江, 孙优贤. 基于相序优化的多相位模糊交通控制[J]. 控制与决策, 2002, 17(z1): 654-658, 663. Shen G J, Sun Y X. Multi-phase fuzzy traffic control based on phase sequencer[J]. Control and Decision, 2002, 17(zl): 654-658, 663. |
| [9] | 温凯歌, 曲仕茄, 张玉梅. 城市单交叉口信号多相位自适应控制模型[J]. 系统仿真学报, 2009, 21(10): 3066-3070. Wen K G, Qu S R, Zhang Y M. Multiphase traffic signal adaptive controlling model for urban isolated intersection[J]. Journal of System Simulation, 2009, 21(10): 3066-3070. |
| [10] | 徐勋情, 黄卫. 单路口交通信号多相位实时控制模型及其算法[J]. 控制理论与应用, 2005, 22(3): 413-416, 422. Xu X Q, Huang W. Multiphase traffic signal real-time controlling model of isolated intersection and its algorithm[J]. Control Theory & Applications, 2005, 22(3): 413-416, 422. |
| [11] | 高海军, 李灵犀, 陈龙. 交通路口可变相位信号控制[J]. 交通运输工程学报, 2003, 3(3): 79-83. Gao H J, Li L X, Chen L. Changeable phases signal control of traffic intersection[J]. Journal of Traffic and Transportation Engineering, 2003, 3(3): 79-83. |
| [12] | 赵忠杰, 刘小强, 谢光秋. 单交通路口变相位变周期信号控制[J]. 长安大学学报: 自然科学版, 2005, 25(6): 70-72. Zhao Z J, Liu X Q, Xie G Q. Changeable phases and changeable periods signal control at traffic intersection[J]. Journal of Chang'an University: Natural Science Edition, 2005, 25(6): 70-72. |
| [13] | 陈智, 刘小明, 刘文婷, 等. 过饱和交叉口交通信号模糊关联控制方法[J]. 信息与控制, 2014, 43(3): 374-380. Chen Z, Liu X M, Liu W T, et al. Interconnected control of traffic signals at oversaturated intersections using fuzzy control method[J]. Information and Control, 2014, 43(3): 374-380. |
| [14] | Liu H X, Wu X, Ma W, et al. Real-time queue length estimation for congested signalized intersections[J]. Transportation Research, Part C: Emerging Technologies, 2009, 17(4): 412-427. |
| [15] | Zheng X, Recker W. An adaptive control algorithm for traffic-actuated signals[J]. Transportation Research, Part C: Emerging Technologies, 2013, 30(s1): 93-115. |
| [16] | 陈娟, 胡庆松. 城市过饱和路网的非均匀自适应相容优化控制[J]. 信息与控制, 2012, 41(5): 637-643. Chen J, Hu Q S. Non-even adaptive compatible optimization control for urban oversaturated traffic network[J]. Information and Control, 2012, 41(5): 637-643. |
| [17] | 李秀平, 刘智勇, 吴今培. 平面交叉路口的神经网络自学习控制方案[J]. 信息与控制, 2001, 30(1): 76-79. Li X P, Liu Z Y, Wu J P. An approach of intersection traffic signal control[J]. Information and Control, 2001, 30(1): 76-79. |
| [18] | 陈峻, 张国良, 徐良杰, 等. 交通管理与控制[M]. 北京: 人民交通出版社, 2012. Chen J, Zhang G L, Xu L J, et al. Traffic management and control[M]. Beijing: China Communications Press, 2012. |
| [19] | 王殿海. 交通流理论[M]. 北京: 人民交通出版社, 2002. Wang D H. Traffic flow theory[M]. Beijing: China Communications Press, 2002. |
| [20] | Slobodan G, Gordana S, Bratislav L. Optimal traffic control: Urban intersections[M]. CRC Press, 2008. |



