2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
1 引言
随着机器人技术和人机协作的发展,谐波齿轮传动和关节力矩传感器在机器人中得到越来越多的应用,由此带来的关节柔性使得刚性连杆—刚性关节的假设不再适用. 柔性关节机器人具有更复杂的动力学特性,柔性、 非线性、 强耦合和摩擦等因素严重制约了系统性能,对其使用传统的刚性机器人控制器无法取得良好效果,需要研究针对柔性关节机器人的控制. 目前常见的控制方法主要有奇异摄动、 积分流形、 无源法、 滑模控制、 反步法、 模糊控制、 神经网络等[1]. 按照控制器对系统建模的要求不同可以分为两类:
(1) 控制器不需要精确模型,不进行精确建模. 例如使用模糊控制器[2, 3]、 正交基函数的线性组合[4]和神经网络控制器[5, 6]等来逼近动力学系统中的非线性部分、 未知项和扰动项,从而应对模型不确定性和保证系统鲁棒稳定性. 这些方法分别在单连杆和2DOF、 4DOF平面柔性关节机器人上进行了验证. 然而随着机器人关节数目增加,函数逼近的计算复杂度也迅速上升. 文[7, 8]则是设计不包含机器人动力学的带重力补偿的比例微分(PD)控制器,文[8]设计的基于关节力矩反馈的PD无源控制器在6DOF柔性关节机器人上进行试验. 由于机器人的非线性特性,其轨迹跟踪性能难以保证.
(2) 控制器需要精确动力学模型. 常用的Spong模型将谐波建模为弹簧模型,忽略了连杆和关节动力学的耦合、 传动回差以及关节摩擦等,对模型简化过多,更精确的模型需要对关节柔性、 传动回差和非线性摩擦等进行建模[9, 10, 11, 12]. 目前针对单连杆柔性关节机器人的控制研究较多,文[13]采用Spong模型,设计振动力矩反馈PD控制器; 文[14]引入随机干扰建立随机动力学模型,设计自适应动态面控制器; 文[15]中采用静态摩擦模型,设计前馈加反馈的鲁棒控制器; 文[16]考虑LuGre动态摩擦模型和传动回差,设计自适应反步法控制器. 对于2DOF平面机器人,文[17]建立基于功能原理的动态摩擦模型,设计带摩擦补偿和关节柔性补偿的奇异摄动控制器. 对多连杆柔性关节机器人的控制器研究较少,且通常连杆数目越多,采用的模型越简化.
为实现高精度运动控制,本文在对多连杆柔性关节机器人建模时考虑了连杆和关节动力学的耦合项、 动态摩擦模型和关节回差,以建立更完整准确的动力学模型. 在此基础上设计自适应反步法控制器,并对不可测项进行在线估计和补偿,保证系统稳定性和良好的跟踪性能.
2 柔性关节机器人建模 2.1 n连杆柔性关节机器人动力学建模对n连杆柔性关节机器人进行分析,将与连杆转动速度相同的部件作为连杆部分,与电机转子转动速度相同的部件作为关节部分. 定义连杆i坐标系和关节i坐标系分别为固定在连杆i上和固定在关节i上的局部坐标系,其z轴同为关节i的旋转轴.
连杆i的动能为
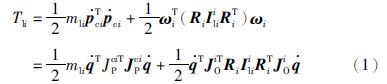
关节i的动能为
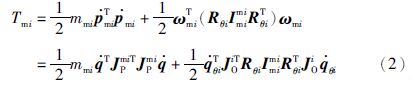
n连杆柔性关节机器人总动能为
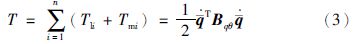
总重力势能为
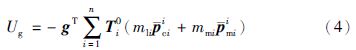
柔性关节机器人弹性势能主要由谐波传动、 力矩传感器的弹性形变带来. 总弹性势能为
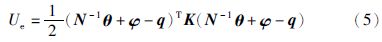
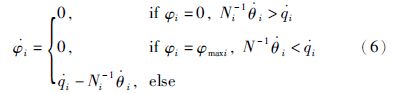
柔性关节机器人受到的对应于的广义力为
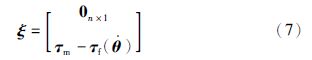
采用LuGre模型来描述摩擦,它将摩擦描述为两个刚体的表面通过有弹性的刚毛接触,摩擦力由刚毛的弹性变形产生[19]. LuGre模型包括了库仑力、 静摩擦力、 粘滞摩擦力、 Stribeck特性和粘—滑摩擦特性,是目前最完整的摩擦模型. 在该模型中,摩擦力矩是连续且动态变化的,不会像大部分静态模型那样在速度过零处发生突变,且能反映低速下的爬坡现象,更符合真实情况. 而且它使用统一的而非分段的模型来同时描述摩擦的静态和动态特性,便于理论分析. 关节摩擦模型如下:
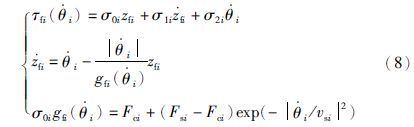
根据拉格朗日方程,有: 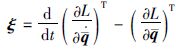 ,其中,L=T-Ug-Ue. 则根据式(3)、 (4)、 (5)、 (7)可得n连杆柔性关节机器人完整的动力学模型为
,其中,L=T-Ug-Ue. 则根据式(3)、 (4)、 (5)、 (7)可得n连杆柔性关节机器人完整的动力学模型为
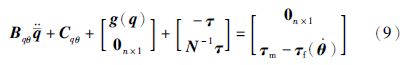
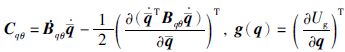 2.2 模型分析和简化
2.2 模型分析和简化由式(9)可以看出,连杆部分动力学和关节部分动力学之间存在复杂的非线性耦合项Bqθ和Cqθ.
首先对Bqθ进行分析. 式(2)中关节i坐标系相对于基坐标系的旋转矩阵Rθi可表示为Rθi=RiRmii,其中Rmii=rotz(θi-qi)为关节i坐标系相对于连杆i坐标系的旋转矩阵. 通常关节部分的惯量是关于旋转轴对称的,即Imimi=diag(Imixmi,Imixmi,Imizmi),则简单计算可知RmiiImimiRmiiT=Imimi,故有RθiImimiRTθi=RiImimiRTi.
而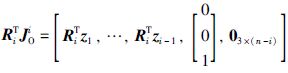 ,计算可得:
,计算可得:
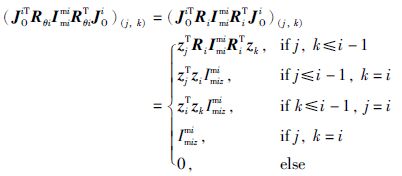
因此根据式(1)~(3)可得矩阵Bqθ的各个元素为
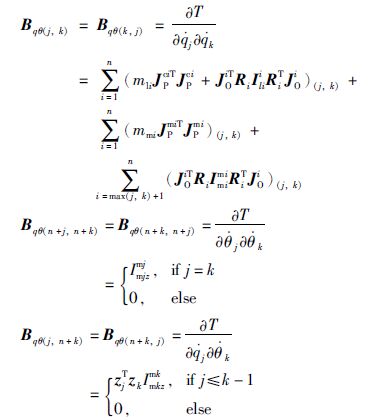
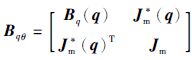 ,注意到它是q的函数,与θ无关. 可推出Cqθ为q、 ${\dot q}$和${\dot \theta }$的函数,可简写为
,注意到它是q的函数,与θ无关. 可推出Cqθ为q、 ${\dot q}$和${\dot \theta }$的函数,可简写为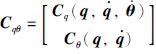 .
.
因此式(9)所示动力学模型可简写为如下形式:
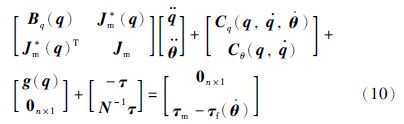
对于某些特殊构型的机械臂,动力学模型还可以进一步简化,例如对于平面机械臂,以及各关节的旋转轴始终相互垂直或平行的三维机械臂,有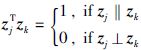 ,此时Jm*(q)为常数矩阵,且Cθ(q,)=0,Cq(q,${\dot q}$,${\dot \theta }$)为q和${\dot q}$的函数,与${\dot \theta }$无关,其连杆部分和关节部分不存在非线性耦合项,此处不再详述.
,此时Jm*(q)为常数矩阵,且Cθ(q,)=0,Cq(q,${\dot q}$,${\dot \theta }$)为q和${\dot q}$的函数,与${\dot \theta }$无关,其连杆部分和关节部分不存在非线性耦合项,此处不再详述.
由于常用的奇异摄动类方法要求关节刚度足够大,为避免这一限制,采用反步法设计控制器. 而反步法对不确定性敏感[20],需要对LuGre摩擦、 回差以及关节和连杆耦合项设计观测器,进行在线估计补偿,以保证系统稳定.
3.1 反步法控制器设计
令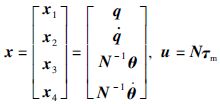 ,将式(10)所示柔性关节机器人动力学模型改写为状态空间形式,可得:
,将式(10)所示柔性关节机器人动力学模型改写为状态空间形式,可得:
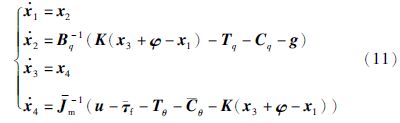
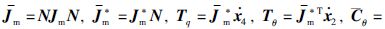
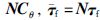 .
.
定义状态量xi的期望值(即虚拟控制量)为xid,定义状态跟踪误差为ei=xi-xid. 下面使用反步法设计原则依次设计虚拟控制量x2d、 x3d、 x4d,直至控制量u.
步骤1: 柔性关节机器人位置控制的目标是使连杆转角跟踪期望轨迹,因此有x1d=qd. 由式(11)可以得到跟踪误差e1的导数为
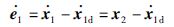
设计虚拟控制量x2d使e1稳定:
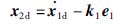

步骤2: 根据式(11)对跟踪误差e2求导可得:
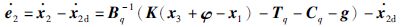
设计虚拟控制量x3d使e2稳定:
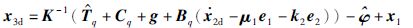
定义估计误差=${\bar \varphi }$,${\bar T}$q=${\hat T}$q-Tq,则有:
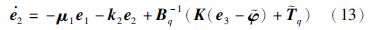
步骤3: 根据式(11)对跟踪误差e3求导可得:
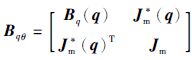
设计虚拟控制量x4d使e3稳定:
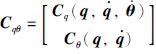
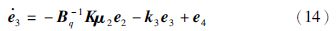
步骤4: 根据式(11)对跟踪误差e4求导可得
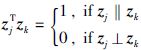
设计控制器u使e4稳定:
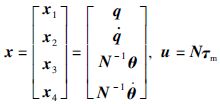
定义估计误差${\bar T}$θ=${\hat T}$θ-Tθ,${\bar \tau }$f=${\bar \tau }$f-${\bar \tau }$f,则有:
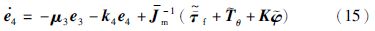
以下分别对反步法控制器设计中用到的耦合项、 摩擦力矩和回差的估计值${\hat T}$q、 ${\hat T}$θ、 ${\bar \tau }$f和${\hat \varphi }$设计观测器.
耦合项Tq和Tθ与角加速度有关,通常角加速度不可测或测量噪声很大,因此耦合项不能直接得到,需要对其进行估计. 根据式(11)设计耦合项的观测器如下:
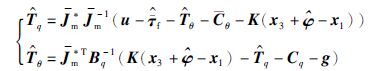
联立求解可得:
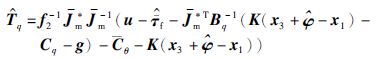
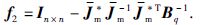
则估计误差为:
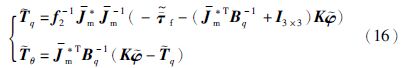
可以看出耦合项估计误差的大小取决于摩擦力矩和回差项的估计误差.
定义如下李亚普诺夫候选函数:
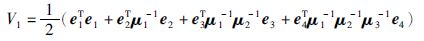
对其求导,并将式(12)~(16)代入可得:
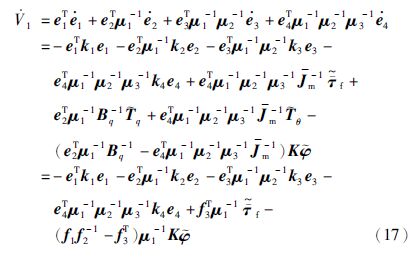
其中,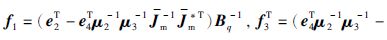
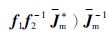 .
.
LuGre摩擦模型是一个含有不可测内部状态量zf的非线性模型,由于zf在速度较高时刚度很大,对其使用普通的卡尔曼型观测器会出现震荡. 为了获得稳定的摩擦估计,参考文[21]的方法,根据式(8)和式(17)设计如下双观测器:
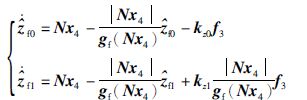
设计摩擦估计值为
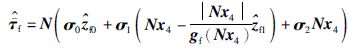
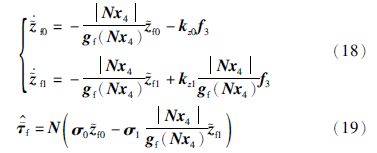
根据式(6)和式(17)对回差φ设计观测器:
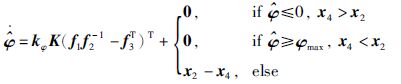
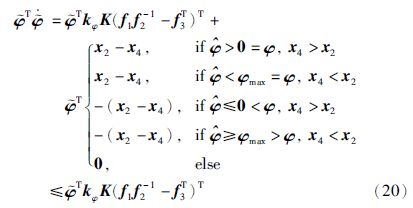
定义李亚普诺夫函数:
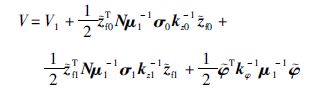
对其求导,并将式(17)~(20)代入可得:
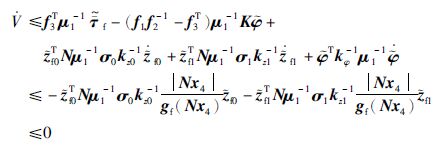
因此所设计的带观测器的反步法控制器能够使柔性关节机器人系统闭环稳定,且观测误差${\bar z}$f0、 ${\bar z}$f1和${\bar \varphi }$均收敛. 根据式(19)可以看出,由${\bar z}$f0和${\bar z}$f1收敛可得${\bar \tau }$f收敛; 根据式(16)可以看出,由${\bar \tau }$f和${\bar \varphi }$收敛可得${\bar T}$q收敛,进而由${\bar T}$q和${\bar \varphi }$收敛得出θ收敛,因此所设计的观测器是收敛的.
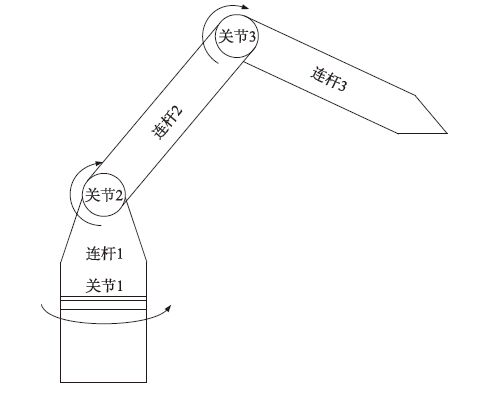
4 仿真算例为验证所设计控制方法的有效性,对如图 1所示的3DOF柔性关节机器人进行仿真,机器人动力学参数为
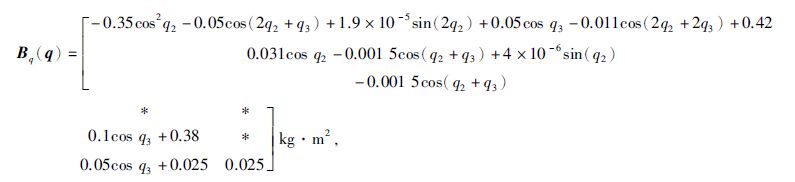
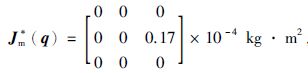 ,
g(q)=[0,-1.6sin(q2+q3)-14.2sin q2,
-1.6sin(q2+q3)]T N·m,
K=diag(5,5,6)×103 N·m/rad,
N=diag(80,80,80),
φmax=[0.01,0.01,0.01]T×π/180 rad,
Fc=[0.011,0.011,0.005 5]T N·m,
Fs=[0.017,0.017,0.008 7]T N·m,
vs=[0.06,0.06,0.06]T rad/s,
σ0=[0.5,0.5,0.25]T N·m/rad,
σ1=[4.6,4.6,2.3]T×10-3 N·m·s/rad,
σ2=[3.7,3.7,1.8]×10-4 N·m·s/rad.
,
g(q)=[0,-1.6sin(q2+q3)-14.2sin q2,
-1.6sin(q2+q3)]T N·m,
K=diag(5,5,6)×103 N·m/rad,
N=diag(80,80,80),
φmax=[0.01,0.01,0.01]T×π/180 rad,
Fc=[0.011,0.011,0.005 5]T N·m,
Fs=[0.017,0.017,0.008 7]T N·m,
vs=[0.06,0.06,0.06]T rad/s,
σ0=[0.5,0.5,0.25]T N·m/rad,
σ1=[4.6,4.6,2.3]T×10-3 N·m·s/rad,
σ2=[3.7,3.7,1.8]×10-4 N·m·s/rad.
|
| 图 1 3DOF柔性关节机器人 Fig. 1 3DOF flexible joint robot |
控制器参数设为: k1=diag(500,1 000,2 000),k2=k3=diag(50,100,200),k4=diag(0.5,1,2),μ1=diag(10,10,10),μ2=diag(1,1,0.1)×10-5,μ3=diag(0.01,0.01,0.01),kz0=diag(1,1,0.1)×10-10,kz1=diag(1,1,0.1)×10-14,kφ=diag(1,1,0.1)×10-18.
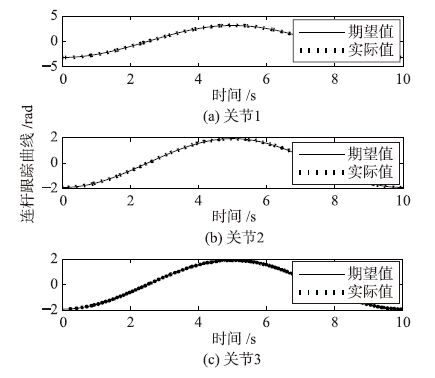
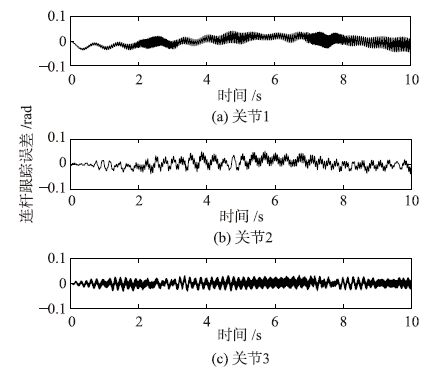
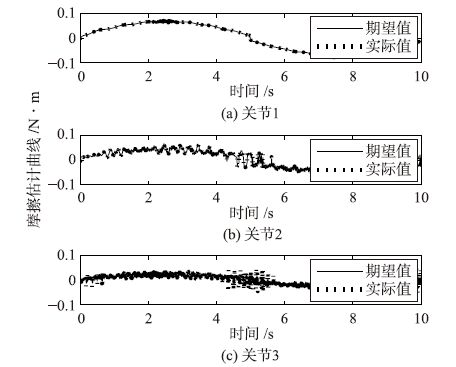
令机器人期望轨迹为各关节角最大运动范围的正弦曲线,关节1运动范围±180°,关节2和关节3运动范围±110°. 使用本文设计的控制方法进行仿真,得到连杆跟踪曲线如图 2所示,跟踪误差如图 3所示,3个连杆位置跟踪的均方根误差分别为0.018 9 rad、 0.016 7 rad和0.012 3 rad. 可以看出,连杆转角能够很好地跟踪期望值,跟踪误差有一定的抖动,其低频抖动主要受控制器输出限制的影响,高频部分则与关节刚度和连杆惯量等因素有关,3个连杆的高频振动分别为18.7 Hz、 18.7 Hz和80.2 Hz. 摩擦估计曲线如图 4所示,其均方根误差分别为5.6×10-6 N·m、 1.8×10-3 N·m和3.5×10-3 N·m. 3个关节回差估计的均方根误差分别为1.7×10-6 rad、 2.4×10-6 rad和6.4×10-6 rad. 耦合项Tq和Tθ估计的均方根误差分别为0.049 N·m和0.033 N·m. 可以看出,所设计的观测器能够很好地估计摩擦力矩、 关节回差和耦合项.
|
| 图 2 连杆转角跟踪曲线 Fig. 2 Tracking trajectory of the linkage rotation angle |
|
| 图 3 连杆转角跟踪误差 Fig. 3 Tracking errors of the linkage rotation angle |
|
| 图 4 摩擦估计曲线 Fig. 4 Estimates of the friction |
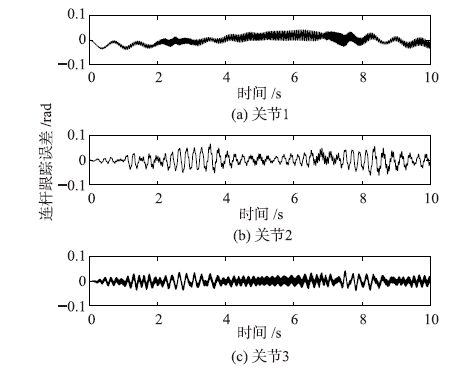
为检验关节刚度对控制器性能的影响,增大关节刚度为: K=diag(6,6,7)×103 N·m/rad,不改变控制器参数,则仿真结果如图 5所示,3个连杆位置跟踪的均方根误差分别为0.017 6 rad、 0.021 4 rad和0.013 2 rad. 可以看出,连杆转角依然能够很好地跟踪期望值,由于没有重新调节控制器参数,跟踪误差比之前的略大,而受控制器影响较大的低频抖动频率变化不大. 3个连杆的高频振动分别为20.2 Hz、 20.2 Hz和86.7 Hz,符合关节刚度越大,振动频率越高的原理.
|
| 图 5 改变关节刚度后连杆转角跟踪误差 Fig. 5 Tracking errors of the linkage rotation angle with changed joint stiffness |
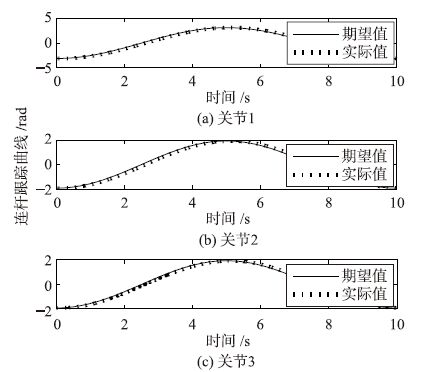
对比文[7]给出的通用的带重力补偿的PD控制器,该方法使用关节转角进行PD控制,避免了采用连杆转角反馈会带来的系统震荡发散[1],并使用连杆转角计算重力补偿,得到关节转角的期望值,因而能实现稳态误差为0的连杆位置跟踪. 仿真结果如图 6和图 7所示,3个连杆的均方根误差分别为0.160 4 rad、 0.099 3 rad和0.092 1 rad. 可以看出,该控制器能够保证系统稳定,但由于采用关节转角反馈进行PD控制,且未考虑系统动力学特性,在关节柔性和回差等因素影响下,连杆位置无法实时跟踪期望轨迹,且其动态跟踪误差与连杆位置以及期望角速度相关.
|
| 图 6 使用带重力补偿的PD控制器的连杆转角跟踪曲线 Fig. 6 Tracking curves of the linkage rotation angle with a PD controller with gravity compensation |
|
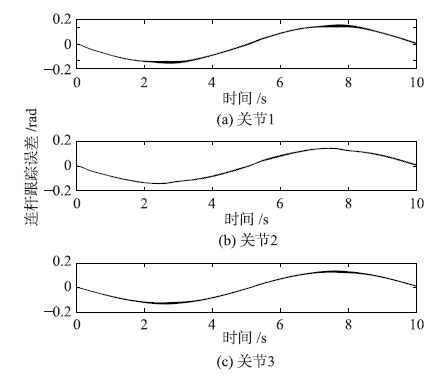
| 图 7 使用带重力补偿的PD控制器的连杆转角跟踪误差 Fig. 7 Tracking errors of the linkage rotation angle with a PD controller with gravity compensation |
本文对多连杆柔性关节机器人进行动力学分析,没有采用常见的Spong简化模型,而是考虑了回差对关节力矩的影响,以及关节部分和连杆部分之间复杂的耦合关系,并对摩擦采用能够充分描述其连续、 动态、 非线性特性的LuGre模型建模,得到更完整的柔性关节机器人动力学模型. 然后采用反步法设计控制器,并对摩擦、 回差和耦合项设计观测器进行在线估计补偿,实现稳定的高精度位置控制. 在一个3DOF柔性关节机器人上进行验证,仿真结果表明该方法能够准确进行估计补偿,减小连杆跟踪误差,适用于多连杆柔性关节机器人运动控制.
| [1] | Ozgoli S, Taghirad H D. A survey on the control of flexible joint robots[J]. Asian Journal of Control, 2006, 8(4): 1-15. |
| [2] | 张晓东, 贾庆轩, 孙汉旭, 等. 空间机器人柔性关节轨迹控制研究[J]. 宇航学报, 2008, 29(6): 1865-1870. Zhang X D, Jia Q X, Sun H X, et al. The research of space robot flexible joint trajectory control[J]. Journal of Astronautics, 2008, 29(6): 1865-1870. |
| [3] | Chaoui H, Gueaieb W. Type-2 fuzzy logic control of a flexible-joint manipulator[J]. Journal of Intelligent and Robotic Systems, 2008, 51(2): 159-186. |
| [4] | Huang A C, Chen Y C. Adaptive sliding control for single-link flexible-joint robot with mismatched uncertainties[J]. IEEE Transactions on Control Systems Technology, 2004, 12(5): 770-775. |
| [5] | Yen H M, Li T H S, Chang Y C. Adaptive neural network based tracking control for electrically driven flexible-joint robots without velocity measurements[J]. Computers and Mathematics with Applications, 2012, 64(5): 1022-1032. |
| [6] | 陈志勇, 郭益深, 陈力. 柔性关节双臂空间机器人的滑模神经网络控制[J]. 系统仿真学报, 2014, 26(12): 2950-2956. Chen Z Y, Guo Y S, Chen L. Sliding-mode neural network control of flexible-joint dual-arm space robot[J]. Journal of System Simulation, 2014, 26(12): 2950-2956. |
| [7] | Tomei P. A simple PD controller for robots with elastic joints[J]. IEEE Transactions on Automatic Control, 1991, 36(10): 1208-1213. |
| [8] | Albu-Schaffer A, Ott C, Hirzinger G. A unified passivity-based control framework for position, torque and impedance control of flexible joint robots[J]. International Journal of Robotics Research, 2007, 26(1): 23-39. |
| [9] | Ruderman M, Hoffmann F, Bertram T. Modeling and identification of elastic robot joints with hysteresis and backlash[J]. IEEE Transactions on Industrial Electronics, 2009, 56(10): 3840-3847. |
| [10] | Tjahjowidodo T, Al-Bender F, Van Brussel H. Theoretical modelling and experimental identification of nonlinear torsional behaviour in harmonic drives[J]. Mechatronics, 2013, 23(5): 497-504. |
| [11] | Albu-Schaffer A, Bertleff W, Rebele B, et al. ROKVISS-Robotics component verification on ISS current experimental results on parameter identification[C]//2006 IEEE International Conference on Robotics and Automation. Piscataway, NJ, USA: IEEE, 2006: 3879-3885. |
| [12] | 张奇, 刘振, 谢宗武, 等. 具有谐波减速器的柔性关节参数辨识[J]. 机器人, 2014, 36(2): 164-170. Zhang Q, Liu Z, Xie Z W, et al. Parameters identification of flexible joints with harmonic driver[J]. Robot, 2014, 36(2): 164-170. |
| [13] | 郭闯强, 倪风雷, 孙敬颋, 等. 具有力矩传感器的柔性关节的振动抑制[J]. 机器人, 2011, 33(4): 449-454. Guo C Q, Ni F L, Sun J T, et al. Vibration suppression for the flexible joint with torque sensor[J]. Robot, 2011, 33(4): 449-454. |
| [14] | 刘振国, 武玉强. 随机激励下单杆柔性关节机械臂的建模与控制[J]. 控制理论与应用, 2014, 31(8): 1105-1110. Liu Z G, Wu Y Q. Modeling and control for single-link flexible-joint arm with random disturbances[J]. Control Theory and Applications, 2014, 31(8): 1105-1110. |
| [15] | 党进, 倪风雷, 刘业超, 等. 基于新型补偿控制策略的柔性关节控制器设计[J]. 机器人, 2011, 33(1): 150-155. Dang J, Ni F L, Liu Y C, et al. Design for flexible joint controller based on a new compensation control strategy[J]. Robot, 2011, 33(1): 150-155. |
| [16] | Wang X Z, Li H Y, Wang Y C, et al. Adaptive backstepping control of flexible joint robots with friction compensation based on LuGre model[C]//26th Chinese Control and Decision Conference. Piscataway, NJ, USA: IEEE, 2014: 1484-1489. |
| [17] | Salmasi H, Fotouhi R, Nikiforuk P N. A manoeuvre control strategy for flexible-joint manipulators with joint dry friction[J]. Robotica, 2010, 28(4): 621-635. |
| [18] | Siciliano B, Sciavicco L, Villani L, et al. Robotics-Modelling, planning and control[M]. Berlin, Germany: Springer, 2009. |
| [19] | Olsson H, Astrom K J, de Wit C C, et al. Friction models and friction compensation[J]. European Journal of Control, 1998, 4(3): 176-195. |
| [20] | 席雷平, 陈自力, 齐晓慧. 基于非线性干扰观测器的机械臂自适应反演滑模控制[J]. 信息与控制, 2013, 42(4): 470-477. Xi L P, Chen Z L, Qi X H. Adaptive backstepping sliding mode control for robotic manipulator with nonlinear disturbance observer[J]. Information and Control, 2013, 42(4): 470-477. |
| [21] | Yao J Y, Jiao Z X, Yao B. Robust control for static loading of electro-hydraulic load simulator with friction compensation[J]. Chinese Journal of Aeronautics, 2012, 25(6): 954-962. |



