2. 合肥工业大学经济学院, 安徽 合肥 230601
1 引言
永磁同步电机(permanent magnet synchronous motor，PMSM)以其噪声小、 结构简单、 可靠性高等优点已经被广泛应用于交流伺服系统中. 永磁同步电机模型具有非线性、 多变量等特点，当系统参数值位于某个范围时，系统会出现分叉、 极限环甚至混沌现象. 混沌现象的出现会严重损害电机的性能甚至会使系统崩溃，因此需要控制混沌现象的发生，现已有很多学者对混沌控制进行了研究[1, 2, 3, 4, 5, 6]. Yu等[7, 8]采用反步方法，设计模糊规则对系统非线性部分进行估计，设计模糊自适应控制器实现对永磁同步电机系统的控制.
自1965年美国学者Zadeh首次提出模糊集理论后，在控制领域，模糊逻辑控制一直受到广泛关注. 模糊控制方法与其他控制方法的有机结合，成功实现了对高度非线性和不确定复杂系统的有效控制[9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22]. Chen等[10]设计基于模糊逼近的自适应控制器，实现针对带有死区的非线性时滞系统的控制. Tong等[14, 15, 16]分别针对在传感器失灵情况下的大规模非线性系统和带有未建模可变信号的未知随机非线性系统，设计出模糊状态观测器用于估计系统不可测状态变量，实现对系统的自适应容错控制. 在各种模糊控制技术中，基于反步法的自适应模糊控制是一种有效的控制方法. 文[3, 7, 8, 15]基于模糊控制策略，针对不同系统构造自适应反步滑模控制器.
分数阶微积分和整数阶微积分一样，已有300余年的历史. 自1982年美籍法国数学家Mandelbrot首次提出自然界和许多技术学科存在大量分数维的事实后，国内外部分学者开始应用分数阶微积分解决大量实际问题. 分数阶微积分已经在材料力学、 生物物理学、 应用数学等方面得到了广泛应用[19, 20, 21, 22, 23]. 分数阶理论不仅为很多实际系统提供了新的数学工具，而且在一些实际复杂系统的建模过程中，采用分数阶微积分往往要比整数阶微积分更加精确. 但是，目前尚未实现通过反步方法和自适应模糊控制方法的有机结合对分数阶系统进行控制. 本文针对分数阶未知参数永磁同步电机系统，采用反步控制策略，同时结合模糊控制规则，实现系统信号对已知参考信号进行有效跟踪. 利用模糊逻辑系统逼近系统中的复杂分数阶函数，采用分数阶自适应率对系统中未知参数进行估计，设计自适应模糊控制器，保证跟踪误差渐近稳定. 同时，通过自适应模糊控制器与不带模糊系统的自适应控制器的比较，可以看出，自适应模糊控制器具有结构简单、 易于工程实现的特点. 实例仿真表明，所设计的模糊控制律可以确保系统较快地跟踪已知参考信号，且系统信号都有界.
2 预备知识Caputo分数阶积分定义为
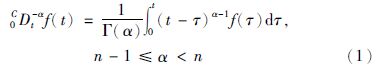
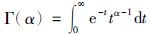为伽马函数. Caputo分数阶微分定义为
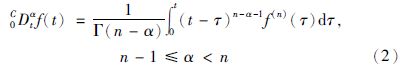
注1 分数阶微积分的定义有3种常见形式，分别由数学家Grunwald-Letnikov、 Riemann-Liouville(R-L)和Caputo等给出. Caputo的定义具有较好的物理意义，因此本文采用Caputo的定义形式.
引理1[23] 设x(t)∈Rn为连续可微函数，则
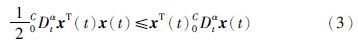
引理2[24] 设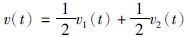
，其中
，x1i(t)，i=1，…，m1，x2j(t)，j=1，…，m2，具有连续的一阶导数. 若存在常数k>0使得
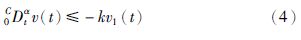
(a) x1i(t)和x2j(t)有界；
(b) x1i2(t)≤v(0)Eα，1(-ktα)；
(c) $\underset{t\to \infty }{\mathop{\lim }}\,{{x}_{li}}$(t)=0，i=1，…，m1.
模糊逻辑系统主要由知识库、 模糊化、 基于模糊规则的模糊推理和去模糊化4个部分构成，其中第i条模糊规则(i=1，2，…，N)的形式为： 如果x1(t)为F1i，x2(t)为F2i，…，xn(t)为Fni，那么$\hat{f}$(t)为Bji，这里x(t)=[x1(t)，x2(t)，…，xn(t)]T∈Rn和$\hat{f}$(t)∈R分别为模糊逻辑系统的输入和输出，Fi和Bi为R上的模糊集合. 模糊系统根据模糊规则把Rn上的模糊集合映射成R上的模糊集合. 模糊系统的输出可写成
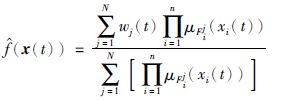
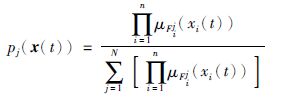
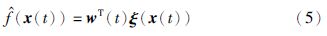
经过仿射和时间尺度变换后的均匀气隙永磁同步电动机数学模型为[25]
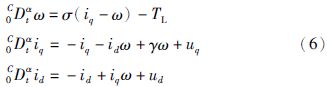
一般地，考虑永磁同步电动机空载运行一段时间后突然断电，各外部输入项为0的情形，即TL=uq=ud=0时，系统(6)变为如下形式：
|
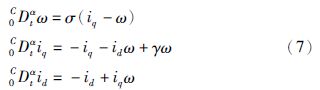
| 图 1 分数阶PMSM系统混沌吸引子 Fig. 1 Chaotic attractors of fractional-order PMSM system |
为了消除混沌现象，设计控制器uq和ud，添加在系统(7)中，为书写方便，记x1=ω，x2=iq，x3=id，可得到以下形式：
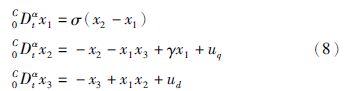
系统(8)的自适应反步控制器的设计过程如下：
第1步 对于已知参考信号xd，定义跟踪误差变量z1=x1-xd，对z2求α阶导数，同时利用式(8)中的第一个方程，显然有
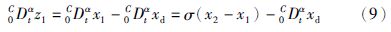
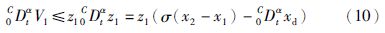
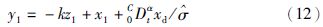
为虚拟控制变量，k>0是设计参数，σ>0是系统参数，$\hat{\sigma }$是σ的估计量. 令k1=σk，显然k1>0，于是
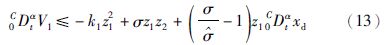
第2步 对z2求α阶导数，同时利用式(8)中的第二个方程，得
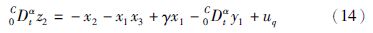
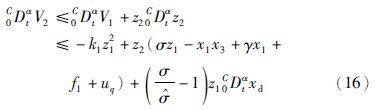
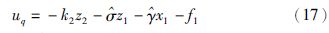
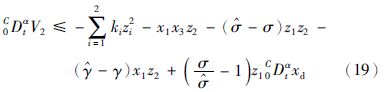
第3步 设z3=x3，并对z3求α阶导数，得
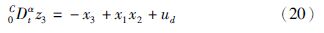
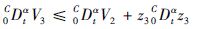
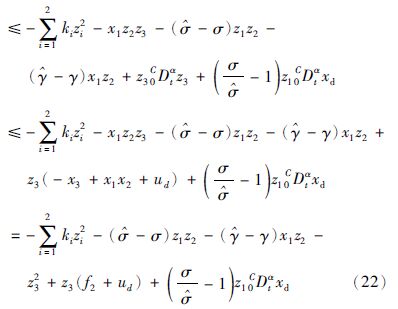
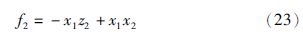
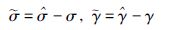
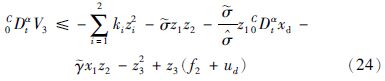
设计自适应控制器为
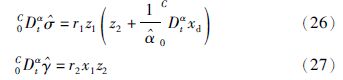
根据以上推理，有以下结论：
定理1 考虑系统(8)和已知参考信号xd，在控制器(17)、 (25)和分数阶参数自适应规则(26)、 (27)作用下，闭环控制系统跟踪误差渐近稳定，而且所有的闭环信号有界. <
证明 选择李亚普诺夫函数
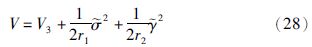
把式(25)代入式(24)，得
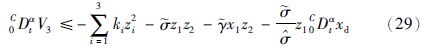
对V求α阶导数，得
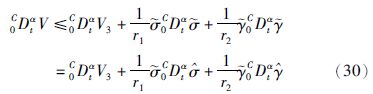
把自适应规则式(26)和式(27)代入式(30)，同时利
用式(29)，得
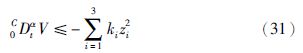
根据引理2，闭环控制系统跟踪误差渐近稳定，而且所有的闭环信号有界.
注2 设计的控制器(17)看似简单，其实是很复杂的，因为y1是变量x1、 z1、 0CDtαxd、 的函数，f1是变量x2、 0CDtαy1的函数，其结构相当复杂，因此实际设计这样的控制器是很困难的.
3.3 自适应模糊控制器的设计及稳定性分析混沌系统各状态变量是有界的，系统参数σ是有界正数，对于式(26)，适当选取初始条件，可以保证h1≤$\hat{\sigma }$≤h2，其中h1和h2是正常数. 显然0CDtαy1是连续且有界的，因此f1是连续有界函数，可以利用模糊逻辑系统有效逼近.
下面利用模糊系统逼近复杂函数f1，设计模糊控制器，实现系统信号对已知参考信号的有效跟踪. 根据模糊系统逼近原理，对任意常数ε>0，一定存在一个模糊逻辑系统wTξ，满足
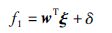
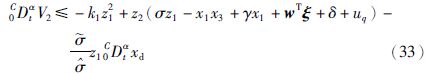
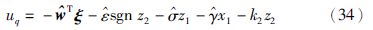
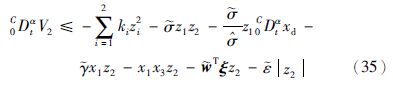
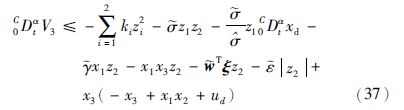
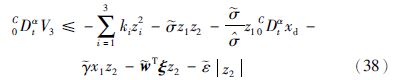
为了对模糊系统理想参数向量w以及模糊最优逼近误差上界ε进行有效估计，设计如下分数阶参数自适应规则
于是有以下结论：
定理2 考虑系统(8)和已知参考信号xd，在控制器(34)、 (25)和分数阶参数自适应规则(26)、 (27)、 (39)、 (40)作用下，闭环控制系统跟踪误差渐近稳定，而且所有的闭环信号有界.
证明 选择李亚普诺夫函数
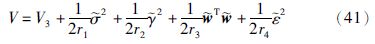
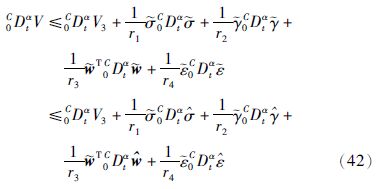
再利用式(26)、 式(27)、 式(39)和式(40)，得
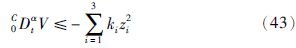
根据引理2，闭环控制系统跟踪误差渐近稳定，而且所有的闭环信号有界.
注3 容易看出，设计的控制器不含有系统运行参数σ和γ，因此无需预先知道系统运行参数σ和γ，仍然能对已知信号有效跟踪.
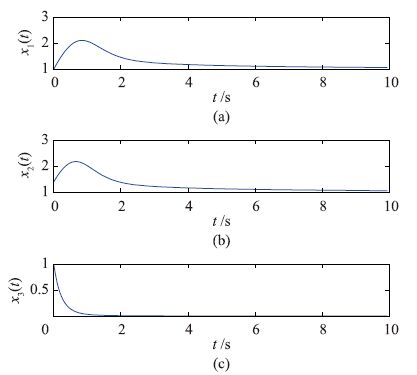
4 仿真分数阶永磁同步电机控制系统仿真框图见图 2. 系统信号初值设为x(0)=[1，1.4，1]T，已知转子机械角速度参考信号为xd=1. 控制器和自适应率设计参数分别为k1=5，k2=5，k3=1，γ1=0.5，γ2=1，γ3=2，γ4=1. 模糊系统逼近误差的估计值$\hat{\varepsilon }$(t)初值为$\hat{\varepsilon }$(0)=0.01. 在模糊控制器(34)、 (25)和分数阶参数自适应规则(26)、 (27)、 (39)、 (40)作用下，系统状态信号x1(t)，x2(t)和x3(t)随时间变化曲线如图 3所示，控制器以及系统参数估计随时间变化曲线如图 4所示. 从图 3可以看出，闭环控制系统状态信号是渐近稳定的，同时实现了系统信号x1(t)对已知参考信号xd有效跟踪. 从图 3和图 4可以看出，闭环控制系统所有信号都是有界的.
|
| 图 2 控制系统仿真框图 Fig. 2 Simulation diagram of control system |
|
| 图 3 系统状态变量曲线 Fig. 3 The curves of system state variables |
|
| 图 4 控制器以及系统参数估计曲线 Fig. 4 The curves of controllers and system parameter estimations |
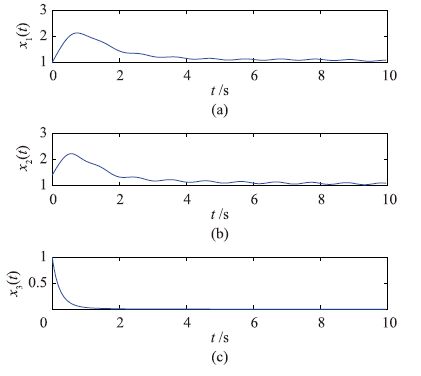
针对系统(8)，在系统参数σ、 γ上分别添加扰动0.2sin 5t，0.25sin 6t，同时增加负载0.2sin t，系统状态信号x1(t)，x2(t)，x3(t)，模糊控制器以及系统参数估计随时间变化曲线如图 5和图 6. 由图 5和图 6可知，在模糊控制器作用下，系统对已知参考信号的跟踪误差仍然是渐近稳定的，只是系统状态信号在收敛的过程中有一些小的波动，这种波动就是由系统参考信号的变化以及负载波动引起的，说明设计的模糊控制器具有较好的鲁棒性.
|
| 图 5 带有参数扰动和负荷的系统状态变量曲线 Fig. 5 The curves of system state variables with parameter disturbances and loads |
|
| 图 6 带有参数扰动和负荷的系统控制器以及系统参数估计曲线 Fig. 6 The curves of the system controllers and parameter estimations with parameter disturbances and loads |
针对未知运行参数的分数阶永磁同步电机混沌系统，基于分数阶李亚普诺夫稳定性理论，采用反步方法设计自适应模糊控制器和分数阶参数自适应律，实现了系统信号对已知参考信号的快速跟踪. 为了便于说明自适应模糊控制器的有效性，设计了不带模糊系统和带模糊系统的两种控制器，通过比较可以看出，自适应模糊控制器具有结构简单、 控制效果较好并有较好鲁棒性等特点. 同时，本文提出的控制方法适用于更广泛的分数阶非线性系统控制. 当分数阶永磁同步电机混沌系统中3个子系统的分数阶不同时，需要做进一步的研究.
| [1] | Lü J H, Murali K, Sinha S, et al. Generating multi-scroll chaotic attractors by thresholding[J]. Physics Letters A, 2008, 372(18): 3234-3239. |
| [2] | 方一鸣, 李智, 吴洋羊, 等. 基于终端滑模负载观测器的永磁同步电机位置系统反步控制[J]. 电机与控制学报, 2014, 18(9): 105-111. Fang Y M, Li Z, Wu Y Y, et al. Backstepping control of PMSM position systems based on terminal-sliding-mode load observer[J]. Electric Machines and Control, 2014, 18(9): 105-111. |
| [3] | 李宁. 一种混沌系统的改进反演自适应模糊控制[J]. 信息与控制, 2012, 41(6): 735-740. Li N. A modified backstepping adaptive fuzzy control for the chaotic system[J]. Information and Control, 2012, 41(6): 735-740. |
| [4] | 薛树功, 魏利胜, 凌有铸. 基于EKF和SMC的永磁同步电机无传感器矢量控制[J]. 信息与控制, 2012, 41(2): 267-272. Xue S G, Wei L S, Ling Y Z. Sensorless vector control of permanent magnet synchronous motors based on EKF and SMC[J]. Information and Control, 2012, 41(2): 267-272. |
| [5] | 杜仁慧, 吴益飞, 陈威, 等. 永磁同步电机伺服系统高精度自适应鲁棒控制[J]. 信息与控制, 2013, 42(1): 132-144. Du R H, Wu Y F, Chen W, et al. High accuracy adaptive robust control for permanent magnet synchronous motor systems[J]. Information and Control, 2013, 42(1): 132-144. |
| [6] | 蒋彦, 刘国海, 董蓓蓓, 等. 基于神经网络广义逆的PMSM模型参考自适应解耦控制器[J]. 信息与控制, 2013, 42(6): 58-663. Jiang Y, Liu G H, Dong B B, et al. Model reference adaptive decoupling controller based on neural network generalized inverse for PMSM[J]. Information and Control, 2013, 42(6): 658-663. |
| [7] | Yu J P, Chen B, Yu H S, et al. Adaptive fuzzy tracking control for chaotic permanent magnet synchronous motor drive system via back stepping[J]. Nonlinear Analysis: Real World Applications, 2011, 12(1): 671-681. |
| [8] | 于金鹏, 陈兵, 于海生, 等. 基于自适应模糊反步法的永磁同步电机位置跟踪控制[J]. 控制与决策, 2010, 25(10): 1547-1551. Yu J P, Chen B, Yu H S, et al. Adaptive fuzzy backstepping position tracking control for permanent magnet synchronous motor[J]. Control and Decision, 2010, 25(10): 1547-1551. |
| [9] | Yang Y, Hua C C, Guan X P. Adaptive fuzzy finite-time coordination control for networked nonlinear bilateral teleoperation system[J]. IEEE Transactions on Fuzzy Systems, 2014, 22(3): 631-641. |
| [10] | Chen B, Liu X P, Liu K F, et al. Fuzzy approximation-based adaptive control of nonlinear delayed systems with unknown dead zone[J]. IEEE Transactions on Fuzzy Systems, 2014, 22(2): 237-248. |
| [11] | Boulroune A, M'Saad M, Farza M. An adaptive fuzzy variable controller for multivariable nonlinear state time-varying delay systems subject to input nonlinearities[J]. Fuzzy Sets and Systems, 2011, 164(1): 45-65. |
| [12] | Boulkroune A, Tadjine M, M'Saad M. How to design a fuzzy adaptive controller based on observers for uncertain affine nonlinear systems[J]. Fuzzy Sets and Systems, 2008, 159(8): 926-948. |
| [13] | 李宁, 刘恒, 向伟. 带有控制输入扰动和死区的混沌系统自适应模糊控制[J]. 物理学报, 2012, 61(23): 230505. Li N, Liu H, Xiang W. Fuzzy adaptive tracking control of uncertain chaotic system with input perturbance and nonlinearity[J]. Acta Physica Sinica, 2012, 61(23): 230505. |
| [14] | Tong S C, Huo B Y, Li Y M. Observer-based adaptive decentralized fuzzy fault-tolerant control of nonlinear large-scale systems with actuator failures[J]. IEEE Transactions on Fuzzy Systems, 2014, 22(1): 1-15. |
| [15] | Tong S C, Wang T, Li Y M. Fuzzy adaptive actuator failure compensation control of uncertain stochastic nonlinear systems with unmodeled dynamics[J]. IEEE Transactions on Fuzzy Systems, 2014, 22(3): 563-574. |
| [16] | Tong S C, Li Y M. Adaptive fuzzy output feedback control of MIMO nonlinear systems with unknown dead-zone inputs[J]. IEEE Transactions on Fuzzy Systems, 2013, 21(1): 134-146. |
| [17] | Han S I, Lee J M. Fuzzy echo state neural networks and funnel dynamic surface control for prescribed performance of a nonlinear dynamic system[J]. IEEE Transactions on Industrial Electronics, 2014, 61(2): 1099-1112. |
| [18] | Xu Y, Tong S, Li Y. Prescribed performance fuzzy adaptive fault-tolerant control of non-linear systems with actuator faults[J]. IET Control Theory and Applications, 2014, 8(6): 420-431. |
| [19] | Huang X, Wang Z, Li Y, et al. Design of fuzzy state feedback controller for robust stabilization of uncertain fractional-order chaotic systems[J]. Journal of the Franklin Institute, 2015, 351(12): 5480-5493. |
| [20] | Zhong F, Li H, Zhong S, et al. An SOC estimation approach based on adaptive sliding mode observer and fractional order equivalent circuit model for lithium-ion batteries[J]. Communications in Nonlinear Science and numerical Simulation, 2015, 24(1/2/3): 127-144. |
| [21] | Lin T C, Kuo C H, Lee T Y, et al. Adaptive fuzzy H∞tracking design of SISO uncertain nonlinear fractional order time-delay systems[J]. Nonlinear Dynamics, 2012, 69(4): 1639-1650. |
| [22] | Lin T C, Lee T Y, Balas V E. Adaptive fuzzy sliding mode control for synchronization of uncertain fractional order chaotic systems[J]. Chaos Solitons & Fractals, 2011, 44(10): 791-801. |
| [23] | Aguila-Camacho N, Duarte-Mermoud M A, Gallegos J A. Lyapunov functions for fractional order systems[J]. Communications in Nonlinear Science and numerical Simulation, 2014, 19(9): 2951-2957. |
| [24] | 刘恒, 李生刚, 孙业国, 等. 带有未知非对称控制增益的不确定分数阶混沌系统自适应模糊同步控制[J]. 物理学报, 2015, 64(7): 070503. Liu H, Li S G, Sun Y G, et al. Adaptive fuzzy synchronization for uncertain fractional order chaotic systems with unknown nonsymmetrical control gain[J]. Acta Physics Sinica, 2015, 64(7): 070503. |
| [25] | Li C L, Yu S M, Luo X S. Fractional-order permanent magnet synchronous motor and its adaptive chaotic control[J]. Chinese Physics B, 2012, 21(10): 100506. |