2. 江南大学物联网工程学院自动化研究所, 江苏 无锡 214122
1 引言
现代工业过程中，基于数据驱动的软测量建模方法得到了越来越多的关注. 一些常用的软测量建模方法如偏最小二乘(partial least squares，PLS)[1, 2]、 主成分分析(principal component analysis，PCA)[3, 4]等能够很好地处理输入变量和输出变量之间的线性关系. 人工神经网络(artificial neural networks，ANN)[5]、 支持向量机(support vector machine，SVM)、 最小二乘支持向量机(least squares support vector machine，LS-SVM)[6, 7, 8, 9]能够有效地处理过程的非线性关系. 近年来，高斯过程回归(Gaussian process regression，GPR)作为一种非参数概率模型，不仅可以给出预测值，还可以得到预测值对模型的信任值[10, 11]. 这些建模方法虽可以有效地处理过程高度的非线性和输入输出之间高维的映射关系，但是这些数据模型往往都是假设建模误差符合高斯分布的基础上建立的. 事实上，工业过程中常常包含了不同的随机分布、 多样的测量散射和非测量输入(隐藏输入)，建模往往非常复杂[12]. 因此，一般认为误差分布符合单一高斯分布是一种比较严苛的假设，所建立的往往是局部优化的预测模型.
为了提高建模精度，用一种基于高斯混合模型(Gaussian mixture model，GMM)的建模策略提取隐含在预测误差中的信息. 由于GMM具有很强的数据处理能力，应用期望最大化算法求解其参数，因此在处理语音识别、 彩色图像检测、 模式分类和聚类分析方面得到越来越多的拓展应用[13, 14, 15]. Chen等人研究了有限GMM算法在概率密度估计和统计过程监控方面的应用，然而GMM算法用于对误差数据进行特征分析的研究却很有限. 只要GMM模型包含足够多的高斯成分，就能逼近任意合理的连续概率密度[12]. 因此，可以用GMM描述复杂非高斯模型的误差特征，通过加入训练数据的输出误差构建误差数据集，建立误差高斯混合模型(error Gaussian mixture model，EGMM)，通过对从EGMM提取出来的信息进行检验假设或者数据模型改进，从而能提高建模的精度.
因此，需要用合适的相关变量构建一个概率EGMM模型，从而使隐含在预测误差中的复杂的概率特征能够被提取出来，以达到提高模型精度的目的. 通过EGMM模型，对于一个新的输入，可以计算得到误差的概率密度函数、 均值和方差. 误差方差可用来评估模型预测输出值的可靠性，用来决定当前模型是否需要更新，从而根据当前过程的动态变化产生一个自适应的软测量模型. 误差均值可以用来对这个新的输入的预测输出值进行补偿，从而提高模型预测输出的精度. 同时为了对过程变量进行降维，解决不同变量之间很强的相关性，利用传统的PCA方法对过程变量进行分析. 然后基于得分变量，建立GPR模型. 将本文所提方法用于一个典型的数值仿真及过程工业SRU的H2S浓度预测，通过仿真实验表明，基于EGMM的GPR建模相比较于传统的GPR建模具有更高的精度，EGMM能从预测误差中提取十分重要的信息.
2 预备知识 2.1 主成分分析(PCA)给定训练数据X∈RD×N，D是过程变量的维数，N是训练数据的个数. PCA是在X的协方差矩阵基础上实现的. 一般情况下，可以通过奇异值分解(singular value decomposition，SVD)的方法建模PCA模型[16]. 假设PCA模型有Q个主成分，X可以被分解为如下形式[16]：
GPR[17]是一种基于高斯随机函数的机器学习方法. 对于任意一个给定的输入，利用GPR可以得到关于对应输出的一个高斯分布. 给定训练样本集X∈RD×N和y∈RN，其中，y=(yi，i=1，…，N)和X=(xi，i=1，…，N)分别代表维的输入和输出数据. 输入和输出之间的关系由式(2)产生：
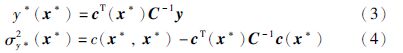
GPR可以选择不同的协方差函数c(xi，xj)产生协方差矩阵Σ，只要选择的协方差函数能保证产生的协方差矩阵满足非负正定的关系. 本文选择高斯协方差函数：
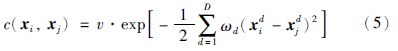
需要对式(5)中的未知参数v，ω1，…，ωD和高斯噪声方差σn2的值进行估计，一般最简单的方法就是通过极大似然估计得到参数.
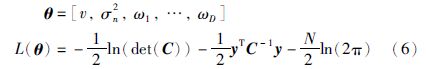
为了求得参数θ的值，首先将参数θ设置为一个合理范围内的随机值，然后用共轭梯度法得到优化的参数[18]. 获得最优参数θ后，对于测试样本x*，可以用式(3)和式(4)来估计GPR模型的输出值.
3 采用EGMM校正的GPR软测量建模 3.1 高斯混合模型(GMM)对于任意一个新的数据，当其不符合高斯分布时，单个高斯成分往往不能有效地描述其概率特征. 当高斯成分的数目足够多时，GMM能够拟合任意概率密度. 假设训练样本X=(xi，i=1…N)是独立同分布的，数据X的概率密度函数可以表示为
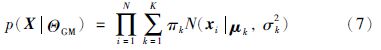
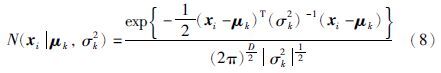
基于训练样本数据，高斯成分的分布参数μk、 σk2和πk可以通过期望最大化算法(expectation-maximization，EM)[17]估计得到.
3.2 基于GMM的条件误差均值和方差的计算由于模型预测误差中常常包含了丰富的有用信息，因此可以从误差数据中提取有用信息对模型预测输出进行校正. 本文通过构建误差数据的EGMM模型，从而提取有用信息条件误差均值和方差. 基于EGMM的GPR软测量建模方法，首先需要确定合适的误差数据和高斯成分的数目K. 一般误差数据是由GPR模型的输入变量和模型的输出误差组成[12]. 给定训练样本集X∈RD×N和y∈RN，其中X=(xi，i=1，…，N)，y=(yi，i=1，…，N)，分别代表D维的输入和输出数据. 在用PCA对输入变量进行降维处理之前需要对数据进行标准化处理，得到标准化数据集用于建立PCA模型，然后得到得分矩阵T=(ti∈RQ，i=1，…，N)，Q<D表示所选择的主成分的数目. 基于得分矩阵T和输出向量y=(yi，i=1，…，N)建立GPR模型：
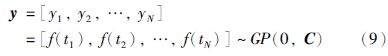
由于任意一个样本数据xe=[t，e]T∈RQ+1服从非高斯分布，一个单独的高斯分布不能有效地描述其概率特征. 选择合适数目的高斯成分，根据GMM算法的建模步骤，关于xe的概率密度函数可以表示为[17]
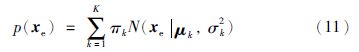
通过建立EGMM模型可以计算得到每个高斯成分k的均值向量μk和方差矩阵Σk：
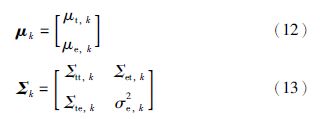
可以估计得到每个高斯成分的条件误差均值μe|t，k和条件误差方差σ2e|t，k[15]：
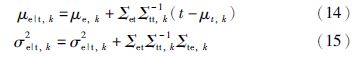
基于式(14)和式(15)，可估计得到K个混合高斯成分的条件误差均值μe|t和条件误差方差σ2e|t：
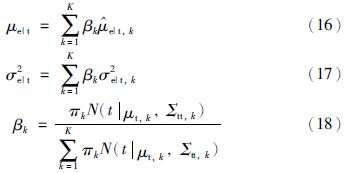
然而EGMM模型的建立需要选择合适数目的高斯成分，高斯成分的个数K选择不能过大，太大会导致误差数据的过拟合，选择过小会导致误差数据拟合不够. GMM模型的优化，可以采用一些性能标准，包括Akaike信息准则[19]和贝叶斯信息准则(Bayesian information criterion，BIC)[20]. 对于GMM模型，BIC算法可以优化得到更好的结构平衡，因此本文选择如式(19)所示的BIC作为性能标准决定最优化的高斯成分的个数K.
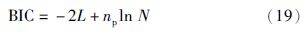
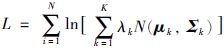表示对数似然函数，np表示K个高斯成分所具有的自由参数的个数，N表示训练数据集中数据的个数.
条件误差方差σ2e|t可用来对GPR模型的预测表现性能进行评估，条件误差均值μe|t表明任意特定的输出是否有偏差. 因此，可以用μe|t对预测输出进行校正从而提高预测精度. 软测量模型最终校正的预测输出${\hat{y}}$cor(xnew)为
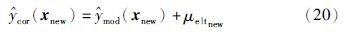
建模步骤如下所示：
(1) 收集过程的输入和输出数据组成训练数据集.
(2) 对输入和输出数据进行标准化处理，并用PCA进行信息提取得到得分矩阵.
(3) 建立得分矩阵和输出数据之间的GPR模型，然后用已经建立的GPR模型对训练数据集的得分矩阵进行预测得到预测值，最后得到输出误差.
(4) 基于输出误差和输入得分矩阵组成的误差数据集建立EGMM模型. 然后计算得到如式(16)和(17)所示的条件误差均值和方差的表达式.
(5) 对于测试集中任意一个测试数据，用PCA处理得到新的得分向量作为GPR软测量模型的输入.
(6) 计算这个新输入的预测输出值，同时用已经建立好的EGMM模型估计输出补偿μe|tnew，然后根据式(20)得到最终的输出.
为了对预测结果进行比较评价，将均方根误差(RMSE)作为性能指标，评价本文建模方法的预测能力：
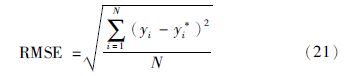
为了验证本文算法的有效性，构建一个合成数据集说明本文误差数据的特征. 这个合成数据集需要包含由多个高斯噪声叠加而成的噪声，同时具有非线性输入输出关系. 这个合成数据集的函数关系可以用如式(22)所示的数值函数描述[12]：
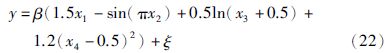
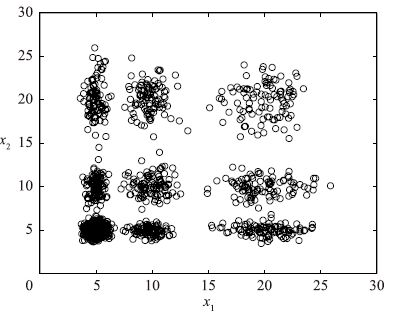
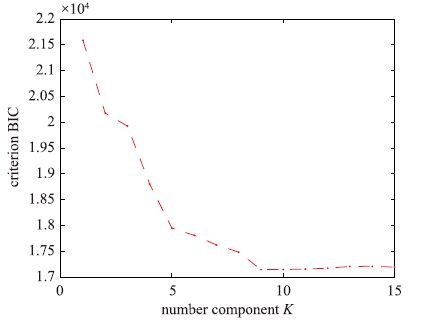
本文高斯成分协方差矩阵选择对角线形式，式(23)每一行表示相应的成分的特性. 比如，第1行表示第1个高斯分布随机向量的均值是x1=5，x2=5和ξ=0，其对角协方差矩阵是[0.25，0.25，0.062 5]I和混合系数1/9. 通过上面描述的GMM采样得到1 700个｛x1，x2，ξ｝数据，再通过对x1和x2随机重采样得到另外两个变量x3和x4. 输入向量由x1，x2，x3，x4组成，输出y由式(22)计算得到. 图 1表示合成数据的散点图，图中所示的9个高斯成分随机向量的均值分别对应于式(23)中μ0的每行的值，比如图中左下角的点集表示均值是x1=5，x2=5和ξ=0的高斯分布随机向量点的集合，右上角的点表示均值是x1=5，x2=5和ξ=0的高斯分布随机向量点的集合. x3和x4是通过对x1和x2的随机重采样得到的，因此具有与x1和x2相同的概率分布. 由于是随机重采样，x3和x4与ξ是相互独立的. 因此，误差数据可以选择为xe=[x1，x2，e]T[12]. 基于合成数据建立EGMM模型的EM算法迭代仿真结果如图 2所示. 从图中可以看出，随着高斯成分数目的增加，BIC的值不断地降低，直到高斯成分的数目K增加到9. 进一步增加K的值，BIC的值不会再降低，反而会慢慢地上升. 因此对误差数据xe=[x1，x2，e]T进行优化得到最后的高斯成分的数目K的值为9.
|
| 图 1 合成数据的散点图 Fig. 1 Scatter plots of synthetic data |
|
| 图 2 BIC值与K之间的关系 Fig. 2 The relationship between the BIC and K |
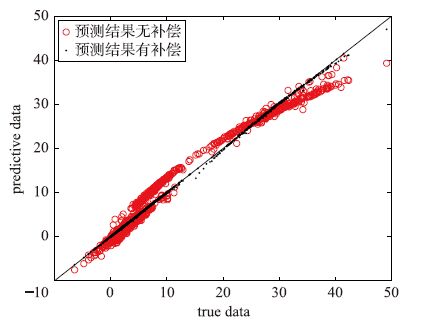
本文所提出的算法，通过建立新的EGMM模型，得到新数据的条件误差均值，对预测输出进行补偿，提高建模精度. 图 3表示对预测输出进行补偿和没有补偿时的预测结果. 可以看出，通过EGMM模型对输出进行误差信息提取，可以有效地提高预测的精度. 预测结果无补偿时RMSE为1.745 6，当对预测结果进行补偿时RMSE为0.403 6.
|
| 图 3 数值仿真预测结果 Fig. 3 Predictive results of the numerical simulation |
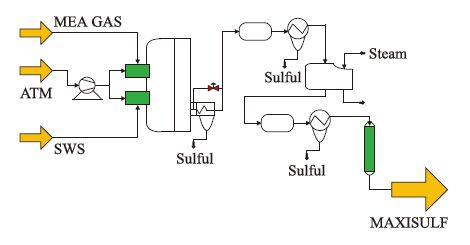
为了进一步验证本文所提方法的有效性，采用一种实际工业的数据. 硫回收装置(sulfur recovery unit，SRU)用于含硫气体(主要含有H2S，SO2)排入大气前硫的回收，以防止对环境造成污染，其装置见图 4. SRU装置主要处理两种酸性气体： 一种是富含H2S的气体(也称MEA气体)； 另一种是来自于含硫污水汽提设备(SWS)的气体，其中含有H2S、 NH3，也称为SWS气体. 主要燃烧室用于处理MEA气体，在有着充足空气(AIR_MEA)的情况下，可以充分燃烧； 另一个燃烧室用于处理SWS气体，其进入的空气流量可写为AIR_SWS. 模型的具体说明见文[21]. 5个过程变量和2个主导变量的描述见表 1所示.
|
| 图 4 硫回收装置示意图 Fig. 4 The block scheme of the SRU |
| variables | description |
| x1 | gas flow MEA_GAS |
| x2 | air flow AIR_MEA |
| x3 | secondary air flow AIR_MEA_2 |
| x4 | gas flow in SWS zone |
| x5 | air flow in SWS zone |
| y1 | concentration of H2S |
| y2 | concentration of SO2 |
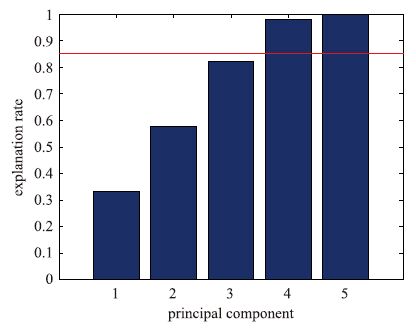
首先需要组成合适的误差数据，本文通过用PCA对输入过程变量进行主成分提取得到得分矩阵，然后基于得分矩阵和训练数据的预测误差得到误差数据. 用累计方差贡献率(cumulative percent variance，CPV)准则确定PCA模型主成分的数目，从而确保这些提取的主成分能够解释过程数据85％以上的信息. 由图 5所示，从PCA模型中提取出4个主成分. 用误差数据建立EGMM模型，其EM算法的迭代仿真结果如图 6所示.
|
| 图 5 PCA模型主成分显示解释比例 Fig. 5 Explanation rates of principal components in PCA model |
|
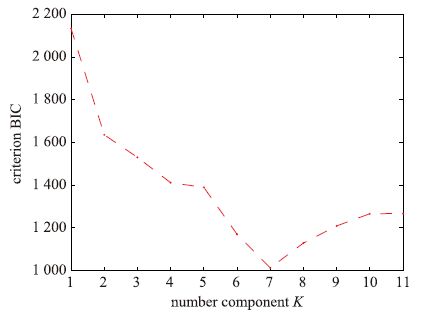
| 图 6 BIC值与K之间的关系 Fig. 6 The relationship between the BIC and K |
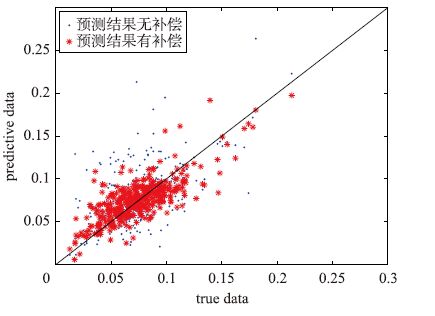
从图 6中可以看出，随着高斯成分数目的增加，BIC的值不断地降低，直到高斯成分的数目K增加到7. 此时增加或者减小K的值，BIC的值都会上升. 因此对误差数据进行优化得到最后的高斯成分的数目为7. 得到高斯成分的数目K后可以建立最合适的EGMM模型，当需要对新的输入进行输出预测时，可以通过EGMM模型提取误差信息对预测输出结果进行补偿. 如图 7所示，用EGMM进行补偿后，预测结果更加的精确，此时的RMSE为0.020 2，而没有补偿的RMSE为0.042 3. 因此本文所提出的软测量建模方法能够有效地提高预测精度.
|
| 图 7 H2S的浓度预测结果 Fig. 7 Predictive results of H2S concentration |
由于模型预测误差中常常隐含重要的信息，本文提出一种基于误差高斯混合模型的方法，对预测误差中的信息进行提取，并用于提高模型的预测精度. 通过用PCA对输入过程变量进行主成分提取，构建合适的误差数据，优化得到最优的高斯成分的数目并建立EGMM模型. 然后当到来1个新的数据时，用GPR模型对其进行输出预测，同时通过已经建立的EGMM模型求得这个新的数据的条件误差均值，用于对预测输出结果进行校正，得到更加精确的预测结果. 通过1个典型的数值仿真和实际工业过程的仿真，显示了本文方法具有更高的预测精度. 本文只研究了所建立的EGMM模型求得关于新的输入数据的条件误差均值，然而所求的条件误差方差可以对所建模的模型性能进行评估，从而判断当前模型是否需要更新，尤其对于批次工业过程，本文并没有对此进行深入的研究，将作为下一步的研究任务.
| [1] | Geladi P, Kowalski E R. Partial least-squares regression: A tutorial[J]. Analytica Chimica Acta, 1986, 185(1): 1-17. |
| [2] | Ahmed F, Nazier, S, Yeo Y K. A recursive PLS-based soft sensor for prediction of the melt index during grade change operations in HDPE plant[J]. The Korean Journal of Chemical Engineering, 2009, 26(1): 14-20. |
| [3] | Li W H, Valle-Cervantes S, Yue H H, et al. Recursive PCA for adaptive process monitoring[J]. Journal of Process Control, 2000, 10(5): 471-486. |
| [4] | Cheng C, Chiu M S. Nonlinear process monitoring using JITL-PCA[J]. Chemometrics and Intelligent Laboratory Systems, 2005, 76(1): 1-13. |
| [5] | Gonzaga J C B, Meleiro L A C, Kiang C, et al. ANN-based soft-sensor for real-time process monitoring and control of an industrial polymerization process[J]. Computers and Chemical Engineering, 2009, 33(1): 43-49. |
| [6] | 杨小梅, 刘文琦, 杨俊. 基于分阶段的LSSVM发酵过程建模[J]. 化工学报, 2013, 64(9): 3262-3269. Yang X M, Liu W Q, Yang J. LSSVM modeling for fermentation process based on dividing stages[J]. CIESC Journal, 2013, 64(9): 3262-3269. |
| [7] | 刘毅, 王海清. 采用最小二乘支持向量机的青霉素发酵过程建模研究[J]. 生物工程学报, 2006, 22(1): 144-149. Liu Y, Wang H Q. Modelling a penicillin fed-batch fermentation using least squares support vector machines[J]. Chinese Journal of Biotechnology, 2006, 22(1): 144-149. |
| [8] | Liu G H, Zhou D W, Xu H X, et al. Model optimization of SVM for a fermentation soft sensor[J]. Expert Systems with Applications, 2010, 37(4): 2708-2713. |
| [9] | Yu J. A Bayesian inference based two-stage support vector regression framework for soft sensor development in batch bioprocesses[J]. Computers & Chemical Engineering, 2012, 41(1): 134-144. |
| [10] | Rasmussen C E, Williams C K I. Gaussian processes for machine learning[M]. Cambridge, UK: The MIT Press, 2006. |
| [11] | Li X L, Su H Y, Chu J. Multiple model soft sensor based on affinity propagation, Gaussian process and Bayesian committee machine[J]. Chinese Journal of Chemical Engineering, 2009, 17(1): 95-99. |
| [12] | Yang Y Y, Mahfouf M, Panoutsos G. Probabilistic characterization of model error using Gaussian mixture model-with application to Charpy impact energy prediction for alloy steel[J]. Control Engineering Practice, 2012, 20(1): 82-92. |
| [13] | He Y, Pan W, Lin J. Cluster analysis using multivariate normal mixture models to detect differential gene expression with microarray data[J]. Computational Statistics & Data Analysis, 2006, 51(2): 641-658. |
| [14] | Huang Z K, Chau K W. A new image thresholding method based on Gaussian mixture model[J]. Applied Mathematics and Computation, 2008, 205(2): 899-907. |
| [15] | Kinnunen T, Saastamoinen J, Hautamaki V, et al. Comparative evaluation of maximum a posteriori vector quantization and Gaussian mixture models in speaker verification[J]. Pattern Recognition Letters, 2009, 30(4): 341-347. |
| [16] | Qin S J. Statistical process monitoring: Basic and beyond[J]. Journal of Chemometric, 2003, 17(8): 480-502. |
| [17] | Bishop C M. Pattern recognition and machine learning[M]. Berlin, Germany: Springer, 2006. |
| [18] | 雷瑜, 杨慧中. 基于高斯过程和贝叶斯决策的组合模型软测量[J]. 化工学报, 2013, 64(12): 4434-4438. Lei Y, Yang H Z. Combination model soft sensor based on Gaussian process and Bayesian committee machine[J]. CIESC Journal, 2013, 64(12): 4434-4438. |
| [19] | Akaike H. Information theory and an extension of the maximum-like-lihood principle//Proceedings of the 2nd International Symposium on Information Theory. Piscataway, NJ, USA: IEEE, 1973: 267-281. |
| [20] | Knoishi S, Kitagawa G. Information criteria and statistical modeling[M]. Berlin, Germany: Springer, 2007. |
| [21] | Fortuna L G, Graziani S, Rizzo A, et al. Soft sensors for monitoring and control of industrial processes[M]. Berlin, Germany: Springer-Verlag, 2007. |