2. 哈尔滨理工大学电气与电子工程学院, 黑龙江 哈尔滨 150080
1 引言
控制系统广泛应用于科学和工程应用领域. 众所周知,滤波问题在控制系统的设计及其信号处理中具有重要的理论和实际意义. 卡尔曼滤波算法[1]要求对噪声输入信号进行精确统计,且不确定性因素使其失去最优性,严重时引起滤波发散. 而H∞滤波算法[2]将噪声输入信号看作能量有界信号,有效解决了卡尔曼滤波算法对噪声输入信号的限制,同时考虑了系统参数的不确定性,具有良好的鲁棒性. 因此,H∞滤波算法受到了人们越来越多的关注.
另一方面,非线性、 时滞、 不确定性和随机因素广泛存在实际系统中,制约了系统的分析设计. 近年来,对含有这些制约因素的系统的H∞滤波问题引起了广大学者的关注,取得了相当多的研究成果. 文[3]研究了一类具有多面体不确定性系统的保H∞性能的参数依赖滤波器设计问题. 文[4]和文[5]分别针对时滞系统和非线性系统的H∞滤波器设计问题进行了研究. 文[6, 7, 8, 9]研究了一类非线性时滞系统的H∞滤波器设计问题. 文[10]考虑了时变时滞下界不为零的情形,对一类含有区间时变时滞的非线性系统的H∞滤波器设计问题进行了研究. 文[11, 12, 13, 14]研究了随机系统的H∞滤波器设计问题. 然而,上述研究结果[3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]均没有考虑随机传感器故障模型. 实际上,由于传感器部件老化,所处工作环境恶劣等原因,传感器将不可避免发生故障. 为了保证控制系统的安全性和可靠性,随机传感器故障模型在系统分析设计中也应该考虑进来[15, 16, 17]. 据作者所知,还没有满足含有随机传感器故障的非线性随机时滞系统的H∞滤波器设计问题的相应研究结果.
基于上述讨论,本文将针对一类含有随机传感器故障的随机非线性时滞控制系统的H∞滤波器设计问题进行研究. 采用时滞划分推导出滤波误差系统在概率空间上全局渐近稳定的充分条件,在此基础上得到显示表示的滤波器参数,最后通过仿真验证了设计的有效性和可靠性.
2 问题描述考虑一类含有it$\hat{o}$过程的非线性时滞系统,采用如下T-S模糊模型进行描述:
规则i: IF θ1(t)为M1i,θ2(t)为M2i,…,θg(t)为Mgi,THEN
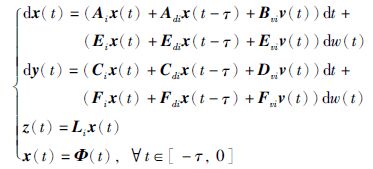
通过单点模糊化、 乘积推理、 中心平均反模糊化方法,可得下列全局动态模糊系统模型:
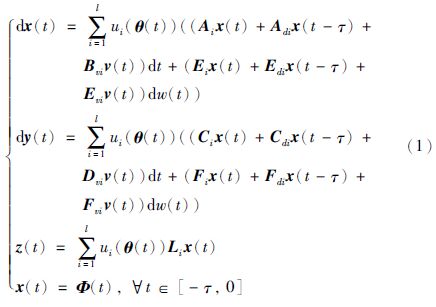
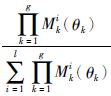 ,i=1,2,…,l,简记为ui; Mki(θk)为隶属度函数Mki作用在θk上时相应的隶属度. 任意时刻都有ui≥0,$\sum\limits_{i=1}^{l}{{}}$ui=1.
,i=1,2,…,l,简记为ui; Mki(θk)为隶属度函数Mki作用在θk上时相应的隶属度. 任意时刻都有ui≥0,$\sum\limits_{i=1}^{l}{{}}$ui=1.
通常假设滤波器和系统具有相同的模糊规则,采用类似于模糊控制器(或观测器)设计时所使用的并行分配补偿(PDC)方法. 本文设计的滤波器具有如下形式:
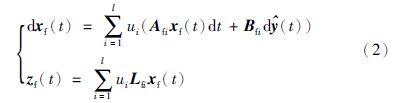
在实际的控制系统结构中,由于传感器部件老化或处于恶劣的工作环境下,因此将不可避免地发生故障. 采用如下方式建立完全或部分传感器故障模型,滤波器接收到的实际信号${\hat{y}}$(t)可描述为<

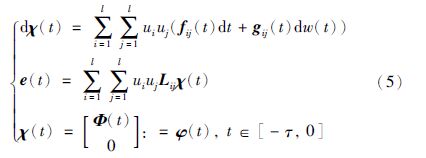
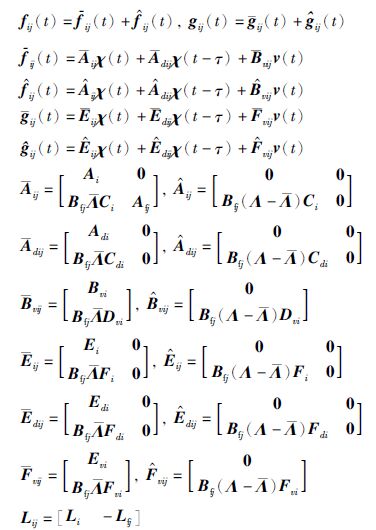
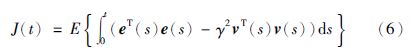
在给出本文的主要结果之前,首先引入如下的定义和引理,其对推导出本文的主要结果起到了至关重要的作用.
定义1[18] 滤波误差系统(5)如果满足下列条件:
(1) 假定存在一个正定的、 发散的及二次连续的可微的函数V(χ,t),使得
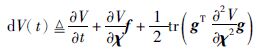
(2) 对于所有的非零干扰v(t)∈£2[0,∞),给定一个标量γ,满足:
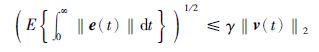
引理1[19](Schur补) 适当维数矩阵Q=QT、 R=RT、 S:
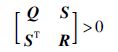
本文采用it${\hat{o}}$公式和时滞划分技术来分析设计H∞滤波器(2). 首先给出如下定理,该定理保证滤波误差系统(5)在概率空间上渐近稳定,且H∞抑制界为γ.
定理1 给定标量γ>0,τ>0和正整数λ>0,如果存在矩阵$\bar{P}$=$\bar{P}$T>0、 $\bar{Q}$=$\bar{Q}$T>0、 $\bar{S}$=$\bar{S}$T>0、 $\bar{R}$=$\bar{R}$T>0,Afj、 Bfj、 Lfj和适当维数矩阵满足下列矩阵不等式:
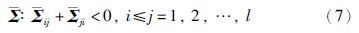

证明 将时滞区间[t-τ,t]均分为λ个子区间,并定义:
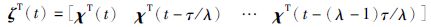
构建以下基于时滞划分的Lyapunov-Krasovskii泛函[20]:
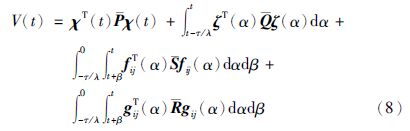
对式(8)应用it$\hat{o}$微分法则沿系统(5)的轨迹求dV(t)可得:
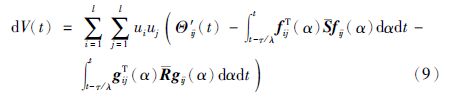
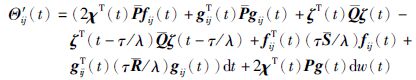
由Newton-Leibniz公式,并引进自由权矩阵${\bar{X}}$来寻找其中各项的关系,则有下式成立:
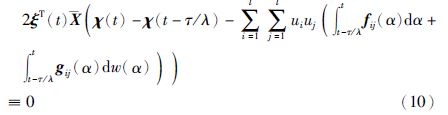
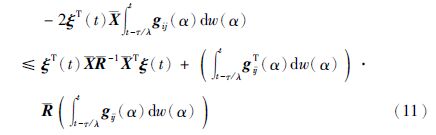
综合以上分析,联立式(9)~(11),可得
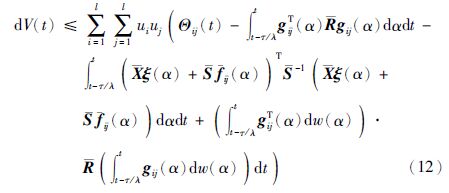
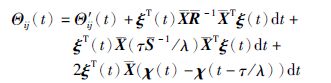
对式(12)取期望,注意到E{Λ-${\bar{\Lambda }}$}=0和由it${\hat{o}}$积分性质:
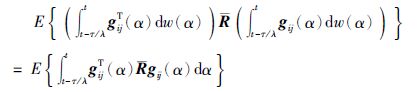
经计算可得如下结果:
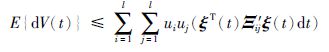
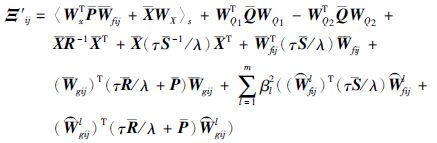
考虑加入性能指标(6),对于外界干扰v(t)∈£2[0,∞),由E{V(0)}=0,E{V(t)}≥0,根据式(6)和式(12)可得出:
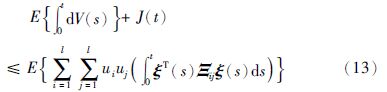
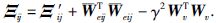 根据:
根据:
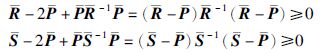
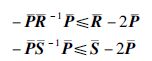
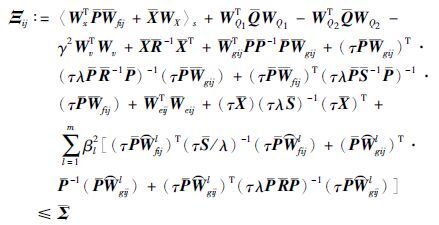
由式(7)可以看出:

第3节给出了滤波误差系统在满足一定扰动抑制能力下,系统全局渐近稳定的充分条件,但其中含有两个未知矩阵变量乘积的非线性项,且没有给出滤波器参数的显式表示. 本小节利用矩阵全等变换,对定理1进行线性化处理,同时得到当H∞性能指标γ>0给定时,滤波器相应的系数矩阵的LMI求解形式.
定理2 给定一个标量γ>0、 τ>0和一个正整数λ,如果存在矩阵P=PT>0、 Q=QT>0、 S=ST>0、 R=RT>0、 T>0、 X、 ${\tilde{A}}$fj、 ${\tilde{B}}$fj、 ${\tilde{L}}$fj满足下列LMIs:
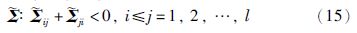


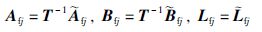
证明 将正定对称矩阵${\bar{P}}$划分为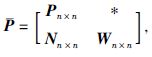 其中P=PT>0,
W=WT>0,
N=NT,令:
其中P=PT>0,
W=WT>0,
N=NT,令:
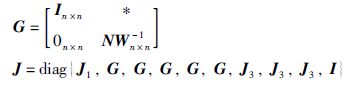
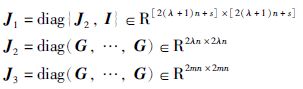
用J和JT分别左乘和右乘式(14)的两端,并引进如下新变量:
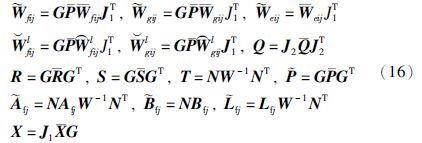
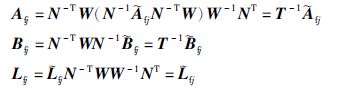
本节将给出一个数值例子,来验证本文所提出的滤波器设计方法的有效性和可靠性. 考虑基于控制系统的一个特定T-S模糊模型,其具有两个局部线性系统,参数分别为:
(1) 第1个局部线性子系统参数:
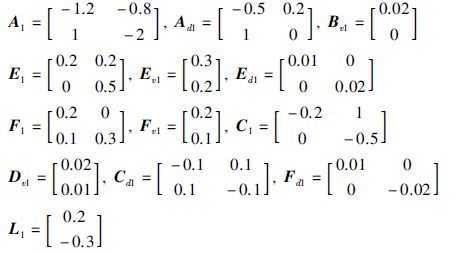
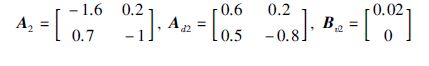
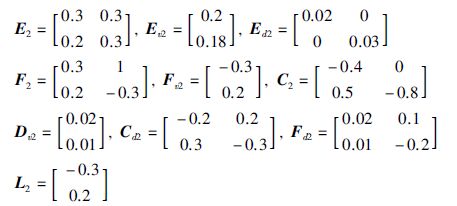
权重u1=sin2(x1(t)),u2=cos2(x1(t)); H∞抑制界γ=1.8; 时滞时间τ=0.8 s; 第1个传感器参数${\bar{\Lambda }}$1=0.8,β21=0.16; 第2个传感器参数${\bar{\Lambda }}$2=1.1,β22=0.09. 此时对应的传感器参数${\bar{\Lambda }}$=diag(${\bar{\Lambda }}$1,${\bar{\Lambda }}$2)=$\left[ \begin{matrix} 0.8 & 0 \\ 0 & 1.1 \\ \end{matrix} \right]$,β=$\left[ \begin{matrix} 0.4 & 0 \\ 0 & 0.3 \\ \end{matrix} \right]$. 根据给定参数下滤波误差系统是否有可行解选择合适的时滞划分数λ. 这里取λ=1就可以使时滞系统具有可行解,应用定理2可以求解出需要设计的滤波器参数为

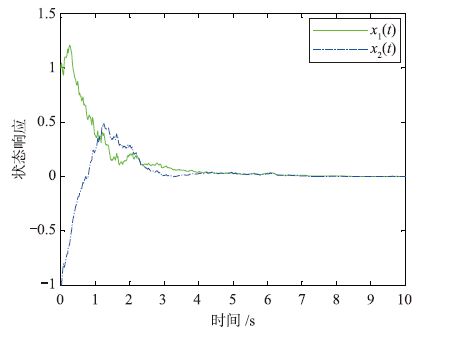
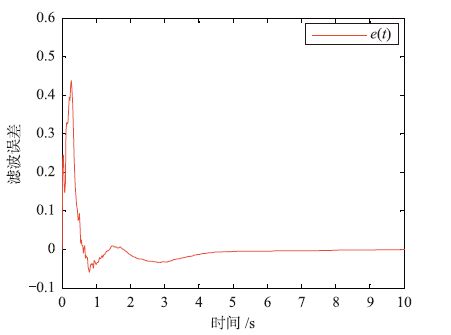
选择外部输入干扰为v(t)=$\frac{{{e}^{-t}}}{1+t}$,t≥0,系统初始状态χ(t)=[1, -1, 0, 0]T,仿真时间T=10 s,仿真步数为210,仿真结果如图 1、 2所示.
|
| 图 1 状态响应 Fig. 1 State response |
|
| 图 2 滤波误差 Fig. 2 Error of filtering |
从图 1可以看出,含有随机传感器故障和随机摄动的系统状态响应能很快收敛到初始状态,并一直保持稳定. 从图 2可以看出,滤波误差很快趋于0,滤波器的估计输出跟踪系统的估计输出.
根据以上仿真结果可以看出,含有随机传感器故障和随机摄动的系统在外界干扰作用下能够保持稳定,系统具有很好的安全性和鲁棒性. 因此,所设计的滤波器能够满足系统滤波需要.
6 结论本文研究了一类含有随机传感器故障和it${\hat{o}}$过程的非线性时滞控制系统的H∞滤波器设计问题. 主要应用it公式,时滞划分技术和LMI方法来分析和设计滤波器. 所设计的滤波器能够满足一类同时具有随机传感器故障和随机摄动的非线性时滞控制系统的滤波需要,且满足H∞范数界. 仿真结果表明了设计方法的有效性和可靠性.
本文的研究结果是基于传统控制系统框架下被控对象的数学模型为具有定常时滞的非线性随机系统. 一方面,定常时滞为时变时滞的特殊情况; 另一方面,网络控制系统广泛应用在汽车工业,远程操控,飞行器系统等领域,带来了许多革新性的影响. 因此,考虑基于网络的具有随机传感器故障的非线性随机时变时滞系统的H∞滤波器设计问题,有待今后进一步深入研究.
| [1] | Kalman R E. A new approach to linear filtering and prediction problem[J]. Journal of Basic Engineering, 1960, 82(1): 35-45. |
| [2] | Elsayed A, Grimble M J. A new approach to the H∞design of optimal digital linear filters[J]. IMA Journal of Mathematical Control and Information, 1989, 6(2): 233-251. |
| [3] | Gao H J, Lam J, Shi P, et al. Parameter-dependent filter design with guaranteed H∞ performance[J]. IEE Proceedings-Control Theory and Applications, 2005, 152(5): 531-537. |
| [4] | 扶凌云, 何勇, 吴敏. 基于时滞的H∞滤波器设计及其在网络中的应用[J]. 控制理论与应用, 2010, 27(4): 517-522. Fu L Y, He Y, Wu M. H∞ filter design based on time-delay and its application to network[J]. Control Theory and Applications, 2010, 27(4): 517-522. |
| [5] | Coutinho D F, Souza C E D, Barbosa K A, et al. Robust linear H∞ filter design for a class of uncertain nonlinear systems: An LMI approach[J]. Siam Journalon Control and Optimization, 2009, 48(3): 1452-1472. |
| [6] | Yang R Y, Shi P, Liu G P. Filtering for discrete-time networked nonlinear systems with mixed random delays and packet dropouts[J]. IEEE Transactions on Automatic Control, 2011, 56(11): 2655-2660. |
| [7] | Shao H Y. Robust H∞ filtering for class of non-linear discrete time-delay systems with parameter uncertainties[J]. Control Theory and Applications, 2007, 24(1): 148-154. |
| [8] | Huang S J, He X Q, Zhang N N. New results on H∞ filter design for non-linear systems with time-delay via T-S fuzzy models[J]. IEEE Transactions on Fuzzy Systems, 2011, 19(1): 193-199. |
| [9] | Mad Z, Zhang H G, Wang Z S, et al. The robust H∞ filter design for a class of non-linear time-delay systems[J]. Acta Electronica Sinica, 2010, 38(9): 2172-2178. |
| [10] | Deng Z, Shi P, Yang H, et al. Robust H∞ filtering for non-linear systems with interval time-varying delays[J]. International Journal of Innovative Computing Information and Control, 2010, 6(12): 5527-5538. |
| [11] | Gao H J, Lam J, Wang C H. Robust energy-to-peak filter design for stochastic time-delay systems[J]. Systems and Control Letters, 2006, 55(2): 101-111. |
| [12] | Yan H C, Zhang H, Shi H B, et al. Robust H∞ filtering for uncertain non-linear stochastic systems with mode-dependent time-delays and Markovian jump parameters[J]. Circuits Systems and Signal Processing, 2011, 30(2): 303-321. |
| [13] | Zhao F, Zhang Q L, Liu C, et al. H∞ filtering for a class of stochastic time-delay non-linear systems[C]//Control and Decision Conference. Piscataway, NJ, USA: IEEE, 2014: 3119-3124. |
| [14] | Tseng C S. Robust fuzzy filter design for a class of non-linear stochastic systems[J]. IEEE Transactions on Fuzzy Systems, 2007, 15(2): 261-274. |
| [15] | Tian E G, Yue D. Reliable H∞ filter design for T-S fuzzy model based networked control systems with random sensor failure[J]. International Journal of Robust and Non-linear Control, 2013, 23(1): 15-32. |
| [16] | Chen B, Yu L, Zhang W A, et al. Robust information fusion estimator for multiple delay-tolerant sensors with different failure rates[J]. IEEE Transaction on Circuits and Systems, 2013, 60(2): 401-414. |
| [17] | Wang X, Yaz E E, Jeong C S, et al. A resilient extended Kalman filter for discrete-time nonlinear stochastic systems with sensor failures[C]//American Control Conference (ACC). Piscataway, NJ, USA: IEEE, 2012: 4783-4788. |
| [18] | 吴立刚, 王常虹, 高会军, 等. 时滞不确定随机系统基于参数依赖Lyapunov函数的稳定性条件[J]. 控制理论与应用, 2006, 10(1): 607-612. Wu L G, Wang C H, Gao H J, et al. Stability of uncertain stochastic systems with time-varying delays based on parameter-dependent Lyapunov functional[J]. Control Theory and Applications, 2006, 10(1): 607-612. |
| [19] | Boyd S P, Ghaoui L E, Feron E, et al. Linear matrix inequalities in systems and control theory[J]. Proceedings of Symposia in Pure Mathematics, 1994, 85(5): 798-799. |
| [20] | Yang R N, Gao H J, Shi P. Delay-dependent robust H∞ control for uncertain stochastic time-delay systems[J]. International Journal of Robust and Nonlinear Control, 2010, 20(16): 1852-1865. |
| [21] | Lin C, Wang Q G, Lee T H, et al. H∞ filter design for non-linear systems with time-delay through T-S fuzzy model approach[J]. IEEE Transactions on Fuzzy Systems, 2008, 16(3): 739-746. |



