2. 中国民航大学航空自动化学院, 天津 300300;
3. 中国民航局第二研究所, 四川 成都 610041
3. The Second Research Institute of Civil Aviation Administration of China, Chengdu 610041, China
1 引言
目前，国内外多数枢纽机场由于跑道、 滑行道和停机位等资源的限制，机场道面拥挤、 通行能力下降、 转场效率降低[1, 2, 3]. 为此，旨在最大化滑行道资源利用率的飞机地面滑行路径优化已成为民航领域的热点研究问题[4, 5, 6, 7, 8]. 飞机地面滑行路径优化有进港和离港之分[9, 10]. 本文主要研究离港航班的滑行优化，研究的核心是如何分配飞机从停机位推出之后，到达跑道口之前的滑行路径.
现有的离港航班滑行路径优化算法[11, 12, 13, 14]的目标在于最小化滑行距离或滑行时间. 然而，在实际应用中，航空公司满意度和滑行道负载率才是离港航班滑行优化最核心的因素. 其中航空公司满意度建立在飞机滑行时间之上，其直观含义是： 与理论滑行时间相比，飞机实际滑行时间越小，航空公司满意度越高. 滑行道负载率则是评价滑行道密度的指标. 为此，本文首次提出基于背压路由算法的离港滑行路径优化算法. 本文的主要贡献包括：
(1) 指出离港航班滑行路径优化的核心关注点——航空公司满意度和滑行道负载率，进而为离港航班滑行路径优化指出新的研究方向.
(2) 将机场结构简化为有向网络拓扑结构，进而将离港滑行路径优化问题等价转化为网络拓扑结构中路由搜索问题，为飞机地面滑行路径优化问题提供新的研究思路.
2 飞机地面滑行模型假设国内某大型枢纽机场某天有R架离港航班，离港航班地面滑行路径优化模型的优化目标是针对每一架离港航班，构建一条从滑行起点到跑道端口起飞等待点的滑行路径. 在本文中，除了保障每一架离港航班在滑行过程中不会出现冲突，还应该最大化航空公司满意度和最小化滑行道负载率.
2.1 航空公司满意度记航班i从源节点s到目标节点d的期望滑行时间为a，航空公司可以承受的最长滑行时间为b，即时间窗宽度为b-a，则航空公司满意度函数定义为
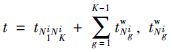为航班i滑行过程中的等待时间. 当机场航班量较小时，滑行过程中没有停止等待，飞机i的无拥挤滑行时间表示为<
当机场处于繁忙时期，航班量较大时，会有航班等待. 若前后两航班属性相同则采取先到先服务[15]的原则，则有：
若采用优先级队列[8]，则有：
滑行道负载可由在滑行道上滑行的飞机数表示，某一滑行链接上经过的飞机数越多，表示该链接负荷越重. 定义所有链接的密度函数为滑行道负载[16]：
滑行道密度ρg是与链接平均速度相关的变量，当系统中滑行飞机数量较多时，飞机在滑行道的速度减小. 用ρupperg表示链接g允许的最大密度，gi表示飞机i在链接g的平均滑行速度，Umax为飞机最大滑行速度，则有：
结合以上表述，飞机i从源节点s滑行至目标节点d的优化目标为
背压路由算法[17]起源于Tassiulas和Ephremides提出的无线数据包多跳网络[18, 19, 20, 21]. 其最早被用于通信网络，而后在无线传感器、 产品装配及处理网络等领域得到广泛应用[22, 23]. 随着资源调度优化问题日益突出，将背压路由算法引入有限资源的分配，已经成为颇为前沿的研究方法[24]，如何基于背压路由算法对飞机地面滑行路径进行优化是本文研究的主要问题.
3.1 算法描述基于背压路由的离港航班滑行路径优化算法的核心思想是： 路径选择概率是链接空闲容量和航班到目的地紧急程度的权值和，即在所有候选路径集合中，航班选择某一滑行链接的概率与该链接可接受的滑行飞机数目与飞机滑行时间密切相关.
3.2 算法流程利用上述所建模型，依据飞机地面运行流程对机场场面运行状态进行模拟. 获得航空器在机场地面的运行状态之后，即可进行运算. 算法的输入为与节点Ng相邻的每个滑行链接上的飞机数、 飞机i的候选路径、 i的期望到达时间及当前滑行时间. 输出为proi，g，表示离开节点Ng的飞机i对下一个节点Ng+1的选择概率.
(1) 获取与滑行道交叉点Ng相邻的节点集合N(i). 即对于某一滑行道交叉点，找出所有与该点相连接的滑行道以及其所对应的交叉点.
(2) 对任意与节点Ng相邻的点Ng+1∈N(i)，计算链接(Ng-1，Ng)和链接(Ng，Ng+1)之间的压力差值，记为bpi，g. 即计算当前滑行道和候选的下一滑行道上(含节点处等待的)飞机数目的差值.
(3) 算出选择与当前滑行道相邻的其它链接背压概率：
(4) 与航空公司满意度相对应，此处计算航班i滑行至跑道端口起飞等待点的紧急程度，用Urg表示：
(5) 如果飞机预选择的下一滑行道交叉点Ng+1在航空器i候选的最短路径上，那么该算法选择滑行链接(Ng，Ng+1)作为下一目标路径的概率可表示为
如果飞机预选择的下一滑行道交叉点Ng+1不在其候选的最短路径上，则算法选择滑行链接(Ng，Ng+1)的概率表示为
该步骤的意义在于： 若航空器所对应的紧急程度较高，则其选择最短路径的概率较大，否则偏小.
4 算例分析 4.1 算例描述图 1为国内某大型枢纽机场部分网络拓扑图，各节点编号如图所示. 此处仅考虑离港飞机从停机位推出后的滑行过程. 在图 2中，离港飞机滑行起点集合S=｛1，4，9，3，6，11，12，13，14，15，21，22，23｝，代表与停机位相连的滑行节点； 滑行终点则是与跑道端口飞机起飞等待队列相连的节点D=｛39，40｝； 离港航班滑行的中间节点集合O=｛2，5，7，8，10，16，17，18，19，20，24，25，26，27，28，29，30，31，32，33，34，35，36，37，38｝，其含义为各滑行道的交叉点. 进而飞机的滑行路径可由一系列节点的组合表示，如从停机位推出后进入9号节点的航班，其滑行路径可描述为M=｛9，17，34，35，36，37，39｝.
|
| 图 1 国内某大型枢纽机场部分网络拓扑图 Fig. 1 Part of the network topology of a domestic hub airport |
|
| 图 2 从停机位推出后进入9号节点的航班的滑行时间 Fig. 2 Taxiing time of flights between the pushing-back from gates and the entering of node 9 |
通过分析国内某大型枢纽机场2013年8月至2014年3月八个月的航班实际运行数据，利用上述数学模型，对机场运行状态进行建模，从航班正点情况、 机场通行量、 飞机滑行时间、 航空公司满意度和滑行道负载等方面进行研究.
机场的航班到达服从一定参数的泊松过程. 利用蒙特卡洛算法原理，依据实际航班运行数据，截取各停机位一天内7∶ 00—23∶ 00的航班推出时间及预计到达时间来模拟整个机场地面的航班运行，并对拥挤状态下飞机地面运行进行仿真.
由于从各停机位推出的航班运行趋势大同小异，故以从停机位推出后进入9号滑行节点滑行的航班为例，利用最短路径算法获得的飞机实际开机滑行时间、 运用背压路由算法得到的飞机地面开机滑行时间以及期望滑行时间如图 2所示. 结果表明，当机场表面滑行飞机较少，处于空闲状态时，最短路径算法获得的路径具有最少的滑行时间； 随着地面飞机数增多，本文所提算法可以有效地避免拥挤，为航班选择一条最优路径，极大地减小了飞机地面总滑行时间，使其尽快到达跑道等待队列等待起飞.
飞机滑行过程中的停止等待是造成航班延误的很重要的一个因素，故利用背压路由算法为航班重新规划滑行路径具有重要意义.
最短路径算法获得的各个链接的滑行道效用分配不均，而BPR-AS可以在保证机场容量的条件下，有效地平滑除了跑道端口及停机位连接处，飞机必经滑行链接之外的滑行道密度，平均滑行道负载，使系统获得较好的滑行道效用. 优化前后航空公司满意度及滑行道负载情况分别如图 3、 4所示. 结果表明，所提算法在保障航空公司满意度的同时，减小了滑行道负载. 滑行道平均负载率从原先的0.34减小到0.25，大大地提高了机场运行效率.
|
| 图 3 航空公司对从停机位推出后到达9号节点的航班的满意度 Fig. 3 The airline satisfaction for flights that enter node 9 after pushed-back from gates |
|
| 图 4 各滑行链接的滑行道负载情况 Fig. 4 The taxiway load of each taxiing link |
背压路由算法有效地避免了滑行过程中的航班冲突，利用该算法为航班分配的滑行路径大大地减少了飞机滑行过程中的停止等待，降低了飞机开机滑行时间，从而提高了机场场面运行效率，使航班正点率得到提升. 同时该算法能够自动依据机场场面运行状况，为航班选择滑行路径，有效地避开了拥挤，使得部分使用频率较低的滑行道得到合理利用，平均滑行道负载，很大程度上提高了滑行道系统的利用率.
5 结论首次定义了“航空公司满意度—滑行道负载”问题，并将背压路由算法应用于飞机滑行路径选择，提出了新的算法来解决上述问题. 根据从机场获得的实际数据进行仿真，证明了该算法在满足航空公司满意度和平均道路密度方面的有效性. 需要指出的是，本文提出的算法除了针对单一航班进行分析，为离港飞机选择最优的滑行路径之外，其它诸如机场通行量优化、 多航班冲突避免等也在研究范围之内，然而系统稳定性方面的问题则在后续工作中考虑.
| [1] | Anderson R, Milutinovic D. An approach to optimization of airport taxiway scheduling and traversal under uncertainty[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2013, 227(2): 273-284. |
| [2] | Ball M O, Hoffman R, Odoni A, et al. A stochastic integer program with dual network structure and its application to the ground-holding problem[J]. Operations Research, 2003, 51(1): 167-171. |
| [3] | Odoni A R, Bianco L, Szego G, et al. The flow management problem in air traffic control in flow control of congested networks[M]//Flow Control of Congested Networks: NATO ASI Series, Vol.38. Berlin, Germany: Springer-Verlag, 1987: 269-288. |
| [4] | Khadilkar H. Analysis and modeling of airport surface operations[D]. Cambridge, MA, USA: Massachusetts Institute of Technology, 2011. |
| [5] | Jiang Y, Liao Z H, Zhang H H. A collaborative optimization model for ground taxi based on aircraft priority[J]. Mathematical Problems in Engineering, 2013, 2013: ID 854364. |
| [6] | Khadilkar H, Balakrishnan H. Control of aircraft pushbacks at an airport using a dynamic programming formulation[C]//AIAA Guidance, Navigation, and Control Conference. Los Angeles, CA, USA: AIAA, 2012: AIAA 2012-5022. |
| [7] | Simaiakis I, Khadilkar H, Balakrishnan H, et al. Demonstration of reduced airport congestion through pushback rate control[J]. Transportation Research Part A: Policy and Practice, 2014, 66: 251-267. |
| [8] | 邢志伟, 唐广群, 任准. 多除冰坪排队飞机除冰过程调度非合作博弈[J]. 信息与控制, 2013, 42(4): 511-515. Xing Z W, Tang G Q, Ren Z. Queuing aircraft deicing-dispatch in multi-deicing bays based on non-cooperative game theory[J]. Information and Control, 2013, 42(4): 511-515. |
| [9] | Simaiakis I, Sandberg M, Balakrishnan H, et al. Design, testing and evaluation of a pushback rate control strategy[C]//International Conference on Research in Air Transportation. 2012. |
| [10] | Khadilkar H, Balakrishnan H. Optimal control of airport operations with gate capacity constraints[EB/OL]. [2013-05-01]. http://web.mit.edu. |
| [11] | Zhang R, Li Z, Feng C, et al. Traffic routing guidance algorithm based on backpressure with a trade-off between user satisfaction and traffic load[C]//2012 Vehicular Technology Conference (VTC Fall). Piscataway, NJ, USA: IEEE, 2012: 1-5. |
| [12] | Bertsimas D, Gupta S. A proposal for network air traffic flow management incorporating fairness and airline collaboration[EB/OL]. [2011-04-25]. http://web.mit.edu. |
| [13] | Balakrishnan H, Jung Y. A framework for coordinated surface operations planning at Dallas-Fort Worth International Airport[C]//AIAA Guidance, Navigation, and Control Conference. Los Angeles, CA, USA: AIAA, 2007: 2382-2400. |
| [14] | Liu C, Guo K. Airport taxi scheduling optimization based on genetic algorithm[C]//2010 International Conference on Computational Intelligence and Security (CIS). Piscataway, NJ, USA: IEEE, 2010: 205-208. |
| [15] | Mou D Y, Liu J F. An improved ant colony algorithm for aircraft routing[J]. Computer Engineering and Science. 2012, 34(6): 136-139. |
| [16] | Clare G L, Richards A G. Optimization of taxiway routing and runway scheduling[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(4): 1000-1013. |
| [17] | Barnhart C, Bertsimas D, Caramanis C, et al. Equitable and efficient coordination in traffic flow management[J]. Transportation Science, 2012, 46(2): 262-280. |
| [18] | Sridharan A, Moeller S, Krishnamachari B. Making distributed rate control using Lyapunov drifts a reality in wireless sensor networks[C]//6th International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks and Workshops. Piscataway, NJ, USA: IEEE, 2008: 452-461. |
| [19] | Smeltink J W, Soomer M J, Waal P R, et al. An optimisation model for airport taxi scheduling[C]//Proceedings of the INFORMS Annual Meeting. 2004. |
| [20] | Szwabe A, Misiorek P, Nowak A, et al. Implementation of backpressure-based routing integrated with max-weight scheduling in a wireless multi-hop network[C]//35th IEEE Conference on Local Computer Networks (LCN). Piscataway, NJ, USA: IEEE, 2010: 983-988. |
| [21] | Laufer R, Salonidis T, Lundgren H, et al. A cross-layer backpressure architecture for wireless multihop networks[J]. IEEE/ACM Transactions on Networking, 2014, 22(2): 363-376. |
| [22] | Moeller S, Sridharan A, Krishnamachari B, et al. Backpressure routing made practical[C]//IEEE Conference on Computer Communications Workshops. Piscataway, NJ, USA: IEEE, 2010: 1-2. |
| [23] | Seferoglu H, Modiano E. Diff-Max: Separation of routing and scheduling in backpressure-based wireless networks[J]. Proceedings-IEEE INFOCOM, 2012, 12(11): 1555-1563. |
| [24] | Nunez-Martínez J, Mangues-Bafalluy J. Distributed Lyapunov drift-plus-penalty routing for Wifi mesh networks with adaptive penalty weight[C]//2012 IEEE International Symposium on World of Wireless, Mobile and Multimedia Networks (WoWMoM). Piscataway, NJ, USA: IEEE, 2012: 1-6. |
| [25] | Feng H, Molisch A F. Diversity backpressure routing with mutual information accumulation in wireless ad-hoc networks[C]//2012 IEEE International Conference on Communications (ICC). Piscataway, NJ, USA: IEEE, 2012: 4055-4060. |