1 引言
自从Pecora和Carroll开创性地提出并在电子电路上实现了两个相同混沌系统的驱动—响应同步[1]以来,混沌同步由于其自身的理论价值及其在信息处理、 保密通信、 生物工程和化学加工等领域的应用前景而受到了学者们的广泛关注. 随着现代高速计算机、 微电子、 通信网络的迅猛发展,数字控制器逐渐取代了模拟电路来控制和同步连续时间混沌系统. 一些学者提出了各种有效实现混沌控制的方法并拓宽了混沌同步的概念[2],如混沌Lur′e系统基于时滞反馈控制的完全同步[3],混沌神经网络基于分散控制的驱动—响应同步[4]和基于采样数据反馈控制的指数同步[5],四维混沌系统基于自适应控制的改进投影同步[6],超混沌系统基于自适应控制和主动控制的改进投影同步[7],混沌系统基于可靠反馈控制的完全同步[8]、 基于主动滑模控制的改进投影同步[9]和改进函数投影滞后同步[10]、 基于改进主动滑模控制的完全同步[11]及信息约束下的耗散同步[12]等.
Lur′e系统是一类典型的非线性系统,其非线性项通常满足一个扇形有界的约束条件. 许多实际控制系统如Chua电路和n-涡卷超混沌吸引子等都可以表述成Lur′e系统的形式[13, 14],混沌Lur′e系统的同步问题一直备受学术界和工程界的关注,研究人员提出并实现了混沌Lur′e系统的完全同步[3],混沌Lur′e系统的采样数据同步[15, 16, 17, 18],时滞混沌Lur′e系统的指数同步[19, 20]. 文[3]利用常时滞输出反馈控制器给出了两个相同的混沌Lur′e系统的完全同步,但文中使用一个积分不等式来放缩Lyapunov-Krasovskii泛函(Lyapunov-Krasovskii functional,LKF)导数的交叉项上界可能会带来一些保守性. 文[15]应用线性矩阵不等式技术和自由权矩阵方法给出了两个相同的混沌Lur′e系统基于采样数据控制器的全局渐近同步的一个充分条件,但由于忽略了系统的一些有用的信息(如所构造的LKF中没有考虑扇形有界的约束条件),文中所得到的结果存在保守性. 文[16]通过定义一个增广的LKF泛函及利用自由权矩阵方法改进了文[15]中的同步判据,但文中忽略了时滞在采样时刻不连续的特性而使得文中的LKF可能只适用于某些情形. 为降低保守性,文[17]构造了一个分段LKF并利用凸组合方法给出了文[15, 16]中Lur′e系统的全局渐近同步的一个判据,但文中LKF导数中积分项的处理需要另外的放大(见文[17]中的式(17)和式(18)),这可能也会带来一些保守性. 文[18]应用自由权矩阵技术构造的LKF确保了LKF在采样时刻的非增,改进了文[17]中的同步判据,但也忽略了非线性函数的一些有用的信息. 文[19]研究了带有采样数据控制器的常时滞混沌Lur′e系统的指数同步,应用Jensen不等式技术来放缩LKF导数的交叉项上界. 文[20]利用时变时滞静态输出脉冲反馈控制器给出了两个相同的混沌Lur′e系统的全局指数同步,但文中非线性函数所满足的Lipschitz条件只是扇形条件的一个特殊情形. 应该指出的是,文[3, 15, 16, 17, 18]中所研究的系统均为不含时滞的混沌Lur′e系统; 文[19]所研究的系统为带有常时滞的混沌Lur′e系统; 文[20]所涉及的系统虽为带有时变时滞的混沌Lur′e系统,但其非线性函数所满足的条件不具有一般性. 据作者所知,有关非线性函数满足一般扇形条件的带有时变时滞的混沌Lur′e系统的同步结果还鲜有报道,这个问题值得研究且具有挑战性.
受前述文献的启发,本文研究带有时变时滞的混沌Lur′e系统的采样数据指数同步问题,所考虑的非线性函数满足更具一般性的扇形条件并在构造LKF时考虑了这个条件. 我们先根据输入时滞法[21]将采用数据误差系统转化为带有两个时变时滞的连续系统,然后基于Lyapunov-Krasovskii稳定性理论、 自由权矩阵方法及线性矩阵不等式技术,提出了一种新的时滞相关指数同步判据并设计了相应的采样数据控制器,实现了带有时变时滞的混沌Lur′e系统的采样数据指数同步并通过时滞Chua电路的数值仿真验证了本文所提出控制方法的有效性.
本文采用以下记号: Rn表示n维Euclid空间; Rn×m表示n×m实矩阵集合; P>0(≥0)表示P为实对称正定(半正定)矩阵; I和0分别表示适当维数的单位矩阵和零矩阵; diag(·)表示分块对角矩阵; λmax(P)和λmin(P)分别表示矩阵P的最大和最小特征值; 对称矩阵中的对称项用*表示.
2 问题描述考虑如下的两个时滞混沌Lur′e系统
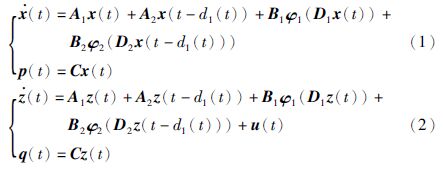
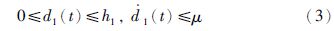
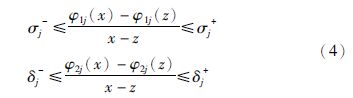
注1 值得注意的是扇形条件(4)比文[3],[16],[19],[22]和[23]中所用的同样条件更具有一般性. 其主要区别在于条件(4)中所引入的下界σj-和δj-,如果假设σj-=0且δj-=0,则条件(4)就退化为文[3],[16],[19],[22]和[23]中所用的扇形条件了.
注2 常数σj+,σj-和δj+,δj-可以是正数、 负数或零. 因而通常所用的Lipschitz条件(例如文[4])只是条件(4)的一个特殊情形.
定义同步误差e(t)=x(t)-z(t),则由驱动系统(1)和响应系统(2)可得误差系统为
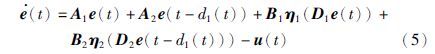
由式(4)可得ηij(·)满足以下条件
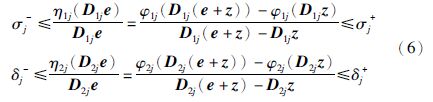
考虑如下形式的采样数据控制器
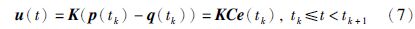
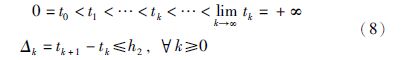
将式(7)带入式(5)得
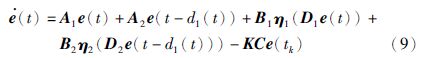
由于存在离散项e(tk),所以不便于分析误差系统(9)的同步问题. 为此,根据输入时滞法[21],可将tk定义为
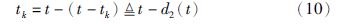
将式(10)带入式(9)得
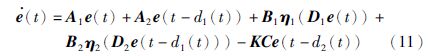
注3 如果A2=0,B2=0,d2(t)=τ(常数),则系统(11)退化为文[3]中的误差系统.
定义1 (指数同步[5, 19, 20, 25])驱动系统(1)和响应系统(2)称为是指数同步的,如果存在标量k>0和β≥1使得
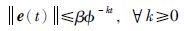
本文所研究的问题可以表述为: 设计采样数据控制器u(t),使得误差系统(5)的状态在任意e(0)≠0的条件下以指数率收敛于0,从而实现驱动系统(1)和响应系统(2)在任意不同的初始条件下的指数同步.
在导出新的判据时要用到下列引理.
引理1[22, 23] 对于任意给定适当维数的向量a、 b和正定矩阵X,下列不等式成立
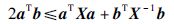
下面的引理2是文[22]中引理2和文[23]中引理4的一个推广.
引理2 如果式(6)成立,则对于j=1,2,…,m,有
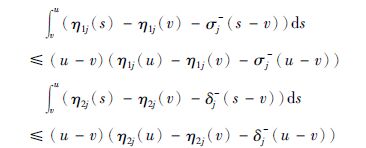
证 定义连续函数
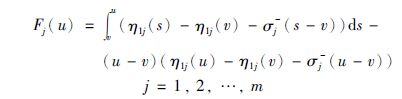
则Fj(u)的上右导数[24]为

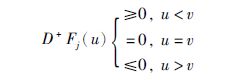
这说明u=v是函数Fj(u)的最大值点,因而对任意u∈R都有Fj(u)≤Fj(v)=0,即第1个不等式成立.
第2个不等式类似可证.
为了表示方便,记
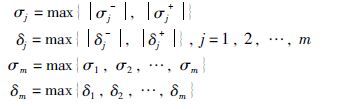
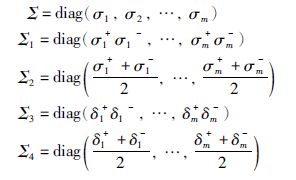
本节通过引入自由权矩阵来表示系统变量和Newton-Leibniz公式中各项之间的关系来给出驱动系统(1)和响应系统(2)的指数同步判据,并给出确保混沌Lur′e系统指数同步的采样数据控制器设计方法.
定理1 考虑带有时变时滞d1(t)的驱动系统(1)和响应系统(2),d1(t)满足式(3). 对于给定的标量hi>0(i=1,2),k>0,μ<1,如果存在矩阵$P ≥ 0,Q = \left[ {\begin{array}{*{20}{c}} {{Q_{11}}}&{{Q_{12}}} \\ *&{{Q_{22}}} \end{array}} \right] ≥ 0,{R_i} ≥ 0,{Z_i} ≥ 0,{X^{\left( i \right)}} = \left[ {\begin{array}{*{20}{c}} {X_{11}^{\left( i \right)}}&{X_{12}^{\left( i \right)}} \\ *&{X_{22}^{\left( i \right)}} \end{array}} \right] ≥ 0$(i=1,2), 对角矩阵L≥0,U>0,V>0和W>0以及任意适当维数的矩阵G1,G2,M(i)=[Mi1T Mi2T]T及N(i)=[Ni1T Ni2T]T(i=1,2),使得下列线性矩阵不等式是可行的
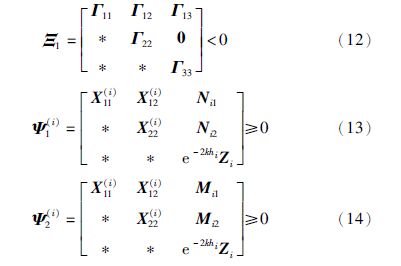

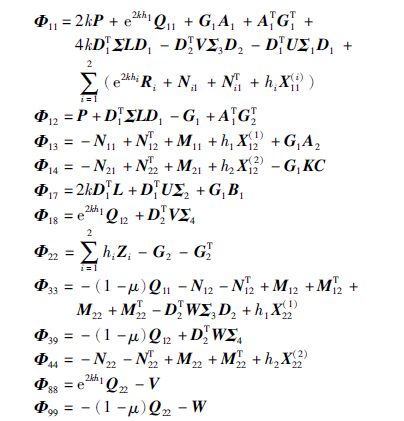
证 选取如下的Lyapunov-Krasovskii泛函
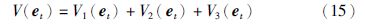
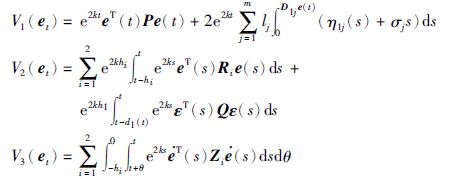
这里P≥0,$Q = \left[ {\begin{array}{*{20}{c}} {{Q_{11}}}&{{Q_{12}}} \\ *&{{Q_{22}}} \end{array}} \right] ≥ 0,{R_i} ≥ 0,{Z_i} ≥ 0$(i=1,2),L=diag{l1,l2,…,lm}≥0,ε(t)=[eT(t),η2T(D2e(t))]T,则Vi(et)(i=1,2,3)对时间t的导数为
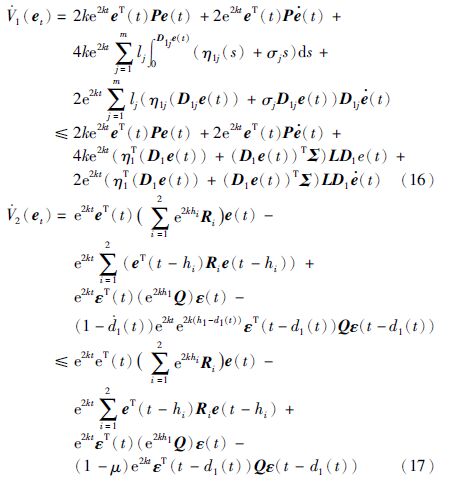
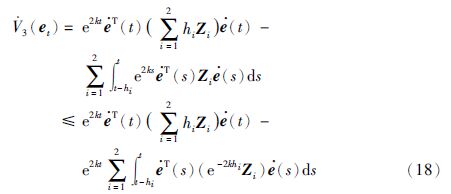
对任意适当维数的矩阵${M^{\left( i \right)}} = \left[ {\begin{array}{*{20}{c}} {{M_{i1}}} \\ {{M_{i2}}} \end{array}} \right]$和${N^{\left( i \right)}} = \left[ {\begin{array}{*{20}{c}} {{N_{i1}}} \\ {{N_{i2}}} \end{array}} \right]$(i=1,2),由Newton-Leibniz公式可知下列等式成立
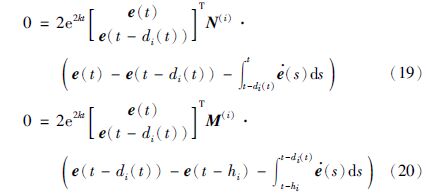
对任意适当维数的矩阵G1和G2,由误差系统(11)可得
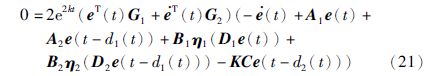
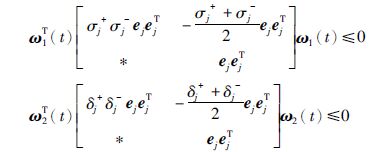
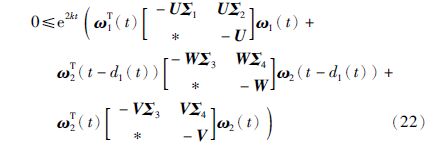
此外,对任意半正定矩阵${X^{\left( i \right)}} = \left[ {\begin{array}{*{20}{c}} {X_{11}^{\left( i \right)}}&{X_{12}^{\left( i \right)}} \\ *&{X_{22}^{\left( i \right)}} \end{array}} \right] ≥ 0$和ξi(t)=[eT(t),eT(t-di(t))]T,i=1,2,以下等式成立
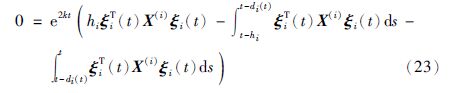
将式(16)~式(23)的右半部分加到${\dot V}$(et)得

其中,Ξ1、 Ψ1(i)和Ψ2(i)分别如式(12)、 (13)和(14)所定义,且
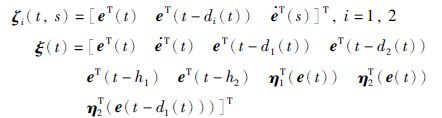
如果Ξ1<0,Ψ1(i)≥0,Ψ2(i)≥0,则由式(24)知对任意的ξ(t)≠0有${\dot V}$(et)<0.
又,由${\dot V}$(et)<0可知V(et)<V(e(0)).
根据引理2,得
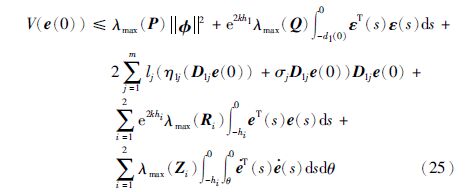
由引理1得
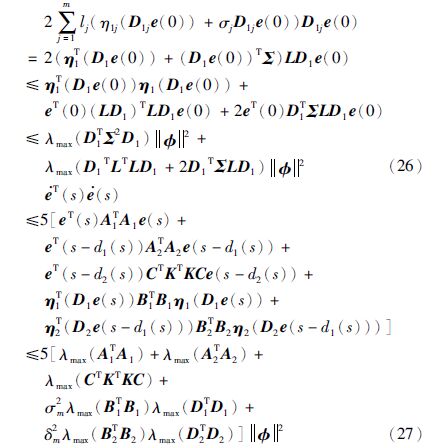
因而,由式(25)、 (26)及(27)得
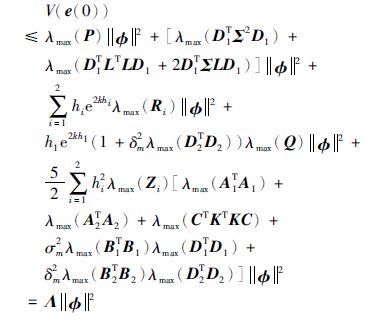
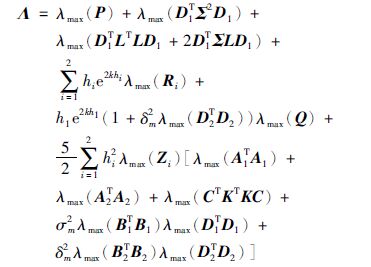
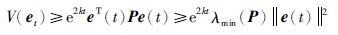
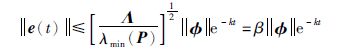
根据引理1,我们下面给出一个采样数据控制器设计的求解方法.
定理2 考虑带有时变时滞d1(t)的驱动系统(1)和响应系统(2),d1(t)满足式(3). 对于给定的标量hi>0(i=1,2),k>0,μ<1和γ,如果存在矩阵$P ≥ 0,Q = \left[ {\begin{array}{*{20}{c}} {{Q_{11}}}&{{Q_{12}}} \\ *&{{Q_{22}}} \end{array}} \right] ≥ 0,{R_i} ≥ 0,{Z_i} ≥ 0,{X^{\left( i \right)}} = \left[ {\begin{array}{*{20}{c}} {X_{11}^{\left( i \right)}}&{X_{12}^{\left( i \right)}} \\ *&{X_{22}^{\left( i \right)}} \end{array}} \right] ≥ 0$(i=1,2),对角矩阵L≥0,U>0,V>0和W>0,以及任意适当维数的矩阵G,F,M(i)=[Mi1T Mi2T]T和N(i)=[Ni1T Ni2T]T(i=1,2),使得下列线性矩阵不等式是可行的
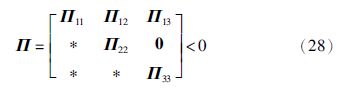

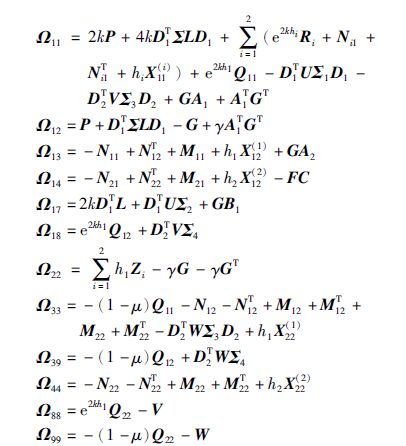
证 令G1=G,G2=γG,F=GK,则由定理1得到结论. 证毕.
注4 定理2为我们提供了带有时变时滞的混沌Lur′e系统(1)和(2)在采样数据控制器(7)作用下指数同步的一个充分条件,所需要的控制器增益可应用Matlab的LMI toolbox求解(28)来获得. 如果取A2=0,B2=0,k=0,$Q = \left[ {\begin{array}{*{20}{c}} {{Q_{11}}}&{{Q_{12}}} \\ *&{{Q_{22}}} \end{array}} \right] = 0$,h1=0,μ=0,则式(28)可应用于文[15, 16, 17, 18]中不含时滞的混沌Lur′e系统同步的情形(见数值仿真). 虽然定理2中的G1=G,G2=γG,F=GK多少带来了一些保守性,且控制器的低频采样数据是以同步性能的降低为代价的(见表 1),但值得提到的是,时滞混沌Lur′e系统的这样一个线性矩阵不等式形式的指数同步判据在文献中还未见报道. 我们期待在以后的研究中能得到更好的结果.
| h2 | 0.01 | 0.03 |
| kmax | 5.95 | 3.96 |
| K | [71.729 5 111.064 5 363.281 3] | [25.820 8 20.965 5 20.333 7] |
| h2 | 0.05 | 0.07 |
| kmax | 2.63 | 1.78 |
| K | [15.757 8 8.697 4 -4.914 1] | [11.337 6 4.746 8 -8.560 2] |
| h2 | 0.09 | 0.11 |
| kmax | 1.21 | 0.79 |
| K | [8.788 0 2.996 9 -8.522 3] | [7.135 0 2.071 4 -7.757 7] |
| h2 | 0.13 | 0.15 |
| kmax | 0.49 | 0.25 |
| K | [3.798 5 3.965 3 -2.458 2] | [5.144 2 1.205 9 -6.116 5] |
| h2 | 0.17 | ≥0.18 |
| kmax | 0.06 | — |
| K | [4.517 5 0.982 4 -5.490 0] | — |
考虑文[26]中的时滞Chua电路分别作为驱动系统和响应系统,它们的方程为
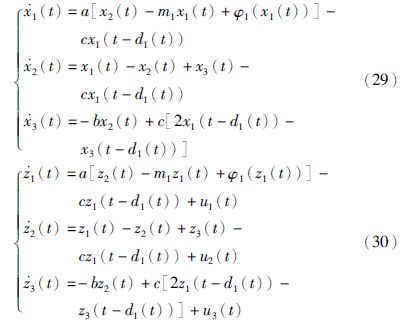
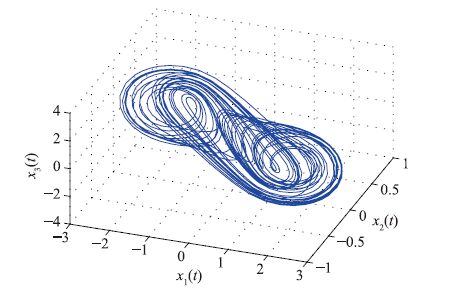
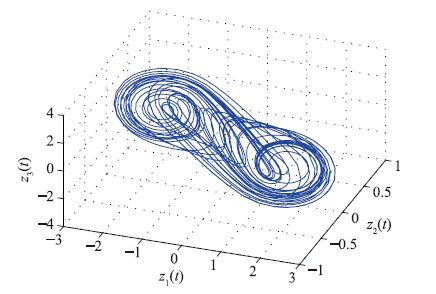
驱动系统(29)和响应系统(30)当分别取初始值x(s)=[0.20.10.3]T和z(s)=[10.5-0.5]T($\forall $s∈[-1,0])时系统呈现出混沌行为,其混沌吸引子的Matlab仿真分别如图 1和图 2所示.
|
| 图 1 驱动系统(29)的混沌吸引子(t∈[0,100]) Fig. 1 Chaotic attractor of drive system(29)(t∈[0,100]) |
|
| 图 2 响应系统(30)的混沌吸引子(t∈[0,100]) Fig. 2 Chaotic attractor of response system(30)(t∈[0,100]) |
系统(29)和(30)可表述成Lur′e系统的形式为
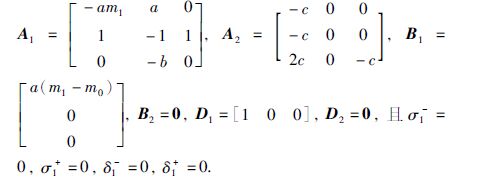
可以验证h1=1,μ=0.25,计算可得σ1=1,δ1=0,Σ=1,Σ1=0,Σ2=0.5,Σ3=0,Σ4=0.
取输出矩阵C=[100],γ=0.15,我们来研究采样间隔与相应的最大指数同步率和控制器增益矩阵之间的关系. 对于不同的采样间隔h2,应用Matlab求解线性矩阵不等式(28),根据定理2计算所得到的最大指数同步率kmax和控制器增益矩阵K的数值如表 1所示. 由表 1可知,随着采样间隔h2的增大,指数同步率变得越来越小. 当采样间隔h2>0.17时,即使指数同步率k=0,控制器也不再存在,也就是说最大允许采样间隔为h2=0.17. 这说明控制器的低频采样数据是以同步性能的降低为代价的,它同时可以指导我们设计控制器时在采样间隔和指数同步率之间权衡以寻求最优的控制器.
当h2=0.09,k=0.1,求解线性矩阵不等式(28)所得控制器增益矩阵为
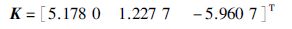
图 3描绘了驱动—响应系统的同步误差e(t)的响应曲线. 可以看出,状态轨迹在有限时间内收敛于0,即,实现了驱动系统(29)与响应系统(30)的指数同步.
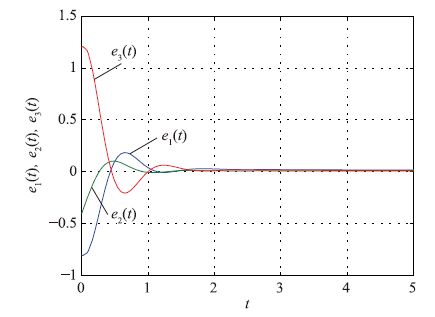
|
| 图 3 h2=0.09且k=0.1时同步误差系统的轨迹 Fig. 3 Trajectories of synchronization error system when h2=0.09 and k=0.1 |
文[15, 16, 17, 18]研究了不含时滞的混沌Lur′e系统基于采样数据控制器(7)的同步问题. 当A2=0和B2=0时,系统(1)和(2)退化为文[15, 16, 17, 18]中的混沌Lur′e系统. 如果令k=0,$Q = \left[ {\begin{array}{*{20}{c}} {{Q_{11}}}&{{Q_{12}}} \\ *&{{Q_{22}}} \end{array}} \right] = 0$,h1=0,μ=0,并取γ=2,则由式(28)可知此时最大采样间隔h2=0.60,相应的控制器增益矩阵为
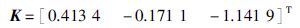
值得注意的是文[15, 16, 17, 18]中的最大采样间隔分别为0.17,0.42,0.21,0.48. 由此可知,由定理2所得到的最大采样间隔比文[15, 16, 17, 18]分别提高了$\frac{{0.60 - 0.17}}{{0.17}}$×100%=252.94%,$\frac{{0.60 - 0.42}}{{0.42}}$×100%=42.86%,$\frac{{0.60 - 0.21}}{{0.21}}$×100%=185.71%,$\frac{{0.60 - 0.48}}{{0.48}}$×100%=25.00%.
5 结论本文研究了带有时变时滞的混沌Lur′e系统同步的采样数据控制问题. 应用自由权矩阵方法和线性矩阵不等式技术得到了采样间隔相关和同步率相关的充分条件,所设计的采样数据控制器能够实现时变时滞混沌Lur′e系统的指数同步. 时滞Chua电路的数值仿真表明指数同步率随采样间隔的增大而减小,这一发现可以指导我们设计控制器时在采样间隔和指数同步率之间权衡以寻求最优的控制器,同时仿真也验证了本文所提出的控制方法的有效性.
| [1] | Pecora L M, Carroll T L. Synchronization in chaotic systems[J]. Physical Review Letters, 1990, 64(8): 821-824. |
| [2] | Nijmeijer H. A dynamical control view on synchronization[J]. Physica D: Nonlinear Phenomena, 2001, 154(3/4): 219-228. |
| [3] | Xiang J, Li Y J, Wei W. An improved condition for master-slave synchronization of Lur'e systems with time delay[J]. Physics Letters A, 2007, 362(2/3): 154-158. |
| [4] | Cheng C J, Liao T L, Yan J J, et al. Synchronization of neural networks by decentralized feedback control[J]. Physics Letters A, 2005, 338(1): 28-35. |
| [5] | Zhang C K, He Y, Wu M. Exponential synchronization of neural networkswith time-varying mixed delays and sampled-data[J]. Neurocomputing, 2010, 74(1/2/3): 265-273. |
| [6] | Park J H. Adaptive control for modified projective synchronization of a four-dimensional chaotic system with uncertain parameters[J]. Journal of Computational and Applied Mathematics, 2008, 213(1): 288-293. |
| [7] | Tang Y, Fang J A. General methods for modified projective synchronization of hyperchaotic systems with known or unknown parameters[J]. Physics Letters A, 2008, 372(11): 1816-1826. |
| [8] | Kuo H H, Hou Y Y, Yan J J, et al. Reliable synchronization of nonlinear chaotic systems[J]. Mathematics and Computers in Simulation, 2009, 79(5): 1627-1635. |
| [9] | Cai N, Jing Y W, Zhang S Y. Modified projective synchronization of chaotic systems with disturbances via active sliding mode control[J]. Communications in Nonlinear Science and Numerical Simulation, 2010, 15(6): 1613-1620. |
| [10] | Gao Y B, Sun B H, Lu G P. Modified function projective lag synchronization of chaotic systems with disturbance estimations[J]. Applied Mathematical Modelling, 2013, 37(7): 4993-5000. |
| [11] | Yahyazadeh M, Noei A R, Ghaderi R. Synchronization of chaotic systems with known and unknown parameters using a modified active sliding mode control[J]. ISA Transactions, 2011, 50(2): 262-267. |
| [12] | Gao Y B, Zhang X M, Lu G P. Dissipative synchronization of nonlinear chaotic systems under information constraints[J]. Information Sciences, 2013, 225: 81-97. |
| [13] | Han Q L. On designing time-varying delay feedback controllers for master-slave synchronization of Lur'e systems[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2007, 54(7): 1573-1583. |
| [14] | Zhong M Y, Han Q L. Fault-tolerant master-slave synchronization for Lur'e systems using time-delay feedback control[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2009, 56(7), 1391-1404. |
| [15] | Lu J G, Hill D J. Global asymptotical synchronization of chaotic Lur'e systems using sampled data: a linear matrix inequality approach[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2008, 55(6): 586-590. |
| [16] | Zhang C K, He Y, Wu M. Improved global asymptotical synchronization of chaotic Lur'e systems with sampled-data control[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2009, 56(4): 320-324. |
| [17] | Zhu X L, Wang Y Y, Yang H Y. New globally asymptotical synchronization of chaotic Lur'e systems using sampled data[C]//2010 American Control Conference. Piscataway, NJ, USA: IEEE, 2010. |
| [18] | Zhang C K, Jiang L, He Y, et al. Asymptotical synchronization for chaotic Lur'e systems using sampled-data control [J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(10): 2743-2751. |
| [19] | Wu Z G, Shi P, Su H Y, et al. Sampled-data synchronization of chaotic Lur'e systems with time delays[J]. IEEE Transactions on Neural Networks and Learning Systems, 2013, 24(3): 410-421. |
| [20] | Chen W H, Wei D, Lu X M. Global exponential synchronization of nonlinear time-delay Lur'e systems via delayed impulsive control[J]. Communications in Nonlinear Science and Numerical Simulation, 2014, 19(9): 3298-3312. |
| [21] | Fridman E, Seuret A, Richard J. Robust sampled-data stabilization of linear systems: an input delay approach[J]. Automatica, 2004, 40(8): 1441-1446. |
| [22] | He Y, Wu M, She J H. Delay-dependent exponential stability of delayed neural networks with time-varying delay[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2006, 53(7): 553-557. |
| [23] | Zhang Q, Wei X, Xu J. Delay-dependent exponential stability of cellular neural networks with time-varying delays[J]. Chaos, Solitons & Fractals, 2005, 23(4): 1363-1369. |
| [24] | Khalil H K. Nonlinear Systems[M]. Beijing: Publishing House of Electronics Industry, 2007. |
| [25] | Liu Y R, Wang Z D, Liu X H. Design of exponential state estimators for neural networks with mixed time delays[J]. Physics Letters A, 2007, 364(5): 401-412. |
| [26] | Gao Y B. Dissipative control of time-delay chaotic systems via DOBC approach[C]//Proceedings of the 31st Chinese Control Conference. Hefei: University of Science and Technology of China, 2012. |



