1 引言
配料过程是冶金、 化工、 钢铁、 水泥等许多流程工业的一道重要工序,其原料配比的合理性不仅有助于稳定配料产品质量,降低原料成本,而且对于后续工序产品质量的提高和能源消耗的降低有重要的影响. 因此,实现有效的配料过程优化控制,对企业的生产的稳定和节能降耗都具有重要意义.
由于资源和能源的日益紧张和工业过程的复杂性[1],配料过程的优化控制已成为许多过程控制领域学者的研究内容. 线性规划和非线性规划是配料过程优化的经典方法[2, 3]. 但线性规划仅能够解决小规模线性配料过程的优化问题. 对于大规模、 非线性的复杂配料过程,许多学者将神经网络和专家系统等智能技术用于非线性建模和优化计算过程[4, 5, 6, 7, 8]. 尽管这些智能方法在配料过程优化控制中发挥了重要作用,但这些方法都是在输入数据已知并等于某些标称值的假设条件下建立模型来寻找最优解,没有考虑过程参数不确定性的影响[9, 10]. 实际上,大多数流程工业配料过程的原料成分参数都存在不同程度的不确定性,这种不确定性使得基于传统优化方法所获得的优化结果变得不可行,在实际生产中,可能造成资源能源的巨大浪费和生产的不稳定. 为了考虑这种不确定性,灵敏度分析、 鲁棒优化和随机规划被应用到工程优化问题中[11]. 灵敏度分析主要用来测量数据的不确定性对优化结果的影响; 鲁棒优化[12, 13, 14]研究参数在某个不确定集合内具有最坏情况值的不确定问题; 在随机规划中,不确定参数用概率分布来表示,将其直接引入优化模型中进而进行优化计算. 随机规划处理不确定参数的直接性使其在不确定工业优化过程中得到了广泛应用[11, 15]. 本文结合流程工业配料过程的特点,主要考虑原料成分参数的不确定性,建立配料过程的随机规划模型; 并利用一种高效的抽样技术——HSS(Hammersley sequence sampling)[16, 17]——获得不确定随机优化模型对应的期望值优化模型; 同时,也将HSS技术引入遗传算法,以保证进化过程中种群分布的均匀性,实现随机优化问题的优化求解. 最后结合某冶金配料过程的工业运行数据进行基于所提出方法的优化计算,优化结果表明了方法的可行性和有效性.
2 配料随机优化模型在大多数流程工业配料过程中,由于原料矿源不稳和成分检测滞后,原料质量参数存在时变性且难以实时获得确定值,因此只能采用随机数来描述; 另外,配料过程的最基本要求是保证产品质量,也就是使配料产品的质量指标与工艺要求相符合,在满足了这一技术要求后,最直接的要求就是降低成本. 因此,本模型以原料消耗成本最小为目标函数,以质量指标等工艺要求为约束,同时将原料成分的不确定性以随机数的形式引入指标约束中,建立流程工业配料过程的随机优化模型.
2.1 决策变量设参与配料的原料有m种,xi为第i种原料的配入量,每种原料的配入量x1,x2,…,xm是决策变量,令:
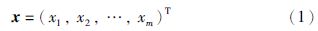
设ci为第i种原料的价格,目标函数可写为
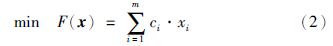
在流程工业配料过程中,配料产品的质量参数通常被要求控制在给定的一个理想变化区间,通过调整原料配比要求产品质量指标尽可能在要求区间范围内. 这些质量指标除了与原料配比有关,还会受到每种原料中有效成分的影响. 但由于检测的滞后性,这些成分参数无法实时获得,这里将原料成分参数以随机数的形式引入到指标约束中,以考虑原料质量参数不确定性的影响.
(1) 产品质量指标约束. 设配料产品质量的性能指标有n个,qkmin和qkmax分别为第k个指标的下限值和上限值,则产品质量约束可以表示为
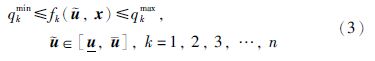
(2) 总量约束. 在配料过程中,投入的原料越多,产量越大,但考虑实际的生产能力,产量通常会有限制,设允许的最大产量M,约束方程为

(3) 非负约束.

综合式(1)~(5),在保证产品质量的前提下,以降低原料消耗费成本为目标的配料随机优化模型可表示为
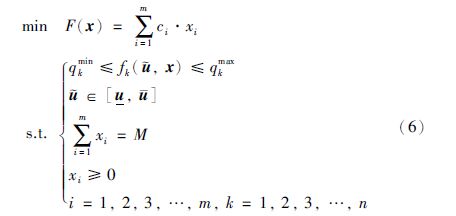
在模型(6)中,fk($\tilde u$,x)是核心,它描述配料产品第k个指标与原料质量$\tilde u$和配比x之间关系,其形式取决于具体过程的特性,可以为线性或非线性,也可以是类似神经网络的智能模型.
3 基于HSS技术的期望值模型对于不确定参数为连续分布的优化问题,抽样近似是获得等价确定性模型的最常用方法. 考虑传统MCS(Monte Carlo sampling)技术[18, 19]具有样本误差大、 收敛速度慢等缺点,这里采用高效的HSS技术,获得随机优化模型对应的期望值优化模型.
HSS技术就是采用一种利用超均匀随机序列Hammersley sequence来代替MCS中的伪随机序列,并采用最优的设计方案在K维超立方体中放置n个数据点,以确保样本集更具代表性和多维均匀性,提高抽样收敛速度[17]. 设随机优化模型式(6)中的配料原料成分矩阵$\tilde u$中共有K个非零元素,采用HSS技术获得对应期望值优化模型的步骤如下:
(1) 令j=1,取K-1个不同的素数Ri(i=1,2,…,K-1);
(2) 利用HSS技术从超立方体[0,1]K中产生第j个样本φK(j);
(3) 将原料成分参数矩阵$\tilde u$中的非零元素用φK(j)中的K个元素分别替换,构造Hammersley sequence矩阵z(j);
(4) 令udhj=udh+zdh(j)·($\bar u$dh-udh),得到不确定变量矩阵$\tilde u$的第j个样本uj={udhj},下标dh表示相应矩阵第d行第h列的元素;
(5) 令j=j+1,重复步骤(2)~(5)共Nsamp次;
(6) 将抽样产生的不确定矩阵$\tilde u$的Nsamp个样本,按式(7)构造与式(6)相对应的期望值优化模型:
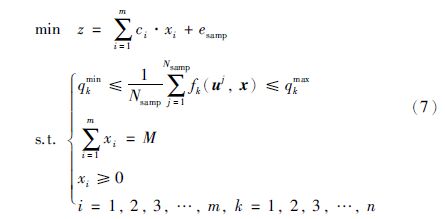
对于不满足凸条件、 超大规模或者解空间不连续的优化问题,遗传算法是一个有效的求解方法[20]. 这里,为了改善种群的多样性、 均匀性和算法的收敛速度,将HSS应用于遗传算法进化过程中,采用一种HSS随机遗传算法实现配料随机优化问题的求解.
4.1 染色体编码决策向量x=(x1,x2,…,xm)即为染色体,在进行交叉和变异时,仅选择一个变量xi为操作变量,且变异时对该变量采用二进制编码.
4.2 种群初始化设群体规模为NP,利用HSS抽样方法从超立方体[0,1]m中均匀生成NP个样本,则第1个样本可表示为
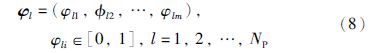
初始种群中第l个染色体的第i个元素可初始化为
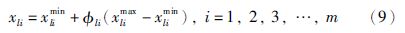
首先,随机生成一个初始样本数,在GA进化过程中不断更新:
if rand(0,1)≤0.5,then
Nsamp=Nsamp+10·rand(0,1)
Nsamp=Nsamp-10·rand(0,1)
根据优化目标函数和约束条件,构造如下适应度函数:

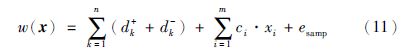
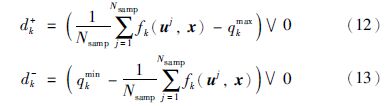
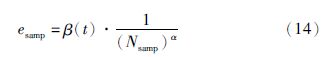

HSS随机遗传算法的步骤如下:
(1) 利用HSS方法生成初始种群P(t).
(2) 选择抽样样本数Nsamp.
(3) 采用适应度函数(10)评价P(t).
(4) 如果终止条件满足,输出结果; 否则,利用HSS技术产生交叉和变异概率,进行选择、 交叉和变异,产生新的种群,重复步骤(2)~(4).
5 工业应用实验为说明模型和算法的有效性,以某铝业公司氧化铝生料浆配料过程为例进行现场跟踪优化计算,该过程更详细的描述见文[5]. 在该过程中,原料中各种有效成分含量不稳定且无法实现在线检测,这些具有不确定性的原料质量参数将被视为随机数. 该过程参与配料的原料有4种不同品位的铝矿石、 石灰、 碱粉、 煤及从后续工序返回的碱液和硅渣,共9种原料,所以随机优化模型(6)中m=9. 配料产品(生料浆)的质量指标主要有铝硅比、 碱比、 钙比三个参数,即n=3. 若f1($\tilde u$,x)为铝硅比的函数、 f2($\tilde u$,x)和f3($\tilde u$,x)分别为碱比的函数和钙比的函数,有:
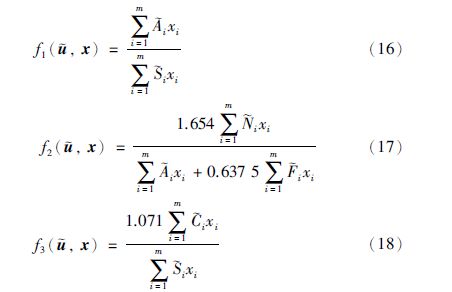

利用该配料过程的运行数据,采用随机优化模型进行优化计算,并将优化结果与前期开发的确定性优化方法[21]进行比较,结果如图 1和表 1所示.
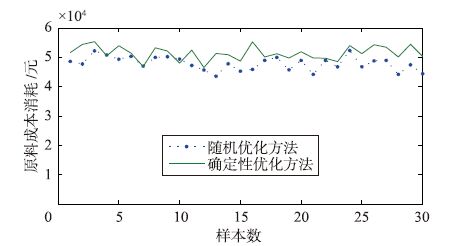
|
| 图 1 原料消耗成本对比 Fig. 1 Comparison of the raw material cost |
| 质量指标 | 随机优化方法 | 确定性优化方法 |
| 铝硅比f1 | 95.48% | 95.63% |
| 碱比f2 | 98.04% | 97.52% |
| 钙比f3 | 94.34% | 90.23% |
图 1为随机优化方法和确定优化方法的原料消费成本比较曲线. 从图 1可以明显看出,随机优化方法可以获得更小的消耗成本,这是因为随机优化模型是以原料成本消耗最小为直接优化目标,而确定性优化方法是以配料产品指标为优化目标的. 表 1比较了两种优化方法配制的生料浆质量指标合格率,可以看出采用随机优化方法配制的生料浆碱比和钙比的合格率不劣于确定性优化方法,特别提高了碱比和钙比的合格率,说明随机优化方法具有较好的鲁棒性. 造成铝硅比合格率降低的主要原因是由于确定性优化方法是以3个质量指标为优化目标的,而且设定了铝硅比为一级优化指标,而随机优化方法将成本作为优化目标,在优化计算过程中,会加大低成本物料(即返回硅渣和碱液)的用料量的用料量,而尽量节约铝含量较高的矿石的使用.
可见,采用所提出的随机优化方法进行配料,在原料质量存在不确定性的情况下,既能够保证产品质量指标满足要求,又能够有效减低原料消耗成本,说明优化结果更具鲁棒性.
6 结论(1) 针对一类流程工业配料过程具有质量指标多、 原料参数不确定等特点,以原料消耗成本最小为直接优化目标,将不确定参数作为随机数引入质量指标约束方程,建立了一种配料过程随机优化模型. 该模型既能在不确定环境下保证多个质量指标同时满足生产要求,而且兼顾了原料成本的消耗和生产能力的限制.
(2) 将高效的HSS技术应用于期望值优化模型转化和遗传算法的种群初始化和交叉、 变异操作中,保证了每一代种群分布的均匀性,同时,将HSS相应的抽样误差惩罚项引入适应度函数中,实现了随机优化模型快速有效的求解.
(3) 工业实验应用结果表明,提出的随机优化方法能够在不确定环境下保证各个质量指标满足生产要求,而且能够有效降低原料的消耗成本,优化结果具有较好的鲁棒性.
| [1] | 史洪岩, 苑明哲, 黄明忠, 等. 基于最优控制方法的生物柴油酯交换过程的温度优化[J]. 信息与控制, 2013, 42(6): 772-777, 784. Shi H Y, Yuan M Z, Huang M Z, et al. Optimization of temperature for biodiesel transesterification processes based on optimal control approach[J]. Information and Control, 2013, 42(6): 772-777, 784. |
| [2] | 杨秋辉, 游志胜, 樊鸿, 等. 用线性规划求解工程混合料最优配料问题[J]. 四川大学学报: 自然科学版, 2005, 42(1): 198-201. Yang Q H, You Z S, Fan H, et al. The using of programming solution in optimal mix design in highway engineering[J]. Journal of Sichuan University: Natural Science Edition, 2005, 42(1): 198-201. |
| [3] | 贾娟鱼, 白晨光, 赖宏, 等. 烧结矿和入炉矿配料的优化及实现[J]. 重庆大学学报: 自然科学版, 2002, 25(10): 68-71. Jia J Y, Bai C G, Lai H, et al. Optimization and realization for sinter and ore blending for blast furnace[J]. Journal of Chongqing University: Natual Science Edition, 2002, 25(10): 68-71. |
| [4] | Wen Y, Morales A. Neural networks for the optimization of crude oil blending[J]. International Journal of Neural Systems, 2005, 15(5): 377-389. |
| [5] | Yang C H, Gui W H, Kong L S, et al. Modeling and optimal-setting control of blending process in a metallurgical industry[J]. Computers and Chemical engineering, 2009, 33(7): 1289-1297. |
| [6] | 阳春华, 沈德耀, 吴敏, 等. 焦炉配煤专家系统的定性定量综合设计方法[J]. 自动化学报, 2000, 26(2): 226-232. Yang C H, Shen D Y, Wu M, et al. Synthesis of qualitative and quantitative methods in a coal blending expert system for coke oven[J]. Acta Automatica Sinica, 2000, 26(2): 226-232. |
| [7] | 白锐, 柴天佑, 马恩杰. 生料浆配料过程综合自动化系统[J]. 系统仿真学报, 2007, 19(11): 2594-2598. Bai R, Chai T Y, Ma E J. Integrated automation system for raw slurry blending process[J]. Journal of System Simulation, 2007, 19(11): 2594-2598. |
| [8] | Duan X G, Yang C H, Li H X, et al. Hybrid expert system for raw materials blending[J]. Control Engineering Practice, 2008, 16(11): 1364-1371. |
| [9] | Chai T Y, Qin S J, Wang H. Optimal operational control for complex industrial processes[J]. Annual Reviews in Control, 2014, 38(1): 81-92. |
| [10] | Engell S. Feedback control for optimal process operation[J]. Journal of Process operation, 2007, 17(3): 203-219. |
| [11] | Zhang Y, Dayadeep M, Forbes J F. Real-time optimization under parametric uncertainty: A probability constrained approach[J]. Journal of Process Control, 2002, 12(3): 373-389. |
| [12] | Wei P, Rene V M, Syed I. A robust optimization approach for real-time multiple source drinking water blending problem[J]. Journal of Water Supply: Research and Technology-AQUA, 2012, 61(2): 111-122. |
| [13] | Jorge S J, Meriam C. Robust real-time optimization for the linear oil blending[J]. RAIRO Operations Research, 2013, 47(4): 465-479. |
| [14] | Wiebenga J H, Klaseboer G, van den Boogaard A H. Theory and applications of robust optimization[J]. Society for Industrial and Applied Mathematics, 2011, 53(3): 464-501. |
| [15] | Shih J S, Christopher F H. Coal blending optimization under certainty[J]. European Journal of Operational Research, 1995, 83(3): 452-465. |
| [16] | Kong L S, Yang C H, Xiao S P, et al. Stochastic optimization method based on HSS technique and expert knowledge for a metallurgical blending process[C]//3th International Conference on Intelligent System Design and Engineering Applications. Piscataway, NJ, USA: IEEE, 2013: 1290-1293. |
| [17] | Ponce-Ortega J M, Vicente R R, Salvador H C, et al. Improving convergence of the stochastic decomposition algorithm by using an efficient sampling technique[J]. Computers and Chemical Engineering, 2004, 28(5): 767-773. |
| [18] | Wolfgang J. Quasi-Monte Carlo sampling to improve the efficiency of Monte Carlo EM[J]. Computational Statistics & Data Analysis, 2005, 48(4): 685-701. |
| [19] | Wang S B, Wang Y L, Liu B, et al. A hybrid sequence sampling technique and its application to multi-objective optimization of blending process[C]//30th Chinese Control Conference. Piscataway, NJ, USA: IEEE, 2011: 2135-2140. |
| [20] | Diwekar U M, Xu W. Improved genetic algorithm for deterministic optimization and optimization under uncertainty, Part I: Algorithms development[J]. Industrial &Engineering Chemistry Research, 2005, 44(18): 7132-7137. |
| [21] | 孔玲爽, 阳春华, 朱红求, 等. 基于专家知识的字典序优化决策方法及工业应用[J]. 控制与决策, 2009, 24(12): 1909-1911, 1916. Kong L S, Yang C H, Zhu H Q, et al. Expert-knowledge-based lexicographic order optimal decision method and its industrial application[J]. Control and Decision, 2009, 24(12): 1909-1911, 1916. |



