2. 上海大学计算中心, 上海 200444
2. Computing Center, Shanghai University, Shanghai 200444, China
1 引言
引耗散性是动态系统分析和综合中的一个重要概念[1, 2],它从能量的角度反映了实际工程系统输入信号和输出信号之间的内在关系. 耗散系统理论为控制系统的分析和设计提供了一个完整的理论框架,并且在互联系统的稳定性判别与设计中有着重要的实际应用价值[3, 4, 5]. 正实系统(也称为无源系统)和有界实系统(也称为收缩系统或小增益系统)作为两类常见的耗散系统受到了广泛的关注,目前已形成了一系列相关的理论分析和设计方法. 由于耗散理论在应用上的重要性. 长期以来一直是系统及控制相关研究的热门领域之一.
负虚系统理论是近年来新发展起来的一个与耗散系统理论密切相关的研究方向. Lanzon等最早在文[6]中发现当柔性结构机械系统中的位置传感器与受力执行器采用共位安装时,系统将不具有正实性,但同时系统传递函数满足负虚性,这一特性同样可以用于判别互联系统的稳定性. 文[7]中,Petersen进一步详细地给出了负虚性的物理意义并描述了若干常见的满足负虚性的电路系统和机械系统. 负虚性的提出为控制系统的分析和设计提供了一个新的思路. 与正实系统理论类似,负虚系统理论很快被应用到采用反馈连接[6, 7, 8]、 环形连接[9]及事件驱动连接[10]等各类情形下的互联系统的稳定性分析中. 此外,文[11, 12]等还讨论了利用负虚理论来进行控制器设计的相关问题; 文[13]和文[14]分别给出了负虚广义系统和负虚无穷维系统的负虚性分析结果; 根据文[15, 16, 17, 18]中建立起的线性系统有限频分析理论,Xiong等在文[19]进一步丰富了负虚性质的内涵,提出了有限频负虚性的概念; 在文[20]中,liu和Xiong还提出了更为广义的α和D负虚性概念. 这些快速发展的负虚系统理论相关成果为控制系统的分析和综合提供了一套方案,有利地补充了以正实性(无源性)等为基础的耗散系统理论方法.
时滞是一类在网络控制、 电路、 机械、 建筑结构、 化工过程等诸多领域里的常见现象[21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41]. 事实上,从系统理论的观点来看,许多实际系统的过去状态都会对其当前状态产生一定的影响,即系统的演化不仅由当前状态决定,还依赖于过去某一时刻或若干时刻的状态,符合这类性质的系统就被称为时滞系统[22]. 由于时滞系统极其广泛的实际应用背景,在过去20多年中有大量研究人员投入到时滞系统的相关研究中,并出现了相当丰富的研究结果,已建立起相对完善的稳定性分析理论和控制设计方法[21, 22, 23]. 同时,关于时滞系统的耗散性分析也有一些结果见诸报道,文[24, 25, 26]分别给出了时滞系统有界实性和正实性等耗散性的时滞相关及时滞无关型判据. 文[27, 28, 29]考虑了使得线性闭环时滞系统满足正实性质的正实控制问题,给出了正实控制器的设计方法. 文[30, 32, 33]分别就广义时滞系统、 随机时滞系统、 模糊时滞系统等复杂时滞系统的正实化控制问题进行了研究,给出了相应的设计方法. 文[34, 35]分析了无源系统在通过带有通信时延的信道互联时的稳定性和无源性等问题. 但对于和正实性密切相关的负虚特性,目前还没有文献针对时滞系统给出相应的判据或其它理论分析结果.
本文考虑连续时间线性时滞系统的负虚性分析问题. 首先从标准线性系统的相关定义出发,对时滞系统的负虚性及有限频负虚性进行了定义. 通过引入Jensen不等式等一些对线性系统时滞项的有效技术手段,成功地根据系统的频域模型出发推导出了时滞系统满足负虚性及有限频负虚性的充分性条件,进而可利用现有的线性矩阵不等式求解工具来实现时滞系统负虚性的判别. 该结果的有效性和正确性通过一个数值算例得到了进一步的验证和说明.
符号说明: 本文中MT表示矩阵M的转置,M*表示矩阵M的共轭转置,M>0表示M为正定矩阵. 矩阵或矩阵不等式中的“*”表示相应的矩阵对称项. ⊗表示克劳内克乘积运算.
2 问题描述与预备知识考虑如下方程描述的带有状态时滞的连续时间线性系统:
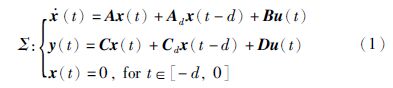
令U(s)、 X(s)和Y(s)分别为信号u(t)、 x(t)和y(t)经拉普拉斯变换后的形式,则系统在频域的表现形式为
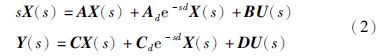
线性时滞系统(1)从输入信号u(t)到输出信号y(t)的传递函数为
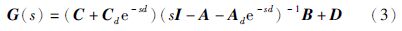
定义1(线性时滞系统的负虚性) 当时滞系统(1)满足下列两个条件时,称时滞系统(1)为负虚系统:
(1) 时滞系统(1)为渐近稳定系统;
(2) 对任意ω>0,下列负虚特征不等式:
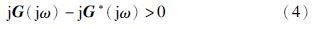
定义2(线性时滞系统的有限频负虚性) 当时滞系统(1)的传递函数G(s)对任意0<ω<$\tilde \omega $l都满足不等式jG(jω)-jG*(jω)>0,则称时滞系统(1)为频率区间ω∈(0,$\tilde \omega $l)的有限频负虚系统.
本文的主要研究目标为给出线性时滞系统(1)的负虚性和有限频负虚性的判据,找到合理的数值计算方法来检验定义1和定义2中涉及到无限多频率点上的不等式.
下列不等式将在本文结果的推导中发挥重要作用.
引理1(Jensen不等式引理[23]) 对任意给定对称正定矩阵R=R*>0及任意在区间(a,b)上的可微信号ω,下列不等式成立:
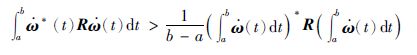
首先来考虑问题1,即线性时滞系统(1)的分析问题. 下列定理给出了的相关分析结果.
定理1(线性时滞系统的负虚性判据) 考虑式(1)给出的线性时滞系统,如果矩阵D为对称矩阵且存在对称矩阵P、 M1、 M2、 N1、 N2,其中P≥0,M1≥0,M2≥0,使得下列线性矩阵不等式成立:
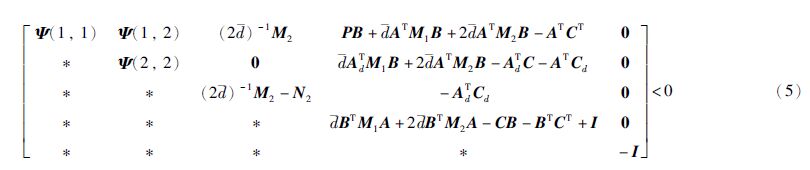
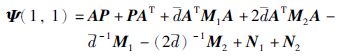

证明 由于这里要求矩阵D为对称矩阵,因此等式(jω)D-(jω)DT=0恒成立,进而可以将不等式(5)改写为下列形式:
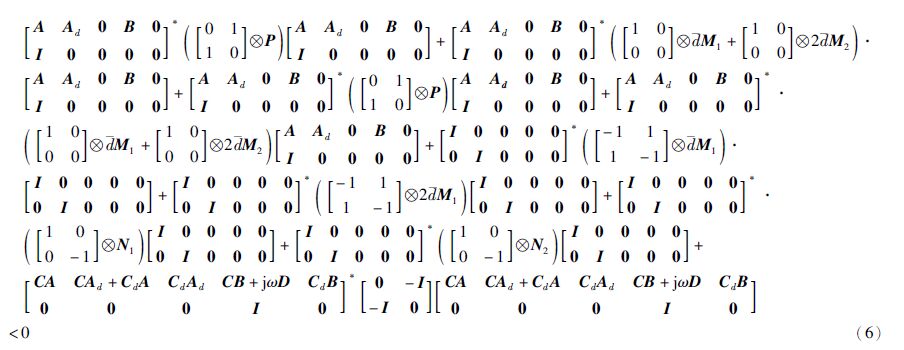
考虑取s=jω的情形,由时滞系统模型在复频域的表现形式可得
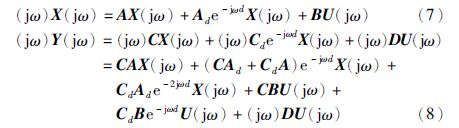
在不等式(6)两边分别乘以向量[X*(jω) ejωdX*(jω) ej2ωdX*(jω) U*(jω) ejωdU*(jω)]和其转置,结合频域方程(7)、 (8)可得

由于不等式(5)中的决策变量满足M1>0,M2>0,因此对任意的d≤d都有:
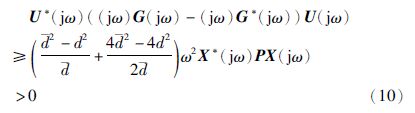
进一步可知:
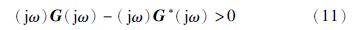
从式(11)可以明显看出,对任意的ω≥0,定义1中的负虚特征不等式(4)均成立.
接下来证明满足负虚特性的时滞系统(1)的稳定性. 与证明负虚性质有所不同,本文从将时域的角度来给出稳定性的证明. 考虑下列形式的李亚普诺夫函数:
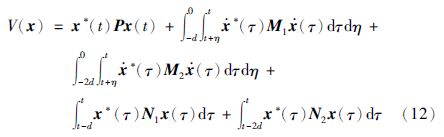
对该李亚普诺夫函数进行求导可得:
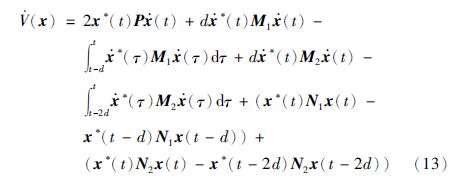
利用Jensen不等式可知:
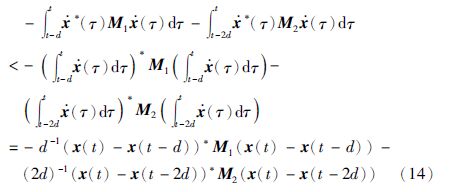
现在令Φ表示定理1中不等式(5)左边的矩阵,根据式(13)、 (14)可进一步推出:

由李亚普诺夫稳定性原理可知时滞系统(1)为稳定系统. 证毕.
注1 定理1通过一个线性矩阵不等式给出了时滞系统耗散性判据设计条件,而线性矩阵不等式是否存在可行解的判别问题是一个凸优化问题,可以利用Matlab的LMI工具箱进行验证求解. 这就将对无穷多个频率点处的负虚性判断变成了一个通过有限步骤数值计算即可解决的问题.
注2 从定理1关于负虚性的证明过程中可以看出,当对称矩阵变量P、 N1、 N2不满足正定性时也能够保证频域不等式jG(jω)-jG*(jω)>0成立; 但从稳定性的证明看,非正定的P、 N1、 N2则无法保证系统的稳定性. 如果不等式(5)中的变量P、 N1、 N2无正定性要求,则需要另外新增加一个不等式来进行稳定性的判别,这样可以减小定理1只采用一个不等式的保守性,但同时会相应地增加计算量.
注3 针对不带有时滞项的标准线性系统,文[6]中给出的负虚性判据为充分必要判据. 与之不同,针对本文所讨论的线性时滞系统,定理1仅给出了一个充分性的负虚性判据. 事实上对时滞系统的各类分析及综合问题均很难给出充分必要性的结果. 另外当时滞项为0时,可令定理1中的变量M1、 M2、 N1、 N2为0,此时定理1中的不等式将退化为线性系统时的负虚引理[6].
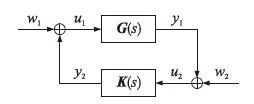
注4 探讨时滞系统的负虚性质及其判据不仅具有理论上的价值,同时也有着重要的实际意义. 判别系统是否具有负虚性不仅有利于深入了解系统的耗散特性,更重要的是可用于判断如下图 1所示的一些常见互联反馈系统的稳定性.
|
| 图 1 负虚互联反馈系统 Fig. 1 Interconnected feedback system with negative imaginary |
图 1中的G(s)表示被控对象,K(s)表示相应的控制器. 考虑图 2所示的悬臂梁控制系统[11],以悬臂梁的输入端电级的端电压vx为输入信号、 输出端电极的端电压vy为输出信号、 则悬臂梁控制系统的输入输出关系可表示为vy=Gxy(s)vx,其中
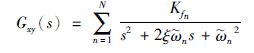

|
| 图 2 悬臂连控制系统 Fig. 2 Cantilever beam control system |
在这里表示这类单输入单输出系统传递函数,参数Kfn、 ξ及$\tilde \omega $n(n=1,…,N)分别表示系统的增益、 阻尼率和自然频率. 通常而言,具有微耦合结构的柔性机械系统[6, 7, 8, 11, 12]以及一些特殊结构的电路系统[7]的传递函数均可以用类似的形式表示. 根据负虚性的定义可知,这类对象本身满足负虚性[6, 7, 8]. 众所周知,设计和评价一个控制器K(s)的首要条件为相应的闭环系统是否稳定,根据文[6, 8, 9]中的结果,当被控对象G(s)为负虚系统时,如果控制器K(s)同样具有负虚性且两者的零频响应乘积小于1,则闭环系统为稳定系统. 因此,在这类情形下,对控制器K(s)是否具有负虚性的判别和刻画就具有非常重要的现实意义. 一方面,这类被控对象往往动态特性复杂、 模型级数很高(如文[37]中的悬臂连实例中的对象模型阶数高达110阶),直接对闭环系统整体进行相应的稳定性判别所需的计算复杂度很高; 另一方面,根据负虚互联系统理论,此时可通过对控制器K(s)的负虚性判别来实现闭环系统稳定性的判别,这样可以大大降低所需的计算复杂度. 特别是当互联系统中带有传输延时或者采用带记忆结构的控制律时[28, 35, 38],控制器K(s)可表示为如式(1)所示的线性时滞系统,因此研究时滞系统的负虚性判别条件非常必要. 本文定理1给出的判据不仅可以用于时滞系统的负虚性判别,同时还为设计满足负虚性的时滞控制器奠定了理论基础.
正如在文[15, 16, 17, 18, 19]中所述,一些实际系统可能不满足任意频率上的负虚性或者正实性等要求,但可能会满足某一给定频率区间上的负虚性等性质. 考虑到许多实际系统的工作频率范围常常是有限的区间,也即输入信号为某一频率区间内的有限频信号,因此对系统在有限频域下的负虚性等性质进行分析也具有重要的现实意义. 下面给出关于线性时滞系统有限频负虚性分析的一个结果.
定理2(线性时滞系统的有限频负虚性) 考虑式(1)给出的线性时滞系统,如果存在对称正定矩阵Q、 M1、 M2和对称矩阵P、 N1、 N2使得下列线性矩阵不等式成立:
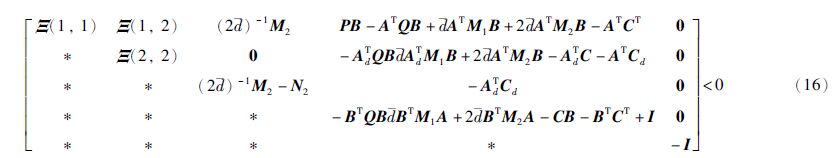
其中,
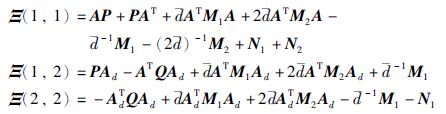
证明定理2的证明和定理1的证明过程类似,区别就在于增加了与频率区间上界相关的矩阵变量. 为完整起见,这里给出了证明的详细过程. 首先对不等式(14)进行整理,可得
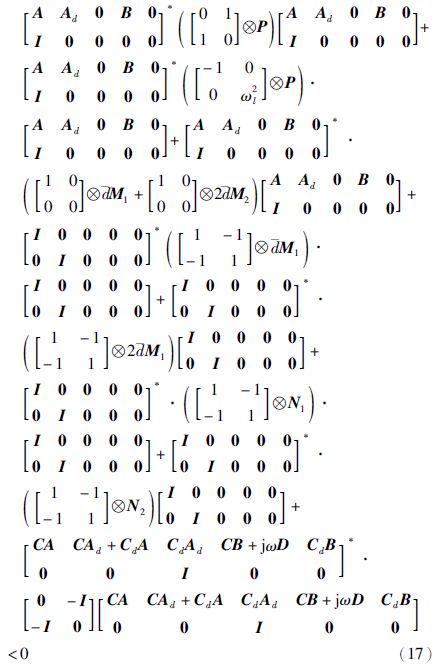
同样的,在不等式(17)两边分别乘以向量[X*(jω) ejωdX*(jω) ej2ωdX*(jω) U*(jω) ejωdU*(jω)]和其转置,结合频域方程(7)、 (8)可得

注意到,当0<ω<$\tilde \omega $l时,($\tilde \omega $l2-ω2)>0. 由Q>0,M1>0,M2>0,并结合定理1中的证明过程可知,Q>0,M1>0,M2>0. 当0<ω<$\tilde \omega $l时,频域不等式(jω)G(jω)-(jω)G*(jω)<0恒成立. 证明完毕.
注5 定理2给出了时滞系统有限频负虚性的一个充分性判据. 与全频负虚性相比,有限频负虚性在定义中没有要求时滞系统(1)必须为稳定系统,因此定理2给出的判据是无法说明系统稳定性的. 在文[19]中,Xiong等通过引入文[16, 17]中的有限频性能时域分析方法对有限频负虚性的物理意义给出了相应的说明和解释,对时滞系统而言,这一时域说明同样适用.
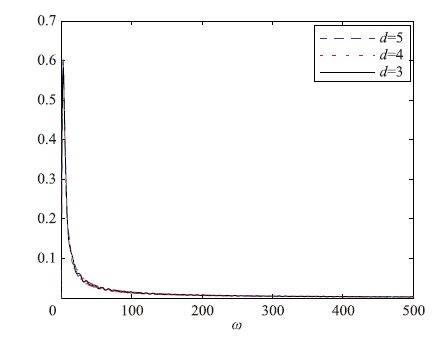
4 算例例1 考虑式(1)给出的一个线性时滞系统G1(jω),其参数矩阵给定如下:
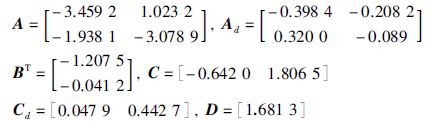

|
| 图 3 当0<ω<6.18时,时滞系统G1(jω)的负虚频域特征函数(即j(G1(jω)-G*1(jω)) Fig. 3 Curves of the 0<ω<6.18 negative imaginary characterization function of the time delayed system time G1(jω) (i.e. j(G1(jω)-G*1(jω))) |
从图 3可以看出,时滞系统G1(jω)满足定义1中的频域不等式约束,而且由定理1的证明可知该系统同时为稳定系统.
例2 现在考虑参数为下列矩阵的线性时滞系统G2(jω):
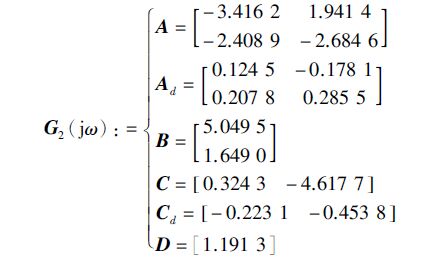
假设已知其延时上界为d=0.8. 采用定理1对其进行负虚性判别,无法找到可行解. 由于定理1中的判别条件为充分性条件,所以这本身并不能说明该系统一定不具有负虚性. 现在改用定理2来分析其有限频负虚性,利用Matlab的LMI工具箱,可以在设定频率范围小于$\tilde \omega $l=6.18的情况下找到可行解. 其中当令$\tilde \omega $l=6.18时不等式(16)的一组可行解为

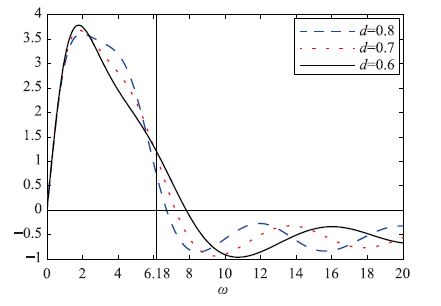
根据定理2至少可以确定: 当0<ω<6.18时,该时滞系统满足负虚频率不等式(4). 为进一步直观地说明这一有限频域内的负虚性质,图 4给出了当时滞长度分别为d=0.8,0.7,0.6时的系统负虚特征函数曲线.
|
| 图 4 时滞系统G2(jω)的负虚频域特征函数(即j(G2(jω)-G*2(jω)) Fig. 4 Curves of the negative imaginary characterization function of the time delayed system G2(jω)(i.e. j(G2(jω)-G*2(jω))) |
从图 4中可以看出,当d≤d=0.8时,系统在由定理2确定的频率区间(0<ω<6.18)满足负虚定义中的频域不等式(4). 在图 4中,系统实际上满足负虚定义不等式(4)的频率区间要略大于由定理2确定的频率区间,这是由于定理2中不等式仅为判别有限频负虚性的充分性条件,必然存在一定的保守性,从该例的计算结果来看,定理2在有限频负虚性质判定上的保守性很小,可以在实际中给出一个较满意的负虚频率区间估计下界.
5 结语本文探讨了连续时间线性时滞系统的负虚性分析问题. 结合标准线性系统情形下的相关理论,首先给出了时滞系统负虚性及有限频负虚性的定义. 从时滞系统的频率特性出发,结合Jensen不等式等技术给出了判别其是否具有负虚性及有限频负虚性的充分性条件,进而可利用Matlab通过求解一个线性矩阵不等式的可解性问题来实现时滞系统负虚性以及有限频负虚性的分析问题. 仿真算例说明了所给判据的有效性. 本文结果为未来进一步研究互联负虚时滞系统的设计问题以及时滞系统的负虚化控制器设计问题提供了初步的理论分析结果.
| [1] | Lozano R, Maschke B, Egeland O. Dissipative systems analysis and control[M]. Berlin, Germany: Springer-Verlag, 2007. |
| [2] | Nicholas K, Michael J M, Xia M, et al. On relationships among passivity, positive realness, and dissipativity in linear systems[J]. Automatica, 2014, 50(4): 1003-1016. |
| [3] | Hurtado Q, Rodrigo H, Griggs W M, et al. On interconnected systems, passivity and some generalisations[J]. International Journal of Control, 2013, 86(12): 2274-2289. |
| [4] | Romeo O, Garcia-Canseco E. Interconnection and damping assignment passivity-based control: A survey[J]. European Journal of control, 2004, 10(5): 432-450. |
| [5] | Ruiter D E, Anton H J. Some applications of passivity-based control and invariance principles[J]. IET Control Theory & Applications, 2013, 7(7): 1039-1048. |
| [6] | Lanzon A, Petersen I R. Stability robustness of a feedback interconnection of systems with negative imaginary frequency response[J]. IEEE Transactions on Automatic Control, 2008, 53(4): 1042-1046. |
| [7] | Petersen I R. Physical interpretations of negative imaginary systems theory[EB/OL]. [2015-03-04]. http://arxiv.org/abs/1503.01189. |
| [8] | Sourav P, Lanzon A. Stability analysis of interconnected systems with “mixed” negative-imaginary and small-gain properties[J]. IEEE Transactions on Automatic Control, 2011, 56(6): 1395-1400. |
| [9] | Cai C, Hagen G. Stability analysis for a string of coupled stable subsystems with negative imaginary frequency response[J]. IEEE Transactions on Automatic Control, 2010, 55(8): 1958-1963. |
| [10] | Wang J, Han Q L, Yang F. Event-based stability and passivity of negative feedback interconnected mechanical systems in network environments[C]//2012 2nd Australian Control Conference (AUCC). Piscataway, NJ, USA: IEEE, 2012: 104-109. |
| [11] | Bharath B, Moheimani S O R, Petersen I R. A negative imaginary approach to modeling and control of a collocated structure[J]. IEEE/ASME Transactions on Mechatronics, 2012, 17(4): 717-727. |
| [12] | Sajal D K, Hemanshu R P, Petersen I R. Resonant controller design for a piezoelectric tube scanner: A mixed negative-imaginary and small-gain approach[J]. IEEE Transactions on Control Systems Technology, 2014, 22(5): 1899-1906. |
| [13] | Opmeer M. Infinite-dimensional negative imaginary systems[J]. IEEE Transactions on Automatic Control, 2011, 56(12): 2973-2976. |
| [14] | Mabrok M A, Kallapur A G, Petersen I R, et al. Generalized negative imaginary lemma for descriptor systems[J]. Journal of Mechanics Engineering and Automation, 2012, 2(1): 17-21. |
| [15] | Iwasaki T, Hara S. Generalized KYP lemma: Unified frequency domain inequalities with design applications[J]. IEEE Transactions on Automatic Control, 2005, 50(1): 41-59. |
| [16] | Iwasaki T, Hara S, Fradkov A L. Time domain interpretations of frequency domain inequalities on (semi) finite ranges[J]. Systems & Control Letters, 2005, 54(7): 681-691. |
| [17] | Fradkov A. Conic S-procedure and constrained dissipativity for linear systems[J]. International Journal of Robust and Nonlinear Control, 2007, 17(5/6): 405-413. |
| [18] | Kojima C, Hara S. Controller synthesis for multiple finite frequency specifications: Dissipation inequalitiesapproach[C]//Proceedings of 2010 SICE Annual Conference. Piscataway, NJ, USA: IEEE, 2010: 173-178. |
| [19] | Xiong J, Petersen I R, Lanzon A. Finite frequency negative imaginary systems[J]. IEEE Transactions on Automatic Control, 2012, 57(11): 2917-2922. |
| [20] | Liu M, Xiong J. On α-and D-negative imaginary systems[J]. International Journal of Control, 2015(3): 1-15. |
| [21] | Gu K, Chen J, Kharitonov V L. Stability of time-delay systems[M]. Boston, MA, USA: Birkhäuser, 2003: 213-217. |
| [22] | 张冬梅, 俞立. 线性时滞系统稳定性分析综述[J]. 控制与决策, 2008, 23(8): 841-849. Zhang D M, Yu L. Survey on the stability analysis of linear time-delay systems[J]. Control and Decision, 2008, 23(8): 841-849. |
| [23] | Zhang X N, Yang G H. Performance analysis for multi-delay systems in finite frequency domains[J]. International Journal of Robust and Nonlinear Control, 2012, 22(8): 933-944. |
| [24] | Niculescu S I, Lozano R. On the passivity of linear delay systems[J]. IEEE Transactions on Automatic Control, 2001, 46(3): 460-464. |
| [25] | Fridman E, Shaked U. On delay-dependent passivity[J]. IEEE Transactions on Automatic Control, 2002, 47(4): 664-669. |
| [26] | Fridman E, Shaked U. New bounded real lemma representations for time-delay systems and their applications[J]. IEEE Transactions on Automatic Control, 2001, 46(12): 1973-1979. |
| [27] | Lu G, Daniel W C H, Yeung L F. Strict positive realness for linear time-delay systems[J]. International Journal of Systems Science, 2003, 34(1): 1-9. |
| [28] | Mahmoud M S, Abdulla I. Passivity and passification of time-delay systems[J]. Journal of Mathematical Analysis and Applications, 2004, 292(1): 247-258. |
| [29] | Mahmoud M S, Xia Y. A generalized approach to stabilization of linear interconnected time-delay systems[J]. Asian Journal of Control, 2012, 14(6): 1539-1552. |
| [30] | Chen N, Liu Y, Liu B, et al. Parametric absolute stabilization for interconnected Lurie time-delay systems with polytopicuncertainty[J]. Asian Journal of Control, 2014, 16(1): 225-232. |
| [31] | 张先明, 吴敏. 线性时滞系统的时滞相关无源控制[J]. 控制理论与应用, 2015, 22(3): 391-394. Zhang X M, Wu M. Delay-dependent passive control for linear system with delay[J]. Control Theory & Applications, 2015, 22(3): 391-394. |
| [32] | Wu Z, Park J H, Su H, et al. Dissipativity analysis for singular systems with time-varying delays[J]. Applied Mathematics and Computation, 2011, 218(8): 4605-4613. |
| [33] | 陈云, 薛安克, 王俊宏. 随机时滞系统的时滞相关无源控制[J]. 自动化学报, 2009, 35(3): 324-327. Chen Y, Xue A K, Wang J H. Delay-dependent passive control of stochastic delay systems[J]. Aata Automatica Sinica, 2009, 35(3): 324-327. |
| [34] | Zhang B, Zheng W X, Xu S. Passivity analysis and passive control of fuzzy systems with time-varying delays[J]. Fuzzy Sets and Systems, 2011, 174(1): 83-98. |
| [35] | Tseng W, Liu C N, Chauchin S U. Passive reduced-order macro-modeling for linear time-delay interconnect systems[J]. IEICE Transactions on Electronics, 2006, 89(11): 1713-1718. |
| [36] | Nikhil C. Passivity results for interconnected systems with time delay[C]//Proceeding of 47th IEEE Conference on Decision and Control. Piscataway, NJ, USA: IEEE, 2008: 4620-4625. |
| [37] | Mabrok M A. Kallapur A G, Petersen I R, et al. Spectral conditions for negative imaginary systems with applications to nanopositioning[J]. IEEE/ASME Transactions on Mechatronics, 2014, 19(3): 895-903. |
| [38] | Sipahi R, Olgac N. Active vibration suppression with time delayed feedback[J]. Journal of Vibration and Acoustics, 2003, 125(3): 384-388. |
| [39] | 张宝琳, 张宇. 海洋平台振动系统的时滞依赖滑模H∞控制方法[J]. 信息与控制, 2014, 43(6): 727-734. Zhang B L, Zhang Y. Delay dependent sliding model H∞ control for the vibration system of offshore platforms[J]. Information and Control, 2014, 43(6): 727-734. |
| [40] | 陈强, 栾小丽, 刘飞. 高维多变量时滞系统多环PI控制的解析设计[J]. 信息与控制, 2014, 43(2): 205-210. Chen Q, Luan X L, Liu F. Analytical design of multiloop PI control for high-dimensional multivariable systems with time-delay[J]. Information and Control, 2014, 43(2): 205-210. |
| [41] | 惠俊军, 张合新, 周鑫, 等. 含非线性扰动的区间变时滞系统鲁棒稳定新判据[J]. 信息与控制, 2014, 43(5): 529-533. Hui J J, Zhang H X, Zhou X, et al. New robust stability criteria for interval time-varying delay systems with nonlinear perturbations[J]. Information and Control, 2014, 43(5): 529-533. |



