2. 吉林大学通信工程学院, 吉林 长春 130022
2. Department of Control Science and Engineering, Jilin University, Changchun 130022, China
1 引言
随着汽车工业技术的迅猛发展,关乎车辆行驶安全的汽车操纵稳定性日益受到人们的关注. 四轮转向(four wheel steering,4WS)是一种有效改善车辆操纵稳定性的主动底盘控制技术. 4WS汽车后轮可以主动参与转向,从而可以提高汽车的瞬态响应能力. 4WS技术不仅可以减小车辆质心侧偏角,还可以增加轮胎侧向力裕度,对于轨迹保持和稳定性控制有易于实现的优势,对提高汽车主动安全性有着重要的深远意义[1, 2].
随着4WS控制技术的不断进步及研究的不断深入和控制性能的不断提升,人们希望4WS汽车可以抵御汽车参数变化的影响,并可以保持驾驶员所期望的转向特性. 为提高汽车的转向控制能力,已经有许多控制方法被应用于4WS控制,如PID控制[3, 4]、 鲁棒控制[5, 6, 7]、 滑模控制[8, 9, 10]、 神经网络控制[11, 12]等. 然而,这些控制方法大多只是针对后轮转向控制的. 因为仅将后轮转角作为唯一的控制量,被控量一般是汽车质心侧偏角或者横摆角速度,只能改善汽车的部分操纵性能. 近年来,线控转向(steering by wire,SBW)技术得到快速发展,线控操纵车辆的前、 后轮可以同时作为主动控制输入[13]. 这使得基于模型跟踪的控制策略成为可能,进而可以保证被控汽车同时具有驾驶员期望的理想侧偏角和横摆角速度[14].
为了更有效地提高车辆的操纵性,本文即采用了这种前、 后轮主动转向相结合的控制策略. 一般而言,轨迹保持可以用车辆的侧偏角来描述,而稳定性问题可以由横摆角速度来描述. 因此,选取车辆质心侧偏角和横摆角速度作为4WS控制系统的控制变量. 本文以模型跟踪控制策略为基础,将前馈控制与反馈控制相结合,以实现实际车辆模型对参考模型的状态跟踪. 其中前馈控制器是依据线性2自由度车辆模型推导得到的. 为了提高4WS车辆抵御外界干扰的能力,并且将执行机构输出阈值的限制考虑进来,本文提出了一种约束H∞输出反馈控制器,将其作为4WS系统的反馈控制器. 此外,给出了约束H∞输出反馈控制器的设计方法和求解步骤. 最后,进行了仿真实验以验证所设计控制器的有效性.
2 2自由度车辆模型汽车的四轮主动转向控制与质心侧偏角和横摆角速度的关系最为密切,它们可以从不同方面来表征车辆的操纵稳定性. 为了便于研究,本文选择线性2自由度车辆模型作为车辆操纵稳定性控制算法研究模型. 理论和实验都证明,在正常车速范围的非紧急状态和小转向角的情况下,2自由度模型能以较高的精度表征车辆转向的实际物理过程,基于该模型设计的控制器能够正常工作[1]. 为了便于分析,需要作如下假设:
·忽略转向系统的影响,直接以前、 后车轮转角作为输入;
·忽略悬架的作用,认为汽车只做平行于地面的平动;
·假设汽车侧向加速度小于0.4 g,车轮转角5°,轮胎侧偏特性处于线性范围内且左右车轮特性相同;
·忽略空气阻力作用.
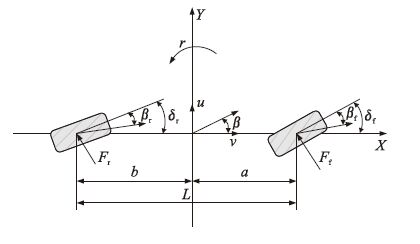
基于以上假设,可以得到只具有侧向运动和横摆运动的2自由度车辆模型,如图 1所示. 建立车辆坐标系,原点位于汽车的质心,车辆前进的方向为x轴正方向,水平向左为y轴正方向,z轴正方向用右手螺旋定则确定. 根据牛顿第二定律,可以得到2自由度车辆模型的动力学方程为


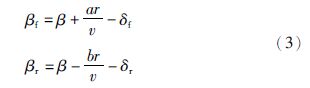

|
| 图 1 2自由度车辆模型 Fig. 1 2-degree-freedom vehicle model |
将式(4)写成标准状态空间形式:


考虑侧向风引起的外部干扰,式(1)可重写成:


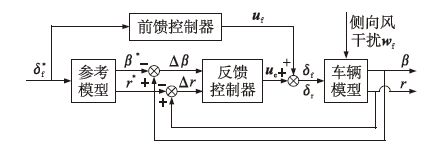
4WS控制系统可以通过对汽车的侧向运动和横摆运动进行控制,实现汽车运动轨迹保持和车身姿态的控制,进而提高汽车的操纵稳定性和主动安全性. 此外,当遭遇外界干扰(如侧向风)时,4WS系统能主动控制车轮转角,调节各个车轮的轮胎力,使汽车具有较好的主动安全性和抗干扰能力. 本文将前轮转角和后轮转角同时选做主动控制输入,采用基于模型跟踪的控制策略以保证被控车辆同时具有驾驶员期望的理想侧偏角和横摆角速度,整个系统的控制方案如图 2所示. 由图 2可以看出,δf*为将驾驶员输入的方向盘转角经过转换后得到前轮转角输入. 参考模型给定理想的质心侧偏角和横摆角速度,理想横摆角速度与车辆实际的横摆角速度之差及理想质心侧偏角与车辆实际质心侧偏角之差作为反馈控制器的输入. 反馈控制器的作用是尽量减少实际车辆与参考模型的状态偏差,与前馈控制器共同决策出所需的前轮转角和后轮转角,以完成转向过程的横摆率跟踪任务,同时尽量减少车辆质心侧偏角,以保持车身良好姿态. 前馈控制器是根据理想参考模型的给定逆推得到的. 兼顾执行机构输出饱和与外界干扰的影响,反馈控制器采用约束H∞输出反馈控制方法. 整体控制输入u由前馈控制输入uf和反馈控制输入ue构成:

|
| 图 2 4WS系统框图 Fig. 2 Block diagram of 4WS system |
在汽车的质心侧偏角较小的情况下,由线性2自由度车辆模型决定的横摆角速度对汽车来说是最稳定的,因此可以将线性2自由度车辆模型的转向特性作为理想的转向特性. 根据汽车理论,可构造汽车的理想横摆角速度为[16]
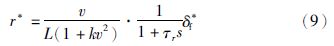



前馈控制器的作用是给定前后轮转角输入的工作点,使4WS系统处于小偏差调节状态. 采用线性2自由度车辆模型(5),对其进行拉普拉斯变换,得到相应的传递函数矩阵:

设计前馈控制器Cf(s),在理想条件下使得2自由度车辆模型的动态响应与车辆参考模型的理想动态响应一致,即驾驶员给定的前轮转角输入,经过前馈控制器和车辆模型后可以得到理想的质心侧偏角和横摆角速度,则应当满足如下关系式:
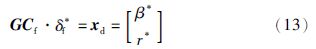
将式(9)、 (10)、 (12)代入式(13),求解等式(13),可得到前后轮主动转向前馈控制规律为


为了提高4WS系统的抗干扰能力,反馈控制采用约束H∞输出反馈控制,定义如下的状态误差变量:

由式(7)和式(11)可得

根据式(13)和式(15)可知:

将式(12)代入式(18),并且进行拉普拉斯逆变换可以得到

将式(19)、 (11)代入式(17),可以将式(17)后两项消去,进而得到误差跟踪状态方程的简化形式:

反馈控制器的设计目的是希望在转向过程中,实际车辆模型的输出能够跟踪理想车辆模型的输出,以保证二者状态跟踪误差为最小. 因此将实际车辆模型与理想车辆模型的状态偏差作为性能输出:

考虑到执行机构输出阈值的限制,前后轮转角控制输入不能超过允许的最大值,即:

因此将前后轮转角输入作为约束输出:

综上所述,该控制策略的目标是找到一个稳定的H∞输出反馈控制器,满足如下条件:
(1) 最小化性能输出z1,使汽车可以跟踪上参考模型的质心侧偏角β*和横摆角速度r*,以提高汽车的跟踪性能和操纵稳定性;
(2) 限定约束输出z2中的各个变量在允许范围内,以满足4WS系统的时域硬约束.
3.5 约束H∞输出反馈控制器的求解本节依据线性矩阵不等式(linear matrix inequality,LMI),将对前述约束H∞输出反馈控制律进行讨论,并给出具体的求解方案. 不失一般性,将被控系统重写成如下一般的状态空间形式:
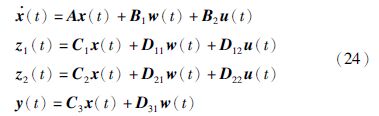
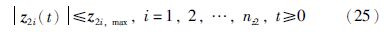
(1) (A,B2,C3)是可稳定的和可检测的;
(2) 干扰输入w∈Rnw是未知的,但必须是能量有界的,并且属于如下集合:

考虑具有如下形式的输出反馈控制率K:
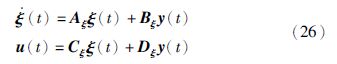


基于LMI方法,可以推导得到求解约束H∞输出反馈控制器的半定规划问题:


假如得到了上述LMI优化问题的一组最优解(γ*,X*,Y*,$\hat A$*,$\hat B$*,$\hat C$*,$\hat D$*),构建控制器K步骤为: 通过奇异值分解得到满足等式MNT=I-XY的满秩矩阵M和N. 控制器参数可通过式(29)获得:

采用类似文[18]方法可证明: 依据式(29)所设计的输出反馈控制器K保证闭环系统是内部稳定的,从w(t)到z1(t)的H∞范数最小,能够满足相应的时域硬约束条件.
4 仿真结果与分析为了验证基于约束H∞输出反馈控制器的四轮转向系统的有效性,利用Matlab/Simlink进行了相关的动力学仿真实验,所采用的车辆参数如表 1所示. 为了对比控制效果,同时进行了同结构参数的前轮转向FWS汽车和经典的比例控制4WS控制仿真实验. 比例控制前、 后轮转角的关系为[19]

| 模型参数 | 数值 |
| 整车质量m | 1 359.8 kg |
| 汽车质心到前轴距离a | 1.063 m |
| 汽车质心到后轴距离b | 1.485 m |
| 横摆转动惯量Iz | 1 992.54 kg/m2 |
| 前轮侧偏刚度kf | 52 480 N/rad |
| 后轮侧偏刚度kr | 88 416 N/rad |
汽车方向盘角阶跃响应是评价汽车操纵稳定性的一个基本实验,本文分别在低速和高速两种情况下进行了方向盘角阶跃实验. 首先采用v=36 km/h较低行驶车速,前轮转角输入为4°(0.069 8 rad)的角阶跃输入,起跃时间1 s,总仿真时间为5 s.
由图 3仿真结果可以看出,H∞控制的4WS汽车和比例控制4WS汽车的质心侧偏角稳态值都接近零值,相对于传统前轮转向FWS汽车稳态值0.017 3 rad减少了很多. 但是,比例控制4WS汽车在1 s~1.5 s之间有明显的瞬态振荡和超调,无振荡超调的H∞控制的4WS汽车体现出了明显优势. 对于横摆角速度,H∞控制的4WS汽车的横摆角速度稳定值接近于传统前轮转向FWS汽车,这可以保证驾驶员的驾驶感觉不会发生较大的变化. 而比例控制4WS汽车横摆角速度稳定值相对于传统前轮转向FWS汽车有明显上升,会导致驾驶员少打方向盘.

|
| 图 3 方向盘角阶跃响应曲线(v=36 km/h) Fig. 3 The step response of steering angle (v=36 km/h) |
下面采用v=108 km/h较高行驶车速,其它仿真条件与上一组仿真实验相同. 由图 4仿真结果可以看出,H∞控制的4WS汽车质心侧偏角稳态值接近零值,调节时间很短且无瞬态振荡和超调; 同时,H∞控制的4WS汽车横摆角速度稳定值也几乎与传统前轮转向FWS汽车保持一致,并且没有传统前轮转向FWS汽车的瞬态振荡和超调. 由此可以看出,无论低速还是高速,H∞控制的4WS汽车的瞬态过度过程都很平稳,没有振荡和超调,提供驾驶员熟悉的驾驶感觉,可以保证汽车的平稳转向.

|
| 图 4 方向盘角阶跃响应曲线(v=108 km/h) Fig. 4 The step response of steering angle (v=108 km/h) |
为了进一步验证H∞控制器的控制效果,又进行了附加外部干扰的方向盘正弦输入仿真实验. 仿真给定的前轮转角输入为如图 5所示的正弦输入,采用的车速为v=108 km/h. 为了将外部干扰(如侧向风干扰)考虑进来,在仿真时间2 s~4 s之间给定汽车的一个幅值为0.2的脉冲干扰输入,如图 6所示.

|
| 图 5 驾驶员转向输入 Fig. 5 Front wheel angle input |

|
| 图 6 侧向风干扰输入 Fig. 6 Side wind disturbance input |
由图 7的仿真结果可以看出,在0~2 s之间,H∞控制的4WS汽车的质心侧偏角始终保持接近于0,其横摆角速度也都很好地跟踪了前轮转向FWS汽车的横摆角速度. 比例控制4WS汽车也可以将质心侧偏角保持在较小值,而其横摆角速度要小于前轮转向FWS汽车,因而改变了驾驶员的驾驶感觉与操作强度. 在2 s~4 s之间,由于外部干扰的影响,比例控制4WS汽车和前轮转向控制FWS汽车都产生不合理的质心侧偏角和横摆角速度,使车辆不能保持良好的跟踪性能,影响汽车操纵稳定性. 而对比而言,在此时段,4WS汽车仍然可以保持很小的质心侧偏角和良好的操纵稳定性,对侧向风的抗干扰能力具有明显优势. 同时,由图 8可以看出,4WS汽车的执行机构输出,即前、 后轮转角控制输入均限定在合理范围内.

|
| 图 7 方向盘角正弦输入响应 Fig. 7 The sine input response of steering angle |

|
| 图 8 前、 后轮转角约束输出曲线 Fig. 8 The constrained output of front and rear wheels |
本文以约束H∞控制方法为基础,依据模型跟踪控制策略,设计4WS前馈控制器和反馈控制器. 在保证车辆质心侧偏角为零的前提下,同时可以使横摆加速度实时跟踪上理想的横摆角速度. 在相同车辆参数配置及相同工况条件下,将约束H∞控制的4WS车辆与比例控制4WS车辆和FWS车辆进行了仿真实验对比. 通过仿真实验验证了约束H∞控制方法可以有效提高汽车的操纵稳定性,并且在抑制外界干扰的能力方面具有明显的优势. 但是,由于受限于目前的硬件环境,本文所提出的方法还停留在软件仿真验证阶段,将来如果有条件进行实车实验,相信将会得到许多更有价值的结果.
| [1] | 郭孔辉. 汽车操纵动力学[M]. 长春: 吉林科学技术出版社, 1991. Guo K H. Vehicle handling dynamics[M]. Changchun: Jilin Science and Technology Press, 1991. |
| [2] | Nagai M. Perspectives of research for enhancing active safety based on advanced control technology[J]. Vehicle System Dynamics, 2007, 45(5): 413-431. |
| [3] | Qi Z J, Yang Z G, Huang Y. Lane change track control for intelligent 4WS vehicle based on fuzzy adaptive PID[J]. Chinese Journal of Automotive Engineering, 2012, 2(5): 379-384. |
| [4] | Yu J B, Han Z N. Fuzzy PID control for 4WS vehicle based on model tracking technology[J]. Journal of Chinese Agricultural Mechanization, 2013, 34(4): 188-192. |
| [5] | Yin G D, Chen N, Wang J X, et al. Robust control for 4WS vehicles considering a varying tire-road friction coefficient[J]. International Journal of Automotive Technology, 2010, 11(1): 33-40. |
| [6] | Yin G D, Chen N, Li P. Improving handling stability performance of four-wheel steering vehicle via μ-synthesis robust control[J]. IEEE Transactions on Vehicular Technology, 2007, 56(5): 2432-2439. |
| [7] | Shu M, Chen C, Liu R, et al. A robust control approach for the steering and traction of autonomous 4WS vehicles[C]//International Conference on Control Engineering and Electronics Engineering. 2014: 13. |
| [8] | Zhou Q, Wang F, Li L. Robust sliding mode control of 4WS vehicles for automatic path tracking[C]//Proceedings of 2005 Intelligent Vehicles Symposium. Piscataway, NJ, USA: IEEE, 2005: 819-826. |
| [9] | Alfi A, Farrokhi M. Hybrid state-feedback sliding-mode controller using fuzzy logic for four-wheel-steering vehicles[J]. Vehicle System Dynamics, 2009, 47(3): 265-284. |
| [10] | Kazemi M, Shirazi K H. Handling enhancement of a sliding-mode control assisted four-wheel steer vehicle[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2012, 226(2): 234-246. |
| [11] | Zhou L, Wang C, Ou L L. Research on four-wheel steering vehicle control based on fuzzy control[J]. Machinery & Electronics, 2009(3): 40-42. |
| [12] | Murat D, Metin G. Adaptive optimal control allocation using Lagrangian neural networks for stability control of a 4WS/4WD electric vehicle[J]. Transactions of the Institute of Measurement and Control, 2013, 35(8): 1139-1151. |
| [13] | 包凡彪. 汽车线控转向系统及关键技术[J]. 汽车运用, 2009(3): 27-29. Bao F B. The electric power steering systems and its key technology[J]. Auto Application, 2009(3): 27-29. |
| [14] | 李彬, 喻凡. 四轮主动转向的模型跟踪控制[J]. 上海交通大学学报, 2009(10): 1531-1535. Li B, Yu F. Model following control of four-wheel active steering vehicle[J]. Journal of Shanghai Jiaotong University, 2009(10): 1531-1535. |
| [15] | You S S, Chai Y H. Multi-objective control synthesis: An application to 4WS passenger vehicles[J]. Mechatronics, 1999, 9(4): 363-390. |
| [16] | Nagai M, Hirano Y, Yamanaka S. Integrated control of active rear wheel steering and direct yaw moment control[J]. Vehicle System Dynamics, 1997, 27(5/6): 357-370. |
| [17] | Chen H, Sun P Y, Guo K H. A multi-objective control design for active suspensions with hard constraints[C]//Proceedings of the 2003 American Control Conference. Piscataway, NJ, USA: IEEE, 2003: 4371-4376. |
| [18] | Yu S Y, Wang J, Chen H. Output feedback H∞ control of constrained linear systems[C]// 2015 10th Asian IEEE Control Conference. Piscataway, NJ, USA: IEEE, 2015: 1-6. |
| [19] | 安部正人. 汽车运动和操纵[M]. 北京: 机械工业出版社, 1998. Abe M. Vehicle motion and handling[M]. Beijing: China Machine Press, 1998. |



